Математическая модель и экспериментальные исследования поведения вязкоупругих наполненных полимеров при двухчастотных воздействиях
Автор: Янкин А.С., Бульбович Р.В., Словиков С.В.
Статья в выпуске: 2, 2017 года.
Бесплатный доступ
В настоящее время высоконаполненные полимерные композиты широко используются в ответственных конструкциях аэрокосмической техники и других отраслях. Данные конструкции в процессе эксплуатации испытывают сложные гармонические нагрузки. В связи с этим актуально развитие методов экспериментального исследования и определения деформационных свойств высоконаполненных полимерных композитов, а также методов расчета конструкций, работающих в экстремальных условиях. Рассмотрены линейные и нелинейные интегральные операторы для описания механического поведения вязкоупругих материалов. На основе общей формы записи физически нелинейных операторов вязкоупругих сред (интегральный ряд Вольтерра-Фреше) представлена нелинейная математическая модель на основе комплексных параметров, описывающая поведение вязкоупругого материала в условиях действия разнообразных стационарных одночастотных и двухчастотных нагрузок (при любом соотношении частот и амплитуд). Проведены анализ представленной математической модели, а также ее сопоставление с предложенной ранее моделью с допущениями о линейной зависимости вязкоупругих параметров от амплитуд деформации, отсутствии искажений петли гистерезиса (искажений гармоник) при деформировании. Предложено использовать полиномиальные зависимости для описания зависимостей вязкоупругих параметров от различных условий нагружения (с использованием температурно-временной аналогии). Для определения полиномиальных зависимостей были проведены двухчастотные экспериментальные исследования. После обработки экспериментальных данных были выявлены зависимости вязкоупругих параметров от частот нагружения и температуры. Полученные результаты позволяют разработать оптимальный план экспериментальных исследований, идентифицировать предложенную параметрическую модель, оценить влияние различных вязкоупругих параметров на точность описания поведения материала при сложных гармонических воздействиях.
Высоконаполненные полимерные композиты (эластомеры), двухчастотное нагружение, комплексный динамический модуль, угол потерь, динамические механические свойства (анализ), интегральный ряд вольтерра-фреше
Короткий адрес: https://sciup.org/146211675
IDR: 146211675 | УДК: 534-16 | DOI: 10.15593/perm.mech/2017.2.12
Текст научной статьи Математическая модель и экспериментальные исследования поведения вязкоупругих наполненных полимеров при двухчастотных воздействиях
PNRPU MECHANICS BULLETIN
Актуальность темы обусловлена использованием высоконаполненных полимерных композитов в ответственных конструкциях аэрокосмической техники и других отраслях [1–3]; действием сложных гармонических нагрузок на подобные конструкции вследствие всевозможных ударных воздействий, транспортировки, пульсаций внутрикамерного давления и т.д. [4, 5]; необходимостью развития методов экспериментального исследования и определения деформационных свойств материалов, а также методов расчета конструкций, работающих в экстремальных условиях.
В целом работа направлена на разработку методик проведения динамического опыта, определение вязкоупругих параметров высоконаполненных полимерных композитов при стационарных двухчастотных воздействиях и процедуры идентификации используемой многофакторной математической модели для оценки напряженно-деформированного состояния вязкоупругих конструкций аэрокосмической техники.
1. Математическая модель описания поведения вязкоупругих материалов при стационарных двухчастотных нагрузках
Одним из наиболее универсальных для описания линейных вязкоупругих свойств является способ, основанный на применении линейных интегральных уравнений Больцма-на–Вольтерра [6, 7]. В случае одноосного растяжения-сжатия можно записать
g( t)= j E(t-t) dS(l) dт, -to ^T где τ – время, предшествующее моменту времени наблюдения t; Е(t) – функция релаксации (ядро релаксации). Бесконечный нижний предел интегрирования подразумевает учет полной истории деформирования.
На практике бывают случаи, когда вязкоупругие конструкции работают в условиях стационарных гармонических колебаний. Описанные выше соотношения между напряжениями и деформациями применимы и при таких условиях эксплуатации. Однако при описании поведения вязкоупругого материала удобнее использовать комплексные параметры [5–8].
Пусть далее деформации от времени изменяется по гармоническому закону вида
8 ( t ) = 8 a • em t ,
где ε а – амплитуда деформации; ω – угловая частота. Подставим (2) в (1), в результате получим
t
g( t) = ims a j E (t -t) eimT d т.
-to
Путем замены переменной t – τ = η (3) можно записать в виде
o(t) = -imsa • eimt jE (n) edn .
to
Воспользуемся формулой Эйлера [9]
e i m ( n ) = cos Wn- i sin mn
и перепишем (4) в форме
G ( t ) = 8 а • e™ t
m j E (n) sin mn d n + i m j E (n) c° s Ю П d П
to
to
.
Далее будем рассматривать такие ядра релаксации, для которых интегралы из уравнения (6) сходятся (например, экспоненциальное ядро E ( n ) = Ae — en при в > 0). Таким образом, ограничения, накладываемые на ядра, фактически сводятся к тому, что все полученные уравнения будут справедливы для асимптотически затухающей модели вязкоупругого деформирования при о = const.
Примем to
E' = mj E (n) sin mn dn, to
E" = m j E (n) cos mn d n,
E = E' + iE" , (7)
E' = E cos ф E , (8)
E" = E * sin ф E ,
E* = VE'2 + E''2 , tan ф E
E''
E ’
где E - комплексный параметр; Е' - действительная часть комплексного параметра; Е" -мнимая часть комплексного параметра, ф E ; E - вязкоупругие параметры.
Таким образом, (6) можно записать в виде
^(t) = E -8a • с"'t.(10)
Подставив (8) и (9) в (7) и, воспользовавшись формулой Эйлера, получим
E = E * e^ E.(11)
Затем перепишем (10) с учетом (11):
о( t) = 8 aE * ei(m t+ф E).(12)
Интерпретация (12) важна с физической точки зрения. При стационарных гармонических колебаниях деформация запаздывает от напряжения на величину, определяемую углом потерь ф E [7].
Наполненным полимерам свойственно нелинейное поведение: отличие петли гистерезиса от эллиптической формы [6, 10], размягчение материала (эффект Маллин-за-Патрикеева) [11, 12], влияние амплитуды деформации (эффект Пэйна) [12, 13] и предварительной статической деформации на определяемые вязкоупругие характеристики [14-16].
Общее описание нелинейной математической модели вязкоупругого поведения материала было получено Вольтерра с использованием представления, разработанного Фреше. Уравнение Вольтерра-Фреше [8, 17, 18] является общей формой записи физически нелинейных операторов вязкоупругой среды. Для одного измерения его можно записать в следующем виде:
ttt
с ( t ) = J E 1 ( t -т 1 ) d 8(т 1 ) + J J E 2 ( t -т 1 ; t -т2 ) d 8(т 1 ) d 8(т2) +
-∞-∞ -∞ ttt
+ J J J E3 (t-T1;t-t2;t-t3)d8(т1)d8(t2)d8(t3) +... +
-∞ -∞ -∞ tt
+ J ... J En ( t -T 1 ;...; t -T n ) d 8 ( т 1 )... d 8 ( t n ) + ...
-∞-∞
Вследствие того что зависимости вязкоупругих параметров от предварительной статической деформации для данного типа материалов с достаточной точностью описываются полиномами второй степени [19], в дальнейшем будем ограничиваться только первыми тремя членами ряда (13).
В случае действия стационарных двухчастотных колебаний деформации от времени изменяются по гармоническому закону вида
E ( t ) = £ a ! • e
i to ! t
, _ i to-, t
+ £ a 2 • e 2 , где индекс 1 соответствует низкочастотной гармонике; индекс 2 - высокочастотной гармонике.
Проделаем действия, аналогичные тем, которые были сделаны ранее (2)-(5). В результате всех преобразований получим
п ( t ) = г а i e i to i *Ет ( to i ; T ) + £ ^ , e i 2 to 1 t E 2Л ( to ; T ) + £ 3 a , e i 3 to i t E .„ ( to ; T ) + +£ a 1 e to t £ a 2 e i to 2 t E .,. ( to i ; to 2; T ) + £ 2, e t £ a 2 e i to 2 ‘E^ ( to i ; to 2; T ) + +£ a i e i to | t £га 2 e tE^4 ( to i ; to 2; T ) + £ o 2 ei to 2 *ЕШ ( to 2; T ) +
+£a 2 e tE2/2 (to2; T) + £ 2 e tV. (to.; T), да
Em(toi;T) = toi J Ei(4i)sin toi ni dni, да
E"i(toV; T) = toi J Ei(nDcos toi ni dni,
Еш^; T) = Е^; T) + iE^; T),(i8)
да
E'/2(to2; T) = to2 J Ei (ni)sin toto dni, да
E"2 (to2; T) = to2 J Ei (ni) cos to2ni dni,(20)
Ei/2(to2; T) = E'2(to2; T) + iE">2; T),(2i)
да да
E2/i ( to i ; T ) = -to 2 J J E 2( n i ; n 2 ) cos( to i n i + to n 2 ) d n i d n 2 , 0 0
да да
E " i ( to i ; T ) = to 2 J J E 2 ( n i ; n 2 ) sin( to n i + to n 2 ) d n i d n 2 , 0 0
E 2/i ( to i ; T ) = E' i ( to i ; T ) + iE" ( to i ; T ),
E 2'^2; T ) = -to 2 J J
да да
E 2 (n i ; n 2 )cos(to 2 n i +to 2 n 2 ) d n i d n 2 ,
0 0
да да
E " /2 (to 2 ; T ) = to 2 J J E 2 (n i ; n 2 ) sin^n + to 2 n 2 ) d n i d n 2 ,
0 0
E 2/2 ( to 2; T ) = E ' 2 ( to 2 ; T ) + iE" 2 ( to 2; T ),
да да
E 2/з (to i ; to 2 ; T ) = -to i to 2 J J E 2 (n i ; n) [cos(to i n i + to 2 n) + cos^n + to i n)] d n i d n, (28) 0 0 да да
E "/3( to i; to2; T ) = toi to2 J J E 2(ni; n2) [sin(toi ni +to2n2) + sin(to2ni +toi n2)] d ni d n2 (29)
0 0
Е2/3 (“; м2; T) = Е'/з (“; м2; T) + iE"3 (“; м2; T), да да да
Eз /1 (® 1 ; T ) = “ з J J J E з (П т ; п 2 ; П з ) sin( “ 1 п +м n + “ 1 П з ) d п d n d П з ,
0 0 0
да да да
E" /1 (М 1 ; T ) =-“ JJJ E з (П 1 ; П 2 ; П з )cos(“ 1 П 1 + “ 1 П 2 + “ 1 П з ) d П 1 d П 2 d П з , 0 0 0 '
Eз/1 (“1;T) = Ез/1 (м1;T)+iEз/1 (м1;T), да да да
E' /2 (^ 2 ; T ) = -“ 2 J J J E з (П 1 ; П; П з ) sin(“ 2 П 1 + “ 2 П 2 + ^П з ) d П 1 d П 2 d П з ,
0 0 0
да да да
E" 2 (“ 2 ; T ) = м 2 J J J E з (П 1 ; П 2 ; П з ) cos^n + “ 2 П 2 + “ 2 П) d П 1 d П 2 d П з , 0 0 0
Eз/2 (“2; T) = E'2 (“2; T) + iE^ (м2; T), да да да
E з ' /з ( “ ; “ 2 ; T ) = -“(“ J J J Е з ( П 1 ; П 2 ; П з ) [ sin^ n + “ 1 П 2 + “ 1 П з ) +
0 0 0
+ sin(“1 П1 + “2п2 + “ Пз) + sin(“1 п1 + “1 П2 + “2Пз)] d П d П2 d Пз,
да да да
E" ( “ 1 ; “ 2 ; T ) = -m 2 м . J J J Е з ( П 1 ; П 2 ; П з ) [ cos^ ^ + “ 1 П 2 + “ 1 П з ) + 0 0 0
+ cos( “ 1 П 1 + “ 2 п 2 + “ 1 П з) + cos( “ 1 П 1 +“ 1 П 2 + “ 2 П з) ] d П 1 d П 2 d П з,
Ез/з (м1; м2; T) = E^ (“1; м2; T) + iEз 'з (“; м2; T), да да да
E' /4 ( “ 1 ; “ 2 ; T ) = -м 1 “ 2 JJ J E з ( П 1 ; п 2 ; П з ) [ sin( “ 1 П 1
+ “ 2 П 2 +“ 2 П з) +
0 0 0
+ sin(“2n1 +“1 П2 +“2Пз) + sin(“2n1 +“2п2 +“1 Пз) |dП1 dП2dпз, да да да
E" 4 ( “ 1 ; “ 2 ; T ) = -“ 1 “ 2 J J J E з ( П 1 ; П 2 ; П з ) [ cos( “ 1 П 1 + “ 2 П 2 + “ 2 П ) + 0 0 0
+ cos( “ 2 n 1 +“ 1 П 2 +“ 2 П з) + cos( “ 2 n 1 +“ 2 п 2 +“ 1 П з) ] d П 1 d П 2 d П з,
Ёз/4 ( м 1; м 2; T ) = E' /4 ( м 1; м 2; T ) + iE" 4 ( м 1; м 2; T ).
(з0)
(з1)
(з2)
(зз)
(з4)
(з5)
(зб)
(з?)
(з8)
(з9)
* т-**
Анализ (15)-(42) показывает, что E 1/1( “ 1; T ) и E 1/2( “ 2; T ), E 1/1( “ 1; T ) и E 1/2( “ 2; T ),
9 E 1/1 ( “ 1 ; T ) и Ф E 1/2 ( “ 2 ; T ), E 2/1 ( “ 1 ; T ) и E ,„ ( “ 2 ; T ), E ^(ю^ T ) и E ^(^ T ), ф E 2/1^ ; T ) и ф E 2/2 ( “ 2 ; T ), E з/1 ( “ 1 ; T ) и £ з,2 ( “ 2 ; T ), E ;,1 ( “ 1 ; T ) и £ ^( “ 2 ; T ), 9 e з/М ; T ) и ф e и(“ 2 ; T )
имеют однотипные зависимости соответственно.
Примем К = m i / ю2. При К = 1 двухчастотная нагрузка преобразуется в одночастотную нагрузку: Ю 1 = m2 = ю, Е 1/1 ( м ; T ) = Ё 1 /2( м ; T ), E *1 ( “ ; T ) = E *2 ( “ ; T ), ф e 1/1 ( “ ; T ) = 9 e 1/2 ( “ ; T ), E 2/1 ( м ; T ) = E 2/2 ( м ; T ) = 1/ 2 E: 2/з ( м ; T ), Е */1 ( м ; T ) = Е */2 ( м ; T ) = 1/ 2 Е */з ( м ; T ), ф е 2/1 ( “ ; T ) =
= ф Е 2/2 ( to ; T ) = ф Е 2/3 ( to ; T ), E 31 ( to ; T ) = E 3/2 ( to ; T ) = 1/ 3 E 3/3 ( to ; T ) = 1/ 3 E 3/4 ( to ; T ), Езп ( го ; T ) =
= Е 3/2 ( to ; T ) = 1/ 3 Е 3/3 ( to ; T ) = 1/ 3 Е 3/4 ( to ; T ), ф е 3/1 ( to ; T ) = ф е 3/2 ( to ; T ) = ф е 3/3 ( to ; T ) = ф е 3/4 ( to ; T ).
При К = 0 двухчастотная нагрузка преобразуется в одночастотную нагрузку с предварительной статической деформацией: ест = а а 1, го1 = 0, го2 = го. В случае если K е [0;1], г г ** т-»* г то E2/3(to1;T) и E2/3(to2;T), E2/3(to1;T) и E2/3(to2;T), фE2/3(to1’T) и фE2/3(to2;T), E3/3 (to1;T)
г ** ** г г и E3/3(to2’T), E3/3(to1’T) и E3/3(to2;T), фe3/3(to1;T) и фe3/3(to2;T), E3/4(to1;T) и E3/4(to2’T),
E 3 * /4( to 1; T ) и E 3 * /4( ro 2; T ), ф E 3/4( to 1 ; T ) и ф E 3/4( ro 2; T ) имеют однотипные зависимости соответственно, которые сдвинуты относительно друг друга в полулогарифмических координатах на величину lg K и на величину 0,5lg K относительно Е 2/1( го 1; T ) и Е 2/2( го 2; T ), * т* г г т-»*
E 2/1( to 1 ; T ) и E 2/2( to 2 ; T )’ ф E 2/1( to 1 ; T ) и ф E 2/2( to 2 ;T ), E 3/1( to 1 ; T ) и E 3/2( ro 2 ’ T ), Е 3/1( го 1 ; T )
* г г m* m*
и E3/2(ro2’ T), фE3/1(ro1; T) и фE3/2(to2’ T), E3/1(to1 ; T) и E3/2 (to2; T), E3/1(to1; T) и E3/2(ro2’ T), фE3/1(to1; T) и фE3/2(го2; T) соответственно.
В качестве функции релаксации можно использовать различные зависимости [8, 20]. Однако определение функции релаксации по результатам гармонических испытаний достаточно сложный и трудоемкий процесс, зависящий от условий эксперимента. С другой стороны, вязкоупругие параметры могут быть определены в условиях сложных воздействий, близких к эксплуатационным, например, путем регистрации зависимостей напряжений и деформаций в образце, испытывающем гармоническое деформирование вида
s ( t ) = е a 1 • sin2 nv 1 1 + е a 2 • sin(2 nv 2 1 + ф g ), (43)
где v - частота ( v = го / 2п); ф g - угол сдвига начальных фаз. Зависимости вязкоупругих параметров от частоты и температуры могут быть описаны полиномами. Полиномиальные модели достаточно просты в практическом применении. Описание объекта с помощью таких моделей легко уточнить, повысив степень полинома.
Для описания поведения вязкоупругого материала при различных значениях температуры может быть использована температурно-временная аналогия (суперпозиция, эквивалентность) [21-24] (в случае стационарных гармонических воздействий ее можно назвать температурно-частотной аналогией), называемая также гипотезой о термореологически простом поведении. Суть данного принципа заключается в том, что вязкоупругие характеристики (функции релаксации и ползучести, комплексные параметры) в полулогарифмических координатах (логарифм времени или частоты) при различных постоянных температурах часто имеют одинаковую форму кривых, но сдвинуты относительно друг друга по логарифмической шкале абсцисс. Если, приняв одну из температур за температуру приведения, сдвигом по логарифмической шкале можно сместить все кривые в одну без существенных погрешностей, тогда возможно использование данного принципа. Величины сдвига описываются функцией температурно-временного смещения. Значения вязкоупругих параметров могут быть определены с помощью преобразований Фурье аналогично работам [25, 26].
В условиях действия двухчастотных нагрузок (43) зависимость (15) может быть записана в следующем виде:
о ( t ) = е a 1 Em ( v 1 ; T ) sin(2 nv ! t + ф E 1/1 ) + £ 2 1 E ^ ( v ; T ) sin(2 nv 1 t ) sin(2 nv ! t + ф e 2/1) + +£ ^ 1 E */1 ( v 1 ; T ) sin(2 nv 1 t ) sin(2 nv 1 t ) sin(2 nv 1 t + ф E 3/1) + +£ a 1 £ a 2 E 2/3 ( v 1 ; v 2 ; T ) sin(2 nv 1 t ) sin(2 nv 2 t + ф g + ф e 2/3 ) + +^ 1 е a 2 E3 /3 ( v 1 ; v 2 ; T )sin(2 nv 1 t )sin(2 nv 1 t + ф e 3/3 )sin(2 nv 2t + ф g ) + +£ a 1 £ 2 2 E */4 ( v 1 ; v 2 ; T ) sin(2 nv 1 t ) sin(2 nv 2 t + ф g + ф e 3/4 ) sin(2 nv 2 t + ф g ) +
+£ a 2 Em ( v 2 ; T ) sin(2 nv 2 t + ф g + ф E 1/2 ) +
+ £ 2 2 E * /2 ( v 2; T ) sin(2 nv 2 t + ф g ) sin(2 nv 2 t + ф E 2/2 + ф g ) + +e ^ 2 E * /2 ( v 2; T )sin(2 nv 2 t + ф g )sin(2 nv 2 t + ф g )sin(2 nv 2 t + ф E 3/2 + ф g ).
После раскрытия скобок получим о (t) = е a 1E^ (v1; T )sin(2nv1t + ф e 1/1) - 0,5ea 1E^ (v1; T )sin(2n2v1t + ф e 2/1 + 0,5n) + +0,5ea 1E*/1 (v1;T) cos(ф e 2/1)- 0,25eaa 1Eз*/1 (v1;T) яп(2п3^+ф e 31)+
+ 0,5 e aa 1 E ^ ( v 1; T ) sin(2 nv 1 t + ф e m ) + 0, 25 е \ 1 E *л ( v 1; T ) sin(2 nv 1 t - ф e m ) -- 0,5 е a 1 £ a 2 E 2*/3 ( v 1; v 2 ; T )sin ( 2 n ( v 1 + v 2 ) t + ф g + ф e 2/3 + 0,5 n ) + + 0,5 e a 1 e a 2 E */3 ( v 1; v 2 ; T ) sin ( 2 n ( v 1 - v 2 ) t - ф g - ф e 2/3 + 0,5 n ) -
- 0, 25 e a 1 е a 2 E 3*/3 ( v 1 ; v 2 ; T ) sin ( 2 n (2 v 1 + v 2 ) t + ф g + ф E 3/3 ) +
+ 0, 25 e a 1 £ a 2 E 3*/3 ( v 1 ; v 2 ; T ) sin ( 2 n (2 v 1 - v 2 ) t - ф g + ф E 3/3 ) +
+ 0, 25 e a 1 £ a 2 E */3 ( v 1 ; v 2 ; T ) sin ( 2 nv 2 t + ф g + ф E 3/3 ) +
+ 0, 25 e a 1 £ a 2 E 3*/3 ( v 1 ; v 2 ; T ) sin ( 2 nv 2 t + ф g - ф E 3/3 ) -
- 0,25 е a 1 £ a 2 E */4 ( v 1; v 2 ; T ) sin ( 2 n (2 v 2 + v 1) t + 2 ф g + ф e 3/4 ) +
+ 0, 25 е a 1 £ a 2 E 3*/4 ( v 1 ; v 2 ; T ) sin ( 2 n (2 v 2 - v 1 ) t + 2 ф g + ф E 3/4 ) +
+ 0, 25 е a 1 £ a 2 E 3*/4 ( v 1 ; v 2 ; T ) sin ( 2 nv 1 t + ф E 3/4 ) + 0, 25 е a 1 £ a 2 E 3^/4 ( v 1 ; v 2 ; T ) sin ( 2 nv 1 t - ф E 3/4 ) + +£ a 2 E */2 ( v 2 ; T ) sin(2 nv 2 1 + ф g + ф E 1/2 ) - 0,5 e a 2 E */2 ( v 2; T ) sin(2 n 2 v 2 1 + 2 ф g + ф e 2/2 + 0,5 n ) +
+ 0,5 e a 2 E */2 ( v 2 ; T ) cos( ф e 2/2 ) - 0,25 8 3 a 2 E* */2 ( v 2 ; T ) sin(2 n 3 v 2 1 + 3 ф g + ф e 3/2 ) +
+ 0,5 e 3 a 2 E* */2 ( v 2 ; T ) sin(2 nv 2 1 + ф g + ф e 3/2 ) + 0,25 e 3 a 2 E *j2 ( v 2 ; T ) sin(2 nv 2 1 + ф g - ф e 3/2 ).
Таким образом, поведение материала при двухчастотных нагрузках описывается двенадцатью гармониками.
В результате, были разработаны полиномиальные зависимости вязкоупругих параметров от температуры и частоты:
E*/1 = b1/0 + b1/1lg v1 + ... + b1/n 1 (lg v1 )n 1,
ЕШ = b1/0 + b1/1lg v2 + ... + b1/n 1 (lg v2 )n 1, фЕ1/1 = b2/0 + b2/1lg v1 + ... + b2/n2 (lg v1 )n2,
'' n 2
ФЕ1/2 — Ь2/0 + b2/1 lg V2 + ... + b2/n2 (lg V2 ) ,
E*/1 = b3/0 + b3/1 lg V1 + ... + b3/n3 (lg V1 )n3 ,(50)
E22 = b3/0 + b3/1 lg V2 + ... + b3/n 3 (lg V2 ) n 3,
Ф Е 2/1 = b4/0 + b4/1 lg V1 + ... + b4/n 4 ( lg V1 ) "\
ФЕ2/2 = b4/0 + b4/1 lg V2 + ... + b4/n4 (lg V2 )”4,
E2*/3 — (1 + b5/1lgK +... + b5/n5 (lgK)n5)(2b3/0 + 2b3/1 lgV2' +... + 2b3/n3 (lgV2)n3),(54)
ФE2/3 = (1 + b6/1 lg K + ... + b6/n6 (lg K)n6 ) (b4/0 + b4/1 lg V2 + ... + b4/n4 (lg V2 )"4 ) ,
E3/1 = b7/0 + b7/1 lg V1 + ... + b7/n7 (lg V1 )n7,
E*/2 = b7/0 + b7/1 lg V2 + ... + b7/n7 (lg V2 )n7,
ФЕ3/1 = b8/0 + b8/1 lg V1 + ... + b8/n8 (lg V1 )n8,
ФЕ3/2 = b8/0 + b8/1 lg V2 + ... + b8/n8 (lg V2 )"8,
E3/3 = (1 + b9/1 lg K + ... + b9/n9 (lg K)n9 )(3b7/0 + 3b7/1 lg V2' + ... + 3b7/n7 (lg V2 )n7 ) ,
ФE3/3 = (1 + b10/1 lg K + ... + b10/n 10 (lg K)n10 ) (b8/0 + b8/1 lg V2' + ... + b8/n8 (lg V2' )n8 ) ,
E*/4 =(1 + bn/1lgK +... + bn/n 11 (lgK)n11 )(3b7/0 + 3b7/1 lgv2'+... + 3b7/n7 (lgV2)n7), (62) ФE3/4 = (1 + b12/1 lg K + ... + b12/n 12 (lg K)n12 ) (b8/0 + b8/1 lg V2 + ... + b8/n8 (lg ^ )n8 ) , lg V1 = lg V1 + lg at ,(64)
lg V2 = lg v2 + lg at ,(65)
lg at — b13/0 + b13/1T + ... + b13/n 13T , lg V2'— lg v2 + lg at + 0,5lg K ,(67)
где n 1, …, n 13 – степени полиномов, b 1/0 , …, b 1/ n 1 , …, b 13/ n 13 – коэффициенты полиномов. Количество коэффициентов, их значения и степени полиномов определяются экспериментально. После выявления полиномиальных зависимостей (46)–(67) необходимо разработать оптимальный план экспериментальных исследований с использованием аппарата теории планирования экспериментов и на основе предложенного плана идентифицировать коэффициенты (46)–(67). После данной процедуры возможно оценить влияние различных вязкоупругих параметров на точность описания поведения материала и в случае их незначительности пренебречь ими.
В более ранних работах [19, 26, 27] была предложена математическая модель описания поведения вязкоупругого материала при двухчастотных нагрузках:
° ( t ) = 8 a 1 E W ( v i ; T ) + 8 a 1 EU ( v i ; T ) sin ( 2 nv i t + ф E 11 ) + 8 21 E 21 ( v i ; T ) sin ( 2 nv i t + ф E 21 ) +
+ 8 a 1 8 a 2 E 2*3 ( v 1 ; v 2 ; T ) sin ( 2 nv 1 t ) sin ( 2 nv 2 t + ф g + ф E 23 ) +
+ 8 a 1 8 a 2 E *3 ( v 1 ; v2; T ) sin ( 2n2v 1 1 + 0,5 n ) sin ( 2nv 2 1 + ф g + ф E 33 ) + + 8 a 1 8 2 2 E *4 ( v 1 ; v 2 ; T ) sin ( 2nv 1 1 ) sin ( 2n2v 2 1 + 2ф g + ф E 34 + 0,5 n ) + + 8 a 2 E V 2 ( v 2 ; T ) sin ( 2 nv 2 t + ф E 12 ) + 8 22 E *2 ( v 2 ; T ) sin ( 2 nv 2 t + Ф E 22 ) ,
для которой было принято допущение, что динамические нагрузки, действующие на фоне квазистатических, не приводят к большим деформациям, поэтому существенных искажений петли гистерезиса от эллиптической формы не происходит. Исходя из этого при одно-и двухчастотном нагружениях дополнительных частот (2 ν 1 , 3 ν 1 , 2 ν 2 , 3 ν 2 ), помимо основных ν 1 и ν 2 , не возникает. При этом остается существенной зависимость вязкоупругих параметров от амплитуд деформации ε а 1 и ε а 2 . В работах [19, 28] данные зависимости были описаны линейными функциями. Отсутствие дополнительных частот не позволяет учесть различное сопротивление при растяжении и сжатии. Для учета разносопротивляемости материала был введен дополнительный параметр E * 10 , который смещает напряжения в сторону большего сопротивления (в область сжатия) [26]. Кроме того, при стационарных гармонических нагрузках для данного типа материалов наблюдаются зависимости вязкоупругих параметров от предварительной статической деформации [19, 29]. В связи с этим в случае двухчастотных воздействий появляются дополнительные гармоники (параметры E * 23 , E * 33 , E * 34 ). Значениями параметра E * 34 в (68) пренебрегаем. При ε а 1 > ε а 2 E * 34 пренебрежимо мал, а при ε а 1 < ε а 2 отсутствие параметра E * 34 компенсировалось изменениями E * 10 .
Допущения о линейной зависимости вязкоупругих параметров от амплитуд деформации и об отсутствии искажений петли гистерезиса, а также пренебрежение параметром E * 34 могут быть не характерны для других материалов. Так, например, если в результате исследования будут наблюдаться существенные искажения формы петли гистерезиса, модель (68) не сможет это учесть. В этом смысле математическая модель (44), представленная в данной статье, более предпочтительна к использованию.
Резюмируя, скажем, что для исследуемого типа вязкоупругих материалов в той или иной степени наблюдается нелинейное поведение, а также различное сопротивление растяжению и сжатию (разносопротивляемость) [30]. Поведение таких материалов при двухчастотных нагрузках может быть описано восемнадцатью вязкоупругими параметрами E 1/1 , E 2/1 , E 3/1 , E 2/3 , E 3/3 , E 3/4 , E 1/2 , E 2/2 , E 3/2 , φ E 1/1 , φ E 2/1 , φ E 3/1 , φ E 2/3 , φ E 3/3 , φ E 3/4 , φ E 1/2 , φ E 2/2 , φ E 3/2 . В случае если нелинейные эффекты и разносопротивляемость не существенны, значения параметров E * 2/1 , E * 3/1 , E * 2/3 , E * 3/3 , E * 3/4 , E * 2/2 , E * 3/2 , φ E 2/1 , φ E 3/1 , φ E 2/3 , φ E 3/3 , φ E 3/4 , φ E 2/2 , φ E 3/2 будут стремиться к нулю.
2. Экспериментальные исследования
Экспериментальные исследования были проведены в ЦКП «Центр экспериментальной механики ПНИПУ» на электродинамической испытательной системе Instron ElectroPuls E10000 с использованием температурной камеры Instron 3119. В испытаниях использовался высоконаполненный эластомер марки «ПДИ» (имитатор твердого топлива, НИИ полимерных материалов, г. Пермь) [27].
Вязкоупругие параметры материала определялись для установившегося режима деформирования (после выхода на заданный режим испытательной системы). Для реализации изотермического нагружения образца температурная камера работала в течение всего времени проведения экспериментов. Для уменьшения влияния разогрева образца на определяемые параметры время проведения эксперимента было ограничено по количеству циклов (в зависимости от вида воздействия) [27].
При определении вязкоупругих параметров материала учитывалась жесткость элементов экспериментальной установки вследствие того, что перемещения, фиксируемые используемым датчиком, складываются из перемещений образца и перемещений элементов этой системы [27].
Для подобных материалов характерна разносопротивляемость, поэтому перемещения элементов системы при сжатии образца больше , чем при его растяжении. С понижением температуры опыта и увеличением частоты нагружения перемещения элементов экспериментальной системы и, следовательно, искажение задаваемого сигнала становятся существеннее . Поэтому, при необходимости вносились корректировки в закон деформирования образца.
Нужно также отметить, что геометрия образцов существенно влияет на определяемые вязкоупругие параметры, так как при нагружении в образце возникает сложное неоднородное напряженно-деформированное состояние . Для учета влияния геометрического фактора на определяемые параметры были решены динамические осесимметричные задачи в программном обеспечении ANSYS, которые соответствуют экспериментальной ситуации. В результате были определены поправочные коэффициенты [27]. Вязкоупругие параметры материала определялись с использованием преобразования Фурье аналогично работам [25–27].
Как уже отмечалось, для описания зависимости вязкоупругих параметров от частоты нагружения и температуры опыта были использованы полиномы (46)–(67). Для определения этих полиномиальных зависимостей были проведены экспериментальные исследования (таблица), результаты которых представлены на рис. 1–11.
План экспериментальных исследований The experimental design
|
Амплитуды деформации |
Частоты |
Температура |
||||||
|
ε а 1 , % |
ε а 1 , % |
ν 1 |
ν 2 |
Т 1 |
Т 2 |
Т 3 |
Т 4 |
Т 5 |
|
3 |
3 |
0,1 |
1 |
50 |
30 |
3 |
–20 |
–50 |
|
0,01 |
0,1 |
|||||||
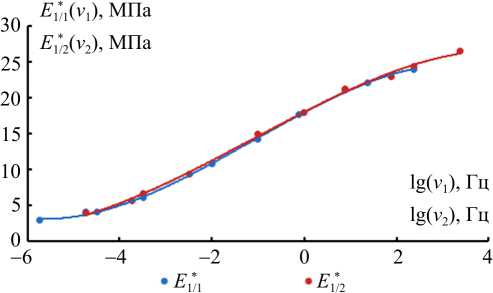
Рис. 1. Зависимости параметров E* 1/1 , E* 1/2 от частоты при температуре 3 °С Fig. 1. The dependences of parameters E* 1/1 , E* 1/2 on frequency at the temperature of ( T = 3 °С)
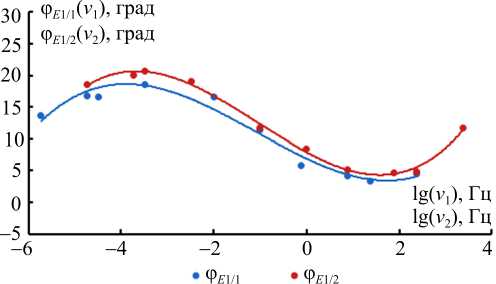
Рис. 2. Зависимости параметров φ E 1/1 , φ E 1/2 от частоты при температуре 3 °С Fig. 2. The dependences of parameters φ E 1/1 , φ E 1/2 on frequency at the temperature of ( T = 3 °С)
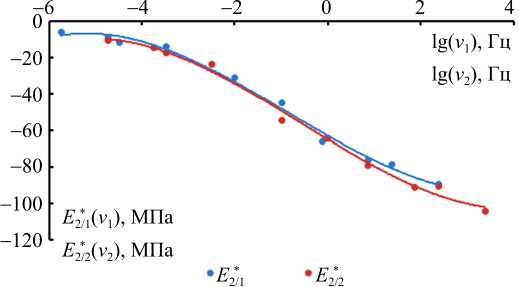
Рис. 3. Зависимости параметров E* 2/1 , E* 2/2 от частоты при температуре 3 °С Fig. 3. The dependences of parameters E* 2/1 , E* 2/2 on frequency at the temperature of ( T = 3 °С)
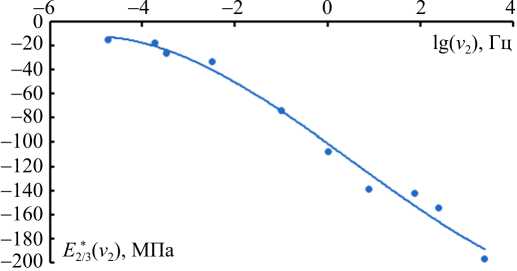
Рис. 4. Зависимости параметра E* 2/3 от частоты ν 2 при температуре 3 °С Fig. 4. The dependences of parameter E* 2/3 on frequency at the temperature of ( T = 3 °С)
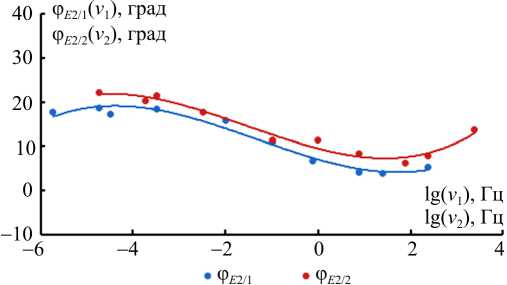
Рис. 5. Зависимости параметров φ E 2/1 , φ E 2/2 от частоты при температуре 3 °С Fig. 5. The dependences of parameters φ E 2/1 , φ E 2/2 on frequency at the temperature of ( T = 3 °С)
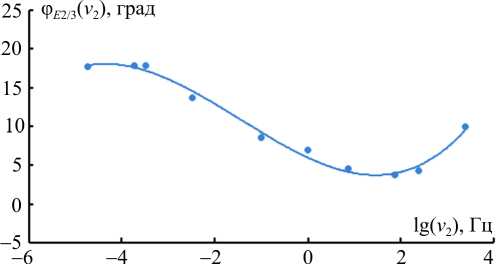
Рис. 6. Зависимости параметра φ E 2/3 от частоты ν 2 при температуре 3 °С Fig. 6. The dependences of parameter φ E 2/3 on frequency at the temperature of ( T = 3 °С)
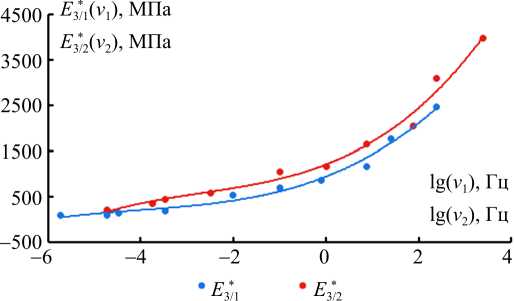
Рис. 7. Зависимости параметров E* 3/1 , E* 3/2 от частоты при температуре 3 °С Fig. 7. The dependences of parameters E* 3/1 , E* 3/2 on frequency at the temperature of ( T = 3 °С)
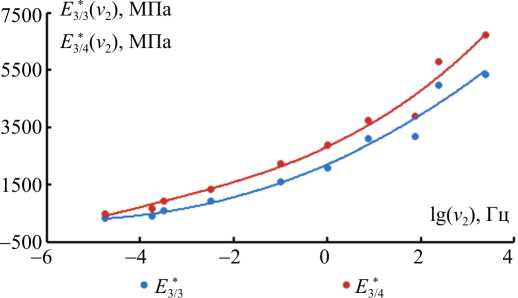
Рис. 8. Зависимости параметров E* 3/3 , E* 3/4 от частоты ν 2 при температуре 3 оС Fig. 8. The dependences of parameters E* 3/3 , E* 3/4 on frequency at the temperature of ( T = 3 оС)
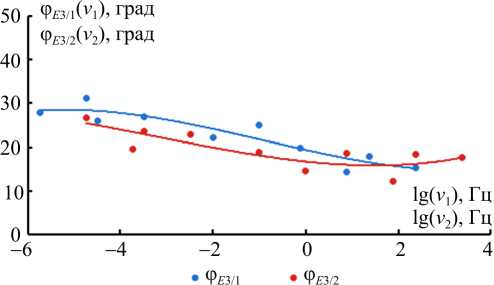
Рис. 9. Зависимости параметров φ E 3/1 , φ E 3/2 от частоты при температуре 3 оС Fig. 9. The dependences of parameters φ E 3/1 , φ E 3/2 on frequency at the temperature of ( T = 3 оС)
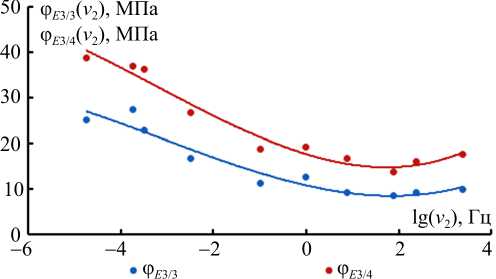
Рис. 10. Зависимости параметров φ E 3/3 , φ E 3/4 от частоты ν 2 при температуре 3 оС Fig. 10. The dependences of parameters φ E 3/3 , φ E 3/4 on frequency at the temperature of ( T = 3 оС)
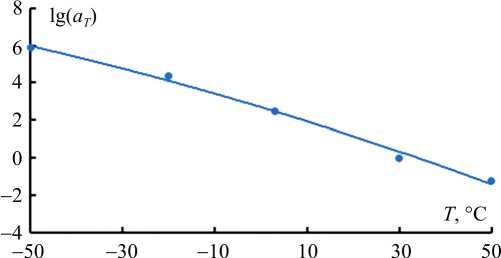
Рис. 11. Зависимость lg a T от температуры
Fig. 11. The dependence of lg a T on the temperature
Заключение
Рассмотрена математическая модель, описывающая линейное поведение вязкоупругих материалов в форме интегральных операторов, а также математическая модель, описывающая нелинейное поведение вязкоупругих материалов в виде интегрального ряда Вольтерра–Фреше. На основе нелинейного представления Вольтерра–Фреше предложена модель для описания нелинейного поведения материала в условиях действия стационарных одночастотных и двухчастотных нагрузок с использованием комплексных параметров. Проведен анализ математической модели для описания зависимостей вязкоупругих параметров от частот нагружения и температуры, предложены полиномиальные зависимости с использованием температурно-временной аналогии (суперпозиции, эквивалентности). Проведены экспериментальные исследования, после обработки которых были выявлены зависимости вязкоупругих параметров от частот нагружения и температуры. Полученные результаты позволяют разработать оптимальный план экспериментальных исследований (с использованием аппарата теории планирования экспериментов), с помощью которого с достаточной точностью будут определены коэффициенты предложенной модели. Далее возможна оценка влияния различных вязкоупругих параметров на точность описания поведения материала в условиях действия гармонических нагрузок.
Работа выполнена при финансовой поддержке РФФИ (грант 16-31-00230 мол_а).
Список литературы Математическая модель и экспериментальные исследования поведения вязкоупругих наполненных полимеров при двухчастотных воздействиях
- Косточко А.В., Казбан Б.М. Пороха, ракетные твердые топлива и их свойства: учеб. пособие. -М.: Инфра-М, 2014. -400 с.
- Ерохин Б.Т. Теория и проектирование ракетных двигателей: учебник. -СПб: Лань, 2015. -608 с.
- Yavor Y., Gany A., Beckstead M. Modeling of the agglomeration phenomena in combustion of aluminized composite solid propellant//Propellants, Explosives, Pyrotechnics. -2014. -Vol. 39. -Iss. 1. -P. 108-116.
- Фахрутдинов И.Х., Котельников А.В. Конструкция и проектирование ракетных двигателей твердого топлива: учебник для машиностроительных вузов. -М.: Машиностроение, 1987. -328 с.
- Внутренняя баллистика РДТТ/А.В. Алиев . -М: Машиностроение, 2007. -504 с.
- Методы прикладной вязкоупругости/А.А. Адамов, В.П. Матвеенко, Н.А. Труфанов, И.Н. Шардаков. -Екатеринбург: Изд-во УрО РАН, 2003. -411 с.
- Кристенсен Р. Введение в теорию вязкоупругости. -М.: Мир, 1974. -338 с.
- Работнов Ю.Н. Элементы наследственной механики твердых тел. -М.: Наука, 1977. -384 с.
- Euler L. Introductio in analysin infinitorum. -Lausanne, 1748. -320 p.
- Unique nonlinear behavior of nano-filled elastomers: From the onset of strain softening to large amplitude shear deformations/A. Papon, S. Merabia, L. Guy, F. Lequeux, H. Montes, P. Sotta, D.R. Long//Macromolecules. -2012. -Vol. 45. -Iss. 6. -P. 2891-2904.
- Dorfmann A., Pancheri F.Q. A constitutive model for the Mullins effect with changes in material symmetry//International Journal of Non-Linear Mechanics. -2012. -Vol. 47. -Iss. 8. -P. 874-887.
- Морозов И.А., Свистков А.Л. Структурно-феноменологическая модель механического поведения резины//Механика композиционных материалов и конструкций. -2008. -Т. 14, № 4. -С. 583-596.
- Semkiv M, Long D, Hütter M. Concurrent two-scale model for the viscoelastic behavior of elastomers filled with hard nanoparticles//Continuum Mechanics and Thermodynamics. -2016. -Vol. 28. -Iss. 6. -P. 1711-1739. DOI 10.1007/s00161-016-0504-3
- Loaded rubber-like materials subjected to small-amplitude vibrations/T. Beda, J.B. Casimir, K.E. Atcholi, Y. Chevalier//Chinese Journal of Polymer Science (English Edition). -2014. -Vol. 32. -Iss. 5. -P. 620-632.
- Influence of orthogonal prestrain on the viscoelastic behavior of highly filled elastomers/A. Azoug, A. Thorin, R. Neviere, R.M. Pradeilles-Duval, A. Constantinescu//Polymer Testing. -2013. -Vol. 32. -Iss. 2. -P. 375-384.
- Jalocha D., Constantinescu A., Neviere R. Prestrained biaxial dma investigation of viscoelastic nonlinearities in highly filled elastomers//Polymer Testing. -2015. -Vol. 42. -P. 37-44.
- Lakes R. Viscoelastic Materials. -Cambridge University Press, 2009. -461 p.
- Brinson H.F., Brinson L.C. Polymer Engineering Science and Viscoelasticity. -Springer Science + Business Media, 2008. -446 p.
- Особенности поведения низкомодульных вязкоупругих полимерных композитов при варьировании амплитуды деформации низкочастотной составляющей бигармонической нагрузки/А.С. Янкин, Р.В. Бульбович, С.В. Словиков, В.Э. Вильдеман//Вестник Пермского национального исследовательского политехнического университета. Механика. -2014. -№ 3. -С. 231-248.
- Колтунов М.А. Ползучесть и релаксация. -М.: Высш. шк., 1976. -277 с.
- Williams M.L., Landel R.F., Ferry J.D. The temperature dependence of relaxation mechanisms in amorphous polymers and other glass-forming liquids//Journal of the American Chemical Society. -1955. -Vol. 77. -Iss. 14. -P. 3701-3707.
- Menard K.P. Dynamic Mechanical Analysis: A Practical Introduction. Second Edition. -CRC Press, 2008. -240 p.
- Challenges in Mechanics of Time Dependent Materials, Vol. 2: Proceedings of the 2016 Annual Conference on Experimental and Applied Mechanics/B. Antoun, A. Arzoumanidis, H.J. Qi, M. Silberstein, A. Amirkhizi, J. Furmanski, H. Lu. -Springer, Technology & Engineering. -2016. -217 p.
- Cho K.S. Viscoelasticity of Polymers: Theory and Numerical Algorithms. -Springer, Technology & Engineering. -2016. -612 p.
- Янкин А.С., Словиков С.В., Бульбович Р.В. Определение динамических механических свойств низкомодульных вязкоупругих композитов при бигармоническом законе нагружения//Механика композиционных материалов и конструкций. -2013. -Т. 19, № 1. -С. 141-151.
- Вязкоупругие характеристики высоконаполненных полимерных композитов при двухчастотных воздействиях/А.С. Янкин, Р.В. Бульбович, С.В. Словиков, В.Э. Вильдеман, В.В. Павлоградский//Механика композитных материалов. -2016. -Т. 52. -№ 1. -С. 115-128.
- Янкин А.С. Влияние частот бигармонического (двухчастотного) нагружения на механическое поведение имитатора твердого топлива//Вестник Пермского национального исследовательского политехнического университета. Механика. -2015. -№ 4. -С. 273-292 DOI: 10.15593/perm.mech/2015.4.16
- Влияние амплитуды деформации высокочастотной составляющей бигармонического (двухчастотного) закона нагружения на динамические механические свойства низкомодульных вязкоупругих композитов/А.С. Янкин, Р.В. Бульбович, С.В. Словиков, В.Э. Вильдеман//Механика композитных материалов. -2013. -Т. 49, № 6. -С. 1005-1012.
- Белкина М.А., Бульбович Р.В. К постановке задачи об исследовании деформационных свойств ТРТ при нестационарном нагружении. Аэрокосмическая техника и высокие технологии -2000//Тез. докл. Всерос. науч.-техн. конф./под ред. Ю.В. Соколкина и А.А. Чекалкина. -Пермь: Изд-во Перм. гос. техн. ун-та, 2000. -С. 24.
- Москвитин В.В. Сопротивление вязкоупругих материалов применительно к зарядам ракетных двигателей на твердом топливе. -М.: Наука, 1972. -328 с.


