Математическая модель импульсного сканирования давления по длине пьезоэлектролюминесцентного оптоволоконного датчика

ВЕСТНИК ПНИПУ. МЕХАНИКА № 1, 2018PNRPU MECHANICS BULLETIN

Сенсорика за последние годы сформировалась в самостоятельную высокотехнологичную ветвь измерительной техники [1], одной из центральных задач которой является разработка все более совершенных датчиков для диагностирования различных физико-механических параметров исследуемых объектов. К новым датчикам предъявляются все более высокие требования. В частности, наряду с высокими метрологическими характеристиками особое значение придается их высокой надежности, долговечности, стабильности, малым габаритам, массе и энергопотреблению, возможности встраивания в объекты и системы мониторинга, совместимости с микроэлектронными и компьютерными устройствами обработки информации, низкой себестоимости, что в наибольшей степени характеризует именно оптико-электронные волоконные датчики. В [1] рассмотрены классификация, принципы действия, конструкции, параметры и характеристики оптикоэлектронных и волоконно-оптических датчиков, дан анализ влияния различных факторов на характеристики датчиков и приведены принципиальные схемы построения электронных и оптических датчиков для решения различных промышленных, технологических и медицинских задач. Различие между активными и пассивными датчиками обусловлено различием принципов их функционирования, отражающих, в свою очередь, фундаментальные отличия: активные датчики сами являются генераторами информативного выходного сигнала различной физиче- ской природы, пассивные - имеют лишь информативное воздействие на процесс, в частности, через изменение удельного сопротивления изменяется сила электрического тока в проводнике или через изменение показателя преломления оптоволокна (световода) изменяются выходные характеристики светового потока. В активном пьезоэлектрическом датчике параметр измерения, в частности внешнее давление, воздействует на пьезоэлектрический элемент, что приводит к деформации и появлению на его гранях электрических зарядов противоположного знака, величина которых связана с измеряемым давлением. Световод может использоваться в качестве линии передачи информативного сигнала и/или чувствительного элемента, в частности, в виде участка световода с дифракционной решеткой Брэгга [2-6]; механолюминесцентный эффект использован в конструкциях датчиков [7]. В [8-11] представлены результаты теоретических и экспериментальных исследований по оценке механических свойств и деформаций полимерных композиционных материалов с помощью интегрированных в структуры материалов оптических волокон с решетками Брэгга. В [12] найдено распределение деформации по длине оптоволоконного датчика, и установлена минимально допустимая длина датчика для различных случаев нагружений в результате численного моделирования деформационных процессов в системе «подложка-клей-оптоволоконный датчик» в рамках линейной теории термовязкоупругости. Возможность измерения градиентных полей деформаций волоконнооптическими датчиками с решетками Брэгга продемонст- рирована в [13] на примере пластины с вырезами в сравнении с результатами, полученными при использовании трехмерной цифровой оптической системы, и с результатами численного моделирования методом конечных элементов. Оценки технологических деформаций в полимерных композиционных образцах с использованием внедренных волоконно-оптических датчиков с решетками Брэгга даны в [14]. Другим перспективным решением проблемы диагностирования неоднородных полей деформаций и наличия дефектов в элементах композитных конструкций являются сенсорные пьезоэлектрические сети [15–17], внедренные в структуру конструкции. Моделирование процессов в пьезоэлектрических чувствительных элементах датчиков проводится на основе решений соответствующих связанных краевых задач электроупругости аналитическими [18–21] или численными [22–26] методами механики сплошной среды. В [27–30] предложены новые конструкции пьезоэлектролюминесцентных оптоволоконных датчиков для уточненного диагностирования давления [27–29] и сложного объемного напряженно-деформированного состояния композитных конструкций [30] с использованием алгоритмов [28, 29] обработки приемником-анализатором интегральных оптических сигналов на выходе из световода датчика. Информативный световой сигнал возникает на локальном участке датчика в силу механолюминесцентного эффекта, обусловленного взаимодействием пьезоэлектрического и электролюминесцентного слоев датчика, и передается по световоду к приемнику-анализатору; наличие управляющих электродов позволяет диагностировать локации неоднородностей давления по длине датчика.

Цель – разработка математической модели импульсной локации неоднородностей давления по длине оптоволоконного пьезоэлектролюминесцентного датчика [27] с использованием локационного сканирующего электрического видеоимпульса на управляющих электродах по результатам замеряемой на торцевом сечении волоконного датчика интенсивности исходящего из оптоволокна света для различных моментов времени; для частного случая – сканирования предельно узким импульсом – получить аналитическое решение для диагностируемого неоднородного давления, что значительно упростит известный алгоритм [29] обработки светового сигнала на выходе из оптоволокна датчика.

1.    Оптоволоконныйпьезоэлектролюминесцентный датчик

Датчик давления (рис. 1) [27–29] представляет собой составное слоистое волокно, состоящее из оптоволокна 1, электролюминесцентного 2 и с радиальной поляризацией пьезоэлектрического 3 цилиндрических концентрических слоев с внутренним фотопрозрачным, в частности, перфорированным или сеточным 4 и внешним 5 непрерывными управляющими электродами. Действие радиального напряжения (давления) а, на некотором локальном участке внешней боковой поверхности датчика приводит к соот- ветствующим деформациям участка пьезоэлектрического слоя 3 и появлению в нем и в смежном с ним локальном участке электролюминесцентного слоя 2 электрического поля, приводящего к свечению локального участка электролюминесцентного слоя внутрь (через фотопрозрачный электрод 4) оптоволокна 1; управляющие электроды 4, 5 с напряжением U упр дают возможность изменять, в част ности, однородно или неоднородно по длине датчика электрическое напряжение на электролюминесцентном слое 2 и как результат величину интенсивности света I на выходе из оптоволокна.

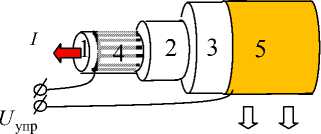
Рис. 1. Датчик давления а , с управляющим напряжением U _упр и интенсивностью света I на выходе из световода Fig. 1. Sensor of pressure a , with the operating voltage U упр and intensity of light I at the exit from the light guide

2.    Математическая модель сканирования

Рассмотрим процесс сканирования неоднородного давления a ( z ) по оси датчика z e (0; 1 ) локационным электрическим управляющим напряжением U _упр ( z , t ) на электродах, которое представим в виде суммы некоторого постоянного по длине значения U ₀ и локационного электрического видеоимпульса прямоугольной формы U ₁ ( z , t ), распространяющегося в положительном направлении оси z .

U упр ( z , t ) = U 0 + U 1 ( z , t )                 (1)

В произвольный момент времени t 1 e (0; T ) импульсная функция U ₁ ( z , t ₁ ) отлична от нуля и равна значению U ₁ лишь на локальном участке l ₁ с координатами z с ( z 1 - 1 1 / 2; z 1 + 1 1 /2) и длиной 1 1 с центром в точке z 1 = z ₀ + ct 1 , где координаты начального и конечного положений центра импульса z ₀ ^ 1 1 /2 и 1 - 1 1 /2 соответственно, координата z e (0; 1 ); длина электрода l ; время прохождения центром одиночного импульса от начального до конечного положений T = ( 1 - 1 1 )/ c ; скорость распространения импульса c .

Таким образом, для диагностики давления а,1 на участке l1 с центром z1 имеем (после проведенных в n циклах диагностики замеров интенсивностей света на выходе оптоволокна) функцию I = I(Uупр1), заданную через узловые значения интенсивности света I(k) ^ I (tk) на выходе оптоволокна и управляющего напряжения на участке 11 Uупр1(k) = U0 + U1(k), где моменты времени прохождения импульсом этого участка tk = (z1 - z 0) / c + (k - 1)T. Однородная составляющая U0 и величина импульса Uцk) =-U1 a + A U1(k -1) постоянны в течение каждого цикла k = 1, n диагностики и варьируются, в частности увеличиваются на некоторую малую величину AU1 лишь при начале следующего цикла для случая U1 е [-U1 a; U1 a ], где минимальное и максимальное значения U1(1,n) = + U1 a; амплитуда импульса U 1 a > 0; n - число циклов диагностики.

Рассмотрим вероятностную модель, в которой распределение действующего на боковую цилиндрическую поверхность волоконного датчика внешнего давления а ( z ) по координате z описываем непрерывной случайной величиной а , , реализациями которой являются различные значения действующего давления а ( z ), где z е (0; 1 ); аналогично для случайной величины о 1 , реализациями являются различные значения а ( z ) на соответствующем локальном участке z е 1 1 датчика. Электрическое напряжение на электролюминесцентном локальном участке l ₁ датчика

U 1 , = an упр1 + a 2 ^ 1 .                 (2)

также является случайной величиной, связанной с давлением о1, параметрами датчика a1, a2. Найдем функции плотности f, (Z1) распределения этого давления а1, по анализу интенсивности света I на выходе из оптоволокна датчика. Считаем, что свойства электролюминесцентного элемента заданы «S-образной» кривой зависимости интенсивности свечения I = I (U) от приложенного напряжения U с характерными точками заданных пороговых напряжений: Umin для начала свечения и Umax для начала насыщенного свечения электролюминесцентного элемента (рис. 2).

Алгоритм расчета функции плотности распределения f 1 , ( Z 1 ) давления на локальном участке оптоволоконного датчика рассмотрен в [29], согласно которому искомая функция f , ( Z 1 ) является решением интегрального уравнения Фредгольма 1-го рода

-A-= a l У/х й ) ^{d U} упр1 ¹ ^min \

V f . ( Z 1 ) d Z 1 , I U = ^a 1 U упр1 ^{+ a} 2 ^ 1

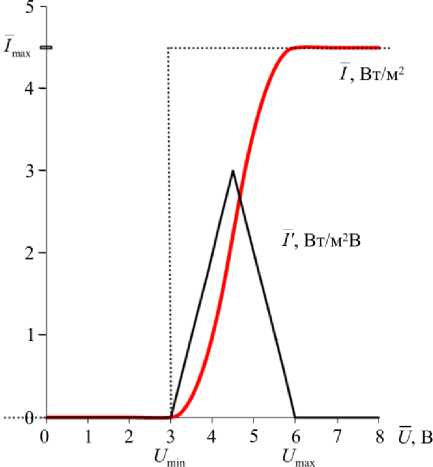
Рис. 2. Заданная функция I и производная I ' интенсивности свечения электролюминесцентного элемента от значений приложенного напряжения U

Fig. 2. The set function I and derivative I ' of luminescence intensity of the electroluminescent element on the values of the enclosed voltage U

где границы интегрирования

Z 1min =Z 1 (0) = ( U (0) - ^U упр1 ) / a 2 ,

1max

^Z 1 ⁽ I max ) ^{( U (} I max ) ^a 1 ^U упр1 ) / ^a 2

• с учетом (2). В каноническом виде интегральное уравнение Фредгольма (3) имеет вид

smax f (x) = j K (x - 5)y(5)ds ,(5)

smin где разностное ядро nJ, —

K(x - s) = -111'(x - s)(6)

a2l с учетом новых переменных x = a1Uупр1 , s = -a2z1, известная f (x) ^

'  dI vd U упр1

с учетом (7) и иско-

I ^U упр1 = ^x / ^a 1

мая y ( s ) ^ f 1 , ( Z 1 )i функции, границы интегрирова- 1 5 1 =- s / a '2

ния: smin = x - U(Imax ) , smax = x - U(0) или smin ^ Z , smax = x с учетом (4), U(0) = 0 , U(Imax) ^ ” . Различные аналитические и численные методы решения интегральных уравнений Фредгольма (5) даны в [31–35]. В частном случае, когда зависимость I = I (U) - ступенчатая функция (пунктирная линия на рис. 2), произ- водная в ядре (6) уравнения (5) выражается

I '(U ) = I max 8(U - U min ) через дельта-функцию Дирака и из (3) получим решение для искомой функции плотности распределения

I U упр1 = ⁽ U min ^- a 2 ^ 1)/ ^a 1

где константа к 1 - a ₂ /( a₁1 _1max); максимальная интенсивность свечения 1 _1max ^ I _max 1 1 / 1 участка электролюминесцентного элемента оптоволоконного датчика длиной l ₁ .

Для случая, когда на рассматриваемом участке z' e 11 диагностируемое давление a1e = const или когда ширина l1 сканирующего импульса является предельно малой величиной (11 = Az -^ l) и давление CT1, (z') ® const для z' e (z; z + Az), функция плотности распределения вырождается к виду f,(Z1 )=5(Z1 -Q1.)                (9)

и из интегрального (3), (5) получим алгебраическое уравнение aa=arI '(U)-       ,        (10)

^d U упр1       ¹            U = ^aU упр1 ⁺ a 2 ° 1 *

функция интенсивности свечения I на выходе из оптоволокна

l

I U упр1 ) = 1 0 + 7 1 U )|          ,       (11)

1         U=aU упр1+ a 2^1, где Iо = 10(Uо) обусловлено возможным свечением участка 10 = 1 \ 11. В частности, значение U0 в (1) может быть подобрано из условия I0 = 0 отсутствия свечения на выходе из световода в отсутствие импульса. В результате получим искомое решение для величины диагностируемого давления ab=( I-1(Л) - axU) / a 2,           (12)

где I ^-1 - функция, обратная известной I = I (U ) (см. рис. 2) величина

Л ¹ ( I (U упр1 ) - I о )                 (13)

l ₁

выражается через экспериментально измеренную интенсивность I(Uупр1) для соответствующего значения управляющего напряжения Uупр1 . Отметим, что в (12) CT1, = ст. (z) - это давление в малой окрестности внешней границы сечения датчика с координатой z ; величина Л рассчитывается через интенсивность света I на выходе из световода в момент времени t = 2z / c, где c – скорость распространения электрического импульса (света), начальный момент времени t = 0 соответствует моменту входа импульса в датчик.

• 3.    Области допустимых значений параметров управляющего напряжения

Для диагностики оптоволоконным датчиком значений давления ст , из всего рабочего диапазона ( CT _min; CT _max) необходимо выполнение условий: во-первых, минимальное значение управляющего сигнала U _упр(min) должно приводить к прекращению свечения ( U , ^ U _min) даже на участке, где действует максимальное давление CT max , и, во-вторых, максимальное значение управляющего сигнала U _упр(max) должно приводить к максимальному «насыщенному» свечению ( U , >  U _max ) даже на участке, где действует минимальное давление CT _min. Эти условия с учетом того, что напряжение на электролюминесцентном элементе, например на участке l ₁ действия импульса, имеет вид U , 1 ( t ) = a 1 U _упр1 ( t ) + a ₂ ст , 1 (2), запишем как систему неравенств

I ^a1^U упр1(min) ⁺ a 2 ^CT 1(max) ^ ^U min ,            (14)

[ a1Uупр1(max) + a2CT1(min) ^ Umax с использованием заданных пороговых напряжений Umin для начала свечения и Umax для начала насыщенного свечения электролюминесцентного элемента. Для случая, когда величина импульса U1 e (-U1 a; U1 a), систему (14) преобразуем к виду

I ^a 1 ^{( U} 0(min) ^{- U} 1 a ) ⁺ a 2 ^CT 1(max) ^ ^U min ,        (15)

I a1 (U0(max) + U1 a ) + a2CT1(min) ^ Umax с учетом равенств Uупр1(min) = U0(min) - U1 a, UуПр1(max) = = U0(max) + U1 a (1), амплитуды импульса U1 a > 0 и допуская для общего случая вариации однородной составляющей управляющего напряжения U0 на интервале значений (U0(min);U0(max)). Таким образом, область допустимых значений параметров управляющего сигнала найдем из решения системы

^U 0(min) ^{- U} 1 a ^ b 1 ,

' ^U 0(max) ^{+ U} 1 a ^ b 2 ,                  ⁽¹⁶⁾

U1 a ^ 0, где коэффициенты b1 = (Umin - a2CT1(max) ) / a1, b2 = ( Umax - a2 CT1(min) ) / a1              (17)

с учетом того, что a₁₂ >  0 .

Для случая, когда U 0 = const, в (15), (16) полагаем равенства и ₀₍ mi _n) = и 0(max) = и 0 :

U 0 - U 1 a ^ b l ,

^ U 0 + U 1 a У b 2 ,

U 1 a У 0.

В частности, при U ₀ = 0 амплитуда импульса выбирается из области допустимых значений (16)

^{U 1} a ^{У -} b ^{1 ,}

1 U 1 a У b 2 ,                       (19)

. U 1 a У 0.

Для случая, когда U 1 a = 0 импульс отсутствует, область допустимых значений границ U _0(min) , U _0(max) для варьирования величины однородной составляющей управляющего напряжения U ₀ находим из системы

^U 0(min) ^ ^b1 ,

^U 0(max) ^У b 2 .

4.    Результаты численного моделирования

Численный расчет области допустимых значений параметров: U ₀ , U _{1 a} управляющего напряжения на рис. 3 проведен (18) для значений границ: Hu mi n) = 70кПа, ст ₁ ( _max ) = 80 кПа действующего на участке 1 1 давления а _{1 е} , пороговых напряжений для начала U _min = 3 В и насыщенного U _max = 6 В свечений электролюминесцентного элемента (см. рис. 2), параметров датчика a 1 = 0,972, a ₂ = 0,235 - 10 — 4 В/Па [28, 29] и рассчитанных значений коэффициентов Ь 1 « 1,152 В, b ₂ ® 4,480 В (17). Вертикальным красным отрезком на рис. 3 обозначены допустимые значения U 1 _a У b ₂ амплитуды импульса для случая (19) отсутствия ( U ₀ = 0) однородной составляющей в управляющем напряжении (1).

На рис. 4, а построены зависимости интенсивности света I = I(Uупр1) (с учетом I0 (0) = 0 , где интенсивность свечения I0 = I0(U0) участка 10 = 1 /11, который светится лишь при значении U0 > U1 = 0,91 В) и производной I' = dI / dUупр1 на выходе из оптоволокна от управляющего напряжения Uупр1 при заданном равномерном законе распределения f1, (Z1) действующего давления о1е е (ст '1; ст '2) на участке 11 в границах ст '1 = 70кПа, ст '2 = 80 кПа с параметрами датчика a1 = 0,972, a2 = 0,235 -10-4 В/Па, относительной длиной 11 /l = 0,01 участка 11. Значение амплитуды им пульса U1 a = 5 В (U0 = 0) было выбрано с учетом области допустимых значений параметров управляющего напряжения (см. рис. 3). Пунктирные графики (см. рис. 4, а) зависимостей интенсивности света I и производной I ' от управляющего напряжения Uупр1 на участке 11 построены для случая, когда функция I = I (U) задана в виде ступенчатой функции (см. рис. 2) с параметрами Imax = 4,5 Вт/м2, Umin = 3В.

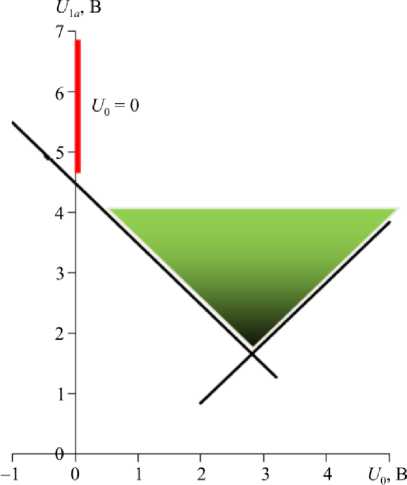
Рис. 3. Область допустимых значений параметров

U ₀ , U _{1 a} управляющего напряжения

Fig. 3. Domain of admissible values of parameters:

U ₀ , U _{1 a} of operating voltage

На рис. 4, б для случая наличия лишь однородной по длине датчика составляющей варьируемого управляющего напряжения U ₀ в отсутствие импульса ( U 1 a = 0) построены зависимости интенсивности света I и производной I ' = dI / dU ₀ (5) на выходе из оптоволокна от управляющего напряжения U ₀ при заданном равномерном законе распределения f , ( Z ) действующего давления ст , е ( ст 1 ; ст ₂) по всей длине 1 в границах ст 1 = 30 кПа, ст ₂ = 90кПа. Допустимые значения границ U _0(min) , U _0(max) варьирования величины управляющего напряжения U ₀ е ( U ₀ ( _min ) ; U ₀ ( _max ) ) найдены из решения (20). Пунктирные графики на рис. 4, б рассчитаны для случая, когда функция I = I (U ) задана в виде ступенчатой функции (см. рис. 2). Граничные значения давлений ст 1 ₂ связаны с соответствующими характерными значениями U _1,2 управляющего напряжения U ₀ зависимостью ст 1 ₂ ^ ( U _min - a 1 U ₂ 1 ) / a ₂ с учетом (2); для рассматриваемого случая (см. рис. 4, б) имеем значения U 1 = 0,91 В, U ₂ = 2,36 В.

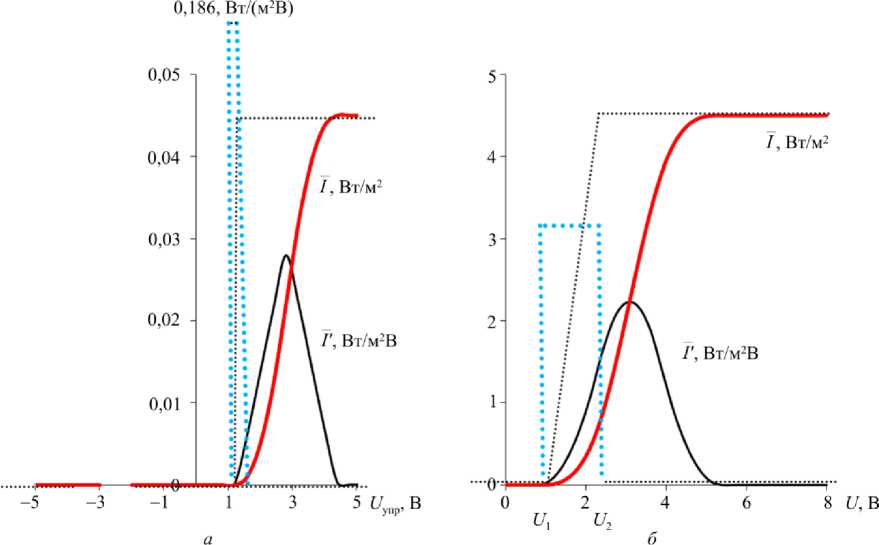
Рис. 4. Рассчитанная функция свечения I из оптоволокна и производная I' для диагностирования давления на локальном участке ( а ) и по всей длине ( б ) датчика

Fig. 4. The calculated function of luminescence I from optical fiber and derivative I' for diagnosing of pressure on the local segment ( а ) and along the whole length ( b ) of the sensor

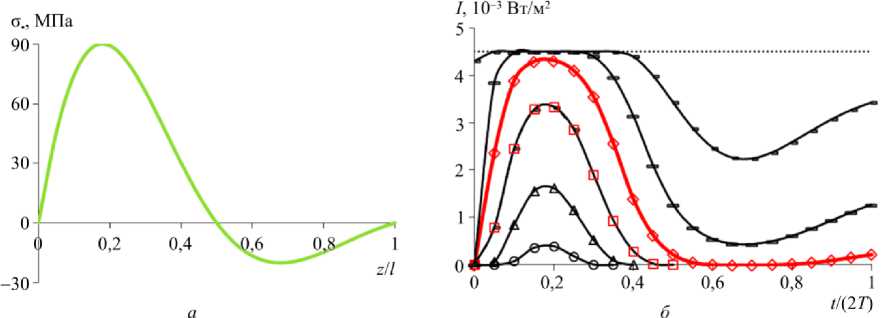
Рис. 5. Распределение давления а . ( z ) ( а ) и функция свечения I из оптоволокна для различных величин U _упр1 электрического импульса сканирования ( б ) Fig. 5. Distribution of pressure а . ( z ) ( а ) and luminescence function I from

the optical fiber for various values U _упр1 of an electric impulse of scanning ( b )

Для неоднородного распределения давления а . ( z ) (рис. 5, а ) были решены прямая (11) и обратная (12), (13) задачи для заданной на рис. 2 функции I ( U ) свечения, где время T = 1 / c прохождения импульсом всей длины 1 = 1м датчика со скоростью c = 3 - 10 8 м/с, ширина импульса 1 1 = 1 мм, начальный момент времени t = 0 соответствует моменту входа импульса в датчик, момент выхода t света из световода. В прямой задаче найдены (рис. 5, б ) функции свечения I ( t ) на выходе из оптоволокна для различных численных значений:

U упр1 = 1,576В (о), 2,241В (А), 2,907В (□), 3,572В (◊), 4,244 В ( □), 5,106 В (а) электрического импульса сканирования; предел насыщенного свечения наступает при значении U _упр1 = 6,658 В (пунктирная линия). В обратной задаче найдено распределение давления а . ( z ) (см. рис. 5, а ) по значениям функции интенсивности свечения I ( t ), в частности для значения управляющего напряжения U _упр1 = 3,572 В (◊), для которого отсутствуют «неинформативные зоны» из участков с «нулевыми» ( I = 0 ) и «насыщенными»

( I = c ₁ I _max) значениями интенсивности свечения I ( t ) (см. рис. 5, б ), где относительная ширина импульса c ₁ = l ₁/ l . Отметим, что если для некоторого значения U _упр1 есть неинформативные зоны для функции интенсивности свечения I ( t ), то необходимо дополнительно провести измерения I ( t )для другого значения U _упр1 уже с информативными участками в этих зонах, в частности взаимодополняющие графики (□), ( ) на рис. 5, б . Таким образом, сканирование неоднородного давления σ_• ( z ) предельно узким видеоимпульсом позволяет получить аналитическое решение (12), что значительно упрощает известный алгоритм [29] обработки светового сигнала на выходе из оптоволокна.

Заключение

Разработаны алгоритм и математическая модель локации неоднородностей давления по длине l оптоволоконного пьезоэлектролюминесцентного датчика с использованием локационного сканирующего электрического видеоимпульса U ₁ с пошаговым изменением величины импульса U ₁ на каждом цикле прохождения исследуемого локального участка l ₁ ⊂ l . Показано, что расчет функции плотности f 1 _• ( ζ ) распределения давления σ 1 _• на локальном участке внешней боковой цилиндрической поверхности оптоволоконного датчика по результатам замеряемой на торцевом сечении датчика интенсивности света из оптоволоконной фазы для случая нелинейной зависимости I = I ( U ) интенсивности света I от действующего на электролюминесцентный элемент напряжения U (см. рис. 2) сводится к решению интегрального уравнения Фредгольма 1-го рода (5) с разностным ядром K ( x - s ) (6), зависящим от передаточных коэффициентов a ₁ , a ₁ датчика, относительной длины l ₁ / l исследуемого локального участка l ₁ и производной I '( U ) (см. рис. 2) заданной функции свечения электролюминесцентного элемента.