Математическая модель индуктивной измерительной ячейки для бесконтактной кондуктометрии

Часто во многих отраслях промышленности и в лабораторной практике возникает необходимость контролировать концентрацию электролитов в растворах в режиме реального времени. Весьма, удобным методом для решения этой задачи является кондуктометрия. Однако область применения традиционных контактных кондуктометров ограничена, коррозией электродов. Обойти это ограничение можно, используя бесконтактные датчики электропроводности. При работе с водными растворами целесообразно использовать частоты от десятков герц до десяти мегагерц. В указанной области частот для бесконтактной регистрации электропроводности используют три основных типа датчиков (трансформаторные, емкостные и индуктивные ячейки) и их комбинации. Данная работа связана с исследованием индуктивной ячейки. Индуктивная ячейка представляет собой катушку индуктивности, намотанную на. трубку из диэлектрика. Исследуемый образец помещается внутрь трубки. Считается, что подобные датчики могут быть эффективны лишь при работе с сильно проводящими образцами (различные металлы). В этом случае импеданс катушки изменяется при внесении в нее образца, из-за. токов Фуко. Данный режим работы датчика, исследован достаточно хорошо, существуют формулы, позволяющие связать импеданс датчика, с удельной электропроводностью образца. [1, 2]. При работе со слабо проводящими образцами, такими как водные растворы различных электролитов, токи Фуко не могут существенно изменить импеданс датчика, поэтому индуктивные датчики обычно не используются при работе с растворами. У индуктивных ячеек есть еще один недостаток: существует паразитная емкость между обмоткой и исследуемым образцом, причем, в книге М.В. Кулакова [1] отмечалось, что емкость вносит искажения лишь при работе с образцами, обладающими достаточно низкой электропроводностью. Для устранения влияния этой паразитной емкости на результат измерений используют специальные экраны, которые, являясь проводниками, могут существенно ухудшить чувствительность кондуктометра. Существование емкости между катушкой и образцом позволяет использовать индуктивные ячейки для измерения электропроводности слабо проводящих образцов. Но для успешного применения индуктивных ячеек необходимо уметь количественно описывать эффекты, связанные с емкостью образец-катушка, требуются математические модели. В монографии Б.А. Лопатина [2] и обзоре [3] приведены различные эквивалентные схемы индуктивной ячейки, в том числе и с учетом емкости катушка-образец. Однако все они отличаются некоторой искусственностью, для определения численных значений эквивалентных параметров требуется проводить измерения с уже изготовленной ячейкой. Удовлетворительная модель, учитывающая паразитную емкость образец-катушка и позволяющая теоретически оценить эквивалентные параметры, так и не была построена.

Целью данной работы является разработка простой для понимания эквивалентной схемы и математической модели индуктивной ячейки, которые позволили бы описать влияние емкости образец-катушка на импеданс датчика, и последующая экспериментальная проверка теоретических выводов. Результатом построения математической модели должна стать максимально простая формула, позволяющая рассчитать импеданс индуктивного датчика в зависимости от электропроводности образца, геометрических параметров и свойств материалов, из которых изготовлен датчик, без привлечения численных методов решения дифференциальных уравнений в частных производных.

2.    Теоретическая часть

Рассмотрим процессы, происходящие внутри индуктивной ячейки, если в нее помещен изотропный проводящий образец. Катушку будем считать достаточно длинной, чтобы можно было пренебречь краевыми эффектами.

Электрическое поле внутри катушки связано не только с наличием переменного магнитного поля. Предположим, что частота питающего напряжения настолько мала, что индуктивностью можно пренебречь, а в каждый момент времени электрическое поле считать постоянным. У электрического поля есть составляющая, направленная вдоль оси катушки, связанная с тем, что к катушке подключен источник напряжения. Соответственно, вдоль витков катушки имеется распределение потенциала, каждый следующий виток имеет потенциал, отличный от потенциала предыдущего витка. Следовательно, в пространстве внутри катушки и вне катушки есть электрическое поле, некоторое распределение потенциала. Именно эта составляющая электрического поля связана с паразитной емкостью образец-катушка.

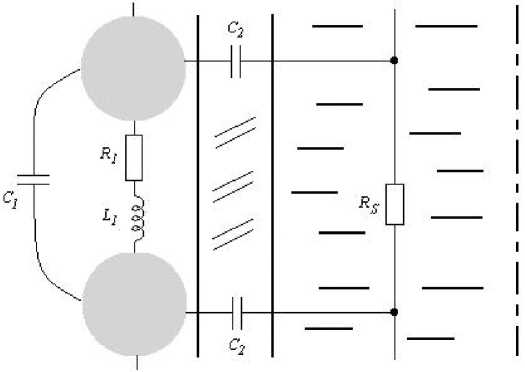
Рис. 1. Схема, иллюстрирующая физический смысл эквивалентных параметров (рисунок не в масштабе). Представлены два. соседних витка, (пояснения в тексте)

Будем считать катушку системой с сосредоточенными параметрами (рис. 1; рис. 2а). Рассматриваем однослойную катушку, намотанную виток к витку, наклон витков минимально возможный, толщина, стенки измерительной ячейки велика, по сравнению с дна- метром провода. Будем считать, что потенциал вдоль одного витка неизменен, а от витка к витку меняется скачком, причем витки имеют нулевой наклон.

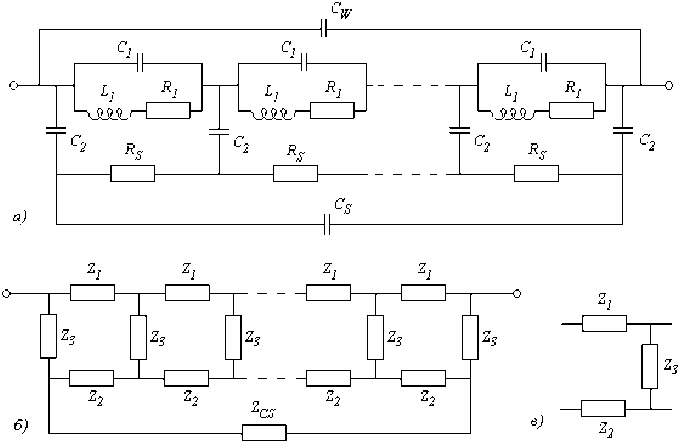
Рис. 2. Эквивалентная схема, индуктивной ячейки (пояснения в тексте): а) — полный вариант эквивалентной схемы, б) — схема, использовавшаяся при расчете импеданса, катушки с образцом, в) — повторяющийся элемент схемы

Токи в образце влияют на. распределение тока, в витках через перезарядку емкости виток-образец ( C₂\ Перезарядка происходит благодаря наличию радиальной составляющей электрического поля (компонента, направленная вдоль оси катушки, рассматривается отдельно ниже). Так как диаметр провода много меньше толщины стенки, искажением силовых линий электрического поля вблизи витков пренебрегаем. Поэтому емкость виток-образец будем оценивать как емкость цилиндрического конденсатора, образованного витком и внутренней поверхностью ячейки, длина, конденсатора, равна, диаметру провода:

C2 = 2тте0е^/ ln (1 + h/R), где d — диаметр провода, Ei — относительная диэлектрическая проницаемость материала стенки, h — толщина стенки, R — внутренний радиус ячейки. В большинстве случаев h ^ R. тогда C2 ~ 2^EoEiRd/h. Число емкостей C2 равно числу витков N.

Межвитковую емкость (Ci), не связанную с образцом, оценим как емкость двух параллельных цилиндров длиной, равной окружности витка. Влияние материала, стенки ячейки не учитываем, так как в большинстве случаев его относительная диэлектрическая проницаемость не будет превышать 10, пренебрегаем влиянием материала изоляции провода. Для цилиндров одинакового радиуса, получим

C_i = 2 ^ ² Re ₂ e ₀

1 -

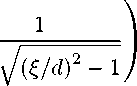
где E2 — относительная диэлектрическая npoiшпаемость среды, окружающей витки. £ — расстояние между осями цилиндров. Так как рассматривается катушка, намотанная виток к витку, £ = d + 8 (8 — кратчайшее расстояние между поверхностями цилиндров, удвоенная толщина изоляции провода), при 8 ^ d получим Ci ~ 2T²RE2Eo-^2|".

Эффективную индуктивность (Li) и омическое сопротивление витка (Ri) можно легко оценить. При отсутствии образца в ячейке элементы Rs и Cs, отражающие свойства образца, следует заменить разрывом. При этом емкость виток-образец (С2) также следует исключить из рассмотрения. Тогда импеданс катушки будет равен импедансу цепи, составленной из (N — 1) последовательно соединенных элементов Zi. Откуда следует, что эффективные индуктивность и омическое сопротивление витков — просто уменьшенные в (N — 1) раз индуктивность и омическое сопротивление пустой катушки. Эти параметры легко найти по стандартным формулам или же их можно измерить для уже изготовленной катушки при отсутствии образца. Емкость С2 также можно измерить напрямую с помощью прибора. Сделать это можно так: помещаем в катушку цилиндр из фольги, добиваемся его плотного прилегания к стенкам ячейки, подключаем оба вывода катушки к одному разъему прибора, а фольгу ко второму. Прибор покажет суммарную емкость виток-образец для всех витков. С2 будет в N раз меньше.

Емкость С1 также можно измерить непосредственно, разместив вплотную друг к другу на внешней поверхности ячейки два кольца из провода, из которого изготовлена катушка. Емкость между этими кольцами и будет С1.

Пренебрегая искажениями поля, связанными с формой витков (диаметр провода много меньше толщины стенки), будем считать, что вдоль боковой поверхности образца потенциал изменяется линейно. Краевыми эффектами пренебрегаем. Тогда распределение поля в образце такое же, как и в обычном прямом проводе: напряженность электрического поля направлена вдоль оси катушки, от радиуса не зависит. Емкость, образованную «торцами» образца (Сд), оценим как емкость плоского конденсатора, образованного торцами катушки (с учетом диэлектрической проницаемости образца):

Сд = едeo^R2Д где ед — относительная диэлектринеская проницаемость образца, I — длина катушки. Сопротивление образца (Rs) оценим как сопротивление прямого провода, материал которого обладает удельной электропроводностью ст:

Rs = d/ ( ct^R ² ) .

С ростом частоты из-за скин-эффекта эффективное значение Rs будет увеличиваться, a Li уменьшаться. Эти поправки легко учесть, если пренебречь краевыми эффектами, что и будет сделано ниже.

Запишем уравнения Максвелла и материальные уравнения и определим распределение магнитного поля по радиусу катушки, пренебрегая краевыми эффектами (все вычисления производятся в системе СИ). Систему уравнений можно свести к уравнению относительно поля Н. Переходя к комплексной записи, для аксиально-симметричной задачи в цилиндри ческих координатах получим (аналогичная задача решена в книге А.Н. Тихонова и А.А.

Самарского [4]):

лгу- + 1 дН + (-гшстццо — ед еоццо(гш)2)Н = 0, dr т yr где г2 = —1, ц — магнитная проницаемость образца.

Данное уравнение сводится к уравнению Бесселя нулевого порядка заменой переменных ж = тл/А. где А = —гшстццо — ед еоццо(гш)².

Общее решение данного уравнения:

Н (rVA) = bJ₀(rVA) + cY₀(rVA).

Из условия конечности поля на оси цилиндра: c = 0.

Константу b найдем из граничного условия: поле внутри катушки вне образца соответствует полю идеального соленоида:

к    Шо b =             ,

Uo ( rVA )

где N — число витков катушки, I — длина катушки, R — внутренний радиус катушки, I = Т"ое^гш<; — ток через катушку.

Таким образом, Н^t) = ^(r^.

Далее, зная магнитное поле внутри катушки, можно найти мгновенный магнитный поток через витки катушки Ф, а затем индуктивность L катушки с образцом:

\                 2ttN 2I ^ RJ п, \ ■ '

^ф^^t) = N J_g²„_№°^Н(r, ^t)d^r =---- ^(R^----

_ Ф(t) _ 2^N ²_№oRJi ( RVA )

= Ж =    I V AJo ( R V A )  ■

Данное соотношение справедливо и для сильно, и для слабо проводящих образцов. Записанная таким образом индуктивность описывает и связанное со скин-эффектом изменение потока через катушку (поправки к действительной части), и дополнительные омические потери в образце (мнимая часть).

При рассмотрении слабо проводящих немагнитных образцов (при | r V A | ^ 1) функции Бесселя можно разложить в ряд до 2-го порядка, получим

2^N ²_WoRJi(RVA) _ ^N²woR² • 2 Ji ( rVA) _     2 Ji ( rVA )

I V AJo ( r V A )   = I • R V AJo ( r V A )   = ^O r V AJo(r V A)

Lo

(1 -

iwR²CT^^o 8

) ’

где Lo — индуктивность пустой катушки.

Если затем рассмотреть импеданс катушки с образцом (без учета емкости виток-образец), получим

■ т - V • Т , R‘2^‘2CT^^0L0

Z — Ro + %wL — Ro + iwLo +--------, где Ro — омическое сопротивление витков катушки.

Данную поправку к действительной части импеданса можно получить из энергетических соображений, не используя функций Бесселя. Для этого нужно рассмотреть изменение добротности при внесении образца в катушку в предположении, что магнитное поле внутри катушки при этом остается однородным, а дополнительные потери связаны с нагревом образца токами Фуко.

Аналогично рассмотрению индуктивности катушки, учитывая отсутствие объемных зарядов в образце, для осевой составляющей напряженности электрического поля получим

Е ( г ) =

и Jo (rVA) а • Jo (rVa) , где U — напряжение между двумя соседними витками.

Так как для рассматриваемой задачи важно напряжение между различными участками поверхности цилиндра, то для определения Rs в качестве напряжения будем использовать именно напряжение, «измеренное» на поверхности цилиндра. Суммарный ток легко найти, U-kR²^2Ji(rVa)

зная распределение электрического поля по радиусу: I = ^ r^j ( rVa ) ' Наконец,

Rs = U

a r V ajo Rr V a ^ i

^^R2   2 Ji RrA}  °

При   \rVa\     ^    1 можно воспользоваться приближенной формулой rs « 411 (1 + w^2 \ ° ^R2 ст8

Эквивалентная схема катушки построена, эквивалентные параметры приведены ниже:

e ° e o tR ²        d ^rV AJ° ^RRVA^ 1

C s =----;----, Rs =  ,,2------7---—\--, C1 « 2tt Re2eo\—,

1          tR   2Ji (rVA)  ° r e e Rd T - L0     2J1(Ra/A)       _ Ro          .2

^c2 ~ 27^ 1 _h^,L1 (_N _ 1) r ^V Aj _o (r ^V A) , ^R1 N — 1 ^,A °    ^EsE—^E-' .

При работе с водными немагнитными растворами в качестве исследуемых образцов на ^r / A^J o ( ^r / A )      ^{2 J} i ( ^r / A )

частотах до 10 Ml ц и R <  1 см, можно считать, что _2/ (д^д) ~ //АJ ( R^A ) ~ 1' ^^ными словами, можно пренебречь скин-эффектом и токами Фуко в образце.

Полный импеданс между выводами катушки (рис. 26) легко определить, записав законы Кирхгофа для элементарной ячейки, образованной импедансами Z1, Z2, Z3 (рис. 2в). Полученную систему можно свести к рекуррентному (возвратному) уравнению относительно одного из узловых потенциалов. Методы решения подобных уравнений известны (подобная задача о нахождении импеданса решена, например, в книге Бутикова Е.И. и др. [5]). Выполнив ряд арифметических преобразований, получим импеданс катушки:

^(| ’ — ^х) ( ^Ау — V) + х ( ^аУ' ¹ — Д' ¹ + А 2 — д) («7 ^— z) (^{лу — Ау}) ⁺ z (^{АуУ 1 — а У 1 + Л} 2 ^{— А} 1 )

где введены обозначения:

^Z 1 ^{+ Z} 2 _д            -w^cs      ^{2 [Z}cs^Z 1 ^{+ (N —} 1) ^Z 2 ^(Z 1 ^{+ Z} 2 ^)]

° = z ' = ^{— (N —11}   ’ ^х =------------ Z2------------

• ⁷ = ^— z (1 2 (^{N —1 +} Z; )⁺ Z; )-^А1Д = ^{1 +} «( 1 ± У1+1).

Данные соотношения справедливы при « = 0, других ограничений на импедансы Z 1, Z2, Z3, Z_cs нет. В данной задаче

- ^{R1 +} '^ ■               7.- ¹    7 -   ¹

• ¹   (R1 + iwL1) гшС1 + 1,   ²     °, ³   гшС2, ^cs   гшС°^.

3.    Экспериментальная часть

Метод, использованный при выводе формулы для Z, справедлив при N > 4. Однако проверка частных случаев N = 4, N = 3 и N = 2 подтверждает справедливость формулы и при N > 2. Возможны и другие формы записи данного соотношения. Все они эквивалентны. Приведенная выше форма, по мнению автора, более остальных удобна при рассмотрении различных предельных случаев и введении малых параметров. В дальнейших расчетах, выполненных с помощью ЭВМ, используется данная формула без каких-либо упрощений.

Помимо элементов эквивалентной схемы, введенных выше, катушка может обладать еще одним: паразитной емкостью провода или других соединительных элементов, исполь зуемых для подключения катушки к остальным деталям кондуктометра. Данный параметр может оказаться весьма важным. Для его описания введем в эквивалентную цепь еще один конденсатор Сщ, подключенный параллельно катушке. Тогда окончательно импеданс ячей ки будет записан так: Ztr z 1+i^CwZ'

Если при исследовании электропроводности растворов возникает необходимость учесть эффекты, связанные с экранировкой электрического поля свободными зарядами раствора и их диффузией, к R° следует присоединить соответствующую концентрационно-зависимую эквивалентную емкость, как предлагается, например, в монографии Б.А. Лопатина [2]. Величина емкости может быть оценена с помощью известных электрохимических методик.

Наибольший практический интерес представляет кондуктометрия немагнитных растворов, поэтому для проверки математической модели в качестве образца использовался водный раствор NaCl.

Чтобы зафиксировать изменение импеданса ячейки при внесении образца, была использована схема, представленная на рис. За.

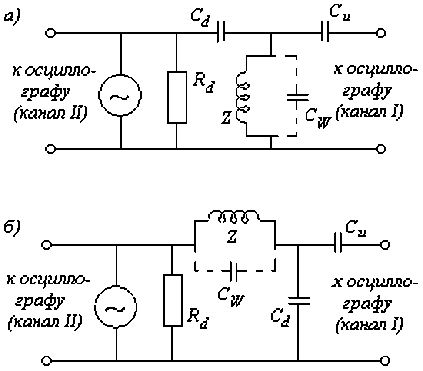
Рис. 3. Схема, экспериментальной установки: а) — вариант для работы с растворами, б) — вариант для измерения Cw

Схема, была, собрана, на. макетной плате WBU-506 фирмы Wisher Enterprise (Тайвань). Металлическое основание платы соединялось с общим выводом (землей) генератора, и осциллографа. Регистрировалась амплитуда, сигнала, на. входе и выходе делителя, образованного катушкой и конденсатором С д. Конденсатор С_и использован, чтобы уменьшить влияние входного импеданса, осциллографа. Использовался двухканальный компьютерный осциллограф PCSGU250 фирмы Velleman (Бельгия). Резистор Кд служит в качестве дополнительной нагрузки, необходимость его применения связана, с особенностями использованного генератора. ВЧ (Г4-154, ГП «Нижегородский завод им. М.В. Фрунзе», Россия). На рис. 36 представлена схема, использованная для измерения Сщ.

Процедура измерения Сщ состоит в определении частоты сигнала, при которой на выходе делителя наблюдается минимальное значение амплитуды, измерение проводится при отсутствии образца в ячейке. Частота, соответствующая минимуму выходного сигнала, является резонансной для LC-кoнтypa, образованного паразитной емкостью Сщ и индуктивностью Lo. Зная частоту и индуктивность, легко оцениваем Сщ. Если по какой-либо причине точность измерения Сщ окажется неудовлетворительной, можно перед каждым измерением с участием раствора, определять модуль передаточной функции делителя (т.е. отношение амплитуд сигналов на выходе и входе делителя). Затем, зная номиналы всех остальных элементов схемы, можно вычислить Сщ. Однако удобнее совместить оба способа и работать так. Сначала по минимуму сигнала определяем диапазон величин, в который попадает Сщ, потом перебором величин из этого диапазона находим то значение, при котором расхождение расчетного и измеренного значения модуля передаточной функции не превышало бы 5 %.

Измерения с растворами проводились следующим образом: измерялся модуль передаточной функции делителя (рис. За) при различных частотах и различных концентрациях NaCl в водном растворе. Измерения были проведены с применением двух различных измерительных ячеек, ячейки были близки по всем параметрам, кроме величины емкости виток-образец (С2). Для ячейки I емкость виток-образец равнялась 0.5 пФ, для ячейки II — 1.5 пФ. Обе ячейки были изготовлены из стандартных стеклянных пробирок. На внешнюю сторону пробирок была, намотана, катушка, использовался медный провод диаметром

• (d) 0.4 мм, изоляция — лак. Края катушки фиксировались клеем «Момент 88» (Henkel). Катушка располагалась в средней части пробирки.

Передаточную функцию делителя ( к) легко рассчитать, зная Z_tr. Стоит отметить, что в силу довольно большой емкости коаксиального кабеля, соединяющего устройство и осциллограф, регистрируемое осциллографом напряжение и напряжение на выходе делителя существенно отличаются, что учтено в формуле (первая дробь):

к       Zosc

^(Zosc + ^Z Cu^

_____________ (Zosc + Z cu ) Zt_T _____________

[(Zosc + ZCu) ZtT + ZCd (Zosc + ZCu + Ztr)] ’ где Zcu и Zed ~ импедансы соответствующих конденсаторов, Zosc — входной импеданс I канала осциллографа, включая импеданс коаксиального кабеля.

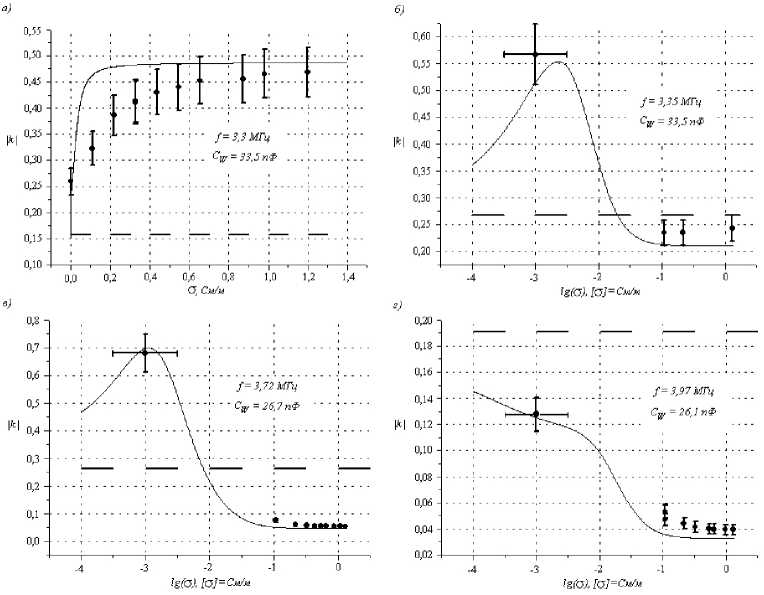
Рис. 4. Рассчитанные (сплошная кривая) и полученные экспериментально (точки) зависимости модуля передаточной функции делителя (к) от электропроводности образца при различных частотах и параметрах измерительной ячейки (пунктиром показана, полученная экспериментально величина. модуля передаточной функции при отсутствии образца, в ячейке): а), б) — ячейка. I, в), г) — ячейка. II.

Значения удельной электропроводности растворов при заданной концентрации с учетом температурных поправок были вычислены по данным справочника. [6]. Относительная диэлектрическая и магнитная проницаемости для водных растворов NaCI крайне мало изменяются при изменении концентрации, их можно считать постоянными ( ед _ 80, ц _ 1).

Частоты, на. которых проводились измерения, выбирались так, чтобы, с одной стороны, они были близки к резонансной для LC-контура, образованного катушкой и паразитной емкостью Cw, ^что позволяло получить значительные различия в амплитуде выходного сигнала. при различных значениях проводимости. С другой стороны, по мере приближения к резонансу возрастают требования к точности измерения всех параметров схемы. Поэтому не использовались частоты слишком близкие к резонансной (работа, проводилась на. частотах, отличающихся от резонансной на 5 — 10 %).

В зависимости от выбора, частоты и параметров измерительной ячейки (главным образом, от величины C2) зависимость модуля передаточной функции делителя от элек- тропроводности раствора может иметь максимум, быть возрастающей или убывающей. Полученные в эксперименте зависимости и расчетные кривые приведены на рис. 4.

Помимо схемы на основе делителя использовались две конструкции на основе автогенератора (рис. 5). Изменение электропроводности раствора регистрировалось по изменению частоты сигнала автогенератора. Измерительная ячейка ( Z_tr) является частью колебательного контура.

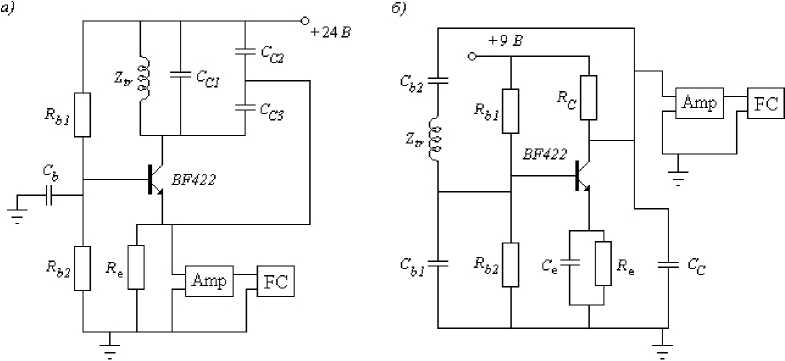
Рис. 5. Схемы автогенераторов: а) — с использованием параллельного резонанса, б) — с использованием последовательного резонанса. Amp — промежуточный усилитель, ЕС — частотомер

Использовались две несколько различающиеся схемы автогенератора. В одной использован последовательный резонанс, в другой — параллельный. В устройстве с параллельным резонансом использовалась ячейка I, в устройстве с последовательным резонансом — ячейка II. Однокаскадный промежуточный усилитель был собран автором по стандартной схеме. В качестве частотомера использовался мультиметр UT70B фирмы Uni-Trend (Китай).

Можно показать, что для схем, представленных на рис. 5, петлевое усиление ( КР) может быть выражено в следующем виде:

КР = (i+szC3) (% + zC1 + ^f1 + SZC3 + zC3 + zC2) - для Устройства, преястав- ленного на рис. 5а,

R2- + Ra) — ^ля устройства, представлен-

К8=   ^1+szi (1 + ^2 Z2 )(1 + -^2

1+SZ1-SZ2 1 + zCc + Rc 1 + zCbi + ного на рис. 56. Здесь Zci, Zc2, Zc3, Zcc, Zcbi ~ импедансы соответствующих конденса

Re     7   1+*wCb2Ztr

1+iwC_eR_e • ^Z2 =    гшС _Ь2

торов. S — средняя крутизна транзистора. Z₁ =

*

При выводе формул для расчета петлевого усиления предполагалось, что транзистор — безынерционный элемент (т.е. параметр S — чисто действительный). В данном случае средняя крутизна определялась на частоте 1 МГц как отношение амплитуды первой гармоники тока коллектора к амплитуде переменной составляющей напряжения база-эмиттер. Частота сигнала автогенератора соответствует частоте, при которой аргумент петлевого усиления равен нулю.

Приведенные выше формулы для расчета петлевого усиления не учитывают паразитные индуктивности и емкости радиодеталей. Поэтому перед работой с растворами проверялось соответствие измеренных и рассчитанных (с помощью формул для петлевого усиления) частот. Для устройства с параллельным резонансом различие оказалось несущественным (менее 0.25 МГц), для устройства с последовательным резонансом частоты отличались на 1.2 МГц. Важно отметить, что чем выше частота, тем сильнее отклик импеданса ячейки на изменение электропроводности образца (рис. 6). Поэтому при существенном различии рассчитанных и измеренных экспериментально исходных (без образца в ячейке) частот автоколебаний можно ожидать лишь качественное совпадение реальных и рассчитанных зависимостей частоты сигнала автогенератора от электропроводности образца, размах же изменений частоты может сильно различаться. Однако этот факт не является ограничением для использования математической модели индуктивной ячейки.

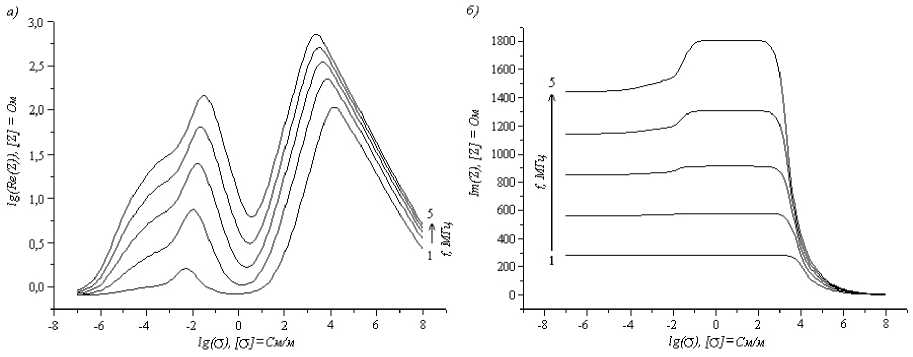
Рис. 6. Рассчитанная зависимость импеданса, катушки с образцом от электропроводности образца: а) — действительная часть, б) — мнимая часть

В большинстве практически значимых случаев изменение импеданса ячейки при изменении электропроводности образца, является малой поправкой к импедансу. Причем, эта. малая поправка, не зависит от паразитных параметров радиодеталей или нелинейности транзистора. Поэтому, если обеспечить совпадение рассчитанных и измеренных исходных частот автоколебаний (вручную подстраивая частоту собранного генератора, или изменяя используемые в расчете величины параметров, задающих частоту), можно ожидать не только качественное, но и количественное совпадение рассчитанных и измеренных экспериментально кривых частота-электропроводность.

Для устройства, с последовательным резонансом частотозадающими элементами являются измерительная ячейка и конденсатор Си, параметры конденсатора не зависят от свойств раствора. Вместо реальной величины емкости данного конденсатора при расчете можно использовать эффективную величину, которая обеспечит совпадение исходных частот не хуже 0.25 МГц, а. затем при расчете кривой частота-электропроводность использовать уже эффективное значение, что и было сделано. Для устройства с параллельным резонансом при расчете использовались реальные величины параметров (измеренные непосредственно, либо заявленные производителем).

Расчетные и экспериментальные зависимости частоты сигнала, автогенератора, от электропроводности раствора, приведены ниже (рис. 7).

При создании частотного кондуктометра, аналогичного описанным выше, следует особое внимание обратить на следующий факт. При увеличении С2 чувствительность резко возрастает, особенно в области малых проводимостей (0.01-0.1 См/м). Но при увеличении чувствительности проявляется неприятный эффект: если взять ячейку, обладающую достаточно большой величиной С2, возможен срыв колебаний в области малых проводимостей. Данный эффект удается описать в терминах предложенной эквивалентной схемы. На рис. 7 также приведены модули петлевого усиления. Видим, что при уменьшении электропроводности образца, для устройства, с последовательным резонансом модуль петлевого усиления резко падает, для устройства, с параллельным резонансом имеется локальный минимум. В данной области при достаточно больших величинах С2 возможен срыв колебаний — нарушится условие баланса амплитуд. Можно показать, что чем больше величина С2, тем сильнее уменьшается модуль петлевого усиления.

На графиках (рис. 7) модуль петлевого усиления заметно больше 1, это связано с тем, что характеристики транзистора, аппроксимируются линейной зависимостью, у реального транзистора, по мере возрастания амплитуды входного сигнала, (напряжения база-эмиттер) величина параметра S уменьшается до тех пор, пока модуль петлевого усиления не будет равен 1. При работе в линейном приближении условие строгого равенства для модуля петлевого усиления нужно заменить на неравенство. Автоколебания будут возбуждаться, если модуль петлевого усиления больше 1.

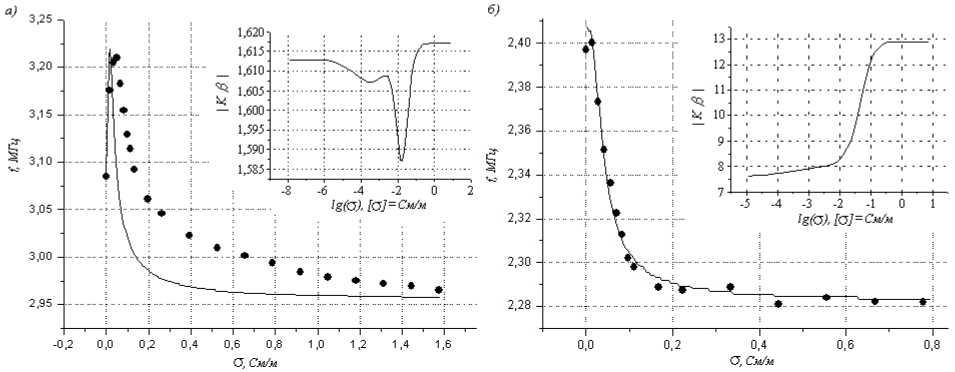
Рис. 7. Расчетная (сплошная кривая) и экспериментальная (точки) зависимости частоты сигнала, автогенератора, от электропроводности образца. Также приведены расчетные зависимости модуля петлевого усиления ( КЗ): а) — схема с параллельным резонансом, б) — схема с последовательным резонансом

В заключение отметим моменты, на. которые стоит обратить особое внимание при проектировании и изготовлении частотного кондуктометра, аналогичного описанным выше. Если предполагается работа с устройством вблизи источников переменных электромагнитных полей, для повышения надежности измерений требуется экранировка, всей установки, экран может изменить характеристики автогенератора. Для индуктивного датчика должно выполняться условие «длинной катушки», чтобы можно было пренебречь краевыми эффектами. Для «короткой катушки» чувствительность может оказаться выше, но данный случай не описывается математической моделью, предложенной в настоящей работе. Чтобы избежать влияния входного импеданса, частотомера, на. работу автогенератора, желательно использовать промежуточный усилитель, обладающий высоким входным сопротивлением и малой входной емкостью.

4.    Выводы

В данной работе предложена, математическая модель, верно описывающая поведение импеданса, индуктивной ячейки при изменении электропроводности исследуемого образца. Модель включает не только эффекты, связанные с емкостью виток-образец, но также учитывает возникновение токов Фуко в образце и связанное с ними изменение магнитного потока, через витки катушки. Уравнения модели могут быть использованы при проектировании кондуктометров для оценки характеристик индуктивной ячейки, позволяют выбрать значения параметров, при которых устройство будет обладать заданными свойствами.

В заключение хочу поблагодарить сотрудника, лаборатории широкодиапазонных уравнений состояния ОИВТ РАН Дмитрия Владимировича. Князева, за. множество ценных советов и активное участие в обсуждении результатов. А также за. помощь в подготовке данной статьи заведующего кафедрой биофизики и экологии МФТИ Эдуарда. Михайловича. Трухана. и заведующего лабораторией физики живых систем ИОФ РАН Александра. Ивановича. Дьяченко.

Работа, поддержана, аналитической ведомственной целевой программой Развитие научного потенциала, высшей школы № 2.1.1/3179.