Математическая модель информационного взаимодействия объектов живой природы с электромагнитными излучениями
Автор: Даровских Станислав Никифорович
Статья в выпуске: 2 (219), 2011 года.
Бесплатный доступ
Описана математическая модель информационного взаимодействия объектов живой природы с электромагнитными излучениями. С ее использованием обоснованы особенности воздействия природного и антропогенного фактора на биоткани живых организмов.
Электромагнитные излучения, живые организмы, модель
Короткий адрес: https://sciup.org/147154731
IDR: 147154731 | УДК: 537.868
Текст научной статьи Математическая модель информационного взаимодействия объектов живой природы с электромагнитными излучениями
Математические модели, описывающие информационное взаимодействие живых организмов с природным электромагнитным фоном, лежат в основе изучения его управляющей роли в поддержании способности биологических систем противостоять изменениям внешней и внутренней среды, сохранять относительное динамическое постоянство своей структуры и свойств. Природный электромагнитный фон, обусловленный космическими и геофизическими факторами, в значительной степени подвергнут искажениям из-за воздействия на него электромагнитных излучений (ЭМИ) антропогенного происхождения. Эти излучения создают новое негативное качество среды обитания для живых организмов на долгую перспективу. В этой связи актуальным является разработка математической модели указанного взаимодействия для рассмотрения особенностей воздействия природного и антропогенного электромагнитного фактора на биоткани живых организмов.
Описание модели
В основу разработки модели положены известные сведения о многообразии дисперсионных свойств живых тканей и резонансных взаимодействий их с электромагнитными излучениями [1]. Они позволяют рассматривать живую ткань как набор из N пространственно разнесенных фильтров (это свойство модели отражает также существование пространственной дисперсии в отношении внешнего ЭМИ), каждый из которых оптимально согласован с отдельными частотно-временными характеристиками внешнего ЭМИ. Такая модель живой ткани (фильтровая модель) позволит рассмотреть особенности пространственного распределения в ней поглощенной энергии ЭМИ как антропогенного, так и природного происхождения, а также сделать ряд предположений о возможности ряда физических процессов, непосредственно связанных с результатом взаимодействия ЭМИ с тканями живого организма. Так как патологические процессы в живых организмах носят, как правило, очаговый характер на разных уровнях организации (молекула, клетка, орган и т. д.), то наибольший интерес представляет рассмотрение условий и свойств локального распределения поглощаемой энергии по всему объему живой ткани.
Задача оценки особенностей раздельного распределения поглощаемой энергии в живой ткани может быть сведена к задаче разрешения двух сигналов с близкими координатами областей их поглощения.
В рамках рассматриваемой модели акту поглощения ЭМИ будет соответствовать отклик на выходе соответствующего фильтра с пространст-
Даровских Станислав Никифорович канд. техн, наук, доцент кафедры радиотехнических систем ЮУрГУ; daro v@chel .surnet. ru
венными координатами, согласованного с параметрами падающего на живую ткань электромагнитного излучения.
В качестве критерия меры пространственноволнового различия сигналов используем критерий максимума интеграла квадрата разности s2 двух сигналов i, (г,...) и хД1,...у, являющихся функциями времени t и других параметров [2], е2 = max j |s,(f,r-?;,A+A;)-5y(t,r-^,A+A:y^ (1)
где г (х, у, z) - радиус-вектор, задающий в декартовой системе координат направление распространения сигналов в живой ткани; А(^, ку, к^ - волновой вектор, характеризующий в декартовой системе координат изменение волновых чисел кх, ку, к.; г, (х„ у„ z^, г, (xj, у,, Zj) - радиус-векторы, определяющие положение сигналов s, и Sj в декартовой системе координат соответственно; к, (кх , kw к,), ку (кх, ку, к.) - волновые векторы сигналов $,- и s, соответственно.
В теории сигналов доказывается [3], что максимум интеграла вида (1) имеет место при минимуме интеграла, представляющего собой корреляционную функцию двух сигналов2 s(?,...) и л* (/,...) : \p5=min j s{t,r-rc,k+kcys* {t,r-r^,k+k^dr , (2)
где гс, Гф - радиус-векторы, определяющие положение сигнала s и согласованного с ним фильтра в декартовой системе координат соответственно; кт £ф - волновые вектора сигнала s и его настройки в фильтре соответственно.
Для преобразования соотношения (2) воспользуемся следующим выражением для сигнала, распространяющегося в живой ткани [4]: ^,...) = S(r-rJexpj[ar4A + £j(r-^ (3)
где о - вектор круговой частоты сигнала; S(r-rc) - комплексная амплитуда сигнала, в записи которой учитываются все виды возможной модуляции 5(г-г^=4(г-г^ехр[7фДг-гс)], (4)
где функция ^(г-гс) описывает амплитудную модуляцию сигнала, a tpv (г - гс) - фазовую и частотную модуляции.
В общем случае фильтр согласуется с некоторым опорным сигналом, эквивалентным принимаемому. Он записывается аналогично выражению (3), но отличается от него введением вектора гф вместо вектора гс и вектора кф вместо вектора кс. Указан- ные изменения отражают собственные настройки фильтра. С учетом сказанного выражение для опорного сигнала будет иметь вид
5ф(г,...) = 5(г-Гф)ехру[щГ-(£ + ^ . (5)
Корреляционная функция (2), пропорциональная выходному сигналу согласованного фильтра, может быть записана (с учетом выражений 3 и 5) в виде
У
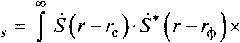
хехру[(£ + £ф)(г-гф)-(£ + ^(г--гс)рг. (6)
Для упрощения записи выражения (6) введем новые переменные векторных разностей Аг = гс - Гф и Ак = кф - кс. Заменим также переменную интегрирования в (6), введя новую г' = г— гс.
В результате преобразований получаем (опустив штрих в обозначении новой переменной /)
Vs
| S^ys'^r-Ar^e^^dr
хехр]^к + ксУс-^к + кфУфУ (7)
Обозначим функцию в квадратных скобках (7) как
Ч'^Аг^к^ J З^У^^г-АгУ^ Чг. (8)
Функция 4*s^Ar,Ak^, являющаяся векторным аналогом «функции неопределенности» радиосигнала, описывает пространственную неопределенность Аг в распределении зон поглощения ЭМИ живой тканью с учетом наличия неопределенности волнового вектора Ак.
Так выражение для проекции векторной функции неопределенности \ys^Ar,Ak^ на ось х будет иметь вид3
\|/s ^Ах,Ак^ = | S(х)-S* (х- Ах^е^ Xdx . (9)
Полученное выражение (9) может быть использовано для определения физических особенностей взаимодействия живых тканей с ЭМИ как антропогенного, так и природного происхождения.
В качестве примера использования разработанной модели для оценки особенностей взаимодействия живых организмов с ЭМИ как природного, так и антропогенного происхождения можно
Математическая модель информационного взаимодействия объектов живой природы с электромагнитными излучениями
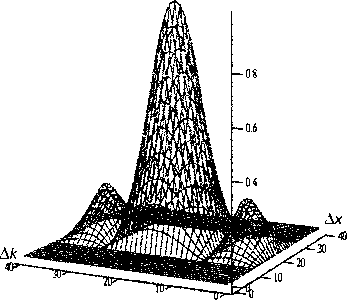
Рис. 1. Вид функции неопределенности для модели антропогенного ЭМИ
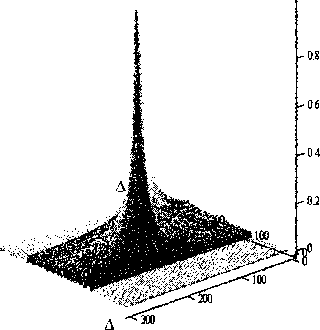
Рис. 2. Вид функции неопределенности для модели природного ЭМИ
использовать одиночный цуг с прямоугольной огибающей протяженностью xD:
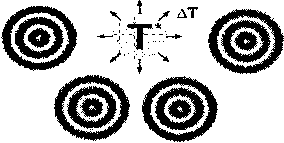
. , \cosAwt-kxY Q s(/,x) = j 4 ’ D (10) [0, при других X. Для ЭМИ антропогенного происхождения частота излучения о в пределах длительности xD волнового процесса (10) является постоянной, а для ЭМИ природного происхождения - она изме няется от одного дискрета xD к другому по закону ю(х) = О)ос'“. При этом общая протяженность волнового процесса XD составляет величину кратную XD,T- eXD=KxD. Использование такой модели является вполне оправданным, так как большинство источников электромагнитного загрязнения окружающей среды используют моночастотные излучения конечной длительности, а ЭМИ природного происхождения представляют собой пульсации различной длительности с разнообразной внутриимпульсной частотной модуляцией. Для выбранной модели ЭМИ антропогенного и природного происхождения получены выражения (11) и (12) их нормированных функций неопределенностей соответственно: % (Ах, ДА)| =- . да L sin — xD l-j—‘ 2 \ xD) , |Дх|<хп; 1 1 " (11) Xk ™ Хтх 2 D 0, |Дх|>Ху. |ф0 (Дх,ДА)| = Вид функций неопределенностей, вычисленных в соответствии с выражениями (11) и (12), изображены на рис. I4 и на рис. 25 соответственно. Из (И), (12) следует, что концентрация поглощенной энергии будет происходить в той области живой ткани, которая наилучшим образом согласована в текущий интервал времени с частотно-временной структурой падающего на неё ЭМИ. При этом если параметры ЭМИ антропогенного происхождения неизменны, а природного -изменяются от импульса к импульсу, то концентрация ЭМИ антропогенного происхождения будет происходить в одной и той же области живой ткани, а ЭМИ природного происхождения - в разных её областях (рис. 3). Источник ЭМИ антропогенного происхождения Источник ЭМИ природного происхождения где b = —г2 4 Функция неопределенности была рассчитана и построена в программе Mathcad И. Значение одного отсчета по оси &х равно 110й м, по оси ДА - 6,283 ■ 109 м"’. Максимум функции неопределенности соответствует точке с координатами отсчетов (20,20). 5 При расчете использовались значения XD = 210*10 м, 6 = 2,8 102°м"1. Фрагмент биоткани живого организма Рис. 3. Пояснение различий в поглощении энергии ЭМИ антропогенного и природного происхождения В условиях ослабленной или малоэффективной системы терморегуляции будет иметь место процесс накопления поглощенной энергии ЭМИ антропогенного происхождения. Последнее будет сопровождаться повышением температуры в этой области живой ткани. Увеличение температуры в живой ткани до значений Т*, превышающих допустимые пределы, является основной причиной нарушения гомеостаза в живом организме со всеми вытекающими из этого негативными последствиями. Эта причина объясняет: почему дети и люди с различными видами психических расстройств наиболее подвержены воздействию ЭМИ антропогенного происхождения даже при низких значениях его интенсивности: у первых - это пока неразвитая система терморегуляции, у вторых - это нарушения в обеспечении межнейронного взаимодействия в осуществлении не только терморегуляции, но и других процессов. Исследование свойств функции неопределенности (12) на примере одиночного цуга, волновые свойства которого характеризуются изменением частоты (с девиацией Асо) в пределах его длительности XD по экспоненциальному закону, указывает на возможность сжатия протяженности волнового процесса в Ксж = Х0 Асо раз. Концентрация энергии, обусловленная резонансными явлениями в среде распространения, приводит при прочих равных условиях к увеличению в Ксж раз объемной плотности энергии волнового процесса. При этом уровни поглощенной энергии этой средой могут быть достаточными для разрыва патологических связей между ферментами и протонами в условии гипоксии клеточных структур. В [5] показана возможность того, что часть энергии рассматриваемых волновых процессов расходуется в местах их концентрации также и на возбуждение упругих колебаний, которые, распространяясь в среде (на рис. 3 они представлены концентрическими окружностями), будут создавать, в случае применения ЭМИ природного происхождения, сложную «картину» «сжатий» и «разрежений» и способствовать тем самым не только усилению теплопередачи от областей с повышенным фоном температуры к близлежащим, но и формированию разветвленной системы гуморальной регуляции в местах их нарушения. Заключение Описанная модель взаимодействия живых организмов с ЭМИ указывает на возможность её использования для синтеза управляющих сигналов для ослабления с помощью специализированных ЭМИ воздействия антропогенного фактора на объекты живой природы.

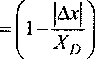
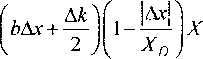
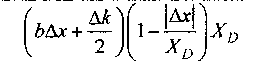
Список литературы Математическая модель информационного взаимодействия объектов живой природы с электромагнитными излучениями
- Самойлов, В. О. Медицинская физика/В.О. Самойлов. -СПб.: Спецлит, 2007. -560 с.
- Дудник, П.И. Авиационные радиолокационные устройства/П.И. Дудник. -М.: ВВИА им. Н.Е. Жуковского, 1976. -514 с.
- Слока, В. К. Вопросы обработки радиолокационных сигналов/В.К. Слока. -М.: Сов. Радио, 1970. -256 с.
- Корн, Г. Справочник по математике для научных работников и инженеров: пер. с англ./под ред. И.Г. Арамановича. -М.: Наука, 1968. -831 с.
- Орир, Дж. Физика: в 2 т./Дж. Орир -М.: Мир, 1981. -622 с.


