Математическая модель излучения частиц Дирака с поверхности эллиптической черной дыры

1. Введение. Одним из самых феноменальных предсказаний из общей теории относительности является существование черных дыр. Черная дыра определяется как область пространства-времени со сверхсильными гравитационными эффектами, и от нее ничто не может вырваться из нее, даже фотоны с их предельной скоростью. Поэтому, если при изучении черных дыр использовать только общую относительности, это приведет к представлению о том, что черные дыры - это «мертвые» термодинамические объекты, т.е. они не имеют температуры или энтропии. Однако в 1970-х годах, используя теорию квантовой механики, Хокинг показал, что черные дыры не такие уж "черные". Черные дыры могут излучать частицы, как излучение черного тела [2, 3].

Расчет температуры черной дыры является актуальной темой, которая широко обсуждается в последнее десятилетие [11, 1, 12, 4, 6].

Однако, в основном расчеты были сосредоточены только на сферических симметричных черных дырах. Примером обсуждения излучения от несферической

черной дыры является излучение от вращающейся черной дыры (черной дыры Керра-Ньюмана) [7].

Однако, работы Уметсу показывают, что расчет температуры в черной дыре Керра-Ньюмана может быть применен только в двумерных задачах [13].

В данной работе рассматривается излучение эллиптической черной дыры. Целью данного исследования было вычислить температуру эллиптической черной дыры, если она излучает частицу Дирака. Метрика, используемая в данном исследовании, ссылается на метрику, предложенную Ни-коураваном (т.е. невращающаяся эллиптическая черная дыра), и она почти схожа с метрикой Рейсса и она почти аналогична метрике Рейсснера-Нордстрема [8, 9].

Для определения температуры был использован комплексный подход, а излучение частиц, которое было проанализировано, являются частицы Дирака. Этот метод является одним из полуклассических методов, и он работает в соответствии с механизмом туннелирования [10]. В этом методе волновая функция определяется в соответствии с этим механизмом, и реше-

ние может быть может быть получено с помощью метода Гамильтона-Якоби. Температура Хокинга может быть рассчитана, если вспомнить соотношение между вероятностью вылетающей частицы со спектром излучения черного тела, которое излучают фермионы.

• 2.    Метод. В данной работе изучается и строиться модель расчета температуры эллиптической черной дыры, если она испускает частицы Дирака. Расчет производился с помощью метода комплексного подхода и аналитической математики.

• 3.    Результаты и обсуждение.

• 3. 1. Обзор эллиптической черной дыры.

В этом разделе приведены результаты и их обсуждения. Сам раздел разделен на несколько подразделов, включая обзор эллиптической черной дыры и процесс испускания частицы Дирака.

Чтобы получить выражение эллиптической метрики, Никоураван использует общую форму статического эллиптического линейного элемента в плоском пространстве-времени Минковского в сферических координатах [8, 9].

Выражение может быть записано как:

ds1

= e2 в (t ’ r) dt2

e ² y ⁽ t , r )

^л r ² + a ² cos² 9

. 2  ,  „2

^—

-(r2 + a2 cos2 9) d92 — (r2 + a 2)sin2 9d^2

где в ( t , Г ) и Y ⁽ t , r ) - неизвестные функции, выражение которых будет определено позже, а a - ось вдоль осей x и оси у.

Зададимся ненулевыми компонентами тензора электромагнитного поля:

F =— Fn = E (r ,9)          (2)

где E ( r , 9 ) - электрическое поле как функция Г,9 :

E (r ,9) =

C

(r2 + a2)sin2 9 + r2 cos 9

где C - константа, зависящая от граничного условия. Согласно расчетам тензора энергии-момента и тензора Риччи, функция отсутствия конвенции в уравнении:

в( t, r) = —/(r) = в( r)            (4)

Таким образом, предполагая a = 0, метрика в уравнении (1) должна свестись к сферически симметричной метрике. В этом случае метрика Рейсснера -Нордстрема, приводится к выражению в виде [8, 9]:

ds s

f 2 M

1 r

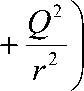
dt2

—

f 1 - 2 M + QT I^{- 1}

f r ² + a ² cos² 6

V

r

^r )

2  ,     2

V r + a )

dr2

- ( r ² + a ² cos² 6 ) d 6 ² - ( r ² + a ²)sin² 6 d^^L

Из приведенной выше метрики следует, что горизонт эллиптической черной дыры, ко-rr торый удовлетворяет условию g — 0 может быть определен как:

r — M ± V M2 + Q2<6)

В данной работе горизонт, расположенный в точке r — ± ia был проигнорирован, так как он пока вызывает сомнения. Тогда обозначив,

2М  О2

P (r) — 1

rr

J (r, 6) — r2 + a2 cos2 6

K (r) — r2 + a2

Приведенная выше метрика может быть записана как

ds ² — P ( r ) dt ² — J ⁽ r ^{, 6 )} dr ² - J ( r , 6 ) de²

V 7      P (r) K (r)

- K ( r )sin² 6 dф²

Для краткости, коэффициенты P ( r ), J ( r , 6 ), K ( r ) будут записаны как P, J, K, кроме некоторых специальных случаев, которые будут оговоры.

3.2. Испускание частиц Дирака

В искривленном пространстве-времени уравнение Дирака определяется как:

ihy ^M D ^ — 0

где D - ковариантная производная. Она может быть определена как:

D =5 +1 a. гт ц     ц ^ ц ab,

Obab это спин соединения, который может быть описан как: ц ab a v^b _ar^v vb 1 vb     b     vb     a\

co — e с e +e 1 e =—(e о e — e о e ).

ц     v ц        v цо      ^x ц ц v        ц v ■

О _b - соответствует коммутатору гамма-матриц пространства-времени Минковского.

Oa = | [Ya , Yb 1

Чтобы выделить переменные, которые связанные с пространством-временем Минковского и искривленным пространством, были использованы два типа индексов. Латинский индекс указывает на локальные рамки (минковские), а греческий индекс указывает на переменную в искривленном пространстве-времени. Связь между минковскими гамма-матрицами с гамма-матрицами искривленного пространства-времени: у ^ц = е ^ц у^а . Существует несколько выражений гамма-матрицы Минковскиана, которые удовлетворяют условию:

{ y ^a , / ^b } = ^ n ab I . Запишем эти уравнение можно записать в виде:

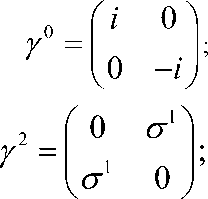
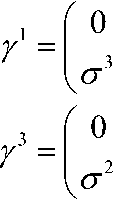
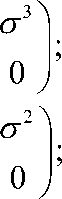
где О^к - матрицы Паули. В данном исследовании ненулевые компоненты тетрады были выбраны те, которые удовлетворяют условию: g ^_v = П^e a e b , следующим образом:

е ц = diag

^ 1 KP 1     1,                ,            ,^VP v J Jj kKsin#J

Используя тетраду, гамма-матрицы в эллиптическом пространстве-времени могут быть получены как:

yt =

1 Г i

Pp (О

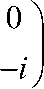
yr

KP Г о J (о3

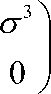
y ”

JCT

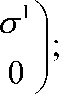
y' =

1KS sin”

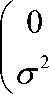
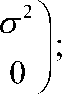
Спинорная волновая функция ψ имеет два спиновых состояния: спин вверх и спин вниз, поэтому выражение волновой функции для обоих состояний можно быть выражена как:

Is [ t, r ,6,ф\ n

i-s [ t, r м n где ^^ соответствует спин-вверх, и ^^ соответствует спин-вниз. S - это их действия. Однако в данной работе рассматривался случай спин-вверх, потому что случай спин-вниз просто аналогичен. Действие в приведенном выше определении может быть расширено в порядке постоянной Планка. Вывод из этой гипотезы может быть записан как:

S [ t, r, ”, ^\ = S0 [ t, r, ”,^\ + ^ anhnSn [ t, r, ”, Ф\        (16)

n

Для n = 1, 2, 3, ..., a — это константа, служащая для того, чтобы все члены разложения имели размерность действия. Из-за очень малого значения постоянной Планка, члены для n > 1 могут быть пренебречь [10, 5].

Подставляя уравнение действия в волновую функцию в уравнении

(15) и Дирака в уравнении (11), выраженные уравнения могут быть записать в виде:

iA

P

д, S + B. — 5, S = 0 tJr

B 5, s+ j 0

iB

Кк sin”

d ^ S = 0

iB       KP

-,=д.S + A, ---d_r S = 0

PtJr

A∂ S+

Jθ

iA

K sinθ

∂ϕS=0

Согласно методу Гамильтона-Якоби, действие может быть выражено следующими компонентами:

S = -Et+R(r) + Θ(θ) + Φ(ϕ)         (21)

где E – энергия, R – радиальная компонента действия, Θ и Φ – компоненты которые соответствуют азимутальному углу и полярному углу соответственно. Если A и B не равны нулю и используя уравнения (18) и (20), то мы приходим к одному уравнению. И оно может быть записано как

∂θΘ=

∂Φ JK sin θ

Решение вышеприведенного уравнения может быть получено путем интегрирования. Интегрируя получаем:

π

Θ = -∫

i∂ϕΦ

J K sinθ

dθ=

-2i

JK

∂ϕΦ

Ясно, что Θ не зависит ни от A, ни от B. Более того, уравнения (17)

и (19) имеют два возможных решения. Решение может быть записано как:

Для A = iB

∂rR=

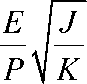
Для A =-iB

∂rR

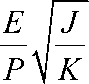
Соответственно, корреляция равна:

∂ r R± = ±

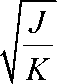
Знак плюс в приведенном выше уравнении соответствует решению для выходящей частицы и наоборот, минус для входящей. Вспоминая метрический коэффициент в уравнениях (7)-(9), решение для R может быть получено в результате интегрирования. Запишем это уравнение, как:

R±=∫

Er2+ a2 cosθ dr

P(r)     r2+ a2

Для статической черной дыры, ее частицы испускаются на горизонте событий. Поэтому метрический коэффициент P с помощью разложения в ряд Тейлора может быть расширен. Уравнение для P может быть записано как:

P(r) = P(r) + P'(r)(r - r) + O(r - r)2          (28)

Знак "плюс" определяет производную относительно радиальной координаты r. Таким образом, интегрирование вышеприведенных данных может быть решено следующим образом:

^r k + ⁵

R±=±J rk S

E

^P '( ^r k ^{)( r - r} k )

r2 + a2cos0 , dr r + a 2

rk +5

i ( r + ia cos 0 ) csc² (—)  ( ir + a cos 0 ) s e c² (—)

R ±=±

a + ir

a + ir

x

P *( r_k )( a ² + r k ²)

a ² + 2 r ² + a ²cos 0 /( a - ir ) tg 0

2  ,  „2

a + ir

^rk - ⁵

- 2( a ² + r_k ²) EllipticPi

2/ 0x • -1

-ctg (-),sin

ir ) tg ^{2 ( 0} a + ir

4 0Л , ctg ⁽-)

+

V

7         7

( a ² + 2 r ² + a ² cos 2 0 ) EllipticPi

,           i 0

( a + ir ) ctg —

-------------- ,sin a - ir_k

, 0

^{( a -} ir k ) tg ⁽-)

a + ir

—, ctg ⁴( | )

+

V

rk+5

a ( a - ir_k ) EllipticF

-1

sin

- ir ) tg ^{2 0} a + ir

t 4 0\ , ctg ⁽-)

sin² 0

rk-5

где EllipticPi соответствуют третьему эллиптическому интегралу третьего рода (неполному) и EllipticF - эллиптический интеграл первого рода (неполный). Применяя граничное условие для положения вокруг горизонта событий, можно легко обнаружить, что решение R содержит переменную, которая зависит от θ, a и r .

Таким образом, сравнивая приведенное выше радиальное решение действия для сферической симметричной черной дыры, получим

IE

R. = ±------ £ ( a , r , 0 )

±    P x rh )^ h где ^(a, r , 0) - функция, которая суммирует все переменные, которые зависят от а, r и θ. Если черная дыра не слишком эллипсовидная или она

2  ,    2       2

удовлетворяет условию a ~ r

r +a cos 0

то тогда                 может быть выражено, как

V r + a a2 (cos2 0 —1)

+   2^

+ O ( a ⁴) ,

и интеграл в уравнении (29) может быть решен как:

r h +⁵

R±=±J rh -5

_+ inE

E

^P '( r ,⁾⁽ r ^— r ,)

(        2  •  2z)

a sin 02r2

V       ² rh   ,

a 2( cos 20 — 1)

2 r

dr —

Из приведенного выше выражения ясно, что решение R в эллиптической черной дыре зависит от его азимутального угла. Для сферически симметричной черной дыры, a = 0, решение приведенное выше решение сведется к

inE

R+ — ±------. Эта корреляция находится в хорошо согласуется с предыдущими расчетами, например [12]. Другими словами, для сферически симметричного случая переменная ^ является постоянной (i,е,П).

В общем случае, решение для 0 и Ф как для выходящей частицы, так и для входящей частицы постоянны. Таким образом, выражение действия может быть записано как

/7?                -2/

⁵ + ^{—— Et +} P^^ ^ ⁽ a , r h ,^) ⁺ J^ ⁹ ^ ^Ф+Ф тЕ              -2/

5 — — Et-- 5 ( a,r , 0 ) + —^= д Ф + Ф

• —        p'(г, П , h, 7 j4k ф

Вспоминая волновую функцию спин-вверх в виде уравнение (15) и если почти все входящие частицы поглощаются или P_in — 1 , то вероятность выходящих частиц приводит к уравнению:

^P out = ^еХР

— 4 E hP '( r , )

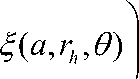
(34 )

Согласно методу Дамура-Руффини спектр излучения Хокинга для фермионного излучения:

Р ,г out

b out

где Г - поглощательная способность черной дыры. Поскольку вероятность входящих частиц Р_п — 1 , то ясно, что ее поглощающая способность равна единице, Г = 1. Поэтому, используя вероятность вылетающих частиц в уравнение (35) и с помощью определения коэффициента Больцмана, температура Хокинга для эллиптической черной дыры составляет:

hP'(rh) 4£( rh, a ,6)

Из приведенного уравнения (36) ясно, что температура зависит не только от ее горизонта, но и от полуоси a и азимутального угла θ. Этот результат весьма интересный. Поскольку температура зависит от азимутального угла, то каждая точка на поверхности черной дыры может иметь разную температура. Другими словами, эллиптическая черная дыра не удовлетворяет равновесным тепловым условиям. Это можно понять на основе зависимости между температурой черной дыры и ее по- k верхностной гравитацией, T —--- . По-

2п

черная дыра удовлетворяет условию сфе-

рической симметрии, ξ = π, ее температура

1   и P'( rh)

будет приводить к T —------- 4 п

.

4. Выводы. Благодаря излучению частиц Дирака, используя метод комплексного сопоставления, может быть выведена температура для эллиптической черной дыры. Из полученных результатов видно,

скольку каждая точка на поверхности имеет разное расстояние до ее центра, поверхностная гравитация эллиптической черной дыры также зависит от θ. Кроме того, если

что температура зависит не только от горизонта, но также от полуоси a и азимутального угла 6 . Следствием этого результата является то, что в эллиптической черной дыре ее поверхность имеет неоднородную температуру, следовательно она

не удовлетворяет условию теплового равновесия.