Математическая модель электромеханического исполнительного устройства для регулирования частоты вращения парового турбогенератора на базе линейного актуатора

Задача синхронизации синхронного генератора решается при подключении генератора в параллельную работу с системой электроснабжения [1] с помощью автоматических синхронизаторов [2]. При работе генератора могут действовать внешние возмущения, которые влияют на частоту вращения ротора. Это может привести к рассинхронизации параллельно работающих генераторов. Возникает задача синхронизации генератора во время работы. Для решения этой задачи необходимо использовать систему автоматического регулирования частоты вращения (САРЧВ) турбогенератора с возможностью допустимого варьирования задания частоты вращения на короткое время для введения генератора в режим синхронизации во время работы.

Существующие САРЧВ турбогенераторов используют непрямые центробежные регуляторы. Параметры маятника центробежного регулятора настроены на заданное значение частоты вращения турбогенератора, соответствующее стандартному значению частоты переменного напряжения 50 Гц. Внешние возмущения вызывают разность между углами вращения роторов генераторов. Тогда для синхронизированной работы возникает необходимость изменения скорости вращения ротора в пределах допустимых отклонений ±0,4 Гц. Этого достаточно, чтобы синхронизировать работу генераторов в течение 20 с. Но центробежные регуляторы не имеют возможности изменять значение задания частоты вращения, их параметры рассчитаны только на одно фиксированное значение.

Также применяются электрогидравлические регуляторы, которые имеют возможность изменять задание по частоте вращения. В электрогидравли-ческих и центробежных регуляторах исполнительным механизмом является гидравлический привод, для которого характерны недостатки гидравлических систем, и прежде всего это низкая точность при отработке сигналов управления, а также высокие затраты при эксплуатации [3].

Все эти вышеприведённые регуляторы используют золотниковые гидравлические двигатели для обеспечения «непрямого регулирования». Гидродвигатель обеспечивает САРЧВ паровой турбины инвариантностью к возмущениям со стороны давления пара на клапан в устройстве подачи пара в турбину. Тем не менее золотниковое устройство обладает проблемой «сухого трения», вызванного наличием перекрытий у золотника [4]. Это приводит к тому, что САРЧВ обладает некоторой нечувствительностью, для снижения которой создаются дополнительные устройства, что механически усложняет, а следовательно, снижает надёжность САРЧВ.

Наиболее перспективным является применение электромеханических регуляторов [5], которые построены на основе регулируемого электропривода с преобразованием вращения электродви- гателя в линейное перемещение рабочего органа. Такими электроприводами являются линейные актуаторы. Электрический привод дает высокую надежность и точность отработки сигналов управления и невысокие трудозатраты при эксплуатации.

Целью данной работы является объединение математического описания процессов, протекающих в паровом турбогенераторе, а также электромеханических процессов в линейном актуаторе, который непосредственно перемещает шток клапана в устройстве подачи пара, без участия гидродвигателя. В результате объединения этих моделей образуется модель объекта управления, к которой можно применить методологию теории автоматического управления (ТАУ) для создания САРЧВ агрегата «паровая турбина – генератор».

Регуляторы электромеханической САРЧВ будут реализовываться не механическими или гидромеханическими, а электронными устройствами либо алгоритмами программируемых логических устройств, с помощью которых можно реализовать любой закон управления. Это не только повысит динамические и статические показатели качества САРЧВ, но и повысит ее надежность. Устранение проблемы «сухого трения» позволит использовать линейную часть ТАУ, методы которой наиболее развиты, чем нелинейной части ТАУ.

Принцип работы паровой турбины с линейным актуатором

Примем, что используется паротурбина без промежуточного перегрева пара. На рис. 1а представлена система электромеханического регулирования положением штока клапана паротурбины. Исполнительным механизмом в системе электромеханической САРЧВ является линейный актуатор А, который перемещает свой шток на величину y . Шток актуатора через кривошипно-коромысловый механизм перемещает на величину x шток клапана К, с помощью которого регулируется подача пара в турбину Т. Таким образом, регулируется частота вращения ротора ω и, следовательно, мощность турбины P _т. Кривошипно-коромысловый механизм необходим для сочетания длины хода актуатора и клапана подачи пара: крайние положения штока актуатора должны соответствовать крайним положениям штока клапана.

Турбина вращает синхронный генератор Г, вырабатывающий электроэнергию для электрической сети с потребляемой мощностью P _э. Частота вращения ротора измеряется датчиком Д, на выходе которого формируется электронный сигнал, пропорциональный скорости ω, и сравнивается с задающим электронным сигналом ω^*. Сигнал ошибки, полученный в результате сравнения, возникает на входе регулятора частоты вращения Р. На выходе регулятора Р формируется электронный сигнал управления для электродвигателя линейного актуатора, который определяет значение скоро-

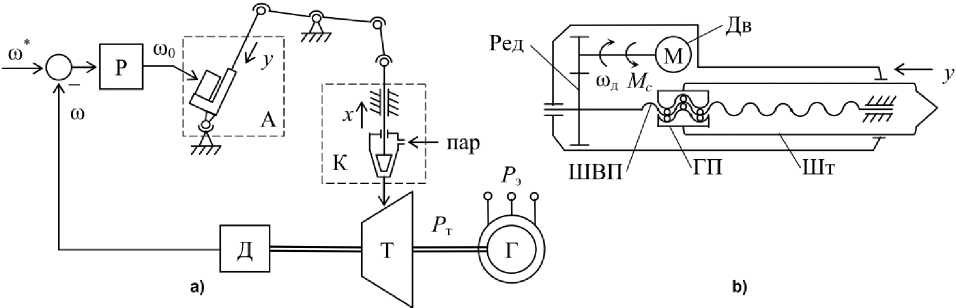
Рис. 1. Паровой турбогенератор с электромеханическим регулированием частоты вращения (а) на базе линейного актуатора (b)

Fig 1. Steam turbine generator with electromechanical speed control (a) based on a linear actuator (b)

сти идеального холостого хода электродвигателя актуатора ω0.

В зависимости от типа электродвигателя сигнал управления может регулировать любой параметр электродвигателя. Например, для двигателя постоянного тока это может быть напряжение якоря, а для асинхронного двигателя – частота напряжения статора.

Линейный актуатор (рис. 1b) представляет собой электрический двигатель Дв, вращающий через редуктор Ред винтовую передачу ШВП, которая преобразует вращательное движение электродвигателя в поступательное движение штока Шт актуатора. При этом необходимо учитывать, что имеются два типа винтовых передач: трапециевидная винтовая и шарико-винтовая.

Передача с трапециевидной резьбой характеризуется движением с высоким трением скольжения и, соответственно, с низким КПД. Но такая передача обладает статически самотормозящимся свойством, т. е. устранена возможность обратного преобразования поступательного движения штока во вращающееся движение двигателя актуатора под действием сил нагрузки на шток актуатора даже при выключенном двигателе. Это делает САРЧВ инвариантной к возмущениям со стороны давления пара на клапан в устройстве подачи пара в турбину. При таком техническом решении, как и в случае с золотниковым гидродвигателем, в САРЧВ возникнет проблема «сухого трения», т. е. необходимо приложить усилия электродвигателя для преодоления сил трения скольжения между поверхностями резьбы для начала движения штока.

Шарико-винтовая передача лишена этого недостатка. У неё высокий КПД и отсутствует статически самотормозящее свойство, но приходится учитывать действие нагрузки давления пара на клапан, который через кривошипно-коромысловый механизм будет передаваться на шток актуатора.

Математическая модель паровой турбины

Математическому описанию процессов в турбогенераторах посвящено достаточно много литературы, где рассматривается автоматическое регулирование турбинных установок. На основе обобщения материала можно выделить наиболее удобную модель парового турбогенератора, структурная схема которого представлена на рис. 2.

Здесь рассматриваются процессы в относительных отклонениях переменных. Примем за базисные номинальные значения положения клапана х_ном, скорости вращения to_ном, мощности электрической нагрузки Р_ном и момента на валу агрегата ^Мном ^.

Относительное отклонение скорости вращения вала агрегата:

to — to Ato

6to =       - =     .

toHOM toHOM

Относительное отклонение положения клапана турбины:

X — X Ax

6x =------ =----.

хном    XHOM

Относительное отклонение момента турбины, вызванное изменением электромагнитного момента генератора М г при изменении мощности потребления Р г :

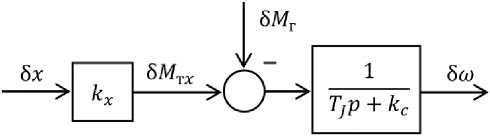
Рис. 2. Структурная схема парового турбогенератора Fig. 2. Structural diagram of a steam turbine generator

6Мг =

ДМг

М НоМ "

ны целесообразно применять регулируемый линейный актуатор, где управляющей величиной

Постоянная времени ротора турбины:

т _ т ^Шном

1J"JMHOM-

Коэффициент пропорциональности, характе-

ризующий изменение момента турбины М_т, вызванное изменением мощности турбины Р_т посред

ством отклонения положения клапана х:

кх

( ^дМт ) ^хном дх М ном

Коэффициент саморегулирования турбогене-

является скорость идеального холостого хода двигателя ш0. Для электроприводов постоянного тока плавное регулирование обеспечивают преобразователи напряжения на якоре, а для электроприводов переменного тока – преобразователи частоты статора.

На рис. 3 представлена структурная схема линейного актуатора, которая представляет собой структурную схему регулируемого электродвигателя и интегрирующее звено, связывающее ско-

ратора, учитывающий изменение относительных отклонений момента турбины и момента генерато-

ра в результате изменения скорости вращения ротора турбогенератора:

кс-КдММдМ)

^ ном

М НОМ "

Рассматриваемая модель, представленная в [6, 7], удобна тем, что помимо возмущающего воздействия 6Мг присутствует важная, с точки зрения

регулирования, внутренняя переменная – относительное отклонение момента турбины, которая обусловлена изменением давления пара в результате отклонения положения клапана Дх:

рость двигателя ш д и перемещение штока актуатора у, с коэффициентом, равным общему передаточному числу <_пр редукторной передачи и шариковинтовой передачи. Поскольку математическая модель является линейной, то переменные можно представить в отклонениях [9].

Механическая часть электропривода актуатора представлена в виде интегрирующего звена с коэффициентом, равным моменту инерции электропривода актуатора /пр, который складывается из момента инерции двигателя, передач актуатора и подвижного штока. Возмущающим воздействи-

6М„ = кх8х =

(дМ)

Дх

М НоМ

"

Математическая модель линейного актуатора

Линейный актуатор состоит из электродвигателя постоянного или переменного тока Дв (см. рис. 1b), который связан с шарико-винтовой передачей ШВП через цилиндрический, конический или червячный редуктор Ред. Гайка передачи ГП соединена с подвижным штоком Шт. В результате вращательное движение двигателя преобразуется в поступательное движение штока актуатора.

На сегодняшний день используются нерегулируемые линейные актуаторы, которые представляют собой готовую систему позиционирования штока [8]. Они обеспечивают перемещение штока со значительным усилием толкания и втягивания, достаточным для перемещения клапана мощной паровой турбины. Линейный актуатор в нерегулируемом варианте соответствует релейной системе управления. В этом случае применимы методы исследования систем со скользящим режимом.

Для обеспечения качественного позиционирования с высоким быстродействием клапана турби-

ем является отклонение статического момента на валу электродвигателя ДМ_С, обусловленное отклонением усилий давления пара на клапан турбины.

Электрическая часть электропривода актуатора представлена в виде апериодического звена первого порядка с электромагнитной постоянной времени Т э , которая в зависимости от типа привода определяется [9].

Для привода постоянного тока

_ ^яц э"Дяц ’ где Lяц, Rяц – индуктивность и активное сопротивление цепи якоря.

Для привода переменного тока

Т = э

,

Ш0ЭЛ"НОМ^К где ω0эл.ном – угловая скорость электромагнитного поля электродвигателя при номинальной частоте питания; sк – критическое скольжение.

Коэффициентом пропорциональности апериодического звена является жёсткость механической характеристики впр.

Для привода постоянного тока

сФ2

Q _ с ном впр = —R   ,

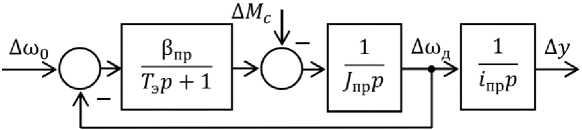
Рис. 3. Структурная схема регулируемого линейного актуатора Fig. 3. Structural diagram of an adjustable linear actuator

где с – конструктивный коэффициент двигателя постоянного тока; Ф ном – номинальный магнитный поток двигателя постоянного тока.

Для привода переменного тока

2Мк впР =      Г,

^Оном°к где Mк – критический момент электродвигателя.

Механическая и электрическая части электропривода охвачены контуром внутренней обратной связи двигателя.

Относительное отклонение управляющего воздействия электропривода актуатора:

Ato0

6to0 =------.

to0HOM

Относительное отклонение статического мо-

мента:

6Mc

АМС

Мд.ном

.

Объединение математических моделей парового турбогенератора и линейного актуатора

Для объединения двух моделей в один объект управления необходимо выполнить следующие преобразования:

1. В силу малости в сравнении с инерционностью турбогенератора целесообразно пренебречь электромагнитной постоянной времени линейного актуатора Т_э ~ 0. В результате в структурной схеме линейного актуатора апериодическое звено заменится пропорциональным звеном с коэффициентом пропорциональности в_пр. Это снизит порядок математической модели объекта управления в целом, что позволит упростить исследование объекта управления электромеханической САРЧВ. На рис. 4 представлена структурная схема актуатора при Т_э ~ 0.

На основании упрощённой структурной схемы составим математическое описание линейного

Относительное отклонение положения штока актуатора:

АУ

У ном^.

С учетом приведенных соотношений система дифференциальных уравнений работы актуатора (1) принимает следующий вид:

I

d6to

7п*р_dt^ — впр(5“0 - йШд) - 6Мс; . * d6y

■ ^1пр1Т ^{— 5Мд} .

Относительная величина момента инерции электропривода актуатора:

.*          ^to0HOM

Упр ^—^^прМ_№ом

Относительная величина жесткости механической характеристики электропривода актуатора:

• *          ^to0HOM

• ^впр = ^впр М д^ом^.

Относительная величина передаточного числа электропривода актуатора:

актуатора:

I

dAto

Л:'^Г = ₽np(Atoo - Atog) - АМС; dAy

^1пр ”dT = ^Atog

. *   .    уном

¹пр — ¹пр ~ ^ш0ном

.

2. Для согласования переменных модели тур-

богенератора и модели актуатора в последнем также необходимо привести к относительным отклонениям. В качестве базисных величин относитель-

ных отклонений примем номинальные значения на входах (номинальный момент двигателя М_д . _ном и номинальная скорость идеального холостого хода ш_0ном) и на выходе (положение штока у_ном, соот-

ветствующее номинальному значению положения клапана турбины хном) электропривода актуатора.

Относительное отклонение скорости враще-

• 3.    В масштабах относительных отклонений вполне допустимо приближенное равенство относительного отклонения положения штока актуатора и относительного отклонения положения клапана турбины, т. е. 6y = 6х.

• 4.    Необходимо учесть, что момент турбины М_тх оказывает на вал электропривода актуатора воздействие и, по сути, является статическим моментом на валу двигателя актуатора M _с. Тогда, с учетом передаточного числа электропривода актуатора 1_пр, можно представить статический момент в виде выражений:

M c

М тх ^ пр

ния вала электропривода актуатора:

или

6шд =

^Ашд ^to0HOM

5М,

6МТЖ

.

c

I * пр

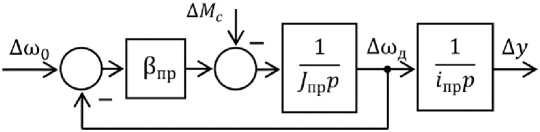
Рис. 4. Структурная схема регулируемого линейного актуатора в отклонениях Fig. 4. Structural diagram of an adjustable linear actuator in deviations

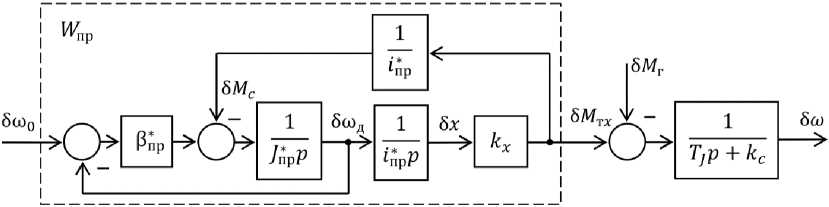
Рис. 5. Структурная схема объединённой модели актуатора и парового турбогенератора Fig. 5. Structural diagram of the combined model of the actuator and steam turbine generator

Вследствие двух последних замечаний можно объединить модели актуатора (см. рис. 4) и парового турбогенератора (см. рис. 2), структурная схема которого представлена на рис. 5.

В результате получим передаточную функ-

цию исполнительной приводной части парового турбогенератора, где представлен линейный ак-

туатор с шарико-винтовой передачей с учетом особенности влияния давления пара на клапан

турбины:

^пр(Р) =

6М„(р)

К пр

6ш₀ (р)    Т пр Т_змр ² + Т пр Р + 1

Коэффициент усиления приводной части:

К пр = в пр^р = в пр^^ном .

Мном

Механическая постоянная времени приводной

части:

₌ в пр ^ пр² ₌ в пр ^ пр^{2 Тпр} К (Ж^ Электромеханическая

•

^ ном

.

^ 0ном

постоянная времени

электродвигателя актуатора:

т =

эм

/пр _ /пр в р " в р .

Выводы

Разработана модель парового турбогенератора с линейным актуатором для прямого регулирования положения клапана в устройстве подачи пара в турбину. Модель представляет собой структурную схему из двух последовательно соединённых звеньев:

• 1)    инерционное звено второго порядка с передаточной функцией исполнительной части с сигналом управления для электродвигателя актуатора ш₀;

• 2)    апериодическое звено первого порядка, описывающее динамику вращения вала турбины с учетом саморегулирования и инерции вращающихся масс под воздействием момента турбины М_тх и момента генератора М_г как возмущающего воздействия.

Линейный вид математической модели позволит использовать методологию линейной ТАУ для синтеза регулятора Р (см. рис. 1) [10, 11], применять типовые настройки подчинённого регулирования, модального управления [12–15]. Также возможно применение перспективных методов нечёткого [16–20] и нейро-нечёткого управления [21].