Математическая модель электромеханической многокоординатной силокомпенсирующей системы

Сложные процессы создания и развертывания орбитальных космических станций приводят к большому количеству работ в открытом космосе на внешней поверхности станции и на удалении от нее, выполняемых непосредственно с участием космонавтов [1]. Опыт пилотируемой космонавтики показывает, что наиболее эффективным средством подготовки космонавтов являются тренажеры. Разработка и создание комплексных тренажеров, реализованных с использованием стендов обез-вешивания [2, 3], позволяющих имитировать движения в невесомости и в условиях пониженной гравитации, является важной и актуальной задачей.

Анализ различных подходов, применяемых для реализации пространственных перемещений космонавтов, показал, что для построения стендов обезвешивания рассматриваемых тренажеров необходимо скомпенсировать все силы, действующие на объект: силы трения, гравитационные силы, силы инерции дополнительно присоединенных к космонавту в скафандре масс. При выполнении этого условия космонавт будет двигаться под действием внешних усилий с требуемыми параметрами движения в невесомости. Построение таких стендов целесообразно осуществлять с использованием многокоординатных силокомпенсирующих систем (СКС) [4–6], обеспечивающих до шести степеней подвижности обезвешиваемого объекта. Причем реализацию составляющих движения целесообразно обеспечить суммой трех поступательных взаимно перпендикулярных движений, а также вращением и качанием объекта относительно его центра масс в кардановом подвесе.

Выполненные в [7] исследования позволили сделать вывод о целесообразности применения СКС, реализующих движение в виде трех поступательных взаимно перпендикулярных движений, реализуемых с использованием электроприводов, обеспечивающих требуемые пространственные перемещения космонавтов в рабочем пространстве тренажера [8].

Одной из задач, которую необходимо решать при создании многокоординатных СКС тренажера, является получение обобщенных математических моделей, позволяющих выполнять комплексные исследования, анализ статических, динамических показателей работы стендов обезвешивания, структурно-параметрического синтеза системы управления.

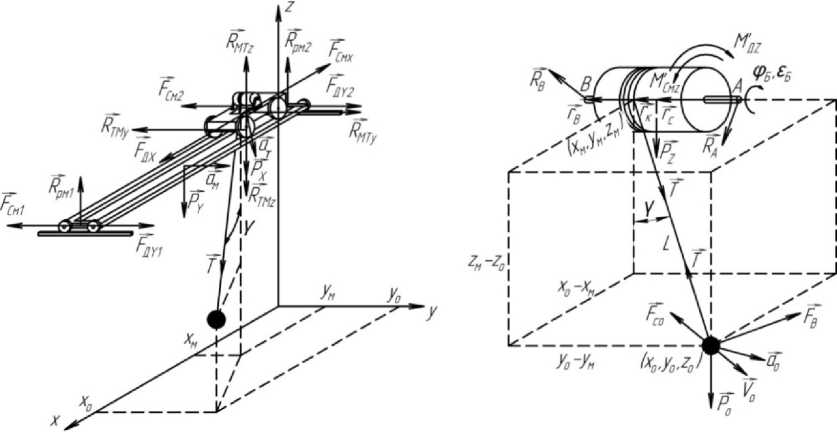
Анализ подходов к математическому описанию стендов обезвешивания показал необходимость рассмотрения составляющих движения космонавтов по трем координатам, с учетом силовых воздействий, прикладываемых к обезвешиваемому объекту. Математическое описание механической и электромеханической частей СКС с учетом специфики управления электродвигателями целесообразно выполнять с использованием модели двухфазной обобщенной электрической машины и метода обобщенного пространственного вектора [9]. Для получения математической модели механической части стенда обезвешивания, реализованного в прямоугольной системе координат, составлены его расчетные схемы, приведенные на рис. 1.

Для получения математического описания целесообразно применять следующие допущения: элементы конструкции моста и тележки под действием внешних сил не деформируются, мост и тележка имеют одну степень подвижности; направляющие, по которым обеспечивается перемещение моста и тележки, расположены в горизонтальной плоскости, положение тележки не влияет на значение коэффициента трения качения колес механизма моста; волновым характером распространения деформации каната можно пренебречь, канат невесом и в процессе работы всегда натянут, деформация каната подчиняется закону Гука; барабан жестко связан с тележкой, при намотке каната радиус барабана и точка схода каната остаются постоянными, что обеспечивается конструктивно; силы и моменты приложены к недеформи-руемым сосредоточенным неизменяемым массам; центр масс объекта обезвешивания всегда находится на прямой, являющейся продолжением каната; объект обезвешивания может свободно вращаться относительно точки крепления его к канату, поэтому моментом закручивания каната можно пренебречь.

Выделив в рассматриваемой механической системе четыре основных элемента, взаимодействующих друг с другом (мост, тележку, барабан и обезвешиваемый объект), с учетом действующих на них усилий и моментов, указанных на рис. 1, можно составить для каждого из них уравнение движения в векторной форме записи:

для моста

туам = FgY + T + Fcmy + Py + Px + Pz + R^ + Ям2;

для тележки

ma = F + T + F  + R + p + p ;

Х т    дX        СмХ    мт Х Z для барабана

J Б Ё Б = М g Z + М C м Z + [ r_K x T ] + [ Г в X R e ] + [ r X P z ];

для обезвешиваемого объекта mо ао = T + Fb + Po + Fco , где F дY , FдX – суммарная сила тяги двигателей моста и тележки; FСмY , F СмХ – силы сопротивления движению моста и тележки, обусловленные трением; PY , PX , PZ , Pо – суммарный вес моста, тележки, барабана и обезвешиваемого объекта с установленными на них механизмами; mY , mX , mо – суммарная масса моста, тележки и обезвеши-ваемого объекта с установленными на них механизмами; JБ – момент инерции барабана; ам , ат , ао – ускорение моста, тележки и обезвешиваемого объекта; ёБ - угловое ускорение барабана; Rэм1, Rэм2 , Rмт – силы реакции на мост со стороны эстакады и на тележку со стороны моста; F в – внешняя сила, прикладываемая к обезвешиваемо-му объекту; T = Txi + Tyj + Tzk - сила натяжения каната; TX , TY , TZ – проекции силы натяжения каната на оси X, Y, Z соответственно; i , j , k – ортогональный базис; МДZ, МCмZ - моменты двигателя системы вертикальных перемещений (СВП) и сил сопротивления, обусловленных трением, при-

а)                                                          б)

Рис. 1. Расчетные схемы для механической части стенда обезвешивания

веденные к валу барабана; r _к , r _в , r _с – радиусы-векторы точек приложения соответствующих сил T , R _в , P_Z , направленные из осей вращения барабана А ; R _A , R _в – силы реакции подшипников на вал барабана; х _о , у _о , z _о – координаты центра масс обезвешиваемого объекта; х _м, у _м, z _м – координаты точки схода каната.

Записав полученные уравнение моста в проекции на ось Y , тележки – на ось X , барабана – на его ось и обезвешиваемого объекта в проекциях – на оси X , Y , Z , с учетом уравнений взаимодействия

TX = T (Хм - Хо )/L ,

T Y = T ( У м — У о )/ L ,

Tz = T (zM - z о)/L, где L = \(xм - xо )2 +(Ум - Уо )2 +(zм - zо )2 - расстояние от точки схода каната до центра масс обезвешиваемого объекта, получим математическое описание механической части стендов обез-вешивания.

Выполненные исследования показали, что обычно угол отклонения каната от вертикали γ не превышает 2°, что позволяет линеаризовать тригонометрические функции в математическом описании СВП. Приведя переменные в полученных уравнениях к валам электроприводов соответствующих координат с учетом моментов инерции электродвигателей и механических передач, получим уравнения движения, описывающие взаимосвязанное движение исследуемых координат при приложении к обезвешиваемому объекту внешнего силового воздействия.

Анализ расчетных схем механизмов СКС показал, что модель каждой координаты СКС можно свести к двухмассовой электромеханической системе. Основное взаимодействие между координатами стенда обезвешивания происходит при изменении длины канатной передачи, обусловленной работой СВП. Это сказывается на изменении собственных резонансных частот СВП и системы горизонтальных перемещений (СГП).

Математическое описание электромеханических преобразователей выполнено с учетом того, что в СКС могут применяться двигатели постоянного тока (ДПТ), асинхронные двигатели (АД) и синхронные двигатели с постоянными магнитами (СДПМ) при работе до номинальной скорости. При использовании векторного управления АД с ориентацией по направлению вектора потокосцепления ротора ^2, векторного управления СДПМ при ориентации по вектору потокосцепления, создаваемого постоянными магнитами ротора, и использовании блоков компенсации перекрестных связей в АД и СДПМ [10], применения канала компенсации противоЭДС в ДПТ [5] математическая модель электромеханических преобразователей может быть представлена передаточными функциями с одинаковой структурой. С учетом математического описания регулируемого источника питания двигателя при наличии отрицательной обратной связи по току математическую модель многокоординатной СКС можно унифицировать, получив обобщенное математическое описание по вертикальной и горизонтальным координатам СКС. Единственным отличием математического описания по вертикальной и горизонтальным координатам СКС является отсутствие входного воздействия Мо для горизонтальных координат, так как это воздействие обусловлено действием силы тяжести, направленной вертикально. Структурная схема обобщенной математической модели СКС по одной из координат имеет вид, приведенный на рис. 2.

На рис. 2 приведены следующие обозначения: T _п - постоянная времени, учитывающая инерционные свойства преобразователя; k _п - коэффициент передачи преобразователя по напряжению; E _п – ЭДС преобразователя; W _рт( S ) – передаточная функция регулятора электромагнитного момента (тока) электродвигателя; k _дт – коэффициент передачи обратной связи по электромагнитному моменту (току) электродвигателя; J _д , J o = m o p ² -моменты инерции ротора двигателя и обезвеши-ваемого объекта; p - радиус приведения; с , b -коэффициенты, учитывающие жесткость и диссипативные силы упругой механической передачи; О д , О _о - скорости двигателя и объекта обезве-

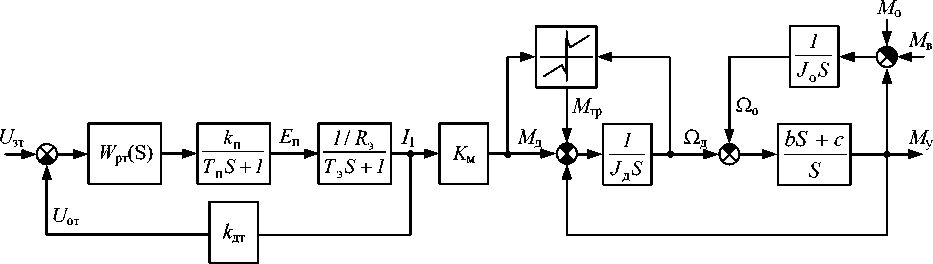
Рис. 2. Обобщенная математическая модель СКС

шивания; М _д , М _у – моменты двигателя и в упругой механической передаче; Т_э = L _{a 1} /( R 1 + к 2 R 2 ) , Т э = L _{o 1} / R 1 , Т э = L _яц / R _яц - электромагнитная постоянная времени статора АД, СДПМ и якорной цепи ДПТ; R _э = R 1 + к ₂ R 2 , R _э = R 1 , R _э = R _яц - эквивалентное сопротивление АД, СДПМ и ДПТ; R 1 , R 2 , L _{а 1} - активные сопротивления статора и ротора, приведенного к цепи статора, и индуктивность рассеяния обмотки статора АД; R 1 , L _{а 1} - активное сопротивление и индуктивность рассеяния обмотки статора СДПМ; R _яц , L _яц – активное сопротивление и индуктивность якорной цепи ДПТ; K м = ^1,5 k 2 Z р ^ 2ном , K м = ^1,5 Z р ^ f , K м = С Ф -коэффициент передачи для АД, СДПМ и ДПТ; Z р - число пар полюсов АД и СДПМ; v _2ном , V f — потокосцепление АД и СДПМ; k ₂ – коэффициент электромагнитной связи обмоток статора и ротора; С , Ф – конструктивная постоянная и поток возбуждения ДПТ; U _от – сигнал обратной связи по току (электромагнитному моменту) электродвигателя; U _зт – сигнал задания на ток (электромагнитный момент) электродвигателя; М _тр – эквивалентный момент трения.

Особенностью работы координат стенда обез-вешивания является необходимость более точно моделировать режимы стоянки и начала движения. Поэтому в характеристике трения целесообразно рассматривать три участка: при нулевой скорости, около нулевой скорости и при вращении электропривода. Следовательно, нелинейную характеристику момента трения целесообразно аппроксимировать тремя линейными участками [11]: участком момента трения покоя, участком с отрицательным наклоном и участком, на котором проявляется действие момента вязкого трения, математическое описание которого имеет вид:

М д ^{- М} у при | ^М д ^{- М} у | ^ ^М трп ^{и О} д = 0;

^М трп при | ^М д ^{- М} у| >  ^М трп и ^О д = 0;

M др Ч

^М трп sign ( ^О д ^{+ к} 1 ^О д ) ^{- к} 2 ^О д sign ( ^О д )

при⁰ <|° д| ^° п ;

М трд sign ( ^ д ) ^{+ к} вА при |И д | > О п.

Данная система уравнений позволяет учесть особенности влияния основных составляющих сил сухого и вязкого трения. При этом нелинейная характеристика трения аппроксимируется тремя линейными участками, как показано на рис. 3.

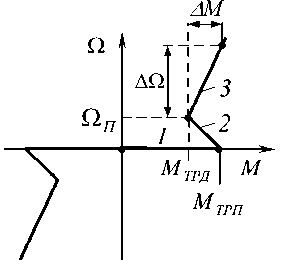
Рис. 3. Характеристика трения

Участок 1 аппроксимирует характеристику момента трения покоя M трп при О _д = 0 . Участок с отрицательным наклоном 2 – переход от трения покоя M _трп к трению движения M _трд , который заканчивается при скорости О д = О _п , а участок 3 – сумму моментов вязкого трения и трения движения M _трд . При этом значения коэффициентов определяются по формулам: к 1 = 10 3 ^ 10⁵, к 2 = ( M трп - M трд )/ О п , к вт = A M /АО .

Использование комплексного подхода к исследованию и синтезу СКС требует получения достоверного математического описания механической и электрической части электропривода. В модели механической части ЭМС необходимо определить такие параметры, как момент трения, коэффициенты жесткости и демпфирования упругой передачи. Нахождение их расчетными методами не всегда дает хорошие результаты. Поэтому необходимо использовать методы активной идентификации. При идентификации упруго-диссипативных свойств механической части СКС необходимо определять величины значений коэффициентов с и b для каждой из трех координат. Исследования показали, что коэффициенты с и b для СВП целесообразно определять по осциллограмме колебаний усилия в упругой механической передаче при приложении импульсного возмущающего воздействия к объекту, а для СГП по осциллограмме изменения угла отклонения каната при свободных колебаниях.

Переходный процесс изменения усилия в упругой механической передаче в СВП, полученный при подаче импульсного возмущающего воздействия, и переходный процесс изменения угла отклонения каната в СГП, полученный при свободных колебаниях, приведены на рис. 4. Осциллограммы получены на комплексе «Сармат» [2] при массе m o = 100 кг и высоте подвеса обезвешиваемого объекта 1,2 м.

Коэффициент жесткости механической передачи в рабочей точке можно определить исходя из того, что механическую часть электропривода можно представить в виде одномассовой динами-

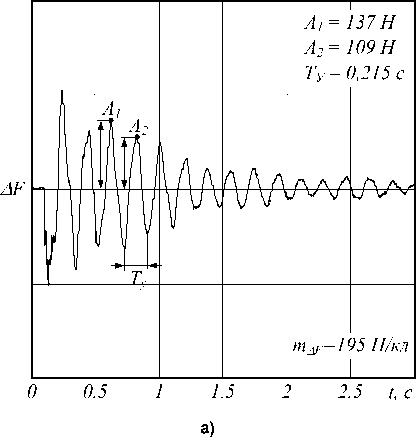
Рис. 4. Осциллограммы изменения усилия в СВП (а) и угла отклонения каната в СГП (б)

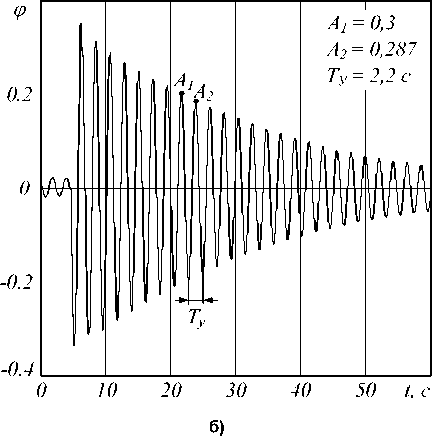
ческой модели с закрепленным в жесткой заделке упругим элементом. Тогда c = Jо (x2 + 4п2)/ту, где Ту - период колебаний; Х = ln(A1 )A2) - логарифмический декремент затухания; A1 , A2 – амплитуды двух соседних колебаний.

Для определения жесткости с для СГП можно воспользоваться расчетной формулой, согласно которой c = gm _о р ² L = gJ o / L , где g = 9,81м/с² -ускорение свободного падения.

Коэффициент демпфирования, учитывающий диссипативные свойства механической передачи, равен b = 2 TyX c = J x2 + 4п2    Ту "

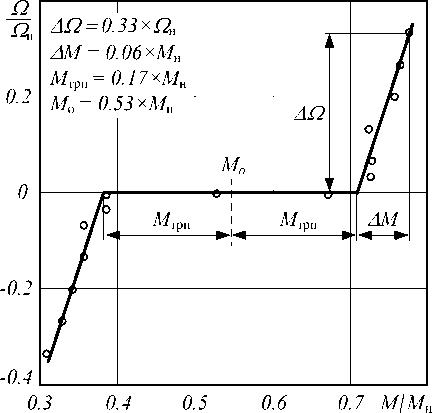
Для определения параметров характеристики трения целесообразно получить экспериментальную статическую характеристику. При снятии такой характеристики необходимо уделить особое внимание получению результатов при определении нагрузки электропривода при стоянке и скоростях, близких к нулю. Внешний вид статических характеристик, полученных для электроприводов СВП с СДПМ типа 1FК7044-7AF71-1FH5 ( М н = 3,5 Н·м, □_н = 314 рад/с), р = 1,875 • 10 ^{- 3} м и СГП с СДПМ типа 1FК7042-7AF71-1DH0 (М н = 2,6 Н·м, Ω н = 314 рад/с), р = Ы0 ³м комплекса «Сармат» [3] при массе объекта m _о = 100кг, показан на рис. 5.

Исследования показали, что при использовании СДПМ, моменты трения покоя и движения различаются незначительно ( M трп ~ M трд ), в то

а)

Рис. 5. Экспериментальные статические характеристики трения электроприводов СВП (а) и СГП (б)

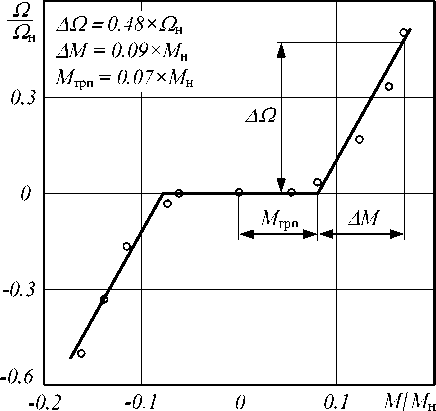
б)

Параметры обобщенной математической модели СВП и СГП комплекса «Сармат»

СВП СГП mо = 100 кг; р = 1,875 -10-3 м ; М о = 1,838Н - м; Jд = 1,28 -10-4 кг -м2; Jо = 3,52-10-4кг - м2; Мтрп = Мтрд = 0,595Н - м; квт = 2-10-3 Н - м - с/рад ; c = 0,301Н - м/рад; b = 7,47 •10"4Н-м - с/рад; R1 = 1,5Ом; Ьс1 = 0,02Гн; Тэ = 0,013с; Kм = 0,86Н-м/А mо = 100кг; р = 1-10 3 м ; L = 1,2 м ; Jд = 3,01-10-4кг -м2 ; Jо = 1-10"4кг - м2 ; Мтрп = Мтрд = 0,182Н-м; квт = 1,55-10-3Н - м - с/рад; c = 8,16-10-4Н - м/рад; b = 4 -10-6Н-м - с/рад; R1 = 5,15Ом ; Lо1 = 0,029Гн; Тэ = 5,6-10-3с; Kм = 1,4Н-м/А время как в СКС с ДПТ характеристика трения имеет явно выраженный участок с отрицательным наклоном (Mтрп > Mтрд).

С учетом изложенной методики идентификации упруго-диссипативных свойств механической части СКС и рекомендаций по определению параметров модели СДПМ [10], был выполнен расчет параметров обобщенной математической модели для СВП и СГП комплекса «Сармат» [3]. Результаты расчетов представлены в таблице.

С использованием полученной математической модели выполнены исследования упругосиловых взаимодействий многокоординатных СКС приведенные нами в [12].

Заключение

В результате выполненных исследований можно сформулировать следующие выводы:

• 1.    Для разработки единого подхода к построению систем управления различными координатами стендов обезвешивания и обобщения результатов исследования упруго-силовых взаимодействий в СГП и СВП их математическую модель рекомендуется представлять обобщенно, в виде эквивалентной двухмассовой ЭМС с упругой связью и с учетом трения на первой массе.

• 2.    Идентификацию упруго-диссипативных свойств механических передач стендов обезвеши-вания рекомендуется осуществлять для СВП по осциллограммам колебаний усилия в механической передаче, полученных при приложении к обезвешиваемому объекту импульсного возмущающего воздействия, а для СГП по осциллограмме изменения угла отклонения каната при свободных колебаниях.

• 3.    Нелинейную характеристику момента трения в СКС предлагается аппроксимировать тремя линейными участками: участком момента трения покоя, участком с отрицательным наклоном и участком, на котором проявляется действие момента

вязкого трения, параметры которого предложено определять по экспериментально полученным статическим характеристикам.