Математическая модель энергосберегающей технологии сушки зерна

Введение и цель работы. Снижение энергоёмкости процесса сушки зерна возможно за счёт совершенствования конструкций оборудования, технологического процесса и за счёт использования систем оптимального управления процессом 11]. Совершенствование управления процессом сушки требует наличия математической модели объекта управления, на базе которой может быть построена модель оптимального управления. Поскольку сушка - процесс тепло- и влагообмена между зерном и сушильным агентом, то необходимо рассмотреть данные закономерности и представить их в виде, удобном для построения систем управления.

Описание математической модели и ее обсуждение. Описание процесса тепло- и влагообмена в элементарном зерновом слое может быть представлено следующей системой уравнений [2, 3, 4]:

И/ = ______1У______     ;

Р [5,47-10”6 .(Г + 273)_

К = 7,1-10 ²._е⁰^;

dW

— + KW = KW„;

dr

^ ₊ 3600Г'-^ = -^^-- r?

dr         dR syBc8 dr 100-£^ece dr d6 = eyece dl' 36oor^sc« dT _ r* dW .

dr    yyy dr        y₃c₃ dR c. -100 dr

(I)

где Г- температура агента сушки, °C;

D — влагосодержание сушильного агента, г/кг;

W- текущая влажность зерна, %;

0- температура зерна, °C;

С - скорость агента сушки, м/с;

с_& с₃ - теплоемкость воздуха и зерна, кДж/кг °C;

£ - пороз ноет ь зернового слоя;

г' - скрытая теплота парообразования воды, кДж/кг;

у3-объемная масса зерна, кг/м3;

?в - удельный вес воздуха, кг/м3;

К коэффициент сушки, 1/ч;

W_p - равновесная влажность зерна, %;

R - радиус зерновки, м;

воздуха, подающегося в зерновой слой, рассчитывают его равновесную влажность Wp (1). Затем определяют коэффициент сушки К (2). Уравнение коэффициента сушки единичного зерна получено Г.С. Окунем [5]. Далее рассчитывают влажность зерна W (3). Потом температуру 7’, которую приобретает агент сушки после прохождения единичного слоя зерна (4). Затем рассчитывают температуру зерна 0 (5). После этого определяют влагосодержание D (6) и относительную влажность агента сушки на выходе из зернового слоя/' (7). Последовательное выполнение расчетов для каждого элементарного слоя позволит иметь полную картину динамики сушки зерна. Необ т — время, ч,

/’-относительная влажность воздуха, %.

Уравнения записаны в последова ходимо учитывать, что величина скорости Г сушильного агента может быть изменена на любом слое и на любом этапе расчета.

тельности их применения. По параметрам

Это позволит достаточно точно выполнять расчет сушки зерна в установках с радиальным распределением воздуха, при уравнении расходом вентилятора.

Современное прикладное программное обеспечение позволяет построить имитационную модель процесса сушки зерна в платном слое на базе модели элементарного слоя. Для построения имитационной модели элементарного слоя представим дифференциальные уравнения (3), (4), (5), (6) в виде передаточных функций.

Для уравнения (3) воспользуемся правилом замены [28] — = р и получим dz рКр) + Kw(p> = Kw^T), решения воспользуемся методом интегрального преобразования Лапласа. В этом случае преобразование частных производных осуществляется по следующему правилу [6]: если T = T(x,z) и преобразование Лапласа производится по переменной т(т < 0), то, обозначив

7ф7 Дү, т)] = Т(х, /?)J e"pr1\x7 z^dz, можно интегрированием по частям установить соотношение:

L

dT dz dT dz

= рПх7 р)-Т{х70»т

dT dx

откуда W_ww^ =

, ^гД^е W^p^ - не

где

7(л,0) - начальное значение темпера-

редаточная функция по каналу равновесная влажность - влажность зерна.

Уравнения (3), (4), (5) содержат частные производные. Для промежуточного их рТ (X, р)-Т(х,0) + 3600 ■ 1'^- = -dR туры.

Выполним преобразование Лапласа для (3) по т;

р@(х₇р) - —----pW7 р), юо-67 л;

или

рТ(х₇р) - Т(х₇0) + 3600 • V

dT

,— = -Axpe^x,p')-A1pW(.x,p), dR

где 4 - —

а2=—--

ЮО-б/с'

Решим дифференциальное уравнение относительно R*.

3600-И — = -А_үрӨ(х, р)- рТ(х₇ р) + 7Дх;0) - A^pW^xj?^ , dR

при этом р играет роль переменной. С учетом, что 7’(л,О) = 7_о, Д - температура воздуха на входе в зерновой слой.

Решение уравнения с использованием пакета MATLAB [7] при начальных условиях 7(0) = Уедало следующий результат:

T{p) = T„ Д - L '"') - A^p) - A₂pW(p), Р p

R

где z_A ----------.

3600-И

Уравнение (8) представляет собой зависимость изображения температуры теплоносителя 7(р) от изображений температуры агента сушки на входе в зерновой слой 7о(р), от изображения текущей температуры зерна Ө(р), от изображения текущей влажности зерна W(p). Такая запись дифференциального уравнения позволяет не выполнять сложные преобразования для записи результата в аналитическом виде, а представить его в виде набора передаточных функций. Решение будет представлено в виде трёх блоков: входное воздействие 7Др) и параллельное соединение двух вет-1

вен - интегрирующего звена — и интегри-Р рующего звена с звеном запаздывания

—е рг'; входное воздействие 0(р) и после-Р довательное соединение усилительного звена А] и дифференцирующего звена р; входное воздействие W(p) и последовательное соединение усилительного звена А2 и дифференцирующего звена р. Такое представление дифференциальных уравнений позволяет разрабатывать компьютерные имитационные модели и получать численные решения при любых начальных условиях.

Аналогичным способом осуществлялось преобразование дифференциальных уравнений (5) и (6). В результате проведенных преобразований получена полная система уравнений и передаточных функций, позволяющих выполнять расчет тепло- и влагообмена в элементарном слое зерна.

В укрупненном виде структурная схема расчета процесса тепло- и влагообмена в единичном зерновом слое приведена на рисунке 1.

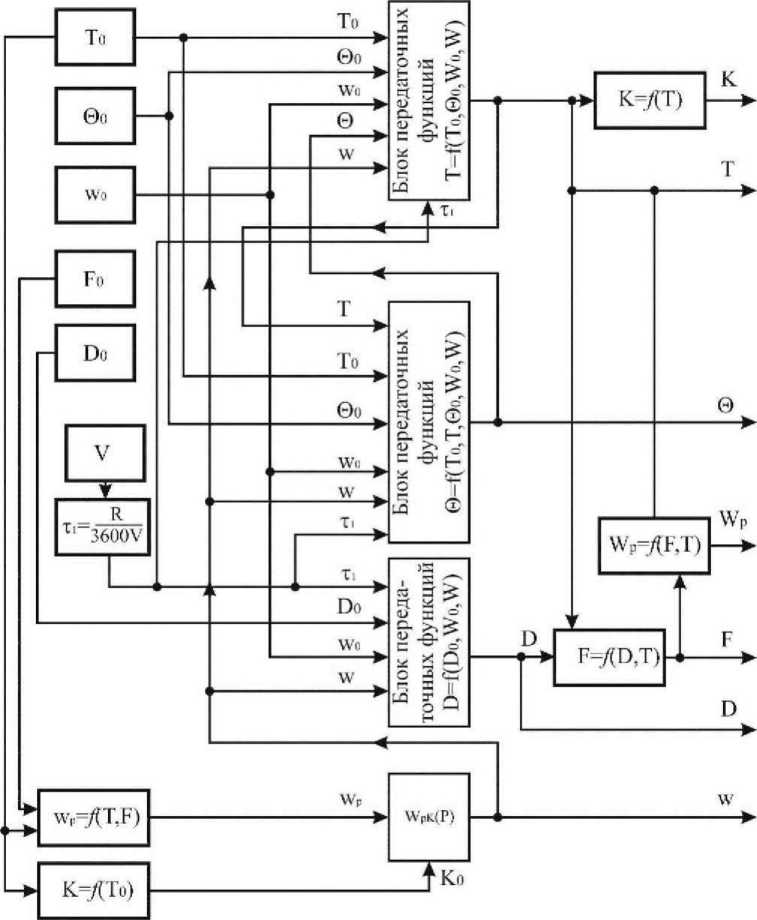
Рисунок 1 - Структурная схема сушки элементарного слоя

Энергосберегающая технология сушки предусматривает определение параметров зернового слоя в определённой зоне бункера активного вентилирования, определение энергозатрат на сушку слоя зерна при известных параметрах агента сушки

(относительная влажность, температура, скорость). В зависимости от того, какая стратегическая задача стоит (необходимо сушить с большей производительностью или с меньшими энергозатратами), определяют требуемую производительность вентилятора и схему перемещения зерна по зонам бункера. Для решения этих задач была разработана математическая модель. В основу модели положено уравнение теплового баланса для элементарного слоя [8]:

ДЛ-Г) = &+&+&, где L - массовый расход агента сушки, кг/с;

Л = ЬТрг,

5' - площадь поперечного сечения участка элементарного слоя (рисунок 2), м ;

V - скорость агента сушки, м/с;

р_в - плотность агента сушки, кг/м³;

6’ - порозность зернового слоя, о.е.;

/, - энтальпия агента сушки, поступающего в зерновой слой, кДж/кг;

1^ - энтальпия агента сушки на выходе из зернового слоя, кДж/кг;

Qn - количество теплоты, расходуемой на нагрев зерна, = у3с3 — кДж; СІТ

Он - количество теплоты, расходуемой на л ^dW п испарение влаги, Q_H = ^—-- кДж;

100 dr

Q_H - количество теплоты, теряемой в процессе сушки, кДж.

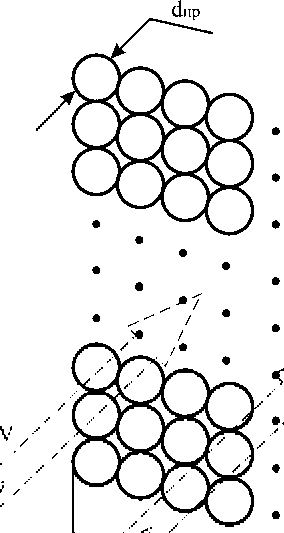
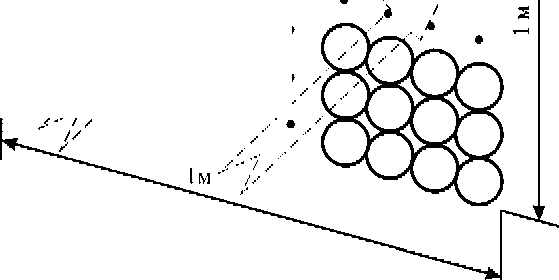
Рисунок 2 - Схематичное представление части элементарного слоя зерна площадью 1 м2, используемого для расчётов

Энтальпия агента сушки определится как [9]:

7 = (0,579-79 + сеГ)-4,19, где ск =(0,24+ 0,00047-/9)-4,19 - теплоёмкость воздуха.

Тогда Қ -Д =0,597-(Z)j -Р2) + 1,0056(Д -Д) + 0,00197(^7; -Д2Г2), где 7Р /2 - температура агента сушки соответственно на входе и выходе зернового слоя;

7}, 792 - влагосодержание агента сушки соответственно на входе и выходе зернового слоя.

При допущении, что производительность подачи агента сушки регулируют таким образом, что вся энергия агента сушки используется полностью, получено базовое уравнение сушки с учётом энергетического потенциала агента сушки:

5V р„е ■ [0,597 - (D_v - D₂) + l,0056(7; -7’₂) +0,00197(7), 7; -DJ\)\

= n-dnp

„ dO .   ,, yr dW

• 5 • ус — + и • d„„ • S • —--, dr 1    100 dt где dnp - приведённый диаметр зерновки, м;        Основным показателем процесса н- количество элементарных слоёв. сушки является влажность зернового слоя W. Запишем уравнение (9) относительно W;

— = -t-^"¹⁰⁰- - [0,597■ ф_х -IX ) +1,0056(7; - 7₂) + 0,00197(7),7( - D^)]-^^ — .

dr уУ-4ңр-п             ‘             ‘                        г' dr

После преобразований уравнение примет следующий вид:

dW Г г                                                          л ХӨ

---=—К, -[/.), (0,00197-/; + 0,597)+ 1,0056-7; -0,(0,597 + 0,00197-К)-1,0056-Г,]-^,—, dr п                                               '                  ’                  “ dr где

гЛУР"» п

ЮО-^ -------— Л. г' ■

Воспользовавшись принципом суперпозиции, получим передаточные функции, описывающие динамические свойства

влажности зерна по каналам «параметры агента сушки» и температуру зерна, которые используем в полной модели сушки зерна (рисунок 3).

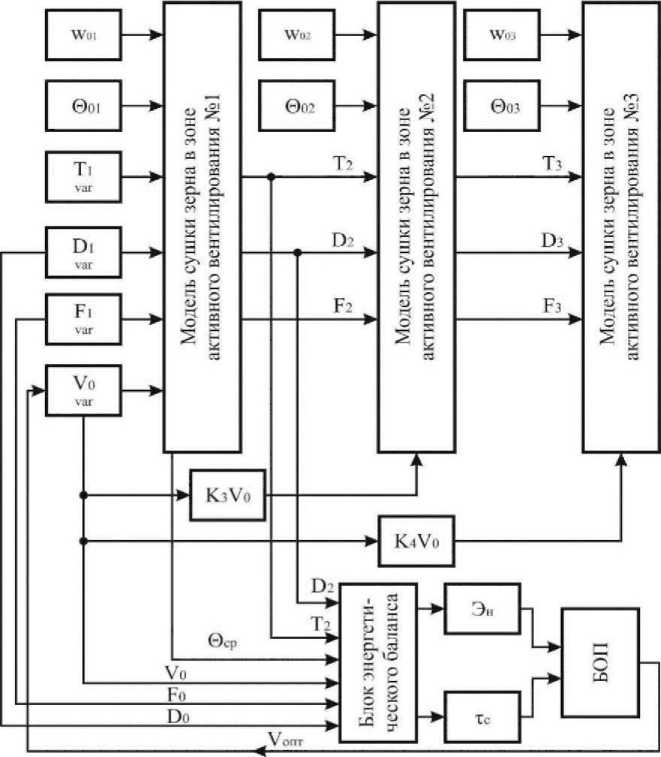
Рисунок 3 - Структурная схема полной модели процесса сушки зерна в секционных установках активного вентилирования

Полная модель процесса сушки зерна строится с использованием модели сушки в установках активного вентилирования плотного слоя с использованием модели сушки элементарного слоя (рисунок 1). Предполагается, что в бункере имеется возможность выпускать зерно из определённой зоны.

Схема работает следующим образом. Начальные параметры зернового слоя И^, Оо задают для каждой зоны бункера активного вентилирования. Задают начальные параметры атмосферного воздуха 7^ Во, Во и начальную скорость агента сушки Во. Параметры атмосферного воздух изменяют в процессе моделирования сушки в соответствии со среднесуточными графиками изменения температуры и влажности. Параметры агента сушки на выходе из зоны 7), В 2, В2 и 'В, Вз, Вз являются входными для следующей зоны. Скорость агента сушки в каждой зоне задаётся отдельно (уменьшается) в зависимости от размеров зоны и типа зерна. Для задания скорости агента сушки в каждой зоне входную скорость В_о умножают на соответствующий коэффициент Кз, К₄.

В процессе моделирования параметры воздуха на входе в зону То, Во, В„ и параметры агента сушки на выходе из зоны 7), В2 подают в блок энергетического баланса. Сюда же подают данные о средней величине температуры зерна по слою в зоне 0_ср. С использованием полученных данных в блоке энергетического баланса выполняется расчёт энергозатрат Эн на сушку зерна при данной скорости агента сушки в первой зоне бункера активного вентилирования и время т_с, в течение которого зерно достигнет требуемой влажности. В зависимости от того, по какому критерию ведут управление процессом сушки (минимум энергозатрат или максимум производительности) вносится корректировка в скорость агента сушки. Расчёт скорости агента сушки, обеспечивающей оптимальные энергозатраты, или скорость сушки осуществляет блок оптимизации (БОН).

Блок энергетического баланса с блоком оптимизации получают информацию и с других двух зон бункера активного вентилирования. В зависимости от стратегических задач, стоящих перед зернопунктом, может быть выбрана схема сушки зерна в зонах бункера. Это может быть перемещение зерна из зоны в зону по мере его подсушки или заполнение зон свежим зерном. С учётом данных задач блок оптимального управления будет определять требуемую подачу вентилятора.

Выводы

• 1.    Представленная система алгебраических и дифференциальных уравнений позволяет разработать модель сушки элементарного зернового слоя.

• 2.    Полученные с помощью преобразования Лапласа дифференциальные уравнения в операторном виде позволяют использовать для построения модели зернового слоя передаточные функции.

• 3.    Разработанная модель зернового слоя в виде передаточных функций позволяет моделировать процесс тепло - и вла-гообмена при изменяющихся параметрах агента сушки.

• 4.    Полная модель сушки зерна позволяет организовать управление процессом с учётом стратегических задач: максимальная производительность или минимальная энергоёмкость.