Математическая модель кинематического расчета плоских рычажных механизмов

На этапе проектирования плоских рычажных механизмов обязательно проводится кинематический расчет. Это операция очень трудоемка и содержит много вычислений. Поэтому является актуальным разработка математической модели

в форме процедур расчета кинематических характеристик любых плоских рычажных механизмов, имеющих в своем составе кроме начального звена хотя бы одну двух поводковую группу Ассура [1–3].

Разработка математической модели

Рассмотрим группу Ассура первого вида.

Положения звеньев данной группы Ассура определим с помощью рисунка 1, в котором представлена схема группы в соответствующей системе координат; обозначения звеньев и кинематических пар [4, 5]. Назовем конфигурацию групп сборкой № 1 когда координата точки В в локальной системе координат х 1 о 1 у 1 B y 1 > 0, в противном случае мы имеем сборку № 2. Известны координаты точек А, С в абсолютной системе координат, длины звеньев l ₂ и l ₃ и необходимо определить абсолютные координаты точки В, углы ф ₂ и ф ₃ . Расстояние АС определим по теореме Пифагора

АС — ^( С х - А х ) + ( С у - А у ) .

Угол α определим по формуле t f СУ - Ау) а = arctan —--- , f B - А ) v Bx - Ах J f B - C Л

Затем определяем углы наклона звеньев 1 2 , 1 з - Ф 2 и Ф 3

_m t f By - Ау )

Ф — arctan;

2         I Bx - Ах J f B - C )

Ф3 — arctan —---

Для определения аналогов скоростей воспользуемся методом замкнутых векторных контуров и напишем проекции векторного уравнения на координатные оси

A_x + 1 2 cos ф ₂ = C_x + 1 3 cos ф ₃ ;

A y + 1 ₂ sin ф ₂ — C_y + 1 ₃ sin ф ₃.

Продифференцируем полученные уравнения по обобщенной координате ф1. Учитывая, что нам известны значения аналогов скоростей точек А и С (Vax, Vay, Vcx, Vcy), а также значения углов φ2, φ3 получим линейную систему двух уравнений а для определения локальных координат Вх1 и Ву1, воспользуемся теоремой косинусов и теоремой Пифагора. Учитывая, что

B x i = 1 2 соs Z BAC, получаем

<у ₂ 1 ₂ sin to ₂ - m 3 1 ₃ sin m ₃ = Va x - Vc x ;

^Lcos^ - mkcosm = Vc^, - Va,,, yy

B x 1 =

1 22 + AC ² - 1 32 _

2 AC   ^;

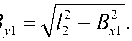
Здесь необходимо отметить, что если конфигурация группы Ассура соответствует сборке № 2, то B y 1 = – B y 1 . Теперь можно определить абсолютные координаты точки В, используя метод преобразования координат:

B x — A x + B x 1 cos a - B y 1 sin a ;

B y — A y + B x 1 sin a - B y 1 cos a .

где неизвестными являются аналоги скоростей m ₂, (У₃. Решение данной системы линейных уравнений проведем методом Крамера. В этом случае представляем уравнения в виде

^а11 ^Ю 2 ^{+ а}12 ® 3    b i.

;

a 2i ® 2 + a 22 ® 3 — b 2 ,

где коэффициентами a 11 , a 12 , a 21 , a 22 , b 1 , b 2 представлены следующие постоянные, известные нам по значениям, выражения:

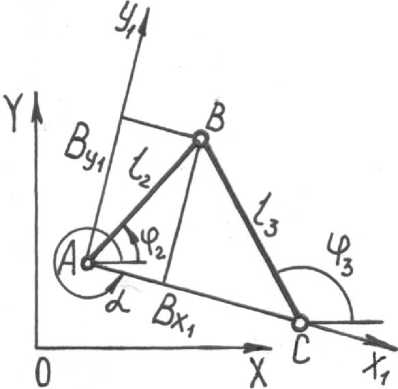
Рисунок 1. Расчетная схема группы Ассура первого вида

Figure 1. Settlement schemes of two flood groups of Assur first look

a n — - ^sin^. a_u — 1₃sin ф ;                                     ;

b i ^{— V}cx ^{- Va}x. ^a 21 ^{— 1} 2 ^cos Ф 2 ;

;

a ₂₂ — - 1 3 cos ф ₃ ; b ₂ — Vc y - Va y .

Тогда

b 1 a 12

b ₂ a ₂₂

2	a 11	a 12
	a 21	a 22

a ₁₁    b ₁

a ₂₁    b ₂

3	a 11	a 12
	a 21	a 22

Для получения аналогов ускорений дважды продифференцируем уравнения (1) по φ 1 :

Aa _x - о ₂²l₂cosф₂ - e ₂ 1 ₂sinф₂ — Ac _x

• - ю 2 l₃cosф₃ - e₃ 1 ₃sinф₃

;

Aa y - ® 2 1 ₂ sin ф ₂ - 8 2 1 ₂ cos ф ₂ — Ac y

• -m 2 1 3 sin ф ₃ - 8 3 1 3 cos ф ₃

Преобразуем полученные выражения к виду (3)

^11^2 + ai2^3 = b; a21^2 + a2263 = b2, где коэффициенты a11, a12, a21, a22 сохраняют свои старые значения, а b1 и b2 определяются по следующим зависимостям:

b i = Ac x — Aa x + a 21 ^ 2 + a 22 ^ 3 ;

b ₂ = Ac y — Aa y + a 11 ^ '2 + a 1. ^ 3 .

В этом случае, аналоги ускорений

S u и s ₃ будут равны:

E 2	b 1 b 2	a 12 a 22	;     ^3	a 11 a 21	b 1 b 2	.      (5)
	a 11	a 12		a 11	a 12
	a 21	a 22		a 21	a 22

Рассмотрим группу Ассура второго вида.

Схема данной группы Ассура, координатная система и обозначения кинематических пар и звеньев представлены на рисунке 2 [5]. Вычислим координаты точки А в локальной системе координат Х 1 СY 1

C x ⁺ A x 1 co ^ ^— A y 1 si ^ = A x ;

^Cy ⁺ A x 1 sin ^ ^— A y 1 cos ^ 3 = A y

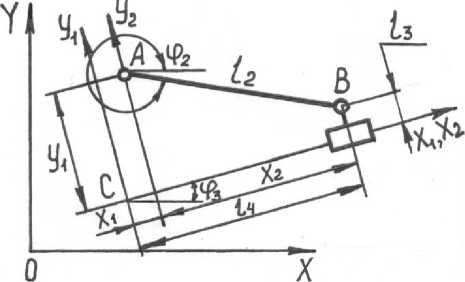
Рисунок 2. Расчетная схема группы Ассура второго вида

Figure 2. Settlement schemes of two flood groups of Assur second look

В выражении (6) нам известны абсолютные координаты точек А и С, а также угол наклона направляющей для поступательной пары группы - ф ₃. К числу неизвестных, подлежащих определению, относятся координаты точки А в локальной системе координат Х 1 СY 1 . Перенеся С х , и С у в правую часть, получим линейную систему двух уравнений, решение которой представим в виде:

b 1 — sin ф ₃

b2

cos ф ₃ — sin ф ₃

sinф3cos

A y 1 =

cos ф ₃ b 1

sinф3b cosф3 — sinф3 sinф3 cosф3

Здесь b 1 = A x – С x и b 2 = A y – C y . Так как определители знаменателей в (7) равны 1, то значения неизвестных равны значениям определителей, расположенных в числителях

A x 1 = b 1 cos ф ₃ — b ₂ sin ф ₃;

A y 1 = b 2 cos ф ₃ — b ₂ sin ф ₃.

Далее определяем х 2 – проекцию звена 2

на направляющую x2

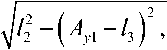
а затем и длину направляющей СВ l 4 = A x 1 + x 2 .

Абсолютные координаты точки В и угол наклона звена l2 определяем по следующим выражениям:

B_x = C x + 1 4 cos ф ₃ — 1 3 sin ф ₃;

B y = C y + 1 ₄ sin ф ₃ — 1 ₃ cos ф ₃ ;

m t f B y — A y 1 ^ = arctan —---- .

V B x A x 7

Для определения аналогов скоростей напишем проекции замкнутых векторных контуров на координатные оси X и Y

1 ₂ cos ф ₂ -1 ₄ cos ф ₂ = C x - A_x + 1 3 sin ф ₃ ;

2242 xx 33 (9)

1 ₂ sin ф ₃ -1 ₄ sin ф ₃ = C y — A y + 1 3 cos ф ₃ .

Произведя дифференцирование данной системы уравнений по φ 1 и простейшие преобразования, получим линейную систем уравнений, в которой неизвестными являются ω 1 и V 4

— ш ₂1 ₂ sin ф ₂ - V₄cos ф ₃ = V_cx

— V — < » ₃ ( l₃cos ^ + 1₄sin ^ )

;

ro ₂1 ₂ cos ф ₂ - V₄sin ф ₃ = V_cy

-V_ay - to ₃ ( 1 3 sin ф ₃ + 1 ₄ cos ф ₃ ) .

Решение данной системы уравнений получим в виде

0 2	b 1 b 2	a 12	; V 4 =-	a 11 a 21	b 1 b 2	,    (11)
	a 11	a 12		a 11	a 12
	a 21	a 22		a 21	a 22

где a11 = -12sinф2;        a12 = 13sinф3;

^b1 = Vc x ^- Va x + ^O 3 ( ¹ 4 a 22 + ¹ 3 a 12 ) ;

(12) a 21 = 1 ₂ cos ф ₂ ;          a ₂₂ = - 1 ₃ cos ф ₃ ;

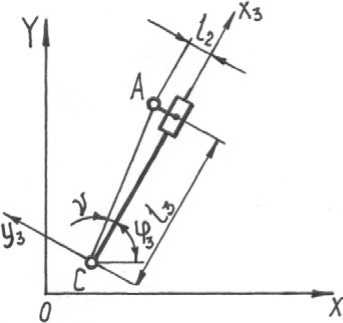
Рисунок 3. Расчетная схема группы Ассура третьего вида

Figure 3. Settlement schemes of two flood groups of Assur third look

b ₂ = Vc y - Va y - O ₃ ( 1 ₄ a ₂₂ - 1 ₃ a ₁₂ ) .

Дважды продифференцировав (9) и проведя небольшие преобразования, получим значения аналогов ускорений ε 2 и A 4

b1 a12 a11 b1 e 2 b2 a22 ; a4 == a21 b2 ,   (13) a11 a12 a11 a12 a21 a22 a21 a22 где a11, a12, a21, a22 определяются из (12), b1 и b2 вычислим следующим образом:

b₁ = Ac x - Aa x - 0 3 ( 1 ₄cosф₃ -l₃sinф₃ )

+0 2 1 ₂ cos ф ₂ - 2V₄o₃ sin ф ₃

Запишем проекции векторных уравнений замкнутых контуров на оси координат X, Y в следующем виде:

1 ₃ cos ф ₃ - 1 ₂ sin ф ₃ = A x - C x ;

1 ₃ sin ф ₃ - 1 ₂ cos ф ₃ = A y - C y .

Продифференцировав (17) по ф i, получим, после небольших преобразований, систему уравнений aiiV3 + ai2O3 = bi; a21V3 + a22O3 = b2, (18)

где a11 = cosф3;       b1 = Vax - Vcx;

a ₁₂ = - ( 1 ₃ sin ф ₃ + 1 ₂ cos ф ₃) ;

a ₂₁ = sin ф ₃ ;         b ₂ = Va y - Vc y ;

- ^ ( 1₄sin ^ + 1₃cos ^ )

;

b ₂ = Ac y - Aa y - 0 2 ( 1 ₄ sin ф ₃ - 1 ₃ cos ф ₃ ) ( )

a ₂₂ = 1 ₃ cos ф ₃ - 1 ₂ sin ф ₃ .

+0 2 1 ₂ sin ф ₂ - 2V₄ o ₃ cos ф ₃

-s ₃ ( 1 ₄ cos ф ₃ + 1 ₃ sin ф ₃ )

Следовательно, можно легко получить значения аналогов скоростей V 3 и ω 3 . После проведенных промежуточных преобразований, приходим к следующим выражениям для нахождения аналогов скоростей V 3 и ω 3 .

Рассмотрим группу Ассура третьего вида.

Положения звеньев данной группы можно определить, воспользовавшись данными рисунка 3 [3, 5]. Длину активной части кулисы l 3 определим из выражения

1 3 =V ( A x - C x ) 2 + ( A y - C y ) 2 - 1 22 , (15)

	b 1	a 12		a 11	b 1
V —-	b 2	a 22		a 21	b 2
V 3	a 11	a 12	; o 3 =	a 11	a 12	. (20)
	a 21	a 22		a 21	a 22

Продифференцировав дважды (17) по φ 1 и решив полученную систему уравнений, имеем:

где координаты точек А и С и длина второго звена l 2 известны. Угол наклона кулисы φ з определим из выражения

ф ₃ = arctan

( A y

-c 3

Cy

-

I A_x - C x

arctan

V ¹ 3 J

. (16)

A 3 = b1 b2 a12 ; ^*3 a11 a21 b1 b2 ,    (21) a11 a12 a11 a12 a21 a22 a21 a22 где a11, a12, a21, a22 определяются из (19), а b1 и b2 – по следующим выражениям:

b — Aa x — AC x + 2 V 3 ^ 3 a 21 + a 22 ^ 3 ;

₂     (22)

b — Aa — Ac., + 2 Voxa + a._? ^ . yy

Продифференцировав систему уравнений (23) по φ 1 , получим после простых преобразований:

Группа Ассура четвертого вида

Положения звеньев данной группы Ассура определим по рисунку 4, на котором приведены обозначения звеньев и кинематических пар [3, 5]. Запишем систему уравнений замкнутого контура в проекциях на координатные оси X, Y

A x + 1 1 cos ф ₂ — 1 ₂ sin ф ₂ — C x + 1 4 cos ф ₃

— 1 ₃ sin ф₃,

^;                (23)

A y + 1 1 sin ф ₂ + 1 ₂ cos ф ₂ — C y + 1 ₄ sin ф ₃

b1 a12 a11 b1 V — b2 a22 V — a21 b2 , (26) v 1— a11 a12 ;     V4 — a11 a12 a21 a22 a21 a22 где a11, a12, a21, a22 определяются из (25), a b1 и b2 – по выражениям:

b — Vc_x — Va x + ® 2 ( 1 1 a 21 + 1 2 $ h ) + +® з ( 1 4 a 22 + 1 3 a^ )

b ₂ — Vc y — Va y + rn ₂ ( 1 1 a_u + 1 ₂ a ₂₁ ) +

+® з ( 1 4 a ^ + 1 3 a 22 )

— 1 ₃ cos ф ₃ .

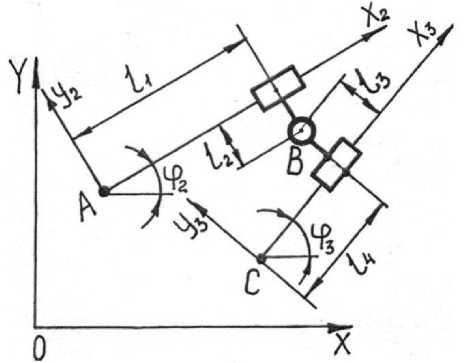
Рисунок 4. Расчетная схема группы Ассура четвертого вида

Дважды продифференцировав (23) по φ 1 , можно получить

A 1 —

b1

b2

a11

a21

; a 4 —

a11

a21

a11

a21

, (28)

где a 11 , a 12 , a 21 , a 22 определяются из (25), a b 1 и b 2 – по выражениям, которые после всех промежуточных преобразований имеют следующий вид:

^Ь 1 ^— Ac x ^{— Aa}x ⁺ 2 V 1 ^ 2 a 21 ⁺ + ^ 2 ( 1 1 $ц — 1 1 a 21 ) + 8 2 ( 1 1 a 21 + 1 2 $ц )

b 1 — b 1 + 2 V 4 ^ 3 a 22 +

Figure 4. Settlement schemes of two flood groups of Assur fourth look

Неизвестными в данных выражениях являются l ₁ и l ₄ , а остальные данные передаются в процедуру и являются известными. Полученная система уравнений является линейной относительно неизвестных. Запишем решение этой системы в виде:

+ ^ 3 ^{( 1} 4 a 12    1 3 a 22 ) + ⁸ 3 ^{( 1} 4 a 22 ^{+ 1} 3 ^a 12 )

b ₂ — Ac y — Aa y + 2 V 1 ^ ₂ a 11 +

+ ^ 2 ^{( 1} 1 a 21    ¹ 1 a n ^{) + 8} 2 ( ¹ 1 ^a 11 ^{+ 1} 2 ^a 21 )

b 2 — b 2 + 2V 4 ® 3 a 12 +

+ ^ 3 ( 1 4 a 22 — 1 3 a 12 ) + 8 3 ( 1 4 a 12 + 1 3 a 22 )

b ₁

b ₂

a ₁₂

a 22

a 11    a 12

a 21    a 22

a ₁₁    b ₁

a 21    b 2

4	a 11	a 12
	a 21	a 22

где коэффициенты a 11 , a 12 , a 21 , a 22 , b 1 , b 2 определяются по выражениям:

a_n — cos ф ₂ ;          a ₁₂ — — cos ф ₃ ;

b l ^{— C}x ^{— A}x ^{+ 1} 2 a 21 ^{+ 1} 3 a 22 ^;

a ₂₁ — sin ф ₂ ;          a ₂₂ — — sin ф ₃ ;

Ь 2 — C y — A y — 1 2 йц + 1 з $ 12 *

Группа Ассура пятого вида

Положения звеньев определим с помощью рисунка 5, где приведена схема группы, обозначения звеньев и кинематических пар и система координат [3–10]. Напишем проекции замкнутого векторного контура на координатные оси X, Y

A x — C x + Bx ₃ cos ^ ₃ + Ax ₂ cos ( ^ ₃ + а ) —

• — 1 ₂ sin ( ф ₃ + а )

^;               (30)

A y — C y + By ₃ sin ф ₃ + Ay ₂ sin ( ф ₃ + а ) —

• — 1 ₂ cos ( ф ₃ + а )

Выражения (30) легко приводятся к линейной системе двух уравнений, решение которых мы проведем по правилу Крамера

b 1    a 12

Bx 3 =

b2

a11

a21

;

	a 11	b 1
Ax 2 =-	a 21	b 2	, (31)
	a 11	a 12
	a 21	a 22

b₁ = Va x - Vc x

+^№ 3 ^{( B}x 3 a 21 ⁺ A X 2 a 22 ^{+ 1} 2 a 12 ) ;

b 2 = Va y ^- Vc y

+^№ 3 ⁽ B x з a n + A x 2 a ^ + l 2 a 22 ) .

где коэффициенты a 11 , a 12 , a 21 , a 22 , b 1 и b 2 определяются по следующим зависимостям:

Дважды продифференцировав выражения (30) по φ 1 получаем выражения для определения аналогов ускорений Ab x 3 и Aa x 2

a₁₁ = cos ф ₃ ;       a ₁₂ = cos( ^ ₃ + a ) ;

a 21 = sin ф ₃ ;       a 22 = sin( ^ ₃ + a ) ;

b1 a12 a11 b1 Ab x 3 = - b2 a22 ; Aax3 =- a21 b2 , (35) a11 a12 a11 a12 a21 a22 a21 a22 где a11, a12, a21, a22 определяются из (32), a b1 и b2 – по выражениям:

^b1 = ^Ax - ^Cx ^{+ 1} 2 a 22 ^;

b 2 = A y ^- C y + l 2 a i2 .

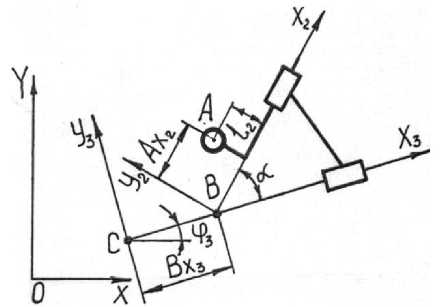
Рисунок 5. Расчетная схема группы Ассура пятого вида

Figure 5. Settlement schemes of two flood groups of Assur fifth look

b₁ = Aa x - Ac_x

+ 2 № ₃ ( Vb x 3 a ₂₁ + Va x ₂ a ₂₂ )

+№ 3 ⁽ B x 3 ^a _n + A x 2 a i2 ^- l 2 a 22 )

^£ 3 ^{( B}x 3 a 21 ⁺ A x 2 a 22 ^{+ 1} 2 a 12 ) ; b 2 = Aa y ^- Ac y

^{- 2 №} 3 ( ^Vbx 3 a ll ^{+ V} a x 2 a 12 ) +^№ 3 ^{( B}x 3 a 21 + A x 2 a 22 ^{- 1} 2 a i2 ) ^- ^ 3 ^{( B}x 3 a ll ⁺ A x 2 a 12 - ¹ 2 a 22 )

Продиффиринцировав выражения (30) по φ 1 , получим выражения для определения аналогов скоростей Vb x 3 и Va x 2

b 1    a 12

a ₁₁    b ₁

Vb

b ₂    a ₂₂

a 11    a 12

V a

a ₂₁

a 11

b ₂ a 12

, (33)

a 21

a 21

a 22

где a 11 , a 12 , a 21 , a 22 определяются из (30), a b 1 и b 2 – по выражениям: