Математическая модель комплексной безопасности компьютерных систем и сетей на основе экспертных суждений

Обеспечение безопасности является одной из основных проблем функционирования компью- терных систем и сетей. Исследованию в этой области посвящено большое число работ, в которых предлагаются различные подходы.

Так, например, в [1] изложен системный подход к построению комплексной защиты информационной системы (ИС) предприятия и описана методика построения такой системы с применением отечественных технических и криптографических средств защиты. В работе [2] рассмотрены принципы и методы аудита информационной безопасности (ИБ) на основе процессорного подхода, приведены некоторые методы оценивания ИБ.

Наиболее яркое выражение системный подход к решению задач ИБ нашел в работах В.В. Дома-рева. Им предложена трехмерная модель информационной безопасности, включающая в себя основные этапы, направления и методы обеспечения безопасности различных систем [3]. Подчеркнуто, что специфическими особенностями задачи создания систем защиты информации (СЗИ) являются:

• •    неполнота и неопределенность исходной информации о составе ИС и характерных угрозах;

• •    многокритериальность задачи, связанная с необходимостью учета большого числа частных показателей (требований) СЗИ;

• •    наличие как количественных, так и качественных показателей, которые необходимо учитывать при решении задач разработки и внедрения СЗИ;

• •    невозможность применения классических методов оптимизации.

Нарушение безопасного режима функционирования системы может наступить в результате целого ряда взаимосвязанных между собой причин. Любые неконтролируемые внешние или внутренние процессы потенциально могут привести к возникновению угроз. Реализация этих угроз в свою очередь вызывает деструктивные процессы и оказывает негативное влияние на безопасность. Нарушается нормальное функционирование системы, что находит отражение в значениях различных критериев и показателей, используемых для оценки безопасности.

В подобных случаях критерий выбора в ситуации принятия решения (СПР) представляет собой совокупность отдельных критериев, и соответствующая задача становится многокритериальной.

При решении многокритериальных задач часто используются различные методы свертки критериев в один обобщенный (интегральный) критерий.

Наиболеепростойметод построенияинтеграль-ного критерия заключается в выделении одного из критериев в качестве основного, а все остальные критерии добавляются к ограничениям, в которых задается область допустимых значений вектора независимых переменных. Таким образом, задача с векторным критерием сводится к задаче принятия решения со скалярным аргументом.

Основной недостаток такого подхода заключается в том, что фактически поиск ведется лишь по одному критерию. Значения остальных критериев, если они удовлетворяют ограничениям, по существу не влияют на результаты поиска.

Кроме того, безопасность – понятие комплексное и попытка оценить ее уровень по одному какому-то параметру (например, имеющему стан- дартное количественное выражение) обречена на неудачу. Поэтому данный способ получения свертки при решении задач, связанных с безопасностью неприемлем.

Другими методами построения комплексного критерия являются аддитивная и мультипликативная свертка.

Аддитивный критерий, являясь наиболее простым, в тоже время из-за возможности неограниченной компенсации значений одних критериев за счет других, нечувствителен к крайним значениям отдельных критериев.

Кроме того, комплексная безопасность не может рассматриваться как простая сумма составляющих ее частей.Эти части взаимосвязаны и взаимозависимы, каждая часть критично значима. Следовательно, модели, в основе которых лежит предположение о линейном поведении системы (аддитивная свертка предполагает именно такую модель), при оценке уровня комплексной безопасности обычно не могут адекватно отражать ситуацию. Поэтому аддитивная свертка для оценки уровня безопасности, в большинстве случаев, также не подходит.

Значение же мультипликативного критерия, в отличие от аддитивного, резко уменьшается при малых значениях отдельных критериев, что позволяет исключить нежелательные варианты при принятии решения.

Таким образом, для задач, связанных с обеспечением комплексной безопасности, наиболее целесообразным представляется применение мультипликативной свертки векторного критерия:

K = ∏ Kiμi i =1

где K_i – частные критерии, μ i – некоторым образом определенные веса, приписываемые каждому частному критерию K_i .

При построении свертки с целью унификации разнородных критериев используют переход от абсолютных значений критериев к относительным величинам.

Для этого фиксируется шкала возможных значений для критериев и возможные границы изменения для каждого из них. Например, если в качестве шкалы принят ь [0; 1], а гран ицы из- min max менения критерия K_i лежат между K _i и K _i то в качестве относительного значения критерия будет выступать величина:

K =

K i

_K min

_K max

_K min

Часто получение от лица,принимающего решение (ЛПР),надежной количественной информации для построения K ,бывает затруднительным.В таких случаях стремятся получить от ЛПР,в основном,только качественную информацию.Например,о том,какой из критериев наиболее или наименее значим,какой из критериев может быть ухудшен,а для каких ухудшение крайне нежелательно и т.д.

В качестве такой процедуры получения информации может быть использован алгоритм Беленсона-Ка-пура [4].

Многие аспекты,касающиеся безопасности сис-темы,могут вообще не подлежать количественному измерению.

Тогда при их оценивании прибегают к искусственным приемам.Например,каждому фактору сопоставляется количественная балльная шкала [5].

При этом необходимо предложить эксперту методи-ку,по которой ондолжен назначитьбаллы.Однако проблема заключается в том,что многие понятия,связан-ные с безопасностью являются сугубо качественными и,как отмечалось выше,предлагать измерять их количественно в большинстве случаев бесперспективно.

Другое дело,если сразу применять нечетко выраженные степени,например «Очень Низкая,Низкая, Средняя,Высокая,Очень Высокая».

Тогда от эксперта не требуется количественной точности,а требуется как раз субъективная оценка на естественном языке.Затем лингвистическое описание может быть сопоставлено с количественной (напри-мер,балльной)шкалой носителя с помощью методов теории нечеткого гранулирования [6].

Постановка и решение задачи

Необходимо создать методику комплексной оценки уровня безопасности компьютерной системы, основанной на качественных шкалах и отношениях предпочтения между факторами в структуре иерархии этих факторов.

Введем определение матрицы безопасности (МБ) системы B :

_⎜⎛K 1 F 1 V 1 S 1 T 1 _⎟⎞

⎜ ^K 2 ^F 2 ^V 2 ^S 2 ^T 2 ⎟

B=

⎜ K 4 F 4 V 4 S 4 T 4 ⎟

⎜⎟ ⎝ n n n n n⎠ где Ki – показатель уровня безопасности по i-му критерию; Fi - тенденция изменения i-го критерия (возрастает,убывает, нейтрален); Vi - скорость изме- нения i-го критерия (например: очень низкая, низкая, средняя, высокая, очень высокая); Si – степень приемлемости негативных последствий при реализации рисков,характеризуемых i-ым критерием; Ti – характерное для i-го критерия время,которое, в частнос-ти,позволяет правильно интерпретировать значения параметра Vi.

Первый и четвертый столбец МБ представляют собой вектор частных критериев безопасности и их весов и характеризуют текущее состояние комплексной безопасности,позволяя оценить сложившуюся на текущий момент времени ситуацию.Остальные столбцы матрицы отражают динамику развития процессов и позволяют строить прогноз развития на будущее.

В этом случае,мультипликативная свертка (интегральный критерий) комплексной безопасности представляет собой величину:

K = ∏ K iSi

i=1

Оценки S_i могут быть получены экспертным путем.Однако для эксперта в большинстве случаев затруднительно дать непосредственные численные оценки этим коэффициентам.Поэтому предпочтительнее могут оказаться различные ранговые методы, при реализации которых требуется лишь упорядочить критерии.

Может быть использован, например, метод нестрогого ранжирования.В соответствии с этим методом экспертом производится нумерация всех критериевпо убываниюстепениприемлемостинега-тивных последствий, связанных с данным критерием безопасности.Причем допускается,что эксперту не удастся различить между собой некоторые крите-рии.В этом случае при ранжировании он помещает их рядом в произвольном порядке.Затем проранжи-рованные критерии последовательно нумеруются. Оценка (ранг)критерия определяется его номером.

Если на одном месте находятся несколько неразличимых между собой критериев, то, обычно, оценка каждого из них принимается равной среднему арифметическому их новыхномеров[7]. Однако, представляется целесообразным несколько модифицировать такой метод оценки, приняв за ранг каждого из неразличимых критериев номер всей группы как целого объекта в упорядочении.

Таким способом могут быть оценены как степени влияния каждого параметра на частные критерии безопасности K_i , так и степени приемлемости последствий реализации угроз S_i . Например, пусть эксперт упорядочил критерии следующим образом:

Критерии, не различимые между собой, объединены в круглые скобки. Тогда оценки для каждого из критериев, вычисленные в соответствии с описанной выше процедурой, равны:

Применим нормирование по величине, равной сумме всех оценок:

R = ∑ Si i

В нашем случае R = 31. Таким образом, после линейного преобразования в шкалу [0; 1] по норме R получим:

Найденные предложенным способом оценки представляют собой обобщение системы весов Фишберна [8] для случая смешанного распределения предпочтений, когда наряду с предпочтениями в систему входят и отношения безразличия.

Полученный результат согласуется с хорошо известным в теории принятия решений фактом [5; 7; 9]: системе убывающего предпочтения альтернатив наилучшим образом отвечает система снижающихся по правилу арифметической прогрессии весов.

Угрозы, влияющие на безопасность системы, представляют собой набор неупорядоченных факторов одного уровня иерархии.

Влияние различных факторов на уровень комплексной безопасности может быть представлено в виде ориентированного графа G, имеющего одну корневую вершину и не содержащего петель и горизонтальных ребер в пределах одного уровня иерархии:

где { F_i } –множествофакторов(вершинграфа); { D_ij } – множество дуг,соединяющих i j

F ₀ = K – корневая вершина,отвечающая уровню комплексной безопасности в целом (интегральному критерию безопасности).При этом дуги расположены так,что началу дуги соответствует вершина нижнего уровня иерархии (ранга),а концу дуги – вершина ран-га,на единицу меньшего.

Примером такого графа,может служить четырехуровневый граф,в котором на нижнем,третьем уров- не расположены обозначенные через Ni негативные факторы,влияющие на безопасность системы и Zi – «демпфирующие» факторы,связанные с применением превентивных мер защиты и призванные ослабить влияние определенных угроз (негативных факторов). На уровень выше расположены обозначенные через Ui угрозы безопасности системы.На первом,пред-последнем уровне находятся частные критерии безопасности Ki .И,наконец,корневой вершине нулевого уровня соответствует комплексныйкритерийбезопас-ности K.

Следует заметить,что данный связный граф не яв-ляетсядеревом,посколькуневыполняетсятребование отсутствия простых циклов.Это обусловлено тем,что факторы,находящиеся на нижнем уровне иерархии, могут одновременно оказывать влияние на несколько факторов более высокого уровня.

Например, применение превентивных мер защиты от одной угрозы может одновременно с ослаблением негативных последствий этой угрозы усиливать или уменьшать влияние какой-либо другой угрозы. Или некоторые негативные факторы могут вызвать изменение сразу нескольких частных критериев безопасности (иногда в противоположном направлении).

Для дальнейшего построения модели комплексной безопасности системы на полученный граф необходимо наложить систему отношений предпочтения одних факторов другим по степени их влияния на заданный элемент следующего уровня иерархии:

E = {F i (e) F j | e >  ( > ; * )}, (1) где F_i и F_j – факторы одного уровня иерархии, > – отношение предпочтения, ≈ – отношение безразличия. Такая система может быть получена, например, изложенным выше способом нестрогого ранжирования.

Пример наложения системы отношений предпочтения типа (1) E = {N 1 >  N 2 ; N 2 > N ₃ ^ N 4 ; N 4 ~ N 5 } на фрагмент графа изображен на рис.1.

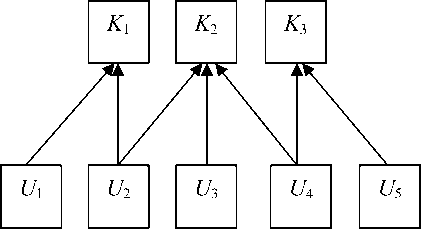
Рис. 1. Пример системы отношений предпочтения на одном из уровней иерархии

Остается ввести в рассмотрение набор качественных оценок уровней каждого фактора в иерархии:

L = {Очень низкий уровень (ОН),

Низкий уровень (Н), Средний уровень (С),

Высокий уровень (В),Очень высокий уровень (ОВ)}.(2)

Тогда,вкачестве математическоймоделиоцен-ки комплексной безопасности системы (KBS) может быть принят кортеж:

KBS =  .

Выводы

Полученное описание может быть использовано для построения показателя уровня комплексной безопасности компьютерных систем и сетей на базе агрегирования значений со всех уровней иерархии факторов на основе качественных данных об уровнях факторов и их отношениях порядка на одном уровне иерархии.

Применение модифицированного метода нестрогого ранжирования позволяет определить веса Фишберна для факторов одного уровня иерархии. При этом получено обобщение данных весов на общий случай предпочте-ния/безразличия факторов по отношению друг к другу.