Математическая модель контактного сопротивления холодного контакта при контактной точечной сварке

Практика контактной точечной сварки и многочисленные результаты опубликованных исследований однозначно подтверждают: одним из основных исходных условий получения качественных сварных соединений является оптимальность начального сопротивления контакта «деталь–деталь» r _КТ. Его величина и стабильность существенно влияет на размеры ядра, устойчивость процесса против образования выплесков и непроваров [1]. Вместе с тем до настоящего времени при разработке технологий контактной точечной сварки значение r _КТ определяют в основном экспериментально для конкретных условий сварки, однако это весьма трудоемко.

На основе проведенных исследований было сделано заключение о том, что из всех известных и исследованных в технологии машиностроения моделей шероховатых поверхностей для свариваемых контактов наиболее приемлема стержневая [2]. Тем более, что она наиболее просто и точно описывает механику контактного взаимодействия двух шероховатых поверхностей (рис. 1).

Согласно принятой модели контакта двух шероховатых поверхностей, проводимость в контактном слое осуществляется по nr числу единичных параллельных микропроводников диаметром d (d → 0) и длиной a, образующихся деформируемыми стержнями (микровыступами). Одну составляющую полного электрического сопро- тивления такого микроконтакта rКТ, которая обусловлена сопротивлением микропроводников в контактном слое, имеющих свойства, отличные от свойств основного металла, называют внутренним сопротивлением контакта rКВ. Другую же часть, которая обусловлена искривлением линий тока j в приконтактных областях (рис. 2), где можно допустить, что свойства основного металла не изменились, называют микрогеометрическим сопротивлением контакта rМГ. Тогда полное электрическое сопротивление контакта rКТ (Ом) будет равно сумме двух этих составляющих [3]:

^r КТ ^{= r} МГ ^{+ r} КВ^.

Полное внутреннее электрическое сопротивление кон- такта rВН (Ом) можно определить следующим образом:

^r ВН

r ВН         a         2 R max (1 - ε)

n r ρ^Δ n r Δ S ρ^Δ A r

где r _В^*_Н – внутреннее электрическое сопротивление единичного контакта, Ом; n_r – количество микроконтактов;

ρ_Δ – удельное электрическое сопротивление металла в контактном слое, Ом∙м; A_r – фактическая площадь контакта, м²; ε – деформации в контактном слое; R _max – наибольшая высота неровностей профиля, м; a – текущая толщина контактного слоя, м; Δ S – средняя площадь единичного контакта, м².

Для принятой модели микрогеометрическое сопротивление единичного контакта r ^*_МГ (Ом) можно определить по известной зависимости, с учетом его наличия в двух деталях (рис. 2):

* f 11 )

^ГМГ = ^2p I         I ,                   (3)

< d D )

где ρ – удельное электрическое сопротивление свариваемого металла, Ом∙м; d – диаметр цилиндрического микропроводника в контактном слое толщиной а , м; D – диаметр условного цилиндрического микропроводника вне контактного слоя, м.

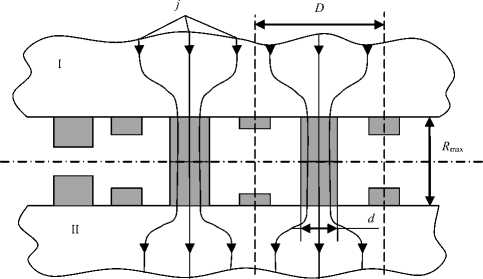
Рис. 2. Схема распределения тока по сечению свариваемых деталей для стержневой модели холодного контакта

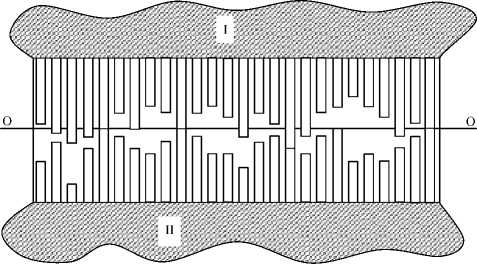
Рис. 1. Контакт двух шероховатых поверхностей. Стержневая модель чески. Например, при изменении Rmax в пределах 37^2,4 мкм значение аК /а02 и аСР /а02 (в скобках) при контактной точечной сварке деталей толщиной 0,5…4 мм из сталей 08 и 12 Х 18Р10Е, а также сплава АМг6 изменяется, соответственно, в следующих пределах: 2∙10–6…0,03 (1,6…1,9), 1,2∙10–5…0,02 (1,8…2,7) и 2,5∙10–5…0,4 (1,8…2,9). Для пластического контакта, по сравнению с упругим, задача определения его механических параметров значительно упрощается тем, что фактическая площадь контакта зависит только от микрогеометрии поверхности, а сближение зависит лишь от распределения материала в шероховатом слое [4]. Для этих условий значение деформаций е можно определить по зависимости [2]

е - I ° ^СР | v , (5) I ^Cе ■ ° 02 ■ ^Ь )

где С - коэффициент, учитывающий упрочнение металла в микронеровностях при их пластической деформации; b , v – параметры опорной кривой; σ₀₂ – условный предел текучести, Па. При условии контактирования двух одинаково шероховатых поверхностей параметры опорной кривой определяются по формуле [2]

b = k_Xi ■ 2 v^ b , ², v- 2 ■ v , , (6) где b ₁, v ₁ – параметры опорных кривых; k_{v 12} – коэффициент, учитывающий взаимосвязь параметров степенной аппроксимации кривой опорной поверхности.

Число микроконтактов n_r и их средний диаметр d можно определить, используя модель ситовой проводимости (рис. 3):

n _A _ Ac ■ П r ΔS2π Θε , d=

^{4Δ AC} = 22Θ ε ,

где A_C – контурная площадь контакта, м²; η – отношение фактической площади контакта к контурной площади контакта; Θ – комплекс, учитывающий влияние микрогеометрии поверхностей, м².

Полное микрогеометрическое сопротивление контакта r _МГ может быть определено по следующей зависимости [3]:

r _МГ

^Г МГ _ ^{2p f 1   1} ^

—— --- ■      1 I 1   " --- 1    " I

.

n_r   n r ( d D )

Для расчетов rВН и rМГ необходимо определить меха- нические параметры свариваемого контакта и, прежде всего, определить, какую деформацию претерпевают микровыступы, упругую или пластическую. Это можно сделать сравнением среднего давления аСР (Па), действующего в контурной площади контакта, с критическим давлением аК (Па), при котором контакт переходит в пластическое состояние.

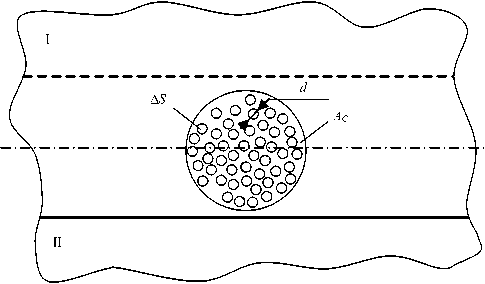
Рис. 3. Модель ситовой проводимости контакта

Сравнение значений а _С Р и а К при усилии сжатия электродов, определенных практикой режимов контактной точечной сварки деталей толщиной 0,5…4 мм из различных сталей и сплавов, показывает, что микронеровности в свариваемых контактах всегда деформируются пласти-

Среднее значение площади растекания линий тока от единичного микропроводника можно определить как площадь контактирующих микронеровностей к числу микроконтактов:

Δ A_С = ^A С ,                  (8)

n_r а ее диаметр D по след ующей зави симо сти:

_D= 4Δ A С _{= 2} 2Θ ε _{.           (9)}

πη

Пользуясь результатами проведенных исследований по изучению контактного сопротивления и проведя соответствующие математические выкладки с учетом (2, 4, 7–9), была получена зависимость для расчета сопротивления свариваемого контакта:

( 1 - Vn) . (10)

2^ СР R max ( 1 - ⁸ ). ПП _: V20 8

r _{КТ =} ρ_Δ    СР max        ₊ ρ СР

F _Эη           2 F _Эη

В зависимости (10) также учитывается влияние усилия сжатия электродов сварочной машины FЭ (Н) и среднего давления, действующего в контурной площади кон- такта σСР, на величину сопротивления свариваемого контакта.

Для практических расчетов r _КТ по данной зависимости необходимо знать величину р_д . Для ее определения необходимо экспериментально измерить величину r _КТ при любом F _Э (наиболее рационально измерять r _КТ при F _Э, близком к рекомендуемому, при контактной точечной сварке данных деталей), а затем рассчитать величину р_д по следующей зависимости, полученной из (10):

рд =____Fnх

^А 2° СР R max ( 1 - 8 )

поср V20 8 (

• х ГКТ - Р--------(1 - Vn ) .

• 2 Fa П

Разработанная математическая модель позволяет по минимальному количеству экспериментальных замеров определить весь диапазон изменений контактного сопротивления холодного контакта для выбранных режимов контактной сварки. Расчеты, полученные с использованием разработанной модели, с точностью, достаточной для технологического применения, описывают поведение электрического сопротивления в контакте «деталь–деталь» R _Д и «электрод–электрод» R _Э, о чем свидетельствуют экспериментальные и расчетные значения этих сопротивлений (рис. 4).

Применение данной модели определения контактного сопротивления позволяет повысить производительность при разработке технологических процессов контактной сварки без трудоемкого определения контактного сопротивления экспериментальным путем для конкретных условий протекания процесса сварки.

R , мкОм

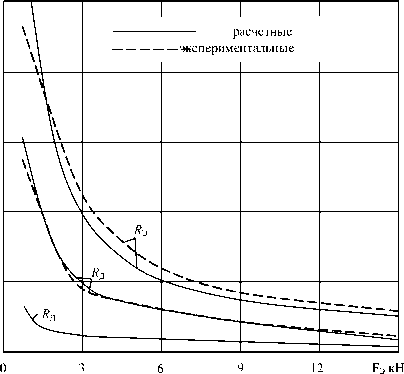
Рис. 4. Результаты экспериментальных и расчетных значений сопротивлений в контакте «деталь–деталь» R _Д и «электрод– электрод» R _Э, в зависимости от усилия сжатия электродов сварочной машины F _Э