Математическая модель квалиметрии факторных кластеров, влияющих на формирование характеристик многопараметрических социальных объектов (на примере инженерно-технических работников машиностроительных предприятий)

сформированности определенных социальных характеристик. Такая фундаментальная проблема исследования поставлена впервые.

В рамках решения этой проблемы разработаны аксиоматический базис модели типизации МСО в процессе социализации в условиях внешней неопределенности [2], выявлен принцип построения матрицы соответствия ее параметров [1], а также математическая модель ква-лиметрии объектов процесса социализации [3]. Однако многообразие факторов социализации МСО затрудняет использование этих моделей, поэтому в целях оптимизации их практического применения возникает необходимость кластеризации системы анализируемых факторов.

Теоретико-методологические основы формирование модели. Аксиоматический базис, представленный в работе [2], формирует следующую систему основных понятий модели типизации МСО в процессе социализации в условиях внешней неопределенности. Существует некоторое n -мерное ( n →∞) информационное пространство N, определяющее совокупность факторов, воздействующих на МСО, m -мерное ( m →∞) информационное пространство M , определяющее множество факторных кластеров, оказывающих суперпозиционное синергетическое воздействие на него, и l -мерное ( l →∞) информационное пространство L, определяющее множество социальных характеристик МСО. m -мерное

( m ^ю) информационное пространство M и l -мерное ( l →∞) информационное пространство L являются подмножествами n -мерного ( n ^да) информационного пространства N . Элементами информационных пространств N, M и L являются информационные параметры (аргументарно-факторные и функционально-резуль-тирующие) процесса социализации индивида в современном обществе. Необходимость формирования информационного пространства M факторных кластеров обусловлена значительным числом факторов процесса социализации МСО и сложностью анализа влияния каждого из них на формирование социальных характеристик объекта.

Существуют множества D, A и B, элементами которых являются, соответственно, факторы Di, i = 1: n, непосредственно воздействующие на МСО, факторные кластеры Aj, j = 1: m, оказывающие суперпозиционное синергетическое воздействие на МСО, и социальные характеристики МСО Bk, к = 1: l, которые он приобретает в результате реализации процесса социализации. Каждая i-я, i = 1: n ось ONNi (луч [ONNi) пространства N отображает воздействие фактора Di, i = 1: n. На луче [ ONNi)  определен единич ный вектор eNi с началом в точке ON. Если точка Dpi е [ONNi), то вектор ONDpi = qpi" eNi, где qpi -координата вектора ONDpi на оси ONNi, интерпретируемая как степень воздействия фактора Di, i = 1: n, на p-ой МСО. Каждая j-я, j = 1: m ось OMMj (луч [OMMj)) пространства M отображает воздействие кластера факторов  A;, j = 1: m. На луче [OMMj) определен единичный вектор eMj с началом в точке OM. Если точка Apj е [OMM), то вектор OMApj = spj • eMj, где Spj -координата вектора OMApj на оси OMMj, интерпретируемая как степень воздействия кластера факторов A;, j = 1: m, на p-ом объекте (МСО). Каждая к-я, к = 1: l ось OLLk (луч [OLLk) пространства L отображает сформированность социальной характеристики МСО Вк, к = 1: l. На луче [OLLk)  определен единичный вектор eLk с началом в точке OL. Если точка Bpk е [OLLk ), то вектор OLBpk = hpk ■ eLk , где hpk - координата вектора OLBpk на оси OLLk, интерпретируемая как уровень сформированности социальной характеристики Bk, k = 1: l p-го МСО.

Множество факторов, воздействующих в процессе социализации на p -й МСО, отображается в n -мерном информационном пространстве N точкой ^Np ^{( q}p 1 ; q p 2; — q pr ;•••; q pn ) , где q_pr -проекция точки N_p на ось O_NN_r , r = 1: n . Каждая i- я, i = 1: n ось O_NN i имеет количественную неотрицательную шкалу значений, т.е. каждая точка q i на i- й оси соответствует определенной степень воздействия фактора D i на анализируемый МСО. В частности, значение q_pr=0 означает, что на p -й МСО не осуществлялось воздействие фактора D r , r = 1: n , а значение q_pr ^G означает, что на p -й МСО фактор D r оказывал влияние.

Для последующего анализа значений q i , i = 1: n , целесообразно установить пороговый q ^m'ⁿ i , продвинутый q^v i и высокий q" i уровни воздействия фактора D i . Значение q_pi , при котором q pi ^ q w , подразумевает, что на p -го МСО фактор D r оказал сильное воздействие. Совокупное воздействие на p- й МСО всех факторов со-циализационного процесса X_p функционально зависит от значений всех координат точки N i , i = 1: n , информационного пространства N :

X p    F 1 ⁽q p 1 ; q p 2 ; •••; q pr ; ••• q pn )

В случае, когда на p -й МСО не воздействовал фактор D r , r = 1: n , выражение (1) примет вид:

X p = F ⁽ q p 1 ; q p 2 ;-; q

pr - 1 ^{; 0;} q pr + 1 ^; ••• q pn )

Каждая j-я, j = 1: m ось OMM; имеет количественную неотрицательную шкалу значений, т.е. каждая точка s; на j-й оси соответствует совокупной степени воздействия факторного кластера A; на МСО. В частности, значение spw=0 означает, что на p-й объект воздействие со сто роны факторного кластера Aw, w = 1: m , отсут ствует, а значение spw^G означает, что на p-й объект было оказано совокупное синергетическое воздействие со стороны факторного кластера Aw.

Совокупная степень воздействия со стороны всех факторных кластеров на p-й объект (МСО) отображается в m-мерном пространстве M точкой Mp(sp 1; sp2; ••• spw; •••; spm), где spw - проек ция точки Mp на ось OMMw, w = 1: m .

Для последующего анализа значений s ; , j = 1: m , целесообразно установить пороговый s m™ j , продвинутый s' "j и высокий s^w j уровни воздействия со стороны факторного кластера A j .

Значение s pj , при котором s pj ^ s w j , подразумевает, что на p -й объект было оказано воздействие высокого уровня со стороны факторного кластера A j . Совокупное синергитеческое суперпозиционное воздействие Y_p со стороны всех факторных кластеров на анализируемый p -й МСО функционально зави сит от значений всех координат точки M j , j = 1: m информационного пространства M :

функционально детерминирована значениями совокупного воздействия X p на него всех факторов D i , i = 1: n , социализационного процесса, т.е.:

Y p =^ ( X p )

Y p = F 2 ⁽ s p 1 ; s p 2 ;

^; s pw ^; '•• s pm )

В случае, когда на p -й МСО воздействие факторного кластера A w , w = 1: m , не осуществлялось выражение (3) примет вид:

^Yp   ^F2 ⁽s p 1 ^; s p 2 ^; ••• ^; s pw - 1 ^{; 0;} s pw + 1 ^; ••• s pm )

Отсюда следует, что степень воздействия S j факторного кластера A j , j = 1: m функционально зависит от значений всех координат q i , i = 1: n , точки N i информационного пространства N , которые характе риз уют степень воздействия факторов D i , i = 1: n , входящих в анализируемый факторный кластер A j , в виде:

^s ₇ = f ⁽ q i ; q 2 ;-; q , ;••• q n )

В случае, когда фактор D r , r = 1: n не входит в состав факторного кластера A j , j = 1: m выражение (5) примет вид:

^s ₇ = f ⁽ Q 1 ; q 2 ; •••; Q r - 1 ; °; Q r + 1 ; ••• Q n )

Пусть на p -й МСО воздействует совокупность факторов D i , i = 1: n , степень воздействия которых отображается в n -мерном информационном      пространстве      N     точкой

Np(qp 1; qp2; ••• qpr; •••; qpn). Для каждого фактора Di, i = 1: n установлены значение qm, называемое пороговым значением для фактора Di, такое, что если на p-й МСО оказывается такая степень воздействия qpi фактора Di, что выполняется условие qpi ^ qi , то воздействие фактора Di на p-й объект считается незначительным, и в этом случае полагают, что qpi=0. Пусть совокупный уровень воздействия факторного кластера Aj,  j = 1: m, определяется подмножеством факторов Djg с{d,}, i = 1: n, g = 1: t (рис. 1). Оценка синергетического воздействия на p-ый МСО этого подмножества факторов осуществляется на основании следующей модели квали-метрии факторных кластеров. Пусть каждый фактор Djg имеет уровень значимости ajg, g = 1: t, который показывает, какую долю анализируемый фактор Djg привносит в совокупное воздействие на МСО той части т-мерного

(т^да) информационного пространства M, которая составляет факторный кластер  Aj, j = 1: m .

Кроме того, совокупная степень воздействия Y_p всех факторных кластеров на p -й МСО, также

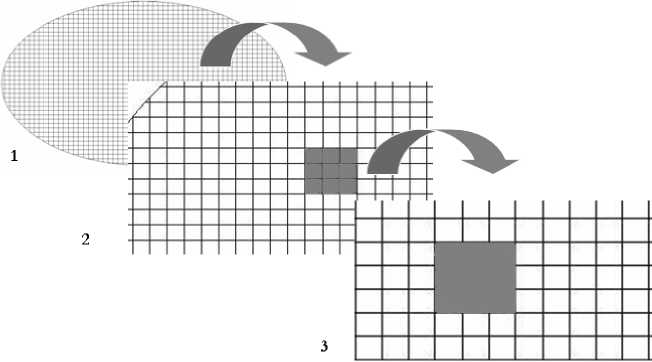
Рис. 1. Модель формирования т -мерного ( т ^да) информационного пространства M множества факторных кластеров A j (позиция 3) на базе n -мерного (п^да) информационного пространства N (позиция 1) совокупности факторов D i (позиция 2)

Для каждого фактора Djg, g = 1: t, входящего во множество   Djg с {Di}, i = 1: n, g = 1: t, с уровнем значимости ajg, g = 1: t, в составе факторного кластера Aj, j = 1: m, обладает следующими свойствами:  0 ^ «jg ^ 1 и t

Z agj = 1. Совокупная степень воздействия фак-g=i торного кластера Aj, j = 1: m на МСО может определяться несколькими способами, например:

-

по уровню максимального значения сре- ди всех имеющихся значений степени воздействия факторов, входящих в совокупность Djg с {Di}, i = 1: n, g = 1: t и определяющих совокупную степень воздействия факторного кластера Aj, j = 1: m, т.е.:

s pj = max // jg • q pjg ; g = 1: t ^} (8)

-

по уровню минимального значения среди всех имеющихся значений степени воздействия факторов, входящих в совокупность Djg с {Di}, i = 1: n, g = 1: t и определяющих совокупную степень воздействия факторного кластера Aj, j = 1: m, т.е.:

s pj = min ^ jg • q pjg ; g = ^1: t ^} (9)

-

по уровню достижения среднего значе- ния среди всех имеющихся значений степени воздействия факторов, входящих в совокупность Djg с {Di}, i = 1: n, g = 1: t и определяющих совокупную степень воздействия факторного кластера Aj, j = 1: m, скорректированного по уровню значимости αjg для каждого фактора Djg, входящего в состав факторного кластера Aj, и рассчитываемый по формуле средней арифметической взвешенной, т.е.:

spj

t

Z а jg • qpjg

g = 1

t

Уровень значимости αjg для каждого фактора мини-уровня Djg, g = 1: t, входящего в состав факторного кластера Aj, j = 1: m, определяется экспертно-аналитическим путем (например, с применением системы поддержки принятия решений Expert Decide 2.0) с учетом сложившейся в анализируемый период времени социо- динамики внешней среды и суперпозиционного воздействия на МСО со стороны макро- и мезофакторов, образующих по отношению к анализируемому объекту систему «условий внешней неопределенности».

Таким образом, с помощью выражений (8)-(10) решается проблема установления количественной зависимости между степенью воздействия S j факторного кластера A j , j = 1: m от совокупности координат q i , i = 1: n точки N i информационного пространства N , характеризующих степень воздействия каждого фактора на многопараметрический социальный объект. Такая зависимость может быть представлена в общем виде:

s j = f ⁽ q 1 ; q 2 ;-; q i;- q n )

Специфика применения модели. Процедуру кластеризации факторов социализации МСО целесообразно рассматривать в рамках реализации ее определенного подпроцесса. В качестве примера, рассмотрим процедуру кластеризации факторов такого подпроцесса как профессиональная социализация. В этом случае в качестве МСО могут рассматриваться выпускники вуза/колледжа, в качестве системы социальных характеристик – совокупность их социально-профессиональных компетенций, в качестве факторов и факторных кластеров, их формирующих – систему знаний, умений и навыков, приобретаемых студентом в ходе освоения системы дидактических единиц и учебных дисциплин, составляющих основную образовательную программу (ООП) направления подготовки специалистов. При этом каждая дидактическая единица фактора Djg, g = 1: t, входящая во множество дидактических единиц, определяемых основной образовательной программой направления подготовки специалистов Djg с {Di},i = 1: n, g = 1: t, имеет уровнем значимости ajg, g = 1: t, при формировании системы знаний, умений и навыков в рамках каждой учебной дисциплины Aj, j = 1: m . Значение величины ajg, g = 1: t целесообразно определять экспертным путем при разработке рабочих программ учебных дисциплин и контрольных измерительных материалов по учебным дисциплинам, т.к. это позволит в дальнейшем определить и степень влияния каждой дидактической единицы, и каждой учебной дисциплины на уровень сформированности компетенции выпускника, а, в целом, оценив компетенции выпускников, выявить, например, к выполнению должностных требований какого типа инженерно-технического работника (инженер, инженер-технолог, инженер-конструктор и т.д.) машиностроительного предприятия наиболее адаптирован молодой специалист [4].

Выводы и рекомендации: модель квали-метрии факторных кластеров, являясь компонентом математической модели квалиметрии, типизации и идентификации МСО, может быть положена в основу разработки общего аналитического макроса, предназначенного для автоматизации исследовательских задач процесса социализации МСО. Кроме того, она имеет универсальный характер и применима для анализа различных подпроцессов социализации (профессиональная социализация, политическая социализация, экономическая социализация и т.д.)

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 13-0100147 а.