Математическая модель линии задержки

В [1] рассматривались некоторые элементы математического описания переменных x и ука- зателей ^ в виде пар чисел (с; x). В этой работе были рассмотрены такие элементы (объекты), как одномерный массив и очередь, а также операции, которые могут выполняться над рассматриваемыми объектами. В радиотехнических задачах часто применяется такой элемент как линия задержки (ЛЗ). Реализация данного объекта на базе вычислительной техники достаточно проста. Однако существует несколько вариантов реализаций это- го объекта. Целью данной работы является математическое описание объекта линии задержки и описание вариантов ее реализаций. Кроме того, предлагается формализовать некоторые операции, которые производятся с линией задержкой, например запись некоторого значения в линию задержки.

Математическая модель линии задержки

Линия задержки представляет собой одномерный массив данных. Поэтому для нее определены действия, подобные операциям, применимым к одномерному массиву [1].

Однако для ЛЗ существуют понятия входной ячейки – ячейка, индекс которой равен 0, и выходной ячейки, индекс которой равен i _max .

Если в локальной области памяти расположена только 1 ЛЗ, то максимальное значение индекса можно определить как i= max i. max max    ςi ≠-1

Создание ЛЗ размером в N элементов – установление адресов, взятых из локальной области памяти, для N пар ( с ; d ) (переход от -1 к реальным адресам), например

S i ^ i , i = 0, N -1 или i = 0, imax .

Обозначение ← является оператором записи значения в переменную или указатель; i _max – максимальное значение индекса; стрелка вверху показывает порядок изменения переменной i .

Удаление ЛЗ – установка признака отсутствия адреса для всех пар (с ; d ) , образующих массив (переход от реальных адресов к -1 )

• с. ^--z — 0, i ^i ,           , max

Взять адрес ячейки ЛЗ

Получить значения по адресу ячейки ЛЗ с индексом i

di ^* (Si).

Получить значение элемента массива с индексом i

y← di или y← dςi .

Если в локальной области памяти расположена только 1 ЛЗ, то максимальное значение индекса можно определить как i← max i.

max max      ςi≠-1

Получить размер ЛЗ с индексом i

N ^ size (d ) = 1 + imax .

Операция циклического сдвига

Ее можно представить в виде

_r ^{(k +1)} _ _r(^k)       ^k+1) _ ,/0)    ; —         _ 1

^S i +1       S i ,    d i +1       d i , i 0, i max 1,

' c(k+1) = c(k)    ^k+1) = ^k)       , = /

tS0        Si ,   d0 di ,       i imax, или

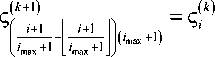
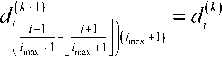
7 = 0,7

’ max здесь ⎢⎣⋅⎥⎦ – операция «округления вниз» до целого числа (отбрасывание дробной части числа), d0← увх;

выражение

⎛_⎜ i + 1

^⎜ ⎝ ⁱ max ^{+ 1}

max

( i max ⁺ 1 ) ^-

выпол-

няет задачу нахождения остатка от целочисленного деления. В языке С, такая операция обозначена символом «%».

Важно обратить внимание,что циклическое переобозначение осуществляется за 1 шаг при перехо-деот момента времени k к k + 1 .При циклическом сдвиге в реальной программе происходит только изменение значения указателя на входную ячейку.

Операция записи в ячейку с номером i для ЛЗ отсутствует.

Операция сдвига и записи входного значения y _вх во входную ячейку ЛЗ. Здесь существует несколько вариантов реализации. Ниже приведены 3 основных варианта.

1. d ■ ^ d ._j max           max

0,7

’ max

^^^^^^—

¹ , d o ^ У вх

Здесь после выполнения действия не сохраняется соответствия d ↔ς, так как значения переменных перезаписываются по другим адресам:

d ^{( k + 1)} = d^ )    / = 0,/ — 1

i              i + 1 ’              ’ max ’

C ^{( k + 1 )} = c^(k )     i = o"/ "

^i         ^i ’ ¹    ,’ ‘max •

В этом случае число записей при выполнении операции сдвига растет пропорционально росту размера ЛЗ.

• 2.    При использовании локальной памяти с бесконечной адресацией с сохранением соот-

• ветствия при сдвиге ЛЗ, размером в N элементов, должна быть создана следующим образом

Qi ^ N -1 - i, i = 0,N-1или i = 0,^ .

В этом случае операция сдвига и записи входного значения y вх во входную ячейку ЛЗ производится с помощью следующих действий

⁽ k + 1 )

S o    ^ k ⁺ i max ^{+ 1} ,

( ^{k + 1} )

d0   ^ УвХ ,

⁽ k + 1 )

4ax +1 ^

d(k+1) =

Здесь число записей при выполнении операции сдвига не зависит от размера ЛЗ. Однако при каждом считывании входного значения все адреса ячеек ЛЗ неограниченно увеличиваются на 1.

• 3.    Для ЛЗ, использующей циклическую адресацию d^ ¹ ) = d( k ) , i = 0, i max - 1 ,

  

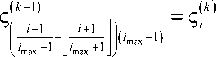
Здесь число записей при выполнении операции сдвига не зависит от размера ЛЗ. При этом запись новых адресов не происходит.

Обозначение некоторых действий надЛЗ в виде операторов и функций

Для ЛЗ d операция записи входного значения y _вх во входную ячейку ЛЗ обозначим как

d ^ Увх , где ^ - оператор записи результата, выдаваемого одним объектом, в другой объект.

Операцию считывания значения из ЛЗ (из выходной ячейки ЛЗ) и запись в переменную yвых обозначим как у ^ d .

вых

Операцию циклического сдвига в ЛЗ без записей в ЛЗ обозначим в виде функции

shift (d).

Операция создания ЛЗ

[ n new (d[ 11.

Операция удаления ЛЗ

del (d).

Выводы

При описании алгоритма работы радиотехнического объекта, включающего ЛЗ, при операциях записи и считывания данных можно использовать вышеприведенные обозначения.

Кроме того, если алгоритм подразумевает создание новых объектов ЛЗ или их удаление (что может быть использовано в объектно-ориентированных программах), то этот процесс также может быть кратко записан с помощью вышеприведенных обозначений.