Математическая модель машинно-тракторного агрегата на базе трактора с гидростатической трансмиссией

Введение и цель работы. При определении показателей работы машиннотракторных сельскохозяйственных агрегатов (МТА) в настоящее время применяют данные типовых тяговых характеристик тракторов, полученные в результате их испытаний при постоянном тяговом сопротивлении. В действительности же МТА подвергается внешним воздействиям, носящим динамический характер [1, 3, 5-9].

Стохастический характер внешних воздействий существенно отражается на показателях работы агрегатов [1, 5, 8, 9].

Возникающие при эксплуатации МТА случайные колебания тяговой нагрузки, амплитуда которых достигает 30-40% от её среднего значения, являются следствием воздействия на движители трактора неровностей поля, неравномерности взаимодействия рабочих органов сельскохозяйственных машин с почвой и т.д. Такой характер динамического воздействия вызывает изменение работы двигателя, колебания остова, повышенное буксование движителей, что приводит к снижению показателей работы МТА.

Существуют различные способы уменьшения влияния колебаний тяговой нагрузки на выходные показатели МТА [3, 4, 5, 7]. Одним из них является применение гидростатической передачи, основной недостаток которой специалисты видят в пониженном КПД её по сравнению с механической. Однако использование механического привода в реальных условиях эксплуатации не позволяет использовать максимально возможную энергию двигателя внутреннего сгорания (ДВС). Этот «генетически» присущий шестеренной передаче фактор (своего рода «шаг квантования») закрывает проблему КПД гидростатической передачи.

В Азово-Черноморском инженерном институте ФГБОУ ВО Донской ГАУ разработана схема гидростатической трансмиссии сельскохозяйственного мобильного энергетического средства (рисунок 1).

Проверка эффективности работы МТА на базе мобильного энергетического средства (МЭС) с гидростатической трансмиссией экспериментальным путём сложна, дорогостояща и требует большого количества времени. Поэтому целесообразно провести аналитические исследования с целью оценки влияния гидростатической трансмиссии на энергетические и другие показатели МТА при неустановившихся режимах нагрузки, которые характерны в реальных условиях эксплуатации [1,2, 10].

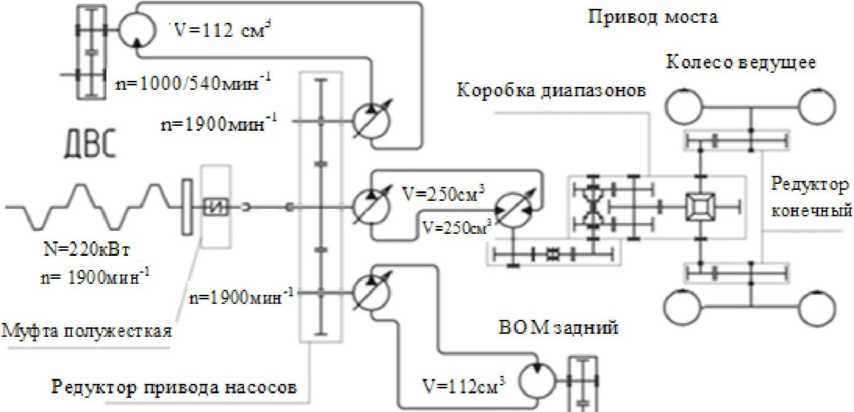
п= 1000/5 40mhh^j

Рисунок 1 - Схема приводов силового вращательного движения мобильного энергетического средства

Поэтому целью работы является создание математической модели машиннотракторных агрегатов на базе энергетических средств с гидростатической трансмиссией.

Исходные данные для разработки модели. При математическом моделировании МТ А рассматривают как динамическую систему, состоящую из элементов и звеньев. Движение составляющих динамической системы происходит под действием различных возмущающих и управляющих факторов, которые могут быть описаны математическими функциями [1-5, 10].

Трансмиссия мобильного энергетического средства - динамическая система, состоящая из вращающихся масс с различными упругими и демпфирующими связями.

Для аналитических исследований движения МТА составляют динамическую модель, в которой поступательные и вра щающиеся массы агрегата заменяют маховиками, моменты инерции которых выбираются из условия равенства их кинетической энергии и заменяемых масс агрегата [1, 2, 3, 5, 6].

Сельскохозяйственный МТА на базе мобильного энергетического средства с гидростатической передачей в трансмиссии нами рассматривается как динамическая модель (рисунок 2), в которой массы с моментами инерции Ji заменяют движущиеся детали двигателя, J_MC - вал муфты сцепления, J2 - детали привода насоса гидростатической передачи, J; и J4 - колёса МЭС и т_с - поступательно движущиеся массы агрегата.

МТА представлен последовательно соединёнными звеньями: двигатель - силовая передача - ведущее колесо - нагрузка, с отображением упругих и демпфирующих связей между ними.

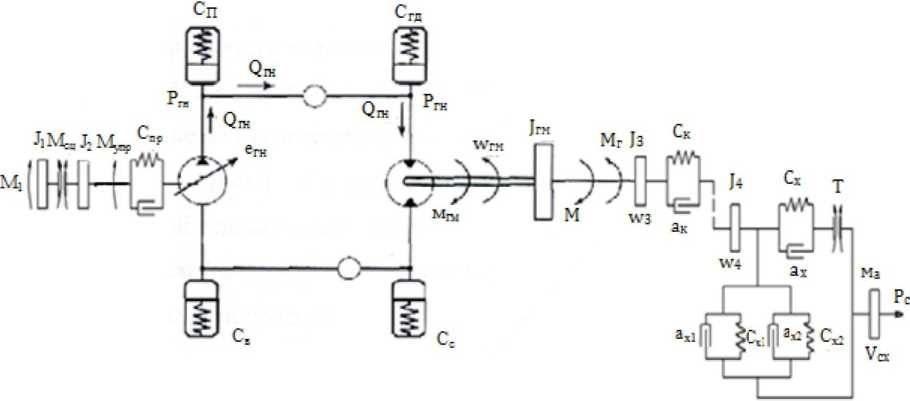
Рисунок 2 - Схема динамической модели МТА на базе трактора с гидростатической трансмиссией

При составлении модели были сделаны следующие основные допущения:

• -    рама МЭС с агрегатами, закреплёнными на ней, представлена как твердое тело;

• -    колебания звеньев системы определяются от начала координат в центре масс МЭС;

• -    МЭС сохраняет прямолинейное движение;

• -    упругие связи между звеньями представлены с линейной характеристикой;

• -    воздействия на правые и левые колеса приняты одинаковыми;

• - силы вязкого трения в звеньях динамической системы приняты пропорциональными относительным скоростям, а силы неупругого сопротивления - усилиям.

Материалы и методы исследования. Поведение динамической модели МТА на базе мобильного энергетического средства с гидростатической трансмиссией определяется углами поворота элементов системы фі (фі - коленчатого вала двигателя, ф_мс - вала муфты сцепления, фз - вала привода насоса гидростатической передачи, фгм - вала гидромотора, фз - оси ведущего колеса, ф4 - беговой дорожки шины) и положением в агрегатах.

Так как силовые установки современных мобильных энергетических средств имеют всережимные регуляторы и турбонагнетатели, нами к вышеобозначенным параметрам динамической системы добавлены координаты положения рейки топливного насоса z и угла поворота ротора турбонагнетателя ф_н [2, 3].

Производные от обобщенных координат по времени представляют собой обобщенные скорости соответствующих элементов и звеньев динамической системы агрегата.

Движение МТА происходит под действием крутящего момента, развиваемого двигателем Mi, момента трения между ведущими и ведомыми дисками муфты сцепления М_сц, моментов упругих сил связи, возникающих в трансмиссии мобильного энергетического средства М_упр и М_у, момента от окружной деформации шины М_шк, момента, обусловленного упругостью и демпфированием в шине М_ш, усилием в контакте отпечатка шины с опорным основанием тфй,) и усилием сопротивления рабочих органов при работе машины р_с [2, 3].

В представленной динамической модели учитывается сухое и вязкое трение в элементах системы, жесткости трансмиссии и шины, буксование движителей коэффициентами а_тр, а_к, a_z, а_х, с_тр, с_к, c_z, с_х и б. Математическая модель двигателя нами представлена в следующем виде [2, 3, 5]:

J,-d>, = avcx^av(D^civz -Мт

^Jh"®_h =в₁-Ю₁ + в₂-Ю_н+в_э- Z , т -z + ^-z + c₁-z=c₂-o₁.

где со 1, со„ — угловые скорости соответственно коленчатого вала и ротора турбонагнетателя двигателя;

т_р - масса всережимного регулятора двигателя;

J„ - момент инерции турбонагнетателя двигателя;

аі, аз, аз, ві, вз, вз - экспериментальные коэффициенты;

Р - коэффициент вязкого трения;

ci, сз - коэффициенты, определяемые экспериментально.

В начальный период разгона агрегата, когда имеется разность угловых скоростей ведущего coi и ведомого соз дисков, моментом сопротивления М_с движению МТА является момент трения муфты сцепления М_сц. Значение момента трения между дисками муфты сцепления с достаточной степенью точности описывается зависимостью [2, 3, 5]:

где п - количество пар поверхностей трения между дисками муфты сцепления;

Р_пр - максимальное усилие, создаваемое пружинами муфты сцепления;

А? - средний радиус дисков муфты сцепления;

t - время включения муфты сцепления; ki, кз - показатели, полученные экспериментальным путем;

Лмах, ^И - максимальное значение и относительное изменение коэффициента трения между дисками сцепления.

Движение механической передачи привода гидравлического насоса мобильного энергетического средства с гидростатической трансмиссией определяется, в том числе, коэффициентами жесткости С_тр и вязкого трения а_тр.

Движение масс привода гидравлического насоса мобильного энергетического средства с гидростатической трансмиссией на основе разработанной динамической модели опишется уравнением:

J2-^=^4^ + <^2X

где d_mp-a)2 - параметр, определяющий потери энергии на вязкое трение при равномерном вращении деталей привода гидромотора.

Значение момента М_упр зависит от угла закручивания вала привода гидромотора. Применительно к рассматриваемой динамической модели имеем:

М = С -ф + а • (ар — о ) упр тр ттр тр \ 2 гн; .

Уравнение (5) в окончательном варианте можно представить в следующем виде:

^J₂ •            - (С_тр • ф_тр + а_тр • (щ₂ - щ_гн) + а_тр

Объемная гидростатическая передача с регулируемым гидравлическим насосом (0 < егн < 1) и нерегулируемым гидравличе ским мотором (егн = 1) с достаточной степенью точности описывается дифференциальными уравнениями (8-12):

(jp-J Ya> =ГС + tz -со ) + tzz -соЛ-е -V-----р \ 2 гм/ гн тр т тр тр \ 2 гн; тр 2-1 гн н<

Г)2 -О2

Р гн Р гм 'Рм’

Q = е -V -со •;

гн гн гн р„ = 4 + т;*—

О»)

ОО

где Ji - приведенный к валу насоса момент инерции подвижных частей гидронасоса;

Jzm - приведенный к валу гидравлического мотора момент инерции его подвижных частей;

Огм - угловая скорость вращения вала гидравлического мотора;

р_гн - давление рабочей жидкости на выходе гидравлического насоса;

Ргм ~ давление рабочей жидкости на входе гидравлического мотора;

е_гн - параметр регулирования гидравлического насоса;

Угн - рабочий объем гидравлического насоса;

F„ - площадь поперечного сечения трубопровода;

Q₂h, Qzm - расходы рабочей жидкости на выходе гидравлического

насоса и на входе в гидравлический мотор;

Пмгн, Пмгм ~ механические коэффициенты полезного действия гидравлического насоса и гидравлического мотора;

Логн, Логм ^- объемные коэффициенты полезного действия гидравлического насоса и гидравлического мотора, учитывающие внутренние утечки жидкости в гидравлических машинах;

к_с - коэффициент, учитывающий потери на трение при турбулентном потоке;

р_м - плотность рабочей жидкости гидростатической передачи.

При движении колесного движителя в ведущем режиме под действием веса мобильного энергетического средства, силы сопротивления перекатыванию и крутящего момента, прилагаемого к оси колеса, оболочка шины испытывает различные деформации. Шину можно представить двухмассовой динамической моделью, в которой маховик с моментом инерции J3 заменяет обод колеса и часть шины, а маховик с моментом инерции J4 - беговую дорожку шины.

Динамику ведущего колеса мобильного энергетического средства можно описать следующей системой дифференциальных уравнений [3, 4, 5]:

-i —М

3    3 упр тр шк

-tb^ =мшк -мш.

Момент упругой связи Му в механической передаче от вала гидравлического мотора к оси ведущего колеса может быть рассчитан по зависимости

^Му = С_тр • к<Ргм ~ imp • Фз )+ «тр ' few "  ^р ' Фз У^М ' ^Э^гм " Ітр ' Фз )

где

і_тр - передаточное число механической передачи силового потока от вала гидравлического мото

вала гидравлического мотора к оси ведущего колеса;

М - момент сухого трения в силовой

ра к оси ведущего колеса;                  передаче от вала гидравличе- стр - жесткость силовой передачи ва-             ского мотора к оси ведущего ла от гидравлического мотора к             колеса.

оси ведущего колеса;                  Момент сухого трения передачи фгм, фз - соответственно углы энергии от вала гидравлического мотора к поворота вала гидравлического оси ведущего колеса мобильного энергети-мотора и оси ведущего колеса; ческого средства определяется по формуле атр - коэффициент демпфирования передачи силового потока от

М = Стр • ^Ф™ "Ітр • Фз)' ^"ЛтрХ где

Лтр ~ КПД силовой передачи.           шины, рассчитать можно по следующей

Момент, возникающий от закрутки зависимости [3, 4, 5]:

Мшк = Ск2 • {(Рз - ^4)+ «К2 • («3 - ^4) , где сК2, аК2 - коэффициенты, характеризующие жёсткость и демпфирование колеса в окружном направлении.

Момент М_ш, связанный с упругостью и демпфированием в шине, можно определить по зависимости [3, 4, 5]:

Мш = (cx-x + ax-x)-rd+R-a2, где сх ,ах - коэффициенты, характеризующие продольную жесткость и вязкое трение в шине;

а - смещение результирующей реакции R опорного основания относительно центра вращения колеса;

га - динамический радиус качения ведущего колеса.

Так как центр ведущего колеса при движении из-за продольной деформации шины смещается в противоположную движению сторону, нами тангенциальная жесткость пневматической шины, включаемой обычно при моделировании в жёсткость всей силовой передачи, заменена продольной жесткостью сх [3]. Смещение оси ведущего колеса тем больше, чем выше толкающая сила Т колеса, которую можно определить по зависимости [3, 4, 5]:

Т = Сх "х + ах " х.

При увеличении плеча вертикальная нагрузка на ведущее колесо и реакция опорного основания создают дополнительный момент сопротивления перекатыванию [3, 4].

аш = / • Гс +

Смещение оси ведущего колеса а^ в зависимости от деформации шины х можно с достаточно высокой степенью точности определить по формуле сх • х + ах • х

Cz                                        (15)

где / - коэффициент сопротивления каче-       Результирующую вертикальную ре нию движителя в свободном ре- акцию опорного основания на ведущие ко-жиме;                           леса можно определить по зависимости гс - радиус качения движителя в свободном режиме.

Rx=c-z+a-z+c-zr,

2 z ш z ш z О                                            ( 10 )

где c_z - радиальная жёсткость шин движителей мобильного энергетического средства;

a_z - коэффициент вязкого трения в радиальном направлении шин движителей мобильного энергетического средства;

гш - деформация шины движителя, обусловленная колебаниями остова мобильного энергетического средства;

zo - статическая деформация шины движителя.

Динамический радиус ведущего колеса определяется как расстояние от оси движителя до опорного основания:

В связи с имеющимися неровностями опорного основания и колебаниями тягового сопротивления при работе сельскохозяйственного агрегата возникают колебания мобильного энергетического средства как в продольной, так и в вертикальной плоскости. Тогда движение МТ А можно описать системой дифференциальных уравнений [3]:

^тс¹ z_c = c_zi • k " 7i)+«_zi • k "7і) + ^c_z2 • k - 7₂) + «_z2¹ k "7₂);

J=' Фе = ki' k " 7i) + «_zi• k - 7JL «- k₂ • k - 7₂)+«_z2 • k - 7₂)Г b +

+k₂ • -c + ^₂ -^L k + ^һсУ^рс • ^h=;

mc'Vo;=Cx-X ^«xX -Pc~mc' S-ф^

где J_c - приведённый к центру масс момент инерции мобильного энергетического средства;

z_c - вертикальное отклонение центра масс мобильного энергетического средства от равновесного состояния;

Ф= - продольный угол поворота остова относительно центра масс мобильного энергетического средства;

zi, Z2 - вертикальные отклонения от равновесного состояния центров масс ведущих мостов мобильного энергетического средства;

Чь 42 - координаты микронеровностей опорного основания под передними и задними колёсами мобильного энергетического средства;

а, b - координаты переднего и заднего мостов от положения центра масс мобильного энергетического средства;

h_c - координата вектора силы тяги от положения центра масс мобильного энергетического средства;

czi, Cz2 - приведённые жёсткости упругих элементов передней и задней подвесок мобильного энергетического средства;

«zi, «z2 - коэффициенты демпфирования в передней и задней подвесках мобильного энергетического средства и шин движителей;

V_cx - скорость МТ А.

Скорость МТА определяем с использованием положений теории М.В. Келдыша:

Рех

®₄ • г₀ • 1 - 8_Х • R₂ - £,---signet^

^0

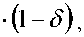
где Го - свободный радиус пневматического колеса;

£1, £2 - коэффициенты, учитывающие деформацию волокон шины от действия вертикальных и продольных сил;

д - коэффициент буксования движителя мобильного энергетического средства.

0, если Т < ф₀К

Буксование движителей мобильного энергетического средства в зависимости от толкающей силы Т(Х), реализуемой в контакте ведущего колеса с опорным основанием, можно представить в виде системы дифференциальных уравнений:

ln[k-A-T)/k-^₀)-A] К₆

0,9, если Т > ф R

если ф0К АТ < фК

где фо, ф - коэффициенты, характеризующие взаимодействие движителей мобильного энергетиче ского средства с опорным основанием.

Силу тягового сопротивления МТА Р_с можно представить в виде [2, 3]:

Л- = Го + Л/ЩҚ, -Го)]-(1 -/■'')+ Fit\ где Рсо - среднее значение тягового сопротивления при скорости движения МТ A Vo,

NP_C - скорость изменения тягового сопротивления при увеличении скорости движения агрегата с Vo до V_cx;

F(t) - случайная функция, характеризующая изменение тягового сопротивления агрегата по времени;

к_т - коэффициент, определяемый экспериментально.

При решении системы уравнений, описывающей движение МТА на базе мобильного энергетического средства с гидростатической трансмиссией, приведённой к каноническому виду, нами был принят метод Рунге-Кутта.

Результаты анализа экспериментальных и полученных при решении математической модели диаграмм разгона МТА показали, что относительная погрешность расчётов не превышает 6,5%, значения критериев Стьюдента и Фишера не превышают табличных значений, а коэффициент корреляции показывает тесную связь между сравниваемыми результатами.

Выводы. На основании вышеизложенного математическую модель МТА на базе мобильного энергетического средства с гидростатической трансмиссией можно считать вполне удовлетворительной. Следовательно, с помощью полученной математической модели можно провести теоретические исследования влияния неустано-вившегося характера тяговой нагрузки на выходные показатели работы МТА на базе мобильного энергетического средства с гидростатической трансмиссией.