Математическая модель материальных потоков в зерноуборочном комбайне

Введение. Для разработки эффективной системы адаптивного управления зерноуборочным комбайном необходимо контролировать параметры материальных потоков его рабочих органов. Математическая модель динамики материальных потоков позволит выявить влияние рабочих органов машины и режимов их работы на загрузку молотильно-сепарирующего устройства (МСУ), вымолот зерна и его сепарацию на различных участках технологического процесса, определить возможные способы снижения потерь зерна при уборке. В статье предлагается вариативнодекомпозиционный метод моделирования динамики материальных потоков в комбайне РСМ-181 Torum-740.

Постановка задачи исследований. Количественной характеристикой загрузки комбайна является подача хлебной массы q , а качественной — состояние подаваемой растительной массы ω: влажность и соломистость. В настоящее время нет апробированных технических средств для непосредственного измерения подачи и качественного состояния хлебной массы. Поэтому моделирование материальных потоков в зерноуборочном комбайне является перспективным направлением исследования интенсификации процессов обмолота и сепарации, а также построения адаптивных систем управления. Большинство существующих моделей материальных потоков в комбайне основаны на том, что количественные и качественные характеристики рассматриваются как постоянные величины. Кроме того, скорость движения v _к комбайна также задаётся постоянной. Однако в реальных условиях эти характеристики являются переменными, имеют статистическую природу и оказывают значительное воздействие на технологический процесс. Для построения математической модели материальных потоков необходимо представить функциональную схему технологического процесса и провести её декомпозицию на последовательные этапы преобразования хлебной массы.

Вариативно-декомпозиционный метод моделирования динамики. Отличительной особенностью этого метода является реализация переменных (вариативных) качественных и количественных характеристик технологического процесса, таких как соломистость, влажность и урожайность растительной массы, скорость движения комбайна и ширина рабочего захвата жатки. Декомпозиция технологического процесса на последовательные этапы преобразования хлебной массы позволяет моделировать динамику материальных потоков в каждом рабочем органе, выявлять влияние возмущающих воздействий и конструктивных параметров на режимы работы МСУ и потери зерна. Несмотря на различный принцип действия и конструктивное исполнение рабочих органов комбайна, все они преобразуют потоки материалов, поэтому для каждого из них справедливо уравнение материального баланса [1]:

dMldt = Qi - Q2, где M — содержание обрабатываемого материала в рабочем органе комбайна; Q1 , Q2 — потоки материала, подводимого и отводимого от рабочего органа.

Из уравнения видно, что при неустановившемся режиме подача хлебной массы уравновешивается отводимыми продуктами обработки и увеличением или уменьшением её содержания в рабочих органах комбайна. Количество материала, содержащееся в рабочих органах при установившемся режиме работы, характеризует их удерживающую способность. Чем больше эта способность, тем равномернее работает молотильно-сепарирующее устройство (МСУ) и тем меньше потери зерна.

Каждая из операций технологического процесса характеризуется содержанием зерна: необмолоченного Xi , свободного (идущего сходом) Yi и выделяемого через сепарирующую поверхность Zi (рис. 1). Для любого отрезка времени движения хлебной массы обеспечивается соотно- шение Xi + Yi + Zi = qi = const.

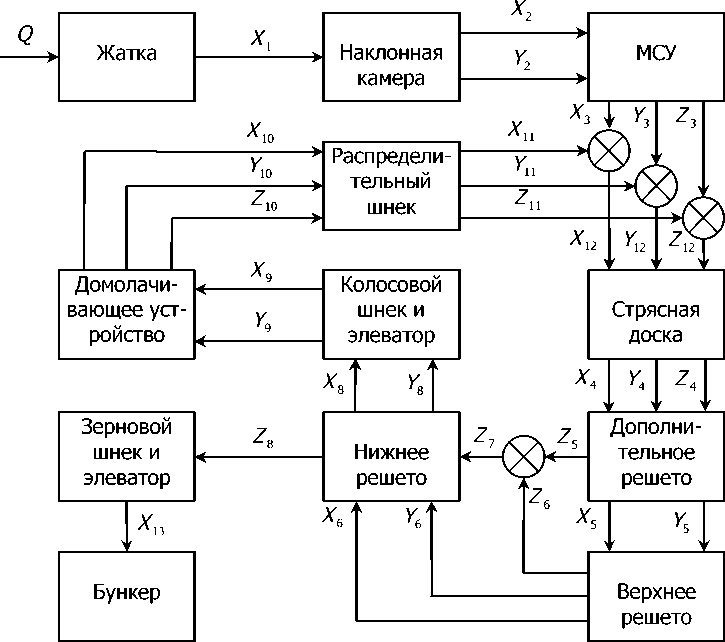
Рис. 1. Структурная схема технологического процесса

Количество материала, проходящего за единицу времени через i -е сечение потока в технологической схеме, принято за расход q i . Составляющие параметра q i описываются системой дифференциальных уравнений:

\ dXJA = - b i X i ;

\YYjdt = - b i X i - jY i ;

[ dZ i/ dt = jY i .

После решения этой системы уравнений, запишем

X i - Q . e b i t ;

Y =V ^b q i /{ j i - b ) ]- ( e - b i t - e ^- j i t ) ;

Z - [qiК ji - bi)] ■ [bi (e-jit - 1) (e-bit - 1)], где ji и bi — коэффициенты, характеризующие конструктивные параметры рассматриваемого i-го рабочего органа комбайна.

Зная зависимость коэффициентов j i и b i от качественных характеристик технологического процесса [2], запишем:

У _ у d ^- civi ^- aili .

X i ^- X i - i^e         ;

Y - Y ,e^- m i L i I         I - 1

+ X i i i -1

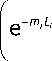
+ m e civi-miLi

a

^{- m}i

— a e ^- cv ^- aL

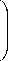
Z - Y 1 (1 - e ^{- m} i ^{L i} ) + X, , 1 - e ^{- m} i ^{L i} i i - 1                               i - 1

+

m e c i v i ^{- m} i L

- a e ^- cv ^- a i L i

a

- m_i

где c i — коэффициент, учитывающий обмолот хлебной массы за счёт первого удара рабочего органа; v i — скорость удара рабочего органа по массе; a i — коэффициент, характеризующий интенсивность обмолота хлебной массы в зоне действия рабочего органа; l i — длина зоны действия рабочего органа; m i — коэффициент сепарации; L i — длина сепарирующей поверхности. Коэффициенты m i , c i и a i зависят от физико-механических свойств обмолачиваемой массы, конструктивных и режимных параметров рабочих органов.

Математическая модель динамики потоков. Учитывая порционность tж, вносимую транспортирующими органами в подачу хлебной массы и вороха, уравнение жатки запишем в виде q- kq -aq (t- tx), в соответствии с которым получим передаточную функцию жатки: W ж (s) - KQe stж, где Kq, Жж — коэффициент передачи и запаздывание жатки.

Поток хлебной массы из жатки транспортируется битерами наклонной камеры в МСУ. Сделав допущение, что все битеры наклонной камеры действуют одинаково на поток материала и обмолачивают хлебную массу только за счёт единичного удара ( 1 2 - 0 ) , запишем

X2 - q1e-cv2 ]n, Y2 - [q1 (1 - e-c2v2)]n, где n — количество битеров в наклонной камере.

Из наклонной камеры поток хлебной массы перемещается в МСУ, где происходят обмолот материала ротором и сепарация сквозь решётчатую деку. Вместе с соломой сходит часть непросеянного и необмолоченного зерна. Изменение расходов отводимых продуктов из МСУ связано с изменением подачи q 2 , частоты вращения ротора ν p , конструктивных параметров и физикомеханических свойств ω обрабатываемой массы. Необмолоченная в МСУ хлебная масса подвергается повторному обмолоту в домолачивающем устройстве. Для МСУ ( i - 3 ) и домолачивающего устройства ( i - 10 ) преобразования материальных потоков запишем уравнениями:

У _ у d ^{- c}3^v з ^{- а}з¹ з ' Y — Y ^^{- c} 10 ^v 10 ^{- a} 10 l 10 •

X 3 ^- X 2 e ; X 10 ^- X 9 e          ;

Y 3 - Y 2 e ^{- m3}L³ + X 2 1 e ^{- m3}L³

m e - c ₃ v ₃ - m ₃ L ₃ + —----

-

a e ^c 3 ^v 3 ^- a L 3

^a 3 ^{- m} 3

;

Y ₁₀ - Y 9 e ^- m ¹⁰ L ¹⁰ + X 9 1 e ^- m ¹⁰ L ¹⁰

#77 p ^c 10 ^v 10 ^m 10 L 10

+ ^m10^e _________

a 10

-

a d ^c 10 ^v 10 ^a 10 L 10 10 e

-

m 10

;

Z 3 = Y 2 ( 1 — e ^{— m 3} L ³ ) + X 2 1 1 — e ^— m ³ L ³

m e ^— c 3 v 3 ^{— m} 3 L 3 + —----

—

a ₃e

— a 3 L 3

a ₃

—

m ₃

;

Z ₁₀ = Y 9 ( 1 — e m ¹⁰ L ¹⁰ ) + X 9 1 1 — e m ¹⁰ L ¹⁰

— c 10 v 10 — m 10 L 10

+ ^m 10 e _________

—

a о ^c 10 v 10 ^a 10 L 10

10 e

a 10

—

m 10

.

Суммарные потоки X12 = X3 + X11, Y12 = Y3 + Y11, Z12 = Z3 + Z11 вороха из-под МСУ и домо- лачивающего устройства стрясной доской транспортируются в систему очистки. Для стрясной доски уравнение потоков запишем в виде:

X 4 = X 12 e ^— c ⁴ v ⁴ , Y 4 = X 12 ( 1 — e ^— c ⁴ v ⁴ ) , Z 4 = Z 12 .

vlag

Sol

u

Y2

Наклонная

X2

X2

Y2

Урожайность

X12

МСУ

Bp

X9

Y12

1.2

Y9

X9

Скорость

Z12

X9 X8

Y9

X10

Y10

Z10

X3

Y3

Z3

Домолачивающее устройство

Y9 Y8

Распределительный шнек

X10X11 X1

Y10Y11     Y11

камера gr Потери МСУ Анализатор потерь МСУ

Влажность

Соломистость

X10

Y10

Z10

Колосовой

шнек и элеват ор

X8

Y8

Z8

X8

Y8

Z8

X6

Y6

Z7

in %

out gr

0.1

Масса зерна

Tb.s

Бу нкер

Зерновой шнек и элеватор

-C-

Объём бункера

% gr

Потери Анализатор очистки потерь очистки

X3

Y3

Z3

Дополнительное

Нижнее решето

Z7

X6

решето Z5

Y6

Стрясная доска

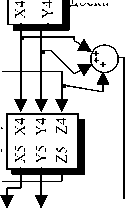
Верхнее р ешето

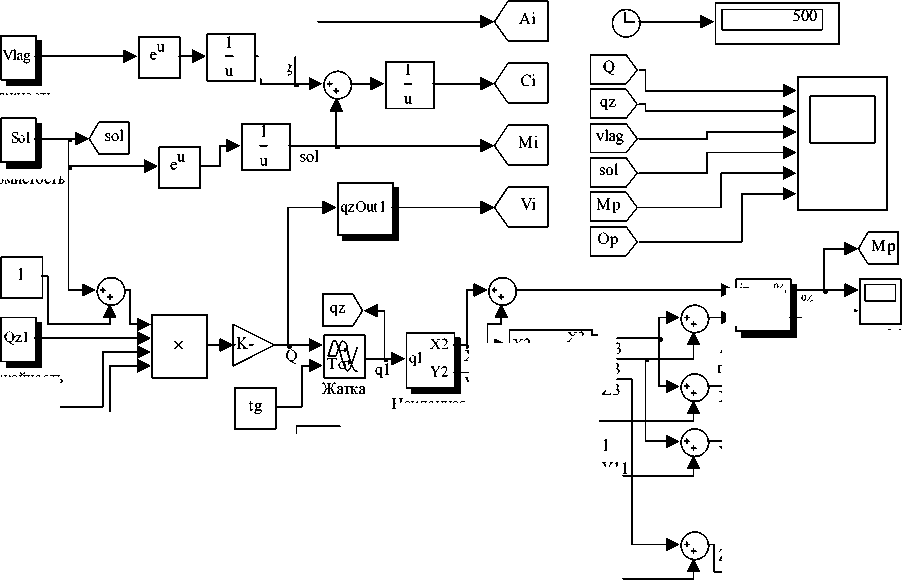
Рис. 2. Модель динамики материальных потоков в Matlab Simulink

В системе очистки происходит разделение массы на зерновой ( Z ₈ ) и незерновые ( X 8 и Y 8 )

потоки. Материальный поток (X8 + Y8) характеризует потери в системе очистки комбайна. Пре- небрегая малыми значениями коэффициентов с5,6,8 и v5,6,8, уравнения материального баланса системы очистки запишем в виде:

X 5 = X 6 = X 8 = X 4 , Z 7 = Z 5 + Z 6 ,

,

Y 5 = Y 4 e ^- m ⁵ L , Y ₆ = Y ₅e ^- m ⁶ L , Y 8 = Y ₆e ^- m ⁸ L , Z ₅ = Y 4 ( 1 - e ^- m ⁵ L ⁵ ) , Z ₆ = Y₅ ( 1 - e ^- m ⁶ L⁶ ) ,

= Y 5

m 5     ₍ e - m 5 L 5

- e - ^m 6 L ) . ( 1 - e - ^m 8 L 8

Z 8

m - m 65

Урожайность, ц/га 50

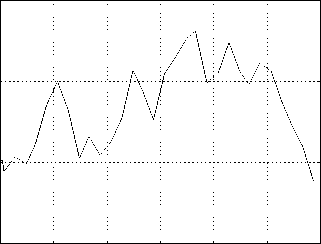
0   50 100 150 200 250 t , c

Подача растительной массы, кг/с 10

0   50 100 150 200 250 t , c

Соломистость хлебной массы

Потери зерна в МСУ, %

1.8

1.6

1.4

1.2

0   50 100 150 200 250 t , c

Влажность хлебной массы, %

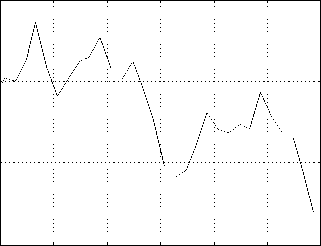
0   50 100 150 200 250 t , c

Потери зерна в системе очистки, %

1.6

1.4

1.2

0.8

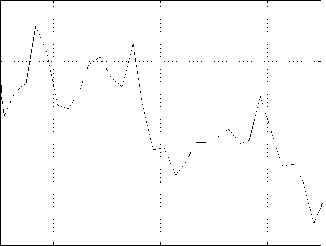
0   50 100 150 200 250 t , c

0   50 100 150 200 250 t , c

Рис. 3. Результаты моделирования

Хлебная масса перемещается от одного рабочего органа к другому с помощью шнеков и элеваторов. Полагая, что при перемещении свойства продуктов не изменяются, динамические свойства транспортирующих устройств можно выразить в операторной форме:

a = 7 e st ^{13 q} 13    Z 8 e

Y — Y о - st ii ■ X 11 = X 10 e ;

3 . у _ у -stst . у _y -s-^st9 .

; X 9     X 8 e    ; / 9    Y 8 e    ;

- st ii - st ii

; '11    '10e     ; ^11    ^10e , где t9 , t11 , t13 — время перемещения потока колосовым шнеком и элеватором от нижнего решета в домолачивающее устройство, распределительным шнеком из домолачивающего устройства на стрясную доску и зерновым шнеком и элеватором в бункер соответственно.

Накопительной ёмкостью комбайна является зерновой бункер, который описывается передаточной функцией бункера, устанавливающей динамическую зависимость между текущим количеством зерна в бункере и подачей:

W6 (s )=A,

Tбs где Тб — время наполнения бункера зерном.

Разработанный вариативно-декомпозиционный метод моделирования динамики материальных потоков комбайна реализован в системе Matlab Simulink (рис. 2). Разработанная математическая модель описывает совокупность основных операций, выполняемых комбайном РСМ-181 Torum-740.

Анализ результатов моделирования (рис. 3) показывает, что полнота обмолота и сепарации зерна в МСУ комбайна имеет итерационный характер и зависит как от физико-механических свойств хлебной массы или продуктов обмолота, так и от конструктивных и режимных параметров рассматриваемого элемента системы и ему предшествующих, каждый из которых изменял состояние материала.

Выводы. Разработанный вариативно-декомпозиционный метод моделирования динамики материальных потоков реализован в системе Matlab Simulink (рис. 2). Полученная математическая модель описывает совокупность основных операций, выполняемых комбайном РСМ-181 Torum-740. Анализ результатов моделирования (рис. 3) показывает, что полнота обмолота и сепарации зерна в МСУ комбайна имеет итерационный характер и зависит как от физико-механических свойств хлебной массы или продуктов обмолота, так и от конструктивных и режимных параметров рассматриваемого элемента системы и ему предшествующих, каждый из которых изменял состояние материала.