Математическая модель метаморфизма кристаллических структур в кубическую

Метаморфизм (преобразование) как явление наблюдается не только при трансформации горных пород, но и в широко известных и используемых изоморфизме и полиморфизме. Приемы метаморфизма используются в математике, например, при превращении нелинейной зависимости в линейную.

Из семи кристаллических сингоний наиболее удобной для расчетов является кубическая.

В работах автора [1-3] изложены и обоснованы адекватностью со справочными (рентгеноструктурными) данными математические модели расчетов ионных радиусов и фрагментов структурных составляющих сложных (многокомпонентных) веществ.

В основе разрабатываемой гипотезы лежит следующее.

• 1.    Для кристаллического вещества справедлива статистика Л. Больцмана (статистика в поле сил).

• 2.    Между частицами (атомы, ионы, ассоциации и т.д.) осуществляется электромагнитное взаимодействие (закон Ш. Кулона).

Чисто математически из межструктурных расстояний (а, Ь, с) и углов ( а , /3, у) для любой сингонии рассчитывается V - объем элементарной ячейки. W = d - межплоскостное расстояние в эффективной кубической сингонии.

В математической модели расчета эффективных ионных радиусов [3] используются две характеристики: а - структурная константа и r_D - дебаевский радиус экранирования в кристаллическом веществе. Эти константы наряду с характерной для кубической сингонии включают «память» об исходной, т.е. являются комбинациями специфических структурных величин. В кубической сингонии наиболее жесткая конструкция - тетраэдр, потому в r_D должен входить ⁼ 17,581767 [3] (ZnS - сфалерит). Объемная структурная постоянная, являющаяся произведением величин, меньших единицы, сама не превышает — = 0,57735.

В модели эффективных ионных радиусов критериями достоверности расчетов являются постоянства радиусов катионов г_к и минимальных радиусов анионов [3]. Радиусы катионов остаются постоянными в конденсированных средах [3, 6]. В нашем случае критерий - постоянство минимального радиуса аниона. Здесь и далее линейный размер выражается в ангстремах (10^-8 см).

Результаты расчетов и их обсуждение

В качестве исследуемых веществ используем карбонаты щелочно-земельных металлов (Са, Sr, Ba, Ra и Mg) (электронное строение ионов sf/f а так же Мп, Fe, Со, Ni (i/"'⁸), кристаллизующихся в орторомбической, ромбоэдрической и гексагональной сингониях. Так, карбонаты Са, Sr, Ba, Ra кристаллизуются в орторомбической сингонии, Mg, Са, Мп, Fe, Со, Ni - в ромбоэдрической и эти же вещества - в гексагональной.

Орторомбическая сингония (ОР. Р_тс„-4) [4, 5, 7, 8].

Характеристики: периоды кристаллической решетки а, Ь, с.

Объем элементарной ячейки F = a-b-c.

Эффективное межплоскостное расстояние куба d = 7^ = ^Jabc .

Эффективное межструктурное расстояние [3] r_p=ad.

Дебаевский радиус экранирования [3]

rD = 17,581767//2, где f и f_ - функции зарядности и структуры в соответствующих сингониях и кубической.

Минимальный радиус аниона г^ (Л - СО^) [3]

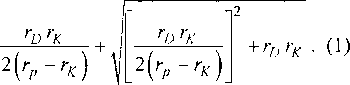
В табл. 1 приведены исходные (справочные) данные по параметрам решеток и результаты расчетов. В качестве примера рассмотрим СаСО3 (арагонит) с периодами решетки а = 6,959; 6 = 5,735; с = 4,951.

d = 75,959-5,735-4,951 = 7197,593742 =

= 5,82449 .

r_p -ad; а = а_ОР

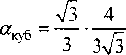
= 0,44444... .

^rD - ^rD(ZnS) ’ /(ЭР ' /куб -

= 17,581767 ■ 4(7з -1) ■ — = 63,053 524 .

'         ' 2

г_п = —-5,82449 = 2,58866, г ₂₊ = 1,01202.

Р 9                            Са² ’

₀   ___ 63,053 524-1,01202

Гсо32' ~ 2(2,58866-1,01202) +7409,516253 + 63,811427 = = -20,236508 + 21,75609 = 1,51959.

Таблица 1

Карбонаты орторомбической сингонии (Pmcn~4)

Вещество	а	ь	с	V	d	гр	7О2-
СаСО3 (арагонит)	6,959	5,735	4,951	197,59374	5,82449	2,58866	1,51959
SrCO3	4,505	8,417	6,092	231,00002	6,13579	2,72702	1,51959
ВаСО3 (витерит)	6,390	8,581	5,200	285,12947	6,58184	2,92526	1,51958
RaCO3	-	-	-	290,53187	6,62315	2,94362	*

* Расчет по т° _г_ = 1,51959.

По аналогичной схеме рассчитан r^- из данных для SrCO₃ и ВаСО₃. Для RaCO₃ в литературе [7] приводится только энтальпия образования. Из аналогии свойств проведен расчет r_p , d и V для этого соединения. Из данных табл. 1 следует хорошее согласие в величинах г^- •

Ромбоэдрическая сингония (РЭ, R3c-2).

Характеристики: а, а .

V = a3 f^a°Y где /(«”) = д/1 - 3cos2 а + 2 cos3 а .

д=^/х«5-

Катионы с электронным строением s2p6

r_p-ad; а = а_па^ = ^7з^-1)'~ =0,517638.

r_D ^(ZnS) -/рэ - /куб =17,5 81767-276 =

= 86,132725 .

Справочные данные и результаты расчетов приведены в табл. 2. Рассмотрим в качестве иллюстрации СаСО₃ (кальцит) с характеристиками решетки а = 6,3758; а = 46°6'.

/(«“) = 0,473588.

d = ^6.3758³ -0,473588 = ^/122,806410 = 4,97058.

r_p=ad =2,57296.

„    _    86,132725-1,01202

W ~ 2(2,57296-1,01202) + +7761,209086 + 87,168040 =

= -27,921650 + 29,441239 = 1,51959.

Катионы с электронным строением d5 "8

Дебаевский радиус экранирования катионов с незавершенной Доболочкой отличается от rD ка тионов с завершенными оболочками. В нашем случае

о rD =

= 54,137777.

/ х V2

а = а_РЭ - «куб = (73 -1)- — = 0,517638 .

Рассмотрим FeCO₃ (сидерит): а = 5,7657; а°=47°25'; /(а°) = 0,496018.

Д = ^5,7657³-0,496018 = 795,07220 = 4,56406. r_p=ad =0,517638-4,56406 = 2,36253.

₀    _   54,137777-0,75152

“ 2(2,36253-0,75152) +7159,450344 + 40,685622 =

= -12,627365 + 14,146942 = 1,51958.

Таблица 2

Карбонаты ромбоэдрической сингонии (R3c-2 )

Вещество	а	а		V	d	гр	^02-
MgCO3	5,5967	48°12'	0,509350	87,39109	4,43766	2,29711	1,51958
СаСО3 (кальцит)	6,3758	46°06'	0,473588	122,80641	4,97058	2,57296	1,51959
МпСОз	5,852	47=45'	0,501690	99,89734	4,64058	2,40214	1,51958
FeCO3 (сидерит)	5,7657	47°25'	0,496018	95,07220	4,56406	2,36253	1,51958
СоСОз	6,668	48=14'	0,509918	92,87168	4,52857	2,34416	1,51959
№СО3	-	—	—	89,43156	4,47195	2,31485	*

* Расчет по среднему г^. = 1,51958.

Рябухин А.Г.

Таблица 3

Карбонаты гексагональной сингонии (ЯЗс-6 )

Вещество	а	с	с?с	V	d	гр	'со/
MgCO3	4,529	14,843	304,45726	263,66772	6,41238	2,32697	1,51962
СаСО3	4,990	17,031	421,52413	365,05061	7,14690	2,59352	1,51956
МпСО3	4,905	15,932	383,30839	331,95480	6,92404	2,37596	1,51957
FeCO3	4,917	15,041	363,64459	314,92545	6,80356	2,33461	1,51956
СоСОз	4,861	15,012	354,72337	307,19945	6,74746	2,31536	1,51958
NiCO3	-	-	-	295,05836	6,65737	2,28445	*

* Расчет по среднему г^. = 1,5195 8+0,00004.

Справочные данные и результаты расчетов помещены в табл. 2. Рассчитанные значения г^. хорошо согласуются между собой. Для NiCO₃ отсутствуют сведения о параметрах решетки. В табл. 2 приведены величины г_р, d и Р_М;_СОз , рассчитанные по изложенной методике с использованием г_№2₊ = 0,69603 и среднего г^. = 1,51959.

Гексагональная сингония (Г, R3 с - 6).

Характеристики: периоды кристаллической решетки а и с.

7з 2

Объем элементарной ячейки V = — а с.

Катионы с электронным строением s2p6

Результаты расчетов и справочные данные приведены в табл. 3. Рассмотрим СаСО₃: а = 4,980; с = 16,9967.

У = — 4,980² 16,9967 =365,051321.

/ = ^ = 7365,051321 =7,14690.

| о /9

« = «г-«куб=з-^~ = 0,362887.

^rD⁼ ^D(ZnS) ' /г '/^=17,581767-4(72 -1)-4 =

= 58,260850.

г_р = ad =0,362887-7,14690 = 2,59352.

°    -    58,26085-1,01202

~~ 2(2,59352 -1,01202) +

+7347,482902 + 58,961145 =

= -18,640893 + 20,160458= 1,51956.

Полученная величина хорошо согласуется с полученными ранее.

Катионы с электронным строением d5 "8

72 -1

а = а_Т ■ а- = -7=--2 = 0,343146 .

72 + 1

r_D = ^(ZnS) /г ■ /куб = 17,581767 - 472 - ^ = = 76,562413 .

Рассмотрим, как прежде РеСО₃: а = 4,917; с — 15,041.

Р = ™4,9172-15,041 =314,925450.

/ = 7Й = 7314,925450 =6,80356.

г_р = ad = 0,343146-6,80356 = 2,334461.

_о _   76,563413-0,75152

~ 2(2,33461 - 0,75152) + +7330,248698 + 57,538185 =

= -18,172746+ 19,692305 = 1,51956.

Таким образом, и в этом случае величина г^- согласуется с полученными ранее.

Заключение

• 1.    На примерах орторомбической, ромбоэдрической и гексагональной сингоний показана возможность метаморфизма сложных кристаллических структур в псевдокубическую.

• 2.    Показана возможность расчета минимального радиуса сложного аниона из структурных характеристик различных сингоний. Эффективный минимальный радиус в кристаллах

  г^ = 1,51959+0,00003 А.

• 3.    Показано, что в дебаевский радиус экранирования двухзарядных катионов во всех случаях входит тетраэдрический сомножитель

  Г_№)= 17,581767.

• 4.    Показано, что дебаевский радиус экранирования различен для s²p⁶ и /'-катионов.

• 5.    В псевдокубической решетке сохраняется «память» о прежней структуре, проявляющаяся количественно в величинах межчастичных расстояниях г_р .