Математическая модель морских течений и цунами

Морские течения, водные и песчаные цунами можно представить в виде ограниченной или замкнутой полосы, движущейся с постоянной скоростью и при этом сохраняющей форму сечения на всем своем протяжении. Эти явления поражают своей грандиозностью, организованностью и демонстрацией существования в своем объеме неиссякаемого источника колоссальной энергии. Какова внутренняя структура такой полосы и как устроен ее двигатель? Зная ответы на эти вопросы, можно далее строить предположения о причине возникновения таких явлений. Но прежде всего нужно найти ответы на первые вопросы, что в

Доклады независимых авторов 2024 выпуск 62 принципе можно попытаться сделать и не зная условий их возникновения.

Прежде всего появляется желание отождествить такие явления с электромагнитной волной – тоже бесконечной, сохраняющей форму, движущейся и переносящей энергию. Но в вакууме такая волна не тратит энергию на пути своего распространения и, следовательно, не нуждается во внутреннем источнике энергии. В потоке жидкости всегда есть внутренние потери и поэтому такой источник необходим. Мы сразу же начнем с утверждения, что движущими силами в рассматриваемых явлениях являются силы Кориолиса. Весьма живучим является мнение о фиктивности этих сил. Однако недавно появилось математически обоснованное доказательство физического существования этих сил [1, 2] и примеры конструкций [3], существование которых необъяснимо в отсутствии физических сил Кориолиса.

Автор уже рассматривал математические модели течений и цунами на основе уравнений гравитомагнетизма [4]. Ниже предлагается другая модель, основанная на использовании сил Кориолиса. Возможно, что эти модели удастся объединить, но здесь не делается таких попыток и не выполняется какое-либо сопоставление прежней и новой моделей.

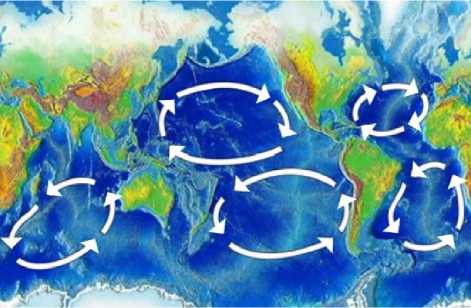
Рис. 1. Пять основных океанических циклов

Принятые представления о причинах океанских течений плохо согласуются с существованием замкнутых траекторий течения и устойчивостью конфигурации и формы сечения. Обычно выделяют градиентные течения, течения, вызванные ветром, приливные течения. Эти факторы могут служить причиной возникновения течений, но не могут поддерживать существование (в течении столетий) замкнутой траекториии течения (поскольку противоположно направленные участки этой тректории должны подвергаться противоположно направленным воздействиям). Однако течения, как правило, являются замкнутыми (как можно видеть на рис. 1 из [5]). Также для объяснения этих явлений обычно указывают на отличия в составе и свойствах вод струи и окружающих вод. Естественнее (на наш взгляд) предположить, что эти отличия являются следствием обособленности струи, а не причиной этой обособленности.

Для объяснения причин существования цунами обычно указывают на первоначальный толчок от землетрясения, а для прогноза поведения цунами (что чрезвычайно важно для практики) используется статистика прошлых цунами и карты морского дна. Этим занимаются десятки институтов и сотни ученых [6]. Но нас здесь интересуют общие закономерности движения цунами . Посмотрим на рис 2 из [4]. Кажется неубедительным представление о первоначальном толчке, как о причине длительного движения этой махины. Создается впечатление, что внутри этого "устройства" есть собственный двигатель, а сопротивление среды – лишь катализатор, сила, которая давит на педаль газа.

Итак, должны существовать внутренние силы, обеспечивающие движение, устойчивость конфигурации и формы сечения указанных потоков.

2.    Уравнения гидродинамики для прямоугольной волны

Для описания струи следует использовать гидродинамику. Уравнения гидродинамики для вязкой несжимаемой жидкости имеют следующий вид [7]:

div(v) = 0,                                       (1)

P^t + ^P - ^Av + ^ (v ’ ^)v - PP = 0,         (2)

где p = const - постоянная плотность,

^ - коэффициент внутреннего трения, р - неизвестное давление, v = \vx, Vy, vz] - неизвестная скорость, вектор,

Р = \p x , P y , P_z\ - известная массовая сила, вектор,

• X, y,Z,t - пространственные координаты и время.

В этих уравнениях неизвестны р, V .

Рис. 2.

Если система является замкнутой, то система уравнений (1, 2) в стационарном режиме принимает вид [7]:

div(v) = 0,                                          (3)

• -p- 6v + VD - p - F = 0,                     (4)

где неизвестны D, V. Уравнение (4) решается методом, предложенным [7]. При этом решение всегда существует и является единственным. После решения уравнения (4) определяются скорости и величина D, а давление вычисляется по уравнению вида p = --(W2) (кгм-^сек-2),                      (5)

где

W² = (v X + v² + v²).                          (6)

В (5) слева – давление, а справа плотность кинетической энергии течения . Интеграл плотности по объему определяет энергию в объеме струи (кг·м²·c^-2=джоуль).

Если система абсолютно замкнута (например, в безбрежном океане или просто при достаточно большом максимальном радиусе), то выполняется условие ^D ~ 0. Таким образом, для замкнутой системы выполняются уравнение вида р ■ Av + p ■ F = 0. (7) и определяется плотность энергии (5). Метод расчета таков, что не требует знания граничных условий – точность расчета тем больше, чем больше область интегрирования. В сущности, границы области существования течения определяются данными массовыми силами.

В нашем случае силы Кориолиса неизвестны, т.к. зависят от скоростей. Поэтому приходится выполнять расчет в каком-нибудь дополнительном предположения. Мы будем предполагать, что границы струи (ее радиус) известны и продольная скорость на границе струи известна.

Будем рассматривать математическую модель водоворота в системе прямоугольных координат г, ф, z . В уравнении (3.7) лагранжиан Av в прямоугольных координатах определяется формулой вида

Г ^ ^v x] A v = A V y =

I ^{A v} z\

у ¹ Ух , д²у _х д ²у_х дх² + ду² + дz²

а2

Ух1

^д2уУ₊^д2у У ₊ ^д2у У ^дх^{2     д}у^{2     д}г²

d²v _z . d²v _z . d²v _z - дх²    ду² дг² -

.

Массовые силы Кориолиса, создаваемые вращением Земли с угловой скоростью ш_о , определим как

^F x    ^2p^ o ^v z ,                                      ⁽ 9)

^F z    ^2p^ o ^v x ^{.                                      (10)}

Для средних широт ш_о ~ 10 " ⁵. Массовую силу тяжести определим как

^F y = -зр.

Запишем уравнение (7) с учетом (8-11): г 2^ _o ^v zl р■Av + pI -д 1 = 0.

²^ o ^VX^

При этом наша задача принимает вид системы трех уравнений с тремя неизвестными v_x, V_y, V_z :

р ■ Avx + 2pvzMo = 0, р ■ Avy - pg = 0, р ■ Avz + 2pvxwo = 0.

Далее будем искать решение в следующем виде:

V x = bxex ,	(16)
V y = by ,	(17)
vz = bzex,	(18)
где b, a, 0,/ — некоторые константы и ex = exp(^x + ay + /z) .	(19)
Подставляя (16-18) в (8), после дифференцирования получаем:
Г AVxl p2b x ex+a2b x ex+b x X2exl \ A v y \ = \b y                            1 A u z\   [^2bzex+a2bzex+bz/2ex]
	(20)
или Г Av~]   Fbr ex] 1 L Av zJ    PzexJ Подставляя .(16-17, 21) в (13-15), получаем bxex + 2qbzexM0 = 0	(21)
	(22)
b y - qg = 0	(23)
bzex + 2qbxsiw0 = 0	(24)
где q = - . M	(25)
Одним из решений системы уравнений (22, 24) может быть:
b x = b z ,	(26)
b x = 2q^ o ,	(27)
Из (23) получаем: b y = qg .	(28)
Из (9, 10, 16, 18, 26_28) получаем: vx = vy = 2qMoex ,	(29)
F X = fz=(2pw0)2ex,	(30)
Определим еще плотности потоков энергии, циркулирующих
в прямоугольной струе вдоль осей координат: S x = P x V x , S z = F z V z .	(31)
Из (29-31) получаем: S x = S z = (2p^ 0 ) 3 ex 2 .	(32)

Таким образом, мы определили аналитическое описание струи с прямоугольным сечением. Конкретные значения всех параметром можно будет определить при известной статистике измерений таких струй (океанских течений и цунами). У автора нет такой информации и он был бы рад сотрудничеству в любой форме.

Заметим, что при / > 0 величина экспоненты увеличивается при увеличении Z. Отсюда и из (32) следует, что поток энергии увеличивается по мере движения струи . Это является следствием работы сил Кориолиса, которые постоянно добавляют энергию в струю. Именно поэтому морские течения не затухают, а цунами ускоряются и расширяются.

Наконец, найдем давление внутри струи по (5, 6):

P = -^(vl + bj+vZ ) ex2.                      (33)

Это давление превращает струю в почти твердое тело и удерживает жидкость в объеме струи.