Математическая модель надёжности аппаратно-программных комплексов обработки информации для систем управления реального времени

Введение. Одной из главных характеристик аппаратно-программных систем обработки информации реального времени является надёжность [1-3].

Под надёжностью программного обеспечения (далее также - ПО) понимается свойство этого обеспечения выполнять заданные функции, сохраняя свои характеристики в установленных пределах при определённых условиях эксплуатации.

Надёжность ПО определяется его безотказностью и восстанавливаемостью. Безотказность ПО - это свойство сохранять работоспособность при использовании его для обработки информации в информационной системе (ИС). Безотказностью программного обеспечения оценивается вероятность его работы без отказов при определённых условиях внешней среды в течение заданного периода наблюдения.

Разработка систем реального времени требует большого количества ресурсов на проектирование и тестирование. Одно из решений данной проблемы является математическое моделирование аппаратно-программных комплексов. Это позволяет более гибко проектировать системы реального времени с заданной надёжностью с учётом ограничений по цене и времени разработки, а также открывается возможность более гибкой оптимизации аппаратно-программных комплексов систем управления реального времени.

Подобные модели с развитием вычислительных мощностей, эволюционных алгоритмов и нейронных сетей обретают всё большую актуальность.

Для разработки математической модели надёжности аппаратно-программного комплекса систем реального времени необходимо учитывать обеспечение заданного уровня надёжности при целесообразных затратах на разработку

Надёжность программного обеспечения. Надёжность архитектуры программного обеспечения включает как надёжность центрального ядра системы, так и надёжность индивидуальных компонентов, предоставляемых пользователю. Сбой отдельного компонента может привести к неработоспособности этого и, возможно, других компонентов ПО. Однако, это не должно приводить к неработоспособности всей системы в целом. Тщательный анализ программной архитектуры позволяет выявить компоненты, ошибки в которых оказывают наиболее существенное влияние на надёжность системы. Как правило, это компоненты, наиболее часто используемые или архитектурно связанные с множеством других компонентов. Существует много методов повышения надёжности программного обеспечения [4-5], но в настоящее время только подход мультиверсионного отказоустойчивого программирования является возможной альтернативой методам тестирования и верификации программ, обеспечивая высокий уровень надёжности функционирования критичного программного обеспечения [6]. При этом важно понимать, что верификация не гарантирует корректности, так как сами спецификации и/или системы верификации (как и любое другое ПО) могут содержать ошибки.

Использование систем поддержки принятия решений при мультиверсионном программировании позволяет уделять основное внимание качеству требований на этапе формирования надёжного ПО. Однако улучшение характеристик надёжности ПО с использованием избыточности требует дополнительных временных и финансовых ресурсов.

Поэтому основной вопрос на этом этапе заключается в том, каким образом, используя избыточность в архитектуре ПО, максимизировать надёжность и снизить стоимость разработки. Данная область включает в себя методы многокритериального принятия решений, ориентирующиеся на задачи с дискретным пространством решений. К настоящему времени разработано множество методологий многокритериальной поддержки принятия решений, учитывающих различные уровни информации о предпочтениях эксперта. Использование различных методов определения глубины мультиверсионности и многокритериального принятия решений при выборе архитектуры позволяет спроектировать программную систему, отвечающую предъявляемым требованиям.

В зависимости от количества и величины компонентов условные и безусловные вероятности сбоя, доступа, анализа и времени восстановления, а также и времени использования компонентов различны. Модель [7], приведенная ниже, может использоваться, чтобы оценить надёжность программного обеспечения для возможных архитектурных изменений, выбрать надёжную архитектуру из различных вариантов и имеет следующие обозначения:

• 1)    М - число архитектурных уровней в архитектуре ПО;

• 2) N j - число компонентов на уровне j , j е {1,.., M};

• 3) D ij - множество индексов компонентов, зависящих от компонента i на уровне j ,

i е {1,.., N j }, j е {1,.., M };

• 4)   F ij - событие сбоя, произошедшего в компоненте i на уровне j , i е {1,.., N j }, j е {1,.., M};

• 5)   PU ij - вероятность использования компонента i на уровне j , i е {1,.., N j }, j е {1,.., M};

• 6)   PF ij - вероятность появления сбоя в компоненте i на уровне j , i е {1,.., N j }, j е {1,.., M};

• 7) PL inm - условная вероятность появления сбоя в компоненте m на уровне n при

появлении сбоя в компоненте i на уровне j , i е {1,.., N j }, j е {1,.., M} , n е {1,.., N m }, m е {1,.., M };

• 8)    TA ij - относительное время доступа к компоненту i на уровне j , i е {1,.., N j }, j е {1,.., M}, определяемое как отношение среднего времени доступа к компоненту i на уровне j к числу сбойных компонентов на малых уровнях архитектуры за одно и то же время;

• 9)    TC ij - относительное время анализа сбоя в компоненте i на уровне j , i е {1,.., N j }, j е {1,.., M}, определяемое как отношение среднего времени анализа сбоя в компоненте i на уровне j , i е {1,.., N }, j е {1,.., M}, к числу сбойных компонентов на всех уровнях архитектуры, анализируемых в одно и то же время;

• 10)    TE ij - относительное время устранения сбоя в компоненте i на уровне j , i е {1,.., N j }, j е {1,.., M}, определяемое как отношение среднего времени восстановления в компоненте i на уровне j , i е {1,.., N }, j е {1,.., M}, к числу сбойных компонентов на всех уровнях архитектуры, в которых происходит устранение сбоев в одно и тоже время;

• 11)    TU ij - относительное время использования компонента i на уровне j , i е {1,.., N j }, j е {1,.., M}, определяемое как отношение среднего времени использования компонента i на уровне j , i е {1,.., N }, j е {1,.., M}, к числу компонентов на всех уровнях архитектуры, используемых в одно и то же время;

• 12)    TR - среднее время простоя системы в большой архитектуре ПО реального времени, определяемое как время, в течение которого система не может выполнять свои функции;

• 13)    MTTF (Mean Time to Failure) - среднее время появления сбоя в большой архитектуре ПО реального времени, определяемое как время, в течение которого сбоев в системе не происходит.

В архитектуре реального ПО среднее время появление сбоя, то есть время, в течение которого программное обеспечение функционирует корректно, равно [7]:

j = M i ' = N j                                       m = M     n = N m

[(1 - РЦ . ) x [TU. „ + S [(1 - PL” ) x TU m ]]] + S [(1 - PL )

IGDnm                                    kGDij m=M     n= Nm                         __

x [TU k, +    S    S [(1 - « km ) x [TU .m + S [(1 - PL; ) X TU m ]]]]]]}

( m = 1)&( m * j )    n = 1                                  I g D .m

Среднее время простоя (восстановления) программного обеспечения равно [7]:

j = M 1 ' = M j                                                   m = M     n = N n

[ PL . x [( TA m + TC„ + TE nm ) + S [ PL nmm x (TA m + TC m + TE m )]]]

I G Dnm

+ S [PLnm x (TAm + TCm + TEm)]]]]]]} l G Dnm

Среднее время простоя системы и среднее время сбоя могут быть использованы для предсказания надёжности программного обеспечения в целом. Для случая непрерывной эксплуатации сложного программного обеспечения (а для системы реального времени именно такой режим эксплуатации программного обеспечения является наиболее вероятным) надёжность программного обеспечения можно оценить с помощью коэффициента готовности S , вычисляемого по следующей формуле:

MTTF

= MTTF + TR "

Коэффициент готовности можно интерпретировать как вероятность корректного функционирования ПО.

Основной подход к увеличению надёжности программного обеспечения, к которому предъявляются повышенные требования по непрерывности и корректности функционирования, - мультиверсионная разработка, то есть создание независимыми друг от друга разработчиками нескольких версий компонента программного обеспечения, соответствующих одним и тем же спецификациям, но отличающихся реализациями. В архитектуре программного обеспечения должен быть предусмотрен механизм формирования общего результата работы данного программного компонента на основе результатов работы каждой отдельной версии. В [8] приводятся два основных метода построения архитектуры при использовании мультиверсионной разработки, которые сокращённо называются NVP и RB. При построении мультиверсионного компонента из K версий методом мультиверсионного программирования (NVP, N-version programming) для любого K надёжность равна:

R.. = pv ij ij

Кк

1 - П (1 - pk) k g Zu k        У7

где p^v ij – вероятность сбоя алгоритма голосования для компонента i на уровне j , Z ij – множество версий этого компонента, а p kij - вероятность сбоя версии k е Z j .

При построении мультиверсионного компонента из K версий методом блока восстановления ( RB , recovery block) надёжность равна :

R.. = K  p^k.pAT^k П 1 ^f (1 - p^l. ) pAT + pl (1 - pAT ) ) ,

¹j   _k e Z ^{4 4} l = Г j j      4 iJ 7

ij где pATij – вероятность безотказной работы приемочного теста для компонента i на уровне j, pkij - вероятность сбоя версии keZ,j.

Две последние формулы могут быть использованы для вычисления вероятностей отказов компонентов программного обеспечения:

PF.. = 1 - R... ij          ij

Надёжность аппаратного обеспечения. Для повышения надёжности аппаратной части комплекса также необходимо использовать избыточность и резервирование, что включает в себя мультипроцессорность и обеспечения разных шин и независимой оперативной памяти.

Каждый процессор и шина выходят из строя в некоторые случайные моменты времени, после чего начинается их восстановление. Будем предполагать, что потоки отказов и восстановлений являются простейшими. Интенсивность отказов шин обозначим как ν0, интенсивность потока восстановления шин - цо.  Интенсивность потоков отказов процессоров обозначим vi, а интенсивность восстановления процессоров i-го типа - цi.

Вероятность P jo,ji,_,jN нахождения системы в состоянии, в котором j о шин интерфейса исправны и участвуют в вычислительном процессе, а ( m 0 – j 0 ) неисправны и восстанавливаются, j 1 процессоров 1-го типа исправны и участвуют в вычислительном процессе, а ( m 1 – j 1 ) неисправны и восстанавливаются, ..., j N процессоров N -го типа исправны и участвуют в вычислительном процессе, а ( m N – j N ) неисправны и восстанавливаются, определяется по следующей формуле [9-10]:

P

N

-k^- П n j ! =⁰

= 0

m!

( mi ^{- j} i ) !

ρ j

,j_N⁼         _k! N

^ N M jо,-,Jn П j! = 0

i= 0

m!

( m i ^{- j} i ) !

, ρ j

N где ^k = ^ m i ,

а суммирование в знаменателе ведётся по всем возможным значениям индексов j0,…,jN (это же будет подразумеваться во всех последующих аналогичных формулах). Кроме того, используется следующее обозначение:

P i =

νi

μ i ^.

Формула для вероятностей состояний в стационарном режиме может быть несколько упрощена. Во-первых, мы можем сократить k ! в числителе и знаменателе, а также объединить произведения в числителе и знаменателе:

P

N

П i=0

m!

j⁼        N

N in j 0»“-» JN =0

(    -\Fpj

( mi - Jj F

m!

,

P

( mi - Ji ) W

Теперь перепишем знаменатель так, чтобы сначала выполнялось суммирование, а потом – вычисление произведения:

N

п

P           -    i= 0 '

j o Ji-* ,^j n    *m+

m!

j

(    '\FP i

( m i ^- Ji ) j!

m!

i- oj^ 0 ( mi- Ji) UJ

^, p j

Каждая из сумм в знаменателе теперь представляет собой произведение биномиального коэффициента и соответствующей степени фиксированной величины, и поэтому может быть упрощена с использованием формулы бинома Ньютона следующим образом [11]:

^mim!       j

17---- FF", Pi*

i= - 0 ( mi- Ji ) j!

m!

J- 0 ( mi^- J i ) Ui !

p J - 1 mi — ^j i

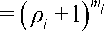
Таким образом, окончательно получаем следующее выражение для вероятностей состояний аппаратного обеспечения в установившемся режиме:

P

^J 0 ’ ^JV^е

, jN

N п г - 0

( m i

m!

^- Л ) -Ь!

■PJii

N

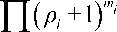
i - 0

Упрощённые формулы содержат меньше величин, чем исходные, и, следовательно, позволяют избежать выполнения некоторых ненужных операций (например, умножения и числителя, и знаменателя на к !, что, очевидно, не оказывает влияние на значение выражения) и требуют выполнения существенно меньшего количества операций для вычисления значения знаменателя, чем исходные формулы, приведённые в работах [9-10].

Зная минимальную конфигурацию аппаратного обеспечения, необходимую для выработки программным обеспечением системы реального времени управляющего воздействия в рамках требуемых заказчиком интервалов, можно вычислить надёжность аппаратной части. Действительно, если количество безотказно функционирующих шин оперативной памяти и процессоров превышает минимально требуемое, то «излишние» компоненты программного обеспечения можно рассматривать как резерв. Тогда надёжность аппаратного обеспечения системы управления реального времени, понимаемая как вероятность обеспечения минимальной требуемой производительности аппаратного обеспечения , может быть вычислена как сумма вероятностей нахождения аппаратного обеспечения в состояниях, в которых количество безотказно функционирующих шин оперативной памяти и процессоров превышает минимальное требуемое количество:

G cp

^J-^jx ^n’

₀   j ₀ m ₀

MN ^ jN ^ mN где M0 – минимальное требуемое для обеспечения заданной производительности число исправных шин памяти, Mi – минимальное требуемое для обеспечения заданной производительности число исправных процессоров i-го типа.

Формула для G cp подразумевает вычисление вероятностей различных состояний аппаратного обеспечения с различными значениями индексов j 0 , j 1 , … j N . При этом не целесообразнее повторять вычисления, которые уже были выполнены. Например, знаменатель всех формул имеет одно и то же значение, а, следовательно, его достаточно вычислить один раз.

Кроме того, так как требуется вычисление состояний с последовательными значениями индексов, то можно воспользоваться следующими рекуррентными формулами для степеней и биномиальных коэффициентов, следующих из определений степени и факториала:

• j. + 1 j.

Pi1 = Pi* • Pi’ mJ            mJ    m — j.

i              i      ii

( ^m * ^- j ^- 1 ) ^! ( j * ⁺ 1 ) !   ( ^m * ^- j ) UJ  Ji + ^{1 .}

Данные соотношения позволяют вычислять вероятности для состояний с последовательными значениями индексов с минимальным количеством дополнительных операций:

P.             =  =P. ,    , • mP .

j o ’ • -J i ^{+ 1} ’• “ ’Jn      jo’ • 'J i ’"' ’Jn   J. + 1

Из этого соотношения элементарными преобразованиями можно получить и формулы «уменьшения индекса»:

P.      .      .  = P.      .  ₁        • .  ^{Ji + 1}   ’

^J 0’" • - Ji ^¹ jJn    ^J0T • -Л⁺¹ ’ ^ ’^J N  ( m_f — J ) P

P.   . .   . = P.   .   . • -—^Ji—— .

Jo,-• -J—  ¹ v- > ^jn     Jos’• • -Ji’^ j Jn  ( m _; — J + 1 ) p

Так как наиболее простой вид формулы для вероятностей состояний принимают в случаях, когда все шины и процессоры исправны, либо когда все они не исправны, то вычисления G cp целесообразно начинать с вероятности состояния, в котором все шины оперативной памяти и процессоры исправны:

p

Pm o , m i ’ — ’m N

N

П Pm i=0

N ,

П( Pi+1) m i=0

а затем, используя формулы «уменьшения индексов», последовательно вычислить остальные необходимые вероятности состояний.

Ещё одна возможность для улучшения открывается, если минимальная конфигурация, обеспечивающая заданную производительность, включает меньше аппаратных компонент, чем половина компонент, присутствующих в системе. В этом случае можно вычислить сумму вероятностей состояний, в которых производительность не достаточна для выработки управляющего воздействия в рамках заданных временных ограничений, а затем вычислить требуемую вероятность как вероятность противоположного события [12]:

G cp = ¹ -     ^     ^Pi i i ,

0 < j < M     ^{Jo J}"" ^,J N

0 <  J n <  M n

При вычислении по этой формуле следует начать с вероятности состояния, в котором все шины оперативной памяти и процессоры неисправны:

р =-----1-----

0,0,...,0        N                      ’

П( Pi+1) mi i=0

а затем использовать формулы увеличения индексов, полученные выше.

Модель надёжности аппаратно-программного комплекса. Наконец, мы можем, используя приведённые выше соображения, объединить модели надёжности программного обеспечения и аппаратного обеспечения в общую модель надёжности многопроцессорного аппаратно-программного комплекса системы управления реального времени с мультиверсионным программным обеспечением.

В силу абстрактного характера программного обеспечения и пренебрежимо малой вероятности ошибок при его копировании и распространении (кроме того, целостность программного обеспечения может быть проконтролирована с помощью таких механизмов как контрольные суммы), можно считать, что отказы аппаратной и программной части происходят независимо.

Поэтому вероятность одновременной безотказной работы аппаратно -программного комплекса равна произведению вероятностей безотказной работы программной и аппаратной частей [12]:

P F =G cp • S .

Заключение. Таким образом, мы получили модель расчета надёжности многопроцессорных аппаратно -программных комплексов систем реального времени с разнородными процессорами и мультиверсионным программным обеспечением, используя теорию массового обслуживания и теорию надёжности, которая позволяет рассматривать множество вариантов архитектуры за короткое время и без существенных затрат, характерных для построения опытных образцов и оценки надёжности путём организации опытной эксплуатации.

Предложенная математическая модель может быть использована для автоматизации проектирования многопроцессорных аппаратно -программных комплексов. На практике стремятся к тому, чтобы проектируемая система управления реального времени обладала наибольшей возможной надёжностью при условии, что затраты на её создание и эксплуатацию не превосходят выделенные средства. Таким образом, мы приходим к задаче условной или многокритериальной оптимизации, в которой целевая функция выражается через вероятности состояний, рассчитываемых в рамках предложенной модели. Несмотря на то, что для показателей надёжности многопроцессорного аппаратно -программного комплекса существуют аналитические выражения, данная задача оптимизации обладает рядом неудобных особенностей: оптимизируемые переменные являются дискретными, наличие единственного экстремума и удобных для оптимизации свойств (выпуклость) не гарантировано, а объём пространства поиска быстро растёт с ростом количества типов процессоров.

При решении подобных задач оптимизации хорошо зарекомендовали себя эволюционные методы оптимизации, например, генетический алгоритм [13], вероятностный генетический алгоритм [14] или асимптотический вероятностный генетический алгоритм [15], а также некоторые другие «вдохновлённые природой» методы оптимизации, например, метод роя частиц [16]. Недостатком методов эволюционной оптимизации является наличие у них большого количества настраиваемых параметров, которые могут существенно влиять на качество найденных решений. Причём разные наборы параметров могут быть эффективны для различных задач оптимизации. Таким образом, использование эволюционных методов оптимизации требует, как правило, экспериментирования и привлечения специалиста в области эволюционных методов оптимизации.

Для того, чтобы исключить этап подбора эффективного сочетания параметров, может использоваться самонастройка [17-18]. Самонастраивающиеся методы оптимизации используют несколько наборов параметров, вычислительные ресурсы (для простоты можно считать, что это количество вычислений целевой функции) между которыми распределяются в зависимости от качества получаемых с их помощью решений. В начале процесса оптимизации все наборы параметров получают одинаковые ресурсы. Затем наборы параметров, которые порождают лучшие решения, получают дополнительные вычислительные ресурсы за счёт тех, которые показывают себя хуже. Существует некоторая нижняя граница для выделяемых ресурсов, это делается для того, чтобы любой набор параметров мог проявить себя в будущем, когда условия изменятся, так как различные этапы оптимизации могут требовать различных значений параметров.

Исследование эффективности указанных методов оптимизации при решении задачи оптимизации надёжности многопроцессорных аппаратно-программных комплексов систем управления реального времени с мультиверсионным программным обеспечением и разнородными процессорами является возможным направлением дальнейших исследований.