Математическая модель нагрева асинхронного двигателя с короткозамкнутым ротором на основе эквивалентной тепловой схемы

А с и н х ронн ые двига тели с короткоз а м кн у тым ротором яв л яю тся н а и бо ле е ра с прос тра не нным ти пом эл е ктриче с к и х м а шин в эл е к троприв оде пром ы шл е н ных и тех но л ог иче с к их у с танов ок [1]. О с нов н а я д оля отк аз ов эл ек тродв игате л ей с в яз ана с в ых одом из с троя из ол я ц ии ста торной обм отк и [2–4 ], в ыз в а нной е е пе ре гре в ом в ре з у л ьтате непра в и л ь н о й экс п лу атаци и . В с в яз и с эт им в оз ни кает н еоб х од им ост ь а декв атно й оц ен ки тем пе ра т у ры о б м оток э л е ктрод в и гат е л я д л я оценк и с рока с лу жбы дви г ат ел я и ег о э н ер ге ти ч еск и х п о к азат елей . А на ли з лите ра т уры поз в о л яе т с дел а ть в ыв од о наличии большого ко л иче с тв а ра з ра бота н ны х м етодов оце н ки тем пе ра т у ры , ос нов а нны х ка к на прям ы х м е тодах , та к и на кос в е н ных , с прим енение м м ате м а тиче ского м оде л иров а н ия [5–7]. Наибол е е ра с прос тра нё н ным спос обом ра с че та яв ляетс я м е тод эквив ал ент ной те п л ов ой сх е м ы [8, 9], кото рый п оз в о л яет оце н ить те м пе ра т ур у n -го узла э л е ктр иче с кой м а ши ны в з ада н ный м ом е нт в ре мени при не из м е н ной на гр узке на в алу двигате л я. В да н ном с лу ча е сл ожнос т ь м оде л и опре дел яетс я кол иче с тв ом уз л ов [10, 11 ] с бол ьшим кол иче с твом входных параметров.

Т е пл ов ые м оде л и, пре дста вл е н ные в [3] и [7] сос тоят из бол ьшого кол ич е с тв а у з л ов , ч то з на чител ь но ус л ожняет проце с с м оде л иров ания, а такж е треб ует бол ьшое количе с т во в х одны х данны х , таких ка к ге ом е триче ские пара м е тры м а гнитно й и э л е ктр иче с кой це п и м а ш ин ы, бол ьши нс т в о кот ор ых по луч и ть в оз м ож но то л ько на с тади и проектиров а н ия. И з этого в оз ни к а е т не обх о дим ос ть упр още ни я м ате м атиче ской моде л и с сохранением ее ад екв атнос т и. Д л я ра с че та т е м пе ра т уры при из м еняющейс я на гр у з ке прим еняю т не ста ц иона р ные мод ел и на грева, которые о пис ы в а ются с ис те м ой диффере н ци а л ь ных урав нени й, в ос нов е которых л ежит урав нен ие тепл ов ого б ал анс а [12]. Отде л ьно стоит отметит ь тот фа кт, ч т о на с рок с лу ж бы д вигате ля и, с оотв е тс т в е н но, изол яц ии бол ьшое в ли яние ока зыв а ет кра тков ре м е н ное из м е не н ие на гр у зки на валу [13,14].

Постановка задачи

В данной работе была поставлена задача экспериментально подтвердить адекватность модели нагрева асинхронного двигателя с короткозамкнутым ротором на основе эквивалентной тепловой схемы.

В качестве основы эквивалентной тепловой схемы была взята математическая модель, предложенная в [15], состоящая из 10 основных узлов. Особенность данной модели является ее простота и наличие основных узлов, которые являются критически важными при оценке теплового состояния машины.

Данная модель была доработана путем учета потерь в роторе асинхронной машины, а также путем учета сопротивления внутреннего воздуха машины.

Общий вид уравнения, описывающего тепловое состояние i -го узла:

д^=p -1 ^ a=1^ n, ∂t i  ∑n=1  Ri,n

где ∂Θ _i – малое приращение температуры узла за время ∂ t ; P_i – мощность электрических потерь в узле, Вт; Θ _i –значение температуры узла, °С; Θ _n –значение температуры смежного (соседнего) узла, °С; R_{i , n} – тепловое сопротивление между i -м и смежным узлом.

Основные узлы двигателя, участвующие в расчете, представлены на рис. 1.

На рис. 1 представлены следующие узлы: 1 – корпус двигателя; 2 – статор; 3 – статорный зубец; 4 – статорная часть обмотки; 5 – лобовая часть обмотки; 6 – железо ротора; 7 – кольцо ротора; 8 – вал ротора; 9 – внутренний воздух; 10 – воздушный зазор.

На рис. 2 представлена расчетная схема эквивалентной тепловой схемы рассматриваемого двигателя.

В табл. 1 представлены тепловые сопротивления эквивалентной тепловой схемы.

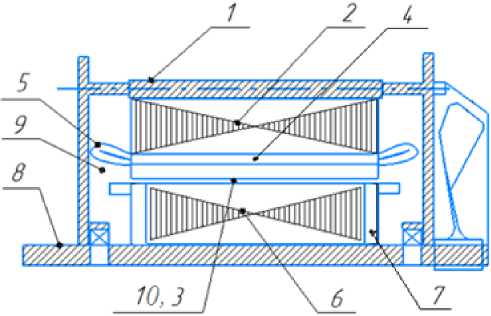
Рис. 1. Расположение расчетных узлов электродвигателя Fig.1. Location of the calculated units of the electric motor

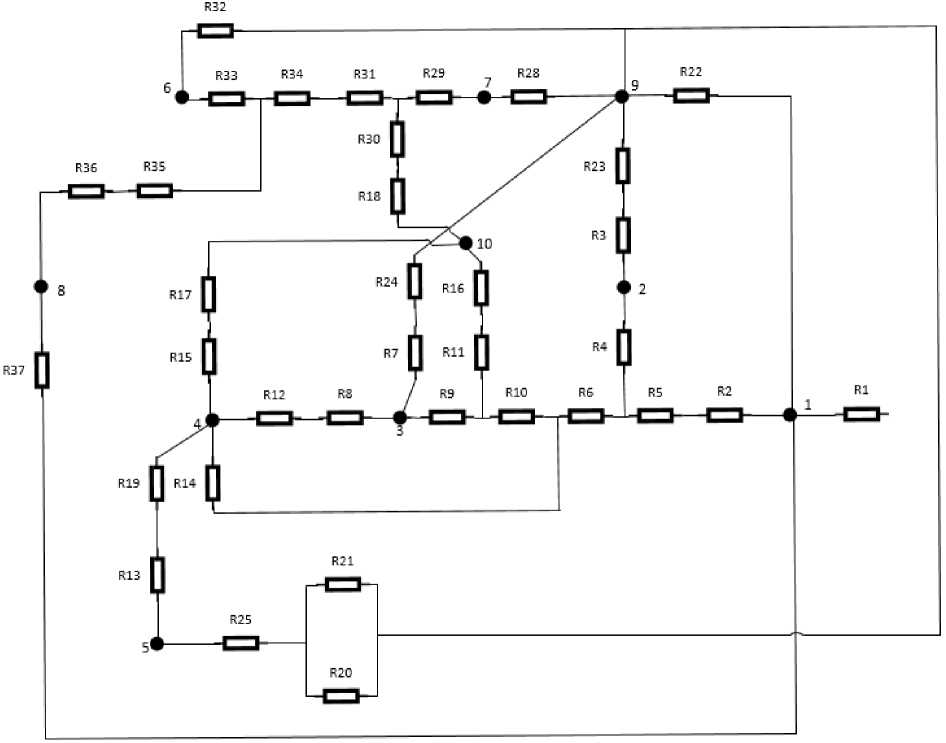
Рис. 2. Расчетная схема электродвигателя

Fig. 2. Calculation scheme of the electric motor

Таблица 1

Тепловые сопротивления эквивалентной схемы

Table 1

Thermal resistances of the equivalent circuit

Тепловое сопротивление	Элемент двигателя
R 1	Т е пл ов ое с опроти вление между корпусом машины и окружающим в оз д у х ом
R 2	Т е пл ов ое с опроти в л е н ие меж д у корп у с ом и с та тором
R 3	А кс иал ьное теп л ов ое с опротивл ение м е жд у ста тором и внутренним воздухом
R 4	Ра ди а л ьн ое те п л ов ое с опротивл е н ие с е рде чн ика с татора
R 5	Ра ди а л ьн ое те п л ов ое с опротивл е н ие от с та тора к корп у су
R 6	Ра ди а л ьн ое те п л ов ое с опротивл е н ие м е ж д у зу бц ом и статором
R 7	А кс иал ьное теп л о вое сопротивление между зубцом и внутренним воз д у х ом
R 8	Ра ди а л ьн ое те п л ов ое с опротивл е н ие от зуб ца к ста тор у
R 9	Ра ди а л ьн ое те п л ов ое с опротивл е н ие зубца статора
R 10	Ра ди а л ьн ое с опроти в л е н ие от зуб ца с та тора к с е рде чн и к у с татора
R 11	Ра ди а л ьн ое те п л о вое сопротивление между зубцом и воздушным за з ором
R 12	Ра ди а л ьн ое те п л ов ое сопротивление между статорной обмоткой и статором
R 13	А кс иал ьное теп л о вое сопротивление между статорной частью обмо тки и л обов о й
R 14	Ра ди а л ьн ое те п л о вое сопротивление от статорной обмотки до стато ра

Окончание табл. 1

Table 1 (end)

Тепловое сопротивление	Элемент двигателя
R 15	Радиальное тепловое сопротивление между статорной обмоткой и воздушным зазором
R 16	Радиальное тепловое сопротивление от воздушного зазора до зубца статора
R 17	Радиальное тепловое сопротивление от воздушного зазора до статорной обмотки
R 18	Радиальное тепловое сопротивление от воздушного зазора до ротора
R 19	Аксиальное тепловое сопротивление от лобовой части обмотки до статорной части
R 20	Тепловое сопротивление между лобовой частью обмотки и внутренним воздухом
R 21	Тепловое сопротивление между лобовой частью (серединой) обмотки и внутренним воздухом
R 22	Аксиальное тепловое сопротивление между внутренним воздухом и корпусом
R 23	Аксиальное тепловое сопротивление между внутренним воздухом и статором
R 24	Тепловое сопротивление от внутреннего воздуха до зубца статора
R 25	Тепловое сопротивление от внутреннего воздуха до лобовой части обмотки
R 28	Аксиальное тепловое сопротивление между стержнями ротора и внутренним воздухом
R 29	Аксиальное тепловое сопротивление стержней ротора
R 30	Радиальное тепловое сопротивление от стержней ротора до воздушного зазора
R 31	Радиальное тепловое сопротивление между стержнями ротора и железом
R 32	Аксиальное тепловое сопротивление между железом ротора и внутренним воздухом
R 33	Радиальное сопротивление железа ротора
R 34	Радиальное сопротивление от железа ротора до стержней
R 35	Радиальное тепловое сопротивление между ротором и валом
R 36	Радиальное тепловое сопротивление от вала до ротора
R 37	Аксиальное тепловое сопротивление между валом и подшипниками

Обобщенная формула для нахождения теплового сопротивления элемента двигателя имеет вид [3]:

g -М T - D ад³

V ²

R = ——, a-e-S

где l – длина или толщина элемента машины; a - коэффициент конвективной теплоотдачи; e - коэффициент теплового излучения; S - площадь элемента машины, м².

При этом коэффициент конвективной тепло-

где g - ускорение свободного падения; р - коэффициент объемного расширения; V - кинематический коэффициент вязкости; Pr – число Прандтля:

Pr = —, K

где K – коэффициент температуропроводности:

отдачи для воздуха рассчитывается по следующим формулам [11]:

1 V

a = ^а возд D ад

1,36 - 0,518 - Ra⁶

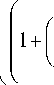
. 2.) 0,559 >б

Pr J

где а _возд - теплопроводность воздуха при 20 °С;

D _ад – эквивалентный диаметр машины, м²; Ra – число Рэлея:

K = —,                         (6)

c -Р где у - коэффициент теплопроводности; c - удельная теплоемкость воздуха, Дж/К; р - плотность воздуха, кг/м³.

Приращение температуры A T для каждого узла определяется по формуле

A T = G ^{- 1} -A P ,                             (7)

где G ^{- 1} - обратная матрица проводимостей [15]; A P - матрица потерь двигателя, которая скла-

дывается из потерь в железе статора, активных потерь обмотки статора, а также добавочных потерь.

Матрица проводимостей в общем виде имеет

вид	n ^ i = 1 R 1, i	1 — . R 1,2	1 Л — .. R 1, n
G =	- JL R 2,1	n ^     . i = 1 R 2, i	1 — .. R 2, n	,           (8)
	... - V   Rn J	...          . 1 — . R n ,2	..          ... n .. ^ i = 1 Rn , i 7

Элементы матрицы определяются по формулам, представленным в [11, 15].

Потери в электродвигателе A P определяются по формулам (9)–(15):

Потери в обмотке статора A P ost , Вт [8]:

A P ost = 3 ■ 1 st ■ R st ,                                 (9)

где I_st – ток статора, А; R_st – активное сопротивление обмотки статора, Ом.

Потери в стали статора A P_st , Вт [8]:

^{A P}st = ^p 1,0/50 ^-

r a■ f i

V 7

x | k_n_ ■ B ² ■ m„ + к. ■ B² ■ m _, ), да да a    д z   z ср     z 1

где p1 0/50 = 2,5 - удельные потери при индукции 1 Тл и частоте перемагничивания 50 Гц, Вт/кг [8]; fl - частота, Гц; Р - показатель степени, учитывающий зависимость потерь в стали от частоты перемагничивания, р = 1,4 [8]; кда и кдz - коэффициенты, учитывающие влияние на потери в стали неравномерности распределения потока по сечениям участков магнитопровода и технологических факторов; кда = 1,6 - для машин мощностью меньше 250 кВт [8]; кд_ = 1,7 - для машин мощ- ностью меньше 250 кВт [8]; Bдa и Bzср – индукция в ярме и средняя индукция в зубцах статора; ma – масса стали ярма:

m a = ^п ■ ⁽ D a - h a ) ^- h a ^{- 1} ст1 ^{- k} с1 ^- У c , ⁽¹¹⁾ где D _a – внешний диаметр статора, м; l _ст1 – длина статора, м; к _с1 - коэффициент скоса паза; y c -удельная масса стали; h _a – высота ярма статора:

h a = 0,5 ■ ( D a — D ) - h п 1 , (12) где D – внутренний диаметр статора, м; h _п1 – высота паза, м; m_{z 1} – масса зубца статора:

m z 1 = ^hZ 1 ■ b z 1ср ■ ^Z 1 ■ ¹ ст1 ■ ^к с1 ■ У с , ⁽¹³⁾ где h_{z 1} – расчетная высота зубца статора, м; b_{z 1ср} – средняя ширина зубца статора:

г _ bz 1max ⁺ b z 1min b z 1ср =         2        ’

Потери в короткозамкнутом роторе A P_rot , Вт [8]:

AProt = Z2 ■ lot ■ R., (15) где Z2 – количество стержней в роторе, шт.; Irot – ток ротора, А; Rrot – сопротивление корот- козамкнутого ротора (стержни и кольца), Ом.

A P dob - добавочные потери принимаем в 5–8 раз меньше основных [8].

После расчета основных и добавочных потерь составляется вектор-столбец основных и добавоч- ных потерь [15]:

A P st

A P st + 0,3 .A P do _b

0,48 .A P _;t + 0,4 -A P dob

0,52 .A P ost

A P =

V

.

Для проверки математической модели был собран стенд, на котором проводилось измерение температуры обмоток двигателя при различных режимах работы.

Постановка эксперимента

Для измерений был выбран асинхронный двигатель АИР100L4ПРУ3 с номинальной мощностью 4 кВт и скоростью холостого хода 1410 об/мин. Корпус двигателя и боковые крышки выполнены из чугуна, схема соединений обмоток – звезда, класс нагревостойкости изоляции – F. Эксперимент проводился при температуре окружающего воздуха 24–25 °С. В качестве нагрузочной машины выступал двигатель постоянного тока мощностью 1,9 кВт с возможностью регулирования момента в необходимом диапазоне. Во время эксперимента поддерживалось значение момента нагрузки 18 Н·м.

Эксперимент проводился в следующем порядке: подавалось напряжение на асинхронный двигатель, в течение 2–3 с он выходил на режим холостого хода, затем включалась нагрузочная машина, на котором при помощи встроенного индикатора выставлялся момент на валу. В течение 15 мин происходила нагрузка асинхронного двигателя, этого времени было достаточно для достижения температурой установившегося режима.

О тк л юче н ие сте н да происходил о в о бра тном п орядке с о д нов ре м ен н ы м с ня тие м пока з ани й те мпературы.

К онтрол ь темп ера т уры корп ус а д в игате ля и его обм оток п ро и з в оди л с я при пом ощи д ву х темпе рат ур ных да тч иков , у с танов л енны х в ста торной и л обов ой ча с т и обм оток, а также п ри пом ощи тепловизора.

На рис. 3 показана терм ограм м а дв ига тел я, на которой отче тл и в о в и дно нагре т ую л о бовую ч а с ть обмотки, зубцы статора.

Экс пе рим ентал ьные да н ные был и с ра внены с результатами моделирования и пре дс тав л е н ы н а рис. 4, 5.

В табл. 2 и 3 представлены результаты моделирования и эксперимента с расчетом относительной погрешности температуры для каждого узла машины.

По результатам эксперимента видно, что наименьшая погрешность температуры наблюдается в статорной и лобовой части обмотки двигателя. Это вызвано следующими факторами: в модели достаточно корректно учтены активные потери в обмотке статора, учитывается обмен теплоты как со статорным железом, так и внутренним воздухом. Результаты моделирования также подтверждают результаты работ [16–18], в которых указано, что температура лобовой части обмотки выше температуры

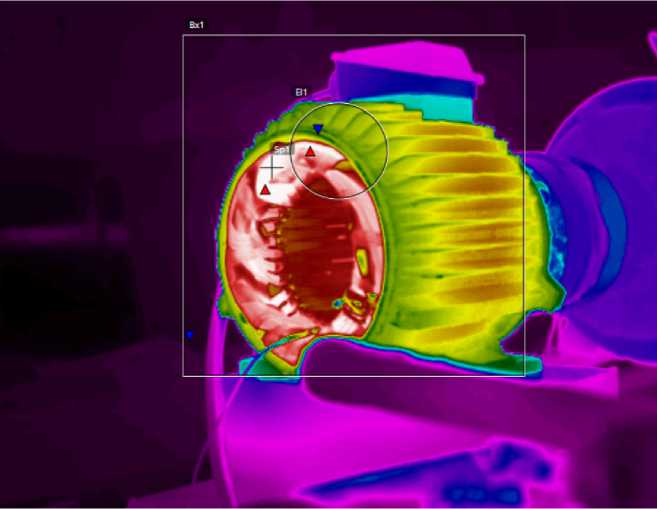
Рис. 3. Контроль температуры обмоток электродвигателя тепловизором

Fig. 3. Monitoring the temperature of the motor windings with a thermal imager

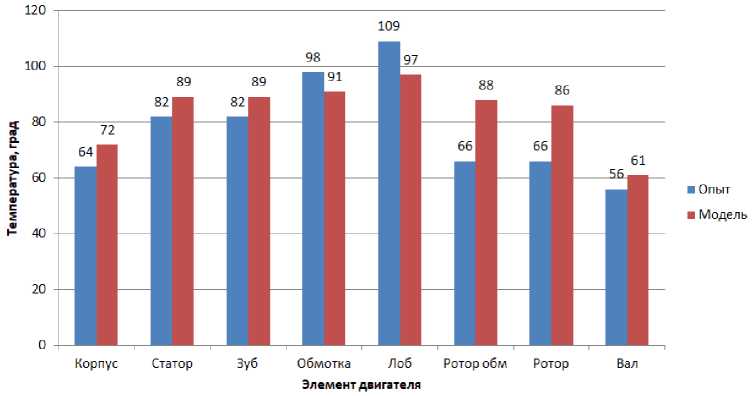
Рис. 4. Сравнение результатов эксперимента и моделирования при работе двигателя на холостом ходу

Fig. 4. Comparison of the results of the experiment and simulation for the engine idling

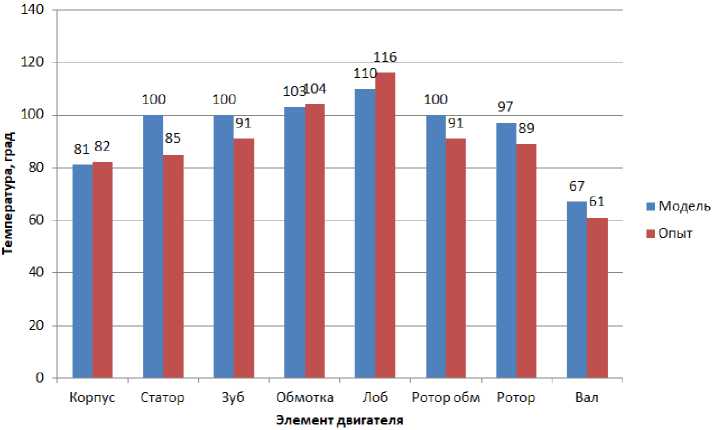
Рис. 5. Сравнение результатов эксперимента и моделирования при работе двигателя под нагрузкой

Fig. 5. Comparison of the results of experiment and simulation when the engine is running under load

Таблица 2

Сравнение результатов моделирования и эксперимента при работе двигателя под нагрузкой

Table 2

Comparison of simulation and experiment results when the engine is running under load

Узел	Мод ел ь, °С	Эксперимент, °С	Погрешность, °С	Погрешность, %
Корпус	8 1	82	1	1,2
Статор	1 00	85	15	15
Зубец статора	1 00	91	9	9
Статорная часть обмотки	1 03	104	1	0,96
Лобовая часть обмотки	1 10	116	6	5,17
Короткозамкнутое кольцо ротора	1 00	91	9	9
Железо ротора	9 7	89	8	8,24
Вал	6 7	61	6	8,95

Таблица 3

Сравнение результатов моделирования и эксперимента при работе двигателя на холостом ходу

Table 3

Comparison of the results of simulation and experiment when the engine is idling

Узел Модель, °С Эксперимент, °С Погрешность, °С Погрешность, % Корпус 72 64 8 11 Статор 89 82 7 7,8 Зубец статора 89 82 7 7,8 Статорная часть обмотки 91 98 7 7,1 Лобовая часть обмотки 97 109 12 11 Короткозамкнутое кольцо ротора 88 66 22 25 Железо ротора 86 66 20 23,2 Вал 61 56 5 8,1 обмотки, уложенной в пазах статора. При этом потери в статорном железе и добавочные потери имеют свою погрешность, связанную с магнитными характеристиками машины. Наибольшие отклонения модели от экспериментальных данных наблюдаются в роторной части машины. Это обусловлено невозможностью снятия всех геометрических параметров ротора [3].

Выводы

• 1.    Экспериментальные данные подтверждают результаты математического моделирования, что позволяет применять метод ЭТС для определения температуры обмоток электродвигателя с достаточной точностью в решении прикладных задач. Для улучшения результатов необходимо учесть

• 2.    Увеличение количества узлов модели позволит получить более дифференцированные данные по температуре электродвигателя.

• 3.    Рассмотренная модель нагрева асинхронного двигателя демонстрирует хорошие результаты для стационарных режимов работы с неизменной нагрузкой. Для оценки изменения температуры при изменении нагрузки необходимо применять нестационарные модели, в основе которых лежит тепловой баланс машины: применяемый метод ЭТС в данном случае должен быть сильно изменен.

механические потери, более качественно учесть активные потери в роторе. Однако для частей двигателя, не связанных с ротором, точности исследованной модели достаточно.