Математическая модель напряженной магнитоанизотропной структуры устройства телеметрии силового воздействия

шары 4 растягивается образуя напряжение растяжения σр [1, 2].

Под действием механических напряжений σ_с и σ_р магнитная проницаемость ЧЭ2 уменьшается, а магнитная проницаемость ЧЭ3 увеличивается, согласно теории ферромагнетизма [1, 2], что приводит к изменению частоты выходных сигналов f ₁ и f ₂ генераторов Г1 и Г2. Эти сигналы с выхода обмоток 7, 8 ЧЭ 2, 3 подаются на входы смесителя См. С выхода смесителя См сигнал разностной частоты поступает на антенну А2 передатчика и принимается антенной А1 приемника, где обрабатывается усилителем разностной частоты УРЧ, амплитудным ограничителем АО, частотным детектором ЧД с гетеродином ГТ и подается на регистрирующий прибор РП, фиксируя силовое воздействие.

Обобщенная физическая модель НМАС ЧЭ сжатия 2 и растяжения 3 представлена на рис. 2 в виде четверти ферромагнитного кольца, сечение которого ориентировано в сферической полярной системе координат таким образом, чтобы вектор нормальных напряжений σ совпадал с направлением магнитного поля Н _С, а вектор касательных напряжений σ был с ним перпендикулярен, где Р _С – сила воздействия на кольцо направлена по радиусу ЧЭ под прямым углом к полю Н _С; а = r _н – r _в – толщина кольца; r _н, r _в – наружный и внутренний радиусы кольца; b – ширина кольца; r ₀ – средний радиус элемента; φ – угол между осью симметрии сечения и радиусом r _в; E_r и E_b напряженности электрического поля на гранях сечения; B _С – магнитная индукция внешнего электромагнитного поля; Н _С – напряженность магнитного поля в сечении кольца; i – ток, протекающий через обмотку возбуждения; i _в – вихревой ток; θ – угол

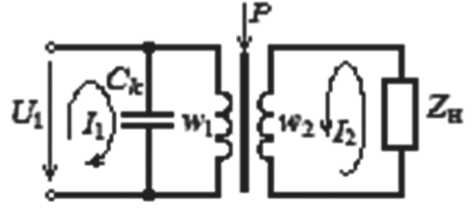
Рис. 3. Схема замещения магнитной цепи упругих элементов

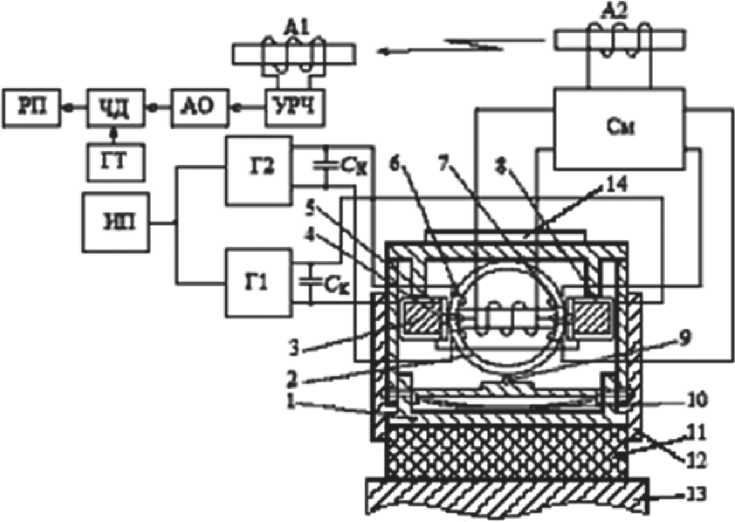
Рис. 1. Структурная схема устройства телеметрии силового воздействия

между осью симметрии сечения и радиусом r 0 по длине кольца с в радианах.

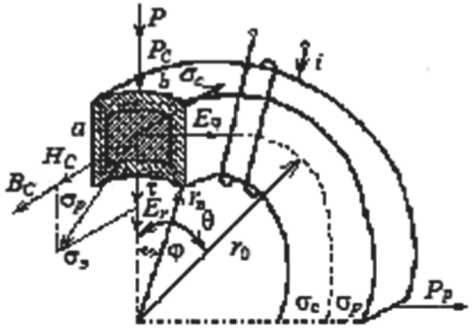
Рис. 2. Обобщенная физическая модель НМАС ЧЭ

• 1.    Картина электромагнитного поля в любом сечении кольцевого ЧЭ равномерна и не зависит от угла 9.

• 2.    Магнитная индукция B _С электромагнитного поля, в котором находится ЧЭ, изменяется по

• 3.    Картина силового поля с учетом напряжений сжатия, растяжения и сдвига зависит от угла 9 ЧЭ и может быть рассмотрена с использованием

синусоидальному закону и имеет только нор-

мальную составляющую.

3-й гипотезы прочности [1].

Общее выражение для определения нор-

мальных механических напряжений сжатия и

растяжения в кольцевом ЧЭ под действием силы

нажатия Р записывается в виде [1]:

^ Н, b =

0,5 P ba

±3,82 r - +1 6 r^ +11 Cos 9 a I a )

, (1)

Математическая модель обобщенной физической модели НМАС описывается дифференциальными уравнениями теорий электромагнитного поля, ферромагнетизма и упругости в полярных координатах. При этом принимаются следующие допущения и предположения.

где верхние знаки относятся к наружной поверхности кольцевого ЧЭ, а нижние знаки - к внутренней поверхности ЧЭ.

При 9 = 0 наружная поверхность ЧЭ сжимается под действием ст_с а внутренняя - растягивается под действием ст р (см. рис. 2). При 9 = п/2 картина меняется на обратную: наружная поверхность растягивается под действием ст_р, а внутренняя сжимается под действием ст_с. Картина распределения напряжений повторяется для каждой четвери кольца.

Механические напряжения растяжения ст_р ЧЭ2 при 9 = п/2 являются причиной возникновения силы растяжения Р _Р кольцевого ЧЭ3, который расположен во взаимно перпендикулярной плоскости - рис. 1. При этом внутренняя поверхность ЧЭ3 сжимается, а наружная - растягивается, т. е. картина распределения механических напряжений ст_с и ст_р аналогична ЧЭ2.

Используя обобщенную физическую модель ЧЭ на рис. 2, определяются максимальные напряжения сжатия с с при 9 = 0 и растяжения ст р при 9 = π/2 согласно выражению (1):

1,1- P - r          1,91- P - r

° =----г^-0 ° р =----2—⁰

ba ²              ba ²

;

.

Учитывая третью гипотезу прочности для ЧЭ °_э = V ° ² + 4т ² и максимальные касательные напряжения т = (ст р - с_с)/2, определяются эквивалентные механические напряжения при работе ЧЭ2 на сжатие и ЧЭ3 на растяжение:

эс           с р        с р сэр = V2сР + с2 - 2срсс •       (3)

4. Под действием эквивалентных механических напряжений сжатия сэс и растяжения сэр магнитная проницаемость ЧЭ2 уменьшается, а ЧЭ3 – увеличивается [1].

Нэс , р = Рн ±^{Н          (4)}

где (–) – при сжатии элемента 2; (+) – при растяжении элемента 3; μн – начальная магнитная проницаемость элементов 2 и 3; ∆μ – изменение магнитной проницаемости.

При принятых допущениях и предположениях при одновременном воздействии силового поля сжатия или растяжения и поля возбуждения состояние соответствующего ферромагнитного ЧЭ описывается дифференциальными уравнениями в сферических полярных координатах [1]:

д Н_с д r

= У_Ф E _Ф ;

д Н_с дф

= Y rEr ;

д Er д Е ф д Вс ^^^^^^^^^^^^^^^^^^^^^^^^^^. ^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^_ ^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^_ д r дф д t

- jюp ° H_c ^;

дВ_г _ 1 д В_г I д Н_г  д Н_г  д Н_г

-^- +   =C-I ^=C + ^=C + вHc В2 дНс I д°   д.   Вт

C    Cp   c

E (w + ^ w L ° .

(д r   дф де ) ^э

где с_э - соответствующие эквивалентные напряжения кольцевых ЧЭ; у _r , у_ф удельные электрические проводимости по направлениям; E r , E _ф; H C - комплексы действующих значений напряженностей электрического и магнитного полей по поверхности сечения кольца по переменным r , ф и 9; с - длина кольца; r ₀ - средний радиус элемента; ю - круговая частота; ц_сэ - магнитная проницаемость от механического напряжения с_э; w, , w _ф, w ₉ - перемещение точек структуры по радиусу r , углам ф и 9; Е - модуль упругости; 9 - угол в радианах.

Граничные условия в этом случае имеют вид (рис. 2).

Н_с ( r, ф ) = Н_с ( r ) при r = r 0 ± а/ 2, ф = 0; r _в<  r ^ r _н; (8)

^Н С (ф, r ) = ^Н С (ф) при bb - arcsin — < ф < arcsin —        (9)

2 r í                2 r â

Ф 2 при малых углах ф b « L = J r ₀ d ф .

Ф 1

b

Н_с ( r ,ф) = 0 при ф = ±arcsin— ;

2 r _â

Н_с (ф, r ) = 0 ; при r = r ₀ ± а/ 2.            (10)

c = J r ₀ d 9 = r ₀9 ; 0 < 9 < 2n.              (11)

Уравнение теории упругости (7) рассмотрено с учетом 3-й гипотезы прочности, и его решение представлено в виде формул (3). Уравнение ферромагнетизма (6) для НМАС решено исходя из плотности свободной энергии ферромагнетика и термодинамических соотношений для обратимых магнитомеханических процессов при растяжении-сжатии, что позволило определить магнитные проницаемости ЧЭ цс их изменения при статических и динамических воздействиях P и P(t) [1]:

K '_{с р} ^a_s ² ц_н’ r₀P

Р. = Нн ±ДР; Н° = НН ±   • ^2ba2    ^12> где K’с, р – коэффициент при сжатии и растяжении; Xs - изотропная магнитострикция материалаЧЭ; as коэффициент намагниченности материала.

Из решения уравнений электромагнитного поля (5) при выбранных граничных условиях (8) – (11) определены плотности токов, вихревые I _В и намагничивающие I _Ф токи и сопротивления этим токам Z _В и Z _Ф [1]. Последнее зависит от силового воздействия и имеет вид:

Z ф= \р. +

У

K 'с,р ^S«S н Н ^r0^рЛ

пВ ² ba ²

K П ej , (13) )

где S _э = 2( a + b ) a_В – сечение эквивалентного контура; a_В – глубина проникновения магнитного поля в материал; a - угол сдвига между намагничивающим током I Ф и магнитным потоком Ф; K _П = K _Т – коэффициент трансформации.

Выражение (13) позволяет определить электрические потери и угол магнитных потерь в ЧЭ при силовых воздействиях. На рис. 3 показана схема замещения ЧЭ, НМАС которых работает при сжатии-растяжении.

Для схемы замещения по втором у закону Кирхгофа и после перехода к магнитным индукциям и далее к напряженностям поля система алгебраических уравнений преобразуется к виду:

H_ХД_Х - H 2 Д 2 к

^^^^^^^^

T r ^ ) ^² S' Ck w 2 J

U 1 toSw ^

^^^^^^^в

H х Д х + H 2 Д 2 к

^^^^^^^в

2S^_ mSCw2 J

= 0

.

В результате решения системы уравнений определяется напряженность магнитного поля H ₂ и выходные действующие напряжения U _Н на Z _Н с выхода обмоток 7, 8 – рис. 1.

H = ^U 2 ^Ckw^

^{2        r}o 9

г

^Д н ± к

^K 'с,р ^2 Д 2 ^Г 0 ^P^

пВ ² ba ²

J

H ² r 0 0

U н 7,8     2^н

,               _{w 2}

г

= U 2 ^ р.с C К K t Дн ±-к

Zн

K 'с,р <а Д 2 Г о P )

nB ² ba ²    ₇

Изменение магнитных проницаемостей (12) магнитных элементов 2 и 3 приводит к изменению индуктивности обмоток возбуждения 5 и 6 и изменению частот генераторов Г1 и Г2 [1].

f Г 1, Г 2

2 n ba ² w 2 C k

r ₀

^Д ± к

K с,р ^а .Д . Г о P )

п В ² ba ²

в 1

, (16)

J_

где w ₁ – число витков обмоток возбуждения 5, 6 элементов 2, 3; C _к – емкости контурных конденсаторов генераторов Г1 и Г2.

Частоты f _Г1 и f _Г2 генераторов Г1 и Г2 через измерительные обмотки 7, 8 подаются на входы смесителя См, с выхода которого сигнал ∆ U _н = U _н7 – U _н8 частотой ∆ f = f _Г1 – f _Г2 поступает в антенну А 2 передатчика и принимается антенной А 1

приемника, где обрабатывается и подается на регистрирующий прибор РП.

Все узлы передатчика и приемника выполнены на интегральных микросхемах.

Предлагаемая методика расчета использовалась для УТСВ со следующими параметрами:

• 1.    элемент 2 сжатия 5×3×1,5 мм из феррита 2000 НМ1 w ₁ 20; w ₂ = 10; K _Т = 2; Z _н = 1×10⁴ Ом, C_k = 90 пФ; μ_н = 25·10⁴ Гн/м; U ₁ = 5B – напряжение генератора Г1.

• 2.    элемент растяжения 3 10×6×3 мм из феррита 2000 НМ1; U ₁ = 5B – напряжение генератора Г2 w ₁ 30; w ₂ = 15; K _Т = 2; Z _н = 1×10⁴ Ом, C _к = 42 пФ; μ_н = 28·10^–4 Гн/м.

В результате расчета получено:

• 1)    при Р = 0 f _Г1 = 1,5×10⁶ Гц; U _н7 = 210 мВ; f _Г2 = 1×10⁶ Гц; U _н8 = 73 мВ; на выходе смесителя См в А 2 ∆ f = 0,5 МГц; ∆ U _н = 137 мВ; f _РП = ∆ f = f _ГТ = 0;

• 2)    при Р = 30 Н f _Г1 = 1,8×10⁶ Гц; U _н7 = 150 мВ; f _Г2 = 0,95×10⁶ Гц; U _н8 = 80 мВ; на выходе смесителя См в А 2 ∆ f = 0,85 МГц; ∆ U _н = 70 мВ; f _РП = ∆ f – f _ГТ = 0,35 МГц; U _РП = 2,0 В.

Экспериментальные исследования подтвердили правильность теоретических положений и формул – погрешность не превышает 10%.