Математическая модель нестационарного процесса компрессионного формования пластин из гранулята термопластичных композитов

Одним из традиционных методов переработки высоконаполненных полимерных композиций является компрессионное формование1-2, заключающееся в пластической деформации материала при действии на него температуры и давления и последующей фиксации формы изделия. Метод широко применяется также при переработке композиционных материалов с металлической и керамической матрицей.

С точки зрения технологии компрессионного формования, надежность полимерного изделия в эксплуатации определяется прежде всего

• ¹    Производство изделий из полимерных материалов : учеб. пособие / В. К. Крыжановский [и др.]. СПб. : Профессия, 2008. 464 с.

• ²    Современные технологии получения и переработки полимерных и композиционных материалов : учеб. пособие / В. Е. Галыгин [и др.]. Тамбов : Изд-во ФГБОУ ВПО «ТГТУ», 2012. 180 с.

однородностью его структуры и значениями физико-механических характеристик, а также точностью размеров, которые, в свою очередь, зависят от величины усадки полимера, конструкции пресс-формы, соотношения масс детали и заготовки, геометрии последней и технологических параметров ведения процесса (температуры и длительности нагрева заготовки и охлаждения сформованного изделия, давления формования и др.). Это определяет необходимость развития теории процессов компрессионного формования, в частности, из гранулята термопластичных композитов.

Целью исследования является разработка математической модели компрессионного формования плит из гранулята высоконаполненных термопластичных композитов, позволяющей на стадии проектирования технологического процесса и формующей оснастки рассчитывать комплекс оптимальных параметров, обеспечивающих получение высококачественных изделий.

Обзор литературы

Ранее в научных работах [1–2] были предложены неизотермические и нестационарные математические модели компрессионного формования эластомерных композиций с реологическими свойствами, описываемыми степенной зависимостью. При разработке данных моделей были приняты допущения о соответствии размеров сплошной заготовки размерам формующей полости и независимости теплофизических характеристик композиции от температуры. Модель позволяет рассчитать методом конечных элементов изменение температуры композиции и давления в полости пресс-формы в течение времени формования, учитывает истечение избытка расплава в облой вследствие температурного расширения.

Том 27, № 4. 2017

В работе [3] приводится более совершенная модель компрессионного формования, позволяющая рассчитать методом конечных элементов параметры процесса при произвольной конфигурации упруговязкой сплошной заготовки с реологическим поведением, описываемым моделью А. И. Леонова [4]. Недостатком модели является допущение о независимости теплофизических характеристик композиции от температуры.

В работах [5–6] предложена математическая модель объемного прессования плит из дисперсной термопластичной заготовки, реологические свойства которой описываются моделью упруго-пластичного тела. Для расчета теплопроводности использована теория обобщенной проводимости Г. Н. Дульнева3. Модель позволяет описать стадии сжатия пористой заготовки, ее нагрева и охлаждения сформованной плиты. Однако в цитируемых работах отсутствуют сведения о методе реализации модели, включающей более 30 уравнений, и проверке ее адекватности.

В ранних работах Б. Д. Руденко [7–8] исследовано влияние содержания полимерного связующего, а также вида и влажности древесного наполнителя на упруго-прочностные характеристики древесно-полимерных плит, получаемых методом компрессионного формования. К недостаткам работы следует отнести отсутствие сведений о влиянии технологических параметров формования (температуры, давления и длительности процесса) на указанные характеристики.

В более поздних работах указанного автора [9–11] поставлена задача построения математической модели процесса компрессионного формования древесно-полимерных плит, которая основывается на уравнениях переноса энергии в композиционном материале, отверждения полимерной матрицы и термовязкоупругости. Достоинством работы [12] является то, что в ней сформулирован критерий завершения процесса прессования, в качестве которого выбрана энергия деформирования при прессовании. Недостаток – отсутствие описания методов реализации предлагаемой модели и проверки ее адекватности.

В работе [13] сформулированы общие подходы к решению задачи построения корректной математической модели плоского горячего прессования композиционных материалов на древесных наполнителях. Отмечается, что адекватная математическая модель должна содержать уравнения, описывающие изменение в течение прессования давления, температуры, степени отвердения связующего, влажности, плотности, коэффициентов теплопроводности, теплоемкости и проницаемости наполнителя. Подчеркивается важность установления условий формирования адгезионной и когезионной прочности композита в процессе прессования. При этом в работе отсутствуют данные об используемом в модели реологическом уравнении и методах решения предлагаемой системы уравнений.

Основная задача, которой посвящена работа [14], состоит в методике определения реологического уравнения для описания деформационного поведения древесно-стружечных плит на основе экспериментальных данных и теоретических расчетов. Предполагается, что в любой момент времени общая деформация является суммой четырех составляющих – упругой, вязкой или упруго запаздывающей, остаточной и температурно-влажностной. Приводится система урав-

MORDOVIA UNIVERSITY BULLETIN нений, количественно описывающих реологические свойства древесного композита.

В работе [15] построена изотермическая конечно-элементная модель прессования (твердофазного формования) высоконаполненных полимерных систем при температуре ниже температуры плавления. Авторами показана возможность использования для описания реологического поведения подобных систем степенного уравнения Оствальда. Из анализа кривых формования следует, что твердофазное компрессионное прессование высоко-наполненных полимерных композиций представляет собой сложный процесс комбинации течения и уплотнения наполненного материала.

Таким образом, общим недостатком процитированных работ является отсутствие сведений о методах реализации разработанных математических моделей и проверки их адекватности. Кроме того, в моделях не учтена зависимость давления в полости пресс-формы от истечения избытка расплава в облой, не поставлена задача расчета размеров формующей полости при заданных размерах изделия с учетом компрессионной и термической составляющих его усадки. Перечисленные модели также не содержат полного описания всех стадий процесса.

Материалы и методы

В представленной математической модели для решения задачи построения нестационарного температурного поля в плитах пресс-формы и формуемом полимерном композите, характеризующемся изменением физических состояний и зависимостью коэффициента температуропроводности от температуры, использовано решение А. В. Лы-кова4 для задачи нагрева (охлаждения) полуограниченной пластины из мате- риала с постоянными теплофизическими коэффициентами при переносе тепла теплопроводностью. Для учета температурной зависимости теплофизических коэффициентов полимерного композита разработана итерационная процедура, реализованная в программе Simulation Molding Plates5. Для расчета температурных функций теплофизических коэффициентов композитов, состоящих из полимерной матрицы, наполнителей и модификаторов с известными коэффициентами, использована теория Г. Н. Дульнева. Для описания изменения давления в полости пресс-формы на стадиях нагрева композиции и охлаждения готового изделия использовано модифицированное уравнение Ван-дер Ваальса6.

Результаты исследования

Анализ экспериментальных результатов показывает, что процесс компрессионного формования пластин из гранулята композиционных материалов в пресс-форме закрытого типа (рис. 1) является нестационарным и неизотермическим и может быть разделен на три принципиально различающиеся стадии.

На первой стадии (сжатия гранулята длительностью t ₁) навеска гранулята с начальной температурой T _г и массой на 3–5 % большей массы формуемой пластины засыпается в полость раскрытой пресс-формы, предварительно нагретой до температуры формования T _ф = (1,10–1,20) T _вт, где T _вт – температура прехода формуемого материала

Том 27, № 4. 2017

в вязкотекучее состояние. Гранулят из-за порозности занимает в пресс-форме высоту h _п0 (рис. 1, а). В момент времени t = 0 к плунжеру 4 прикладывается усилие прессования F _п, приводящее к замыканию пресс-формы с созданием напряжений σ _: на контактных площадках и уплотнению гранулята при давлении p _с. При этом воздух из пресс-формы отжимается через каналы 2 и зазор 3 в атмосферу, а контактирующая с пресс-формой поверхность гранулята принимает температуру пресс-формы T _ф. Стадия заканчивается в момент t = t ₁, когда значение пороз-ности гранулята ε становится равным 0 (рис. 1, б).

На начальном этапе второй стадии (нагрева и формования расплава длительностью t ₂) до момента t < ( t ₁ + t ₂) происходит нагрев гранулята со скоростью, определяемой величиной коэффициента температуропроводности сжатого гранулята a ₃( T ) , с образованием переменного температурного поля T 3 ( t , z ) .

При достижении температуры T _вт фазового перехода композиции в вязкотекучее состояние в областях, прилегающих к поверхностям плунжера и матрицы, начинается образование расплава 8 (рис. 1, в). С течением времени нагрева происходят перемещение фронта расплава, определяемого координатой z _г( t ), и снижение толщины гранулята. В момент времени t <  ( t ₂ + t ₁) весь объем гранулята переходит в расплавленное состояние.

Ι

ΙΙ

ΙΙΙ

".   14 J

]=.=■ -I

6) If л J J - ti f . ^

I 2 1 J 5

\ I । T* edeei

"Ifd J

(|>-^1

rtf

1^-Jit

Гм. const

"TT™

Ct f “Ui I if Jj]

10 J t

JlHi । ti f th ' f:' hl

Tri. * const

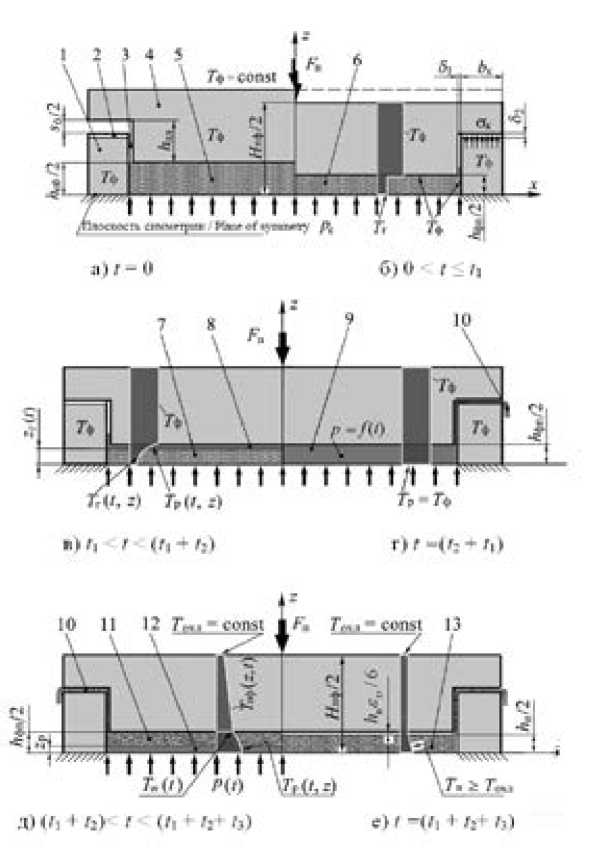
Р и с. 1. Расчетные схемы и температурные профили по стадиям процесса компрессионного формования пластин из гранулята термопластичных композитов: I – начальный (а) и конечный (б) этапы стадии сжатия гранулята; II – начальный (в) и конечный (г) этапы стадии формования расплава; III – промежуточный (д) и конечный (е) этапы стадии охлаждения расплава; позиции схемы: 1 – матрица; 2 – каналы для отвода воздуха и избытка расплава; 3 – зазор между плунжером и матрицей; 4 – плунжер; 5, 6 – гранулят до и после сжатия; 7 – зона нагретого гранулята; 8 – расплав композита; 9 – сформованный расплав; 10 – облой (грат); 11 – застекловавшаяся часть расплава; 12 – остаточная часть расплава;

13 – сформованное изделие (пластина)

F i g. 1. Calculation outlines and temperature profiles for the stages of the process compression molding of plates from the granulate of thermoplastic composites: I – initial (a) and final (b) stages of the compression granulate; II – initial (c) and final (d) stages of the melt spinning stage; III – intermediate (e) and final (e) stages of the melt cooling phase; position of the outline: 1 – matrix; 2 – ducts for exhausting air and foraging the melt; 3 – backlash between a plunger and a matrix; 4 – plunger; 5, 6 – granulate before and after compression;

7 – zone of heated granulate; 8 – composite melt; 9 – molded melt; 10 – flash (grat); 11 – glazed part of the melt; 12 – residual part of the melt; 13 – a molded plate

Вследствие температурного расширения часть расплава с остатками воздушных включений при давлении p ( t ) вытекает наружу через зазор 3 и щелевые каналы 2 , образуя облой (грат) 10 , подлежащий удалению при обработке пластины.

Стадия заканчивается в момент t = ( t ₂ + t ₁), отвечающий достижению в плоскости симметрии расплава температуры ( T_p) z = ₀ >  0,97 Т _ф . Величина конечного давления p _к в полости пресс-формы определяется величиной гидродинамического сопротивления каналов 2 и 3 истечению избытка расплава.

На третьей стадии (охлаждения сформованного расплава длительностью t ₃) пресс-форма устанавливается между плитами охладителя и сжимается усилием F _п, верхняя плоскость пуансона принимает при этом температуру T _охл.

В течение времени охлаждения текущая температура плунжера и матрицы пресс-формы изменяется в диапазоне T _охл ≤ T _пф(z, t ) ≤ T _ф. При снижении температуры пресс-формы до температуры стеклования расплава T _cт в момент времени t > ( t ₁ + t ₂) слои, прилегающие к плоскостям матрицы и плунжера, переходят в стеклообразное (рис. 1, д). При этом давление в полости пресс-формы в течение времени охлаждения также непрерывно снижается по некоторому закону p ( t ).

Стадия заканчивается в момент времени t = (t1 + t2 + t3) (рис. 1, е), отвечающий переходу всего объема расплава в стеклообразное состояние и снижению температуры в плоскости симметрии до температуры (T )   ≤ и z=0

1,5 T _охл, исключающей температурную деформацию (коробление) сформованного изделия. Толщина h _и и другие размеры изделия определяются значением линейной усадки, зависящей от разности температурных коэффициентов линейного расширения металла пресс-формы и композита, температур

T _ф и T _и, значений давления формования p _ф и объемного модуля упругости расплава.

При описании первой стадии можно пренебречь нагревом композиции из-за кратковременности процесса. Задачами расчета являются определение: требуемого давления сжатия гранулята р_с ; массы гранулята m _г для формования пластины заданных размеров A и х h и ( A и -площадь изделия (пластины), h _и – его высота); объема полости пресс-формы V _п0 под навеску гранулята; размеров формующей полости с учетом усадки пластины после охлаждения; хода плунжера S ₀.

Стадия протекает при усилии (Н):

F п ≈ 1,2 p 2max S фп , (1)

где p _2max – максимальное давление в формующей полости на второй стадии процесса, Па; S фп – площадь формующей полости, м²; 1,2 – коэффициент запаса по усилию пресса.

В соответствии с полученными экспериментальными результатами для древесно-полимерных композитов различного состава давление, при котором достигается нулевое значение порозности в объеме гранулята, может быть описано с коэффициентом корреляции не ниже 0,98 формулой:

p c = p 0 - kT [МПа], (2)

где T г – начальная температура гранулята, ° С; p 0 - значение давления при T _г = 0; k_T – коэффициент, отражающий влияние температуры на деформируемость гранулята, МПа/ ° С.

Масса гранулята при известных размерах формующей полости пресс-формы может быть вычислена по следующей формуле:

m г = (V фп + V o₆. )[1 — ё , Р ( T ) =

V

ΦΠ

^U 2K ⁽ p 2K , ^T 2K )

Sh

ΦΠ ΦΠ

^U 2K ⁽ p 2K , T 2K )

[кг],

где V _ΦΠ – объем формующей полости (сомкнутой пресс-формы, рис 1, б), м³; V _об – объем облоя, м³; ε ₀ – начальная по-розность гранулята; р (T ) - плотность гранулята, кг/м³; и _2K( p _2K, T_2K) - удельный объем расплава и облоя в конц е второй стадии процесса, м³/кг; p _2K, T _2K – давление (Па) и среднеинтегральная температура ( ° С) расплава в конце второй стадии; h _ΦΠ – высота формующей полости, м.

Удельный объем расплава и облоя, исходя из модифицированного уравнения Ван-дер Ваальса6:

^U 2K⁽ p 2K , ^T 2K )    ^Р

1 R [ 273 + T _2K   T 0

1I p0  M ( p2K + a a

где ц = u ( p = 0, T _r ) - удельный объем композита при температуре T _Γ и отсутствии давления.

Ход плунжера пресс-формы (рис. 1, а–б):

^S 0 = ^h n0 — ^h фо * (⁷)

При известных размерах формуемой пластины при температуре 20 ° С (рис. 1, е) – толщине h_u и площади A _u = l_x × l_y ( l_x – длина по оси x , l_y – длина по оси y ) размеры формующей полости пресс-формы с учетом усадки пластины могут быть определены исходя из деформации массива.

Объемная деформация формуемого изотропного массива исходя из выражения (4) будет равна

где T ₀ = 293 – температура приведения, К; ρ ₀ – плотность композита при температуре T ₀ , кг/м³; R = 8,314 – универсальная газовая постоянная, Дж/(моль К); М (кг/моль), α(Па) – константы уравнения Ван-дер Вальса, подлежащие экспериментальному определению.

Среднеинтегральная температура расплава в конце второй стадии ( ° C):

^U 2 K

3K

3K _

RT 2 K

M ^U 3K^{( a +} Р 2 K )

T 2K = ^ 7 T ( Z , 1 2 ) dz .     (5)

ФП 0

Высота полости пресс-формы под навеску гранулята (рис. 1, а) с учетом его началь н ой среднеинтегральной по-розности ε ₀ при пренебрежении тепловым расширением металла может быть вычислен по следующей формуле:

RT 3K _£ R p 0 Г 273 + T 2 K - 273 + T u

M au„   M a + p a

3k                      2 k

где υ _3K ≅ υ ₀ = 1/ ρ ₀ – удельный объем изделия (пла стины ) в конце третьей стадии, м³/кг; T_3K = T u = T 0 - среднеинтегральная температура изделия в конце третьей стадии, К.

На начальном этапе расчета в первом приближении можно принять:

е »

R p 0 f 273 + Т _ф 273 + T o M ( a + p c      a

=   m ц  =

(1 - ё о) SфП m г

' (1 - ё о ) s Ф_П'

Малые линейные деформации по координатным осям:

^e » ~ ^e x ^{+ e} y ^{+ £} z , £ i = e_v /3 .   ⁽1⁰⁾

Размеры формующей полости пресс-формы в первом приближении:

h ФП = (1 + 8 u /3) h u ;

l ФП x = (1 + 8 u /3) l x ;

l ФП , = (1 + 8 u /3) l c ;          (11)

S ФП = (1 + 8 u /3) ² Ц c ;

VфП= (1 + 8u /3)3 lxlchu , где lФПx, lФПx — размеры формующей полости в плоскости xy, м.

Задачами расчета второй стадии являются определение функций температурного поля T _р ( z, T ), давления расплава p _D( t ) и длительности стадии t ₂, а также уточнение размеров формующей полости по формулам (8–11).

Для принятой расчетной схемы формования пластины, у которой размеры в плоскости xy существенно больше толщины, тепловой поток может быть одномерным. Пренебрегая диссипативными тепловыделениями из-за относительно малых значений скорости нагружения и давления формования, уравнение теплового баланса можно представить в виде следующего нелинейного уравнения, в котором зависимость теплофизических коэффициентов композиции от времени обусловлена изменением как температуры, так и физического состояния (образованием расплава)⁷:

Уравнение (12) не имеет аналитического решения.

Для плоской пластины с постоянным коэффициентом температуропроводности согласно А. В. Лыкову4 при переносе тепла теплопроводностью:

TO

=z

i =1

T

OTH

Т ф - T ( t , z )

Т ф - T _r

p ( T , t ) C p ( T , t )

a t ( z , t ) a t

= — ( A (T , t ) — ) , a z i a z )

где p (T , t ) - плотность среды, кг/м³; c p ( T , t ) - удельная теплоемкость, Дж/(кг∙К); T = f( z,t ) – температура среды, К; Л ( T , t ) - коэффициенты теплопроводности, Вт/(м∙К).

Граничные и начальные условия согласно рис. 1, в–г:

т ( z , t = t i ) = T ;

T p ( z = h n /2, t ) = Т ф= const;       (13)

T p ( z = 0, t = t i + 1 ₂) >  0,97 Т ф .

2 ■ 2 ■ ( - 1) ^{i + 1} (2 i - 1) n

■ cos

exp

(2 i - 1) - I Fo 2 J

KT.

(2 i - 1) ^h ФП .

■ (14)

где Fo = 4 a(T ) t / h ф _п - число Фурье; а ( T ) – коэффициент температуропроводности, м²/с; t – время, с; h _фп/2 – толщина (рис. 1, г) прогреваемого (охлаждаемого) массива гранулята (расплава), м; T ( t, z ) – текущая температура точки массива с координатой z , ° С.

Из анализа, проведенного А. В. Лыковым следует, что выражение (14) представляет собой быстросходящий-ся ряд, причем кривая распределения температуры с погрешностью не выше 1–2 % может быть описана несколькими слагаемыми ряда.

Для расчета коэффициентов температуропроводности использована теория Г. Н. Дульнева³. Было установлено, что для термопластичных древес-но-полимерных композитов на основе полиэтилена коэффициенты температуропроводности a ( T ) сжатого гранулята (композита) и расплава a _p( T ) описываются с коэффициентом корреляции не ниже 0,98 полиномами (15) и (16):

a(T ) = A 3 T ³ + A 2 T ² + A 1 T + A 0 , (15)

a ( T ) = A T ³ + A T ² + A T + A (16) pp3p2p1p0

Из-за температурного расширения избыток расплава из сомкнутой пресс-формы будет вытекать по каналам 3 и 2 из формующей полости наружу,

⁷ Ильюшин А. А. Механика сплошной среды / А. А. Ильюшин. М. : Изд-во МГУ, 1990. 310 с.

538                                   Информатика, вычислительная техника и управление

снижая давление в последней. Для получения функции давления расплава p _D( t ) в формующей полости были приняты следующие допущения:

– гранулят и расплав полностью заполняют формующую полость пресс-формы, в связи с чем воздушные прослойки и градиенты давлений в нем отсутствуют на всем протяжении данной стадии;

– входовыми эффектами при течении расплава в щелевых каналах 3 и 2 можно пренебречь;

– истекают слои расплава, прилегающие к стенке пресс-формы с температурой T _ф и функцией эффективной вязкости, отвечающей уравнению Оствальда:

П ₃ = k o ( Y / а т ) n ^{- 1} = к о a n Y n ^{- 1} , (17)

где k ₀, y , n , T₀, a_T - реологические константы и функции для расплава;

– изменение давления описывается модифицированным уравнением Ван-дер Ваальса 6:

[ p ₂ ( t ) + a ][ u 2 ( T )- b ] = R [273 + T₂ ( t )] / M , (18)

полости и суммарная ширина (в плоскости xy ) каналов 2 (рис. 1, а– б), м; δ ₁ и δ ₂ – высота каналов 3 и 2 , м; h _пл и b _к – длина каналов 3 и 2 , м;

– скорость приращения объема расплава из-за роста температуры в полости пресс-формы определяется выражением:

dV  m _Γ d υ ₂

Q_T == dt dt

V ΦΠ d υ 2 ; υ ₁ dt

– удельный объем композита (сжатого гранулята) после первой стадии:

^U 1 =

- + RR ( T _r- T _o) p ₀ M a

= const ;

– производная по времени удельного объема, исходя из уравнения (18):

d u ₂        R

dt d T( t) d t

—

M [ p ₂( t ) + a ] 273 + T ₂( t ) d p ₂( t )

p ₂ ( t ) + a   d t

где b – константа уравнения, м³/кг;

– среднеинтегральная температура массива будет равна:

^n /2

TAt ) = T" J T ( z , t ) dz ; (19)

ФП 0

– суммарные потери давления (перепад давлений) при истечении избытка расплава через плоскощелевые каналы 2 и 3 :

n n+1      1-n I 1 + 2 n I n p (t ) = 2 k0 aT I I Q "

I ⁿ J (20)

"[П-n d,-(2 n+1) hпл+П-n 5"-2 n+1) bк ], где Q = f(t) – объемная скорость расплава при истечении, м3/с; П и П∑ – соответственно периметр формующей

Из условия сплошности потоков следует, что Q = Q_T . Объединяя выражения (20–23), получаем после преобразований следующее выражение для функции прироста давления к начальному давлению сжатия гранулята p _c :

^d P ⁽ t ) =

[ P ( t ) + a ] -----=--- 273 + T₂ ( t )

d T 2 ( t ) -

[ p ( t ) ]^1/ n [ p ( t ) + a ] d t

1 1/ n l\i n J ^k реол ^k геом ^k сж

где kгеом = (П-n 8;-2n+1)hпл +П-n 8^n+1)bk) -характеристика геометрии пресс-формы; kсж=(Vфп/υ1)nR/M – характеристика сжимаемости формуемой композиции; kреол = 2n+1 k0 aTn [(1 + 2n) / n ]n — характеристика реологического поведения композиции; aT = f(T)=B4 T4 +B3 T3 + + B2 T 2 + B1 T + B0; – функция приведения эффективной вязкости; B0, B1; B2; B3; B4 – коэффициенты полинома.

Длительность t ₂ стадии будет равна:

n

1 2 = S A t i , =1

где Δ t_i – временной шаг решения уравнения (14); n - количество временных шагов, при реализации которых достигается граничное условие T p( z = 0, t = t 1 + 1 ₂) > 0,97 T _o .

Задача расчета третьей стадии – определение ее длительности t ₃.

Для температуры изделия в плоскости симметрии (рис. 1, д–е) при начальном условии T( t ₁ + t ₂ + t ₃, z = 0) ≤ T _охл справедливо выражение:

T =   T ( t , - ) - T w ( t )

OTH.        T 2: - T w ( t )

где Fo = 4 at / H П_Ф - число Фурье; a – среднее значение коэффициента температуропроводности пресс-формы в диапазоне температур 20-160 ° С), м²/с; H _пф – высота (толщина) пресс-формы, м.

Граничные и начальные условия для третьей стадии (рис. 1, д–е):

T(z, t 1 + t 2 ) = T ф ;

T ( z = H _пф/2, t ≥ t ₁ + t ₂) = T _охл = const; (28)

T(z = hфп/2, t ≥ t1 + t2) = Tw(t), где Tф – температура пресс-формы до начала охлаждения, равная температуре формования °С; Tохл - температура верхней плоскости пресс-формы на стадии охлаждения, °С.

Длительность стадии t ₃ будет равна

n

1 3 = £ Д t i ,            (29)

=1

to

=2

i =1

2 • 2 • ( - 1) ' ^{+ 1} (2 i - 1)n

exp

-

(2 i - 1) - I Fo 2 J

• (26)

• cos

_ к z

(2 i - 1) —

ФП .

где T w ( t ) - текущая температура поверхности изделия, равная темпер а туре нижней плоскости плунжера; Т ₂ . -среднеинтегральная температура расплава в конце второй стадии.

Температуру T_w ( t ) = Т _ПФ ( t , z = h _ФП / 2) нижней плоскости плунжера пресс-формы можно определить из уравнения, описывающего распределение температур в пресс-форме на стадии охлаждения:

T

OTH.

T w ( t ) - Т ох л Т ф - Т ох л

to

= 2

i = 1

2 ■ 2 ■ ( - 1) ^{i + 1} (2 i - 1) n

exp

(2 i - 1) - I Fo 2 )

■ (27)

■ cos

(2 i - 1)

^{n h} ФП /2 H ПФ

где Δ t_i – временной шаг решения; n - количество временных шагов, при реализации которых достигается выполнение условия T( t ₁ + t ₂ + t ₃, z = 0) ≤ T _охл.

В связи с тем, что система полученных уравнений не может быть решена аналитически, был разработан численный метод решения, реализованный в программе Simulation Molding Plates9.

Проверка адекватности математической модели и программы расчета была проведена применительно к расчету процесса формования пластины из гранулята полиолефинового компо-зита8 при следующих значениях параметров и характеристик:

• 1)    общие параметры: температура перехода в вязкотекучее состояние Т _вт = 140 С; начальная температура гранулята Т г = 50 С; исходная пороз-ность ε ₀ = 0,464; число сечений по полутолщине сжатого гранулята n _h = 11;

• 2)    геометрические параметры пресс-формы и пластины: δ ₁ = 10^-4 м;

δ 2 = 10^-4 м; b к = 0,025 м; h пл = 0,05 м; H пф = 0,1 м; П = 1,030 м; П ∑ = 0,100 м; l x = 0,3 м; l y = 0,13 м; h и = 0,01 м;

• 3)    теплофизические характеристики композита и пресс-формы ⁹ : A 0 = 1,88∙10^-7; A 1 = 7,12∙10^-10; A 2 = -1,18∙10^-11; A 3 = 0; A р0 = -8, 73∙10^-7; A р1 = 9, 37∙10^-9; A р2 = -1, 91∙10^-11; A р3 = 0; а = 1,22∙10^-7 м²/с ⁹;

• 4)    реологические характеристики : B 0 = 412,10; B 1 = -8,97; B 2 = 7,23∙10^-2; B 3 = -2,61∙10^-4; B 4 = 3,52∙10^-7; k 0 = 312238 Па∙сⁿ; n = 0.25; Т 0p = 150 С; M = 0,0169 кг/моль; α = 432∙10⁶ Па; ρ ₀ = 1163 кг/м³; Т ₀ = 293 К.

• 5)    стадии нагрева и охлаждения: Т ф = 150 С, Т охл = 20 С.

• 6)    рассчитанные параметры: масса пластины m п = 0,378 кг; масса гранулята m г = 0,382 кг; p 2c = 3,3 МПа; t 2 = 480 с; t 3 = 230 с; F п = 845 кН; h фп = 10,56 мм; h п0 = 17,7 мм; l фп х = 316,8 мм; l фп y = 137,3 мм.

В соответствии с методикой эксперимента плиты пресса и пресс-форма были нагреты до температуры 150 ° С. Далее в пресс-форму была установлена предварительно сформованная пластина из полиолефинового композита.

В горизонтальной плоскости симметрии вдоль ширины пластины было просверлено отверстие диаметром 3 мм, длиной 65 мм. Соосно ему в матрице пресс-формы было выполнено такое же отверстие. В них был размещен датчик электронного термометра ЛТИ-Н (погрешность измерения ±(0,3+0,005 T )). В течение времени нагрева и охлаждения пресс-формы секундомером измерялось время и фиксировалась температура в центре пластины.

Полученные экспериментальная и расчетная кривые изменения температур массива и пресс-формы представлены на рис. 2.

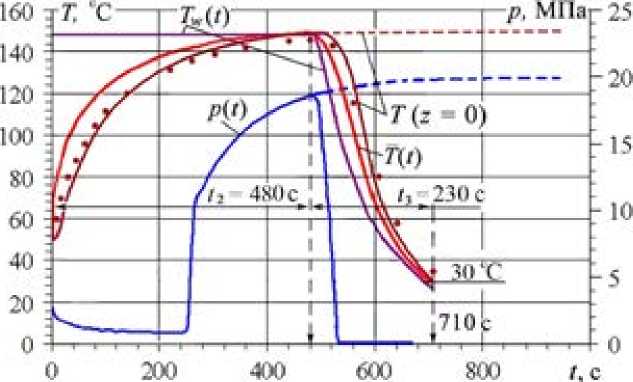
Р и с. 2. Изменение значений температур T ( t ) и давления p ( t ) в полости пресс-формы в тече н ие второй ( t ₂) и третьей ( t 3 ) стадий формования массива: T ( z = 0) - температура в плоскости симметрии; T ( t ) - среднеинтегральное значение температуры; T _w ( t ) – температура поверхности плунжера; точки – экспериментальные значения температуры в плоскости симметрии; пунктирные линии – изменение температуры T ( z = 0)

и давления p ( t ) при увеличении длительности первой стадии

F i g. 2. Change of temperature values T ( t ) and pressure p ( t ) in the mold cavity during second ( t2 ) and third ( t3 ) stages of forming the array: T ( z = 0) – temperature in the plane of symmetry; – mean integral temperature; Tw ( t ) – surface temperature of the plunger; the points are the experimental values of the temperature in the plane of symmetry; the dotted lines are the temperature change T ( z = 0) and pressure p ( t ) with increasing duration of first stage

Из графиков следует, что максимальное расхождение экспериментальной и теоретической кривых (до 15 %) имеет место на начальном и конечном участках кривой, что связано с быстрым изменением температуры и запаздыванием ее регистрации из-за инерционности прибора. В области выхода температур на стационарные значения (200–500 с) разница экспериментальных и расчетных значений не превышает 3 %. Коэффициент корреляции Пирсона R ², рассчитанный в программе MS Ecxel, составляет 0,976, что свидетельствует об адекватности математической модели и программы расчета.

Из кривой p ( t ) (рис. 2) следует, что скорость изменения давления на стадии нагрева, начиная от момента времени ~ 70 c (отвечающего началу плавления поверхностного слоя композиции), отстает от скорости изменения температуры, а на стадии охлаждения наоборот опережает. Это объясняется уменьшением объема расплава в полости из-за истечения его избытка (4 г) в облой. Общая длительность процесса формования составляет 710 с.

Обсуждение и заключения

Прикладная технико-экономическая значимость разработанной ма-

Том 27, № 4. 2017

тематической модели и программы расчета Simulation Molding Plates5 для российского и зарубежного сообщества заключается в том, что она позволяет адекватно моделировать процессы компрессионного формования тонкостенных изделий в виде пластин и фрагментов оболочек, что обеспечивает сокращение финансовых и трудовых затрат предприятий при освоении производства новых и улучшении качества серийных изделий.

Полученные результаты позволяют на стадии проектирования технологического процесса при известных значениях реологических и теплофизических характеристик формуемой композиции рассчитать и оптимизировать основные факторы, определяющие качество изделий: геометрические размеры формующей полости пресс-формы, обеспечивающие требуемые размеры изделия с учетом термической и компрессионной составляющих усадки композиции; общую длительность цикла формования; требуемое усилие пресса на трех стадиях процесса; его производительность при заданных значениях температур формования и охлаждения; величину технологических потерь, обусловленных истечением расплава в облой и др.

542                                   Информатика, вычислительная техника и управление

Поступила 07.09.2017; принята к публикации 30.10.2017; опубликована онлайн 19.12.2017

Все авторы прочитали и одобрили окончательный вариант рукописи.

Submitted 07.09.2017; revised 30.10.2017; published online 19.12.2017

All authors have read and approved the final version of the manuscript.