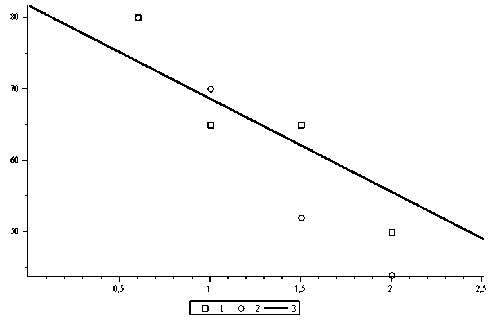Математическая модель несущего слоя газожидкостного подшипника скольжения

В Красноярском государственном техническом университете разработаны конструкции радиальных комбинированных подшипников, у которых рабочий зазор состоит из несущего газового слоя и слоев смазки (А. с. 1042400СССР, МКИF 16C 17 16. Комбинированныйпод-шипник / А. С. Тюриков, С. Н. Шатохин, В. М. Грук. № 2586690; заявл. 3.09.78.). Эти конструкции отличаются повышенной несущей способностью, пониженной вибрационной активностью, надежностью в работе и долговечностью. Такие подшипники применяются в целях улучшения качества и условий эксплуатации оборудования, например для вентиляции отсеков надводных и подводных кораблей, что позволяет значительно снизить шум и вибрацию.

Математическая постановка задачи. При построении математической модели несущего газового слоя жидкостного подшипника делается предположение о постоянстве плотности и вязкости газа и выполнении уравнения состояния

P

— = const,                 (1)

p гдеP-давление; p -плотность.

С учетом малости относительной толщины смазочного пространства получены соответствующие уравнения Рей- нольдса для давления, являющиеся основополагающими для расчета основных характеристик таких подшипников [1; 2].

Рассмотрим бесконечный двухслойный ( i = 1 , 2) цилиндрический подшипник. Центр шипа радиуса R ₁ в точке O ₁ , центр втулки радиуса R ₂ в O ₂ . Пусть шип и втулка вращаются с угловыми скоростями ® 1 и ю ₂ соответственно. Первая среда ( i = 1) - газ примыкает к шипу, вторая ( i = 2) - жидкость - к втулке (рис. 1). Движение можно считать плоским между двумя эксцентрично расположенными окружностями. Рассматривается установившееся течение.

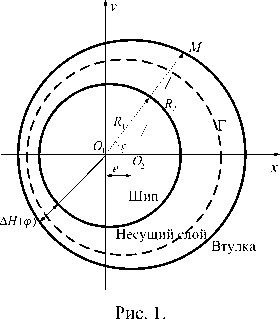
Двухслойный поток в смазочном слое представляет собой совместное движение двух несмешивающихся сред – жидкости и газа, контактирующих по некоторой линии (линии раздела) Γ .

Для каждого слоя запишем уравнения Навье–Стокса

ρ _i

dV ( i ) dt

- grad P ^{( i )} +

+ц _t А V (¹) + ^Ц- + ц ' J grad div V (¹) и неразрывности

div ( ρ i V ^{( i )} ) = 0 , (3)

где V ^{( i )} – вектор относительной скорости движения частицы жидкости; _P ^{( i )} – давление; μ _i – коэффициентвяз-кости; ρ _i – плотности сред; μ _i ^′ – второй коэффициент вязкости. Для жидкого слоя последнее слагаемое в (2) от-

ц у > d V d P (    ‘ P = 0

P a R 1 ∂ζ ²      ∂ϕ , ∂ζ ,

^d ( ^p i V ri ) ) ^d ( ^p i V Ф ) ) _n += 0 .

∂ζ ∂ϕ

Рассмотрим граничные условия.

Условие на шипе ( ζ = 0 ) :

V ⁽¹⁾    « R у ⁽¹⁾ ₌₀

V _ϕ =, V_r = 0.

V ₀

Условие на втулке ( ζ = H ₀ ( ϕ ) ) :

V (2) = ^Ю 2 R 2    V (2) = V (2) dH 0

^ϕ V ₀ ^{, r ϕ} d ϕ ^.

Условие на линии раздела ( ζ = ζ _а ) :

JZ (1)₌ F (2)₌ F F (i) ₌ у ( i ) ^dZ a

V _ϕ V _ϕ V _a , V_r   V _ϕ

сутствует.

При постановке граничных условий будем следовать работам [3; 4].

Рассмотрим третье условие в (5). Запишем тензор

напряжений

На поверхности шипа и втулки – условие прилипания:

I

V

I

V шипа ,

I

V

I

⁼ V втулки .

_P ( i ) ₌ 2 μ _{i E} ( i ) _+(- P ( i )

( i ) λ′ div V ) I .

На линии раздела Γ : F ( x , y ) = 0 :

V (1) = V (2) , V <0 . $ F = 0,

P ⁽¹⁾ - n - P ⁽²⁾ - n = 2 о H I + V_rG,          (5)

где P ^{( i )} – тензор напряжений в i -м слое; H – средняя кривизна поверхности раздела сред; и - единичный вектор нормали к линии Γ , направленный во вторую область; V_r = V- n ( и -V ) -векторныйдифференциальный оператор (поверхностный градиент); ^σ – коэффициент поверхностного натяжения.

К каждому слою в полярной системе координат с центром в O ₁ (центр шипа) запишем систему уравнений, которая получается из (2) и (3) после линеаризации по малому параметру ^h , h = R ₂ - R ₁, характерному для R ₁

подшипников скольжения [1; 2]:

_∂ 2 V _ϕ ( i ) 1 _∂ P ( i )     _∂ P ( i ) 0

^{μ i} ∂ r ^{2 =} r ∂ϕ ^, ∂ r ^=, _{∂(ρ iVr} ( i ) _{) 1 ∂ ( ρ iV ϕ} ( i ) ₎ + = 0 .

∂ rr ∂ϕ

Перейдем отпеременной r к переменной ζ : r = R 1 + h ζ, 0 ≤ζ≤ H 0 ( ϕ ) , e

H ( ϕ ) = 1 +ε cos ϕ , ε= , h = R - R . 0 h     21

Уравнение линии раздела запишем в r = R ₁ + h ζ _a( ϕ ) .

Перейдем к безразмерным величинам: _{V ϕ} ( i ) _{= V 0 V ϕ} ( i ) _{, Vr} ( i ) _{= V 0} h_Vr ( i ) _{=ω 0 hVr} ( i ) _, R ₁

р(') = pa R^р<0, p(i) =pap, h где V0=ω0R1; ω0=ω1+ω2; Pa – атмосферное давление; ρa – плотность в состоянии покоя. С учетом мало-

Для жидкого слоя последнее слагаемое в (10) равно нулю, таккак div V = 0. Для газового слоя X' = —3 ^ , E ⁽ ' ) -тензоры скоростей деформации; I – единичный тензор. С учетом малости ^h

R ₁

_P ( i ) ₌

-

_P ⎛ R 1 ⎞ ^{2 a}

⎝ h ⎠

%*

Ц ' ® 0 R i ^d V ' ) h ∂ζ

виде

сти ^h перепишем уравнения (6) в безразмерных вели-

R ₁

чинах:

ц _г ® 0 R 1 ^d ^%^ )

-

h

2 ct Hn + V_rG =

P ^{⎛ R 1} a ⎜_{⎝ h} 2 σ ⎞ _{R 1} ⎟_⎟

1 ∂σ ⎟ r ∂ϕ ⎠

∂ζ

%*

получаем на линии раздела

8 Z ⁽¹⁾      ак⁽²⁾

p z (1) = P (2), ц _ _ Ф_ = ^₂^d V L_ ¹∂ζ ²∂ζ

.

,

Таким образом, приходим к следующей задаче: требуется найти функции ^(^(Z,^), V^’CZ,^), P°')(Z,V) и уравнение линии раздела ζ = ζa (ϕ) из уравнений d2 V(i)     1 dIs(i) dF>(i) 0

∂ζ ^{2 =} k ∂ϕ ^, ∂ζ ^=,

r               ϕ

+= 0, ⎜ k =

∂ζ ∂ϕ ⎝ P при следующих граничных условиях.

На шипе ( ζ = 0 ) :

V (i)i     =^ i R i      « 1

^{ϕ ζ= 0}    V ₀ ω ₁ +ω ₂ ^,

V Z ⁽¹⁾| = 0 , ^r ζ= 0

На втулке ( ζ= H ₀ ) :

1    _∂ P % (2)

% (2)

V ^ϕ  ζ= H 0

ω₂ R ₂      ω₂

V ₀ω₁+ω₂

,   V ^% r ⁽²⁾ [

ζ= H 0

ω∂ H

20,(13) ω1+ω2∂ϕ

-

12 k ₂ ∂ϕ

На линии раздела ( ζ = ζ _a ) :

3 ω ₂ ( H ₀ -ζ _a ) ^{( H 0 -ζ a )+} 2 ( ω 1 +ω 2 ) V ^% a ( H 0 -ζ a) _r

% (1)

^{V ϕ} ζ=ζ a

% (2)              %       % ( i )

^{V ϕ}   ζ=ζ a ^{V a , Vr}  ζ=ζ a

_{= V} % ( i ) ∂ζ a ϕ _∂ϕ

, (14) ζ=ζ a

Далее удовлетворяем второму условию (15), учитывая (16, 17):

_P % (1)       _{= P} % (2)      _,

ζ=ζ a          ζ=ζ a

∂ V ϕ ⁽¹⁾ μ 1 _∂ζ

ζ=ζ a

₌   ∂ V ϕ ⁽²⁾

μ 2 _∂ζ

ζ=ζ a

. (15)

_⎛ 1 _∂ P % (1) ^{μ 1 ⎜} _⎝ 2 k ₁ ∂ϕ ^{ζ a}

ω ₁

-

—

V a

ζ _a ( ω ₁ +ω ₂ ) ζ _a

-

Здесь V _a–неизвестнаябезразмернаяскорость.

С учетом, что P ^{( i )} независитот ζ (11), первое уравнение в (11) является обыкновенным дифференциальным уравнением по ζ . Можно выписать его решение, удовлетворяющее условиям (12), (13) и (14):

=μ ₂

_% (2)

1 ∂ P _{( H 0 -ζ a )+}

2 k ₂ ∂ϕ

ω ₂

—

V a

.

( H ₀ -ζ _a )( ω ₁ +ω ₂ ) H ₀ -ζ _a ^⎟ _⎠

V % ⁽¹⁾ = ^{1 ∂ P (1)} ζ ( ζ-ζ ) + ^{ω 1 ( ζ a -ζ )} + ^{V a ζ} ,

^ϕ     2 k 1 ∂ϕ ^a     ζ a ( ω 1 +ω 2 ) ζ a ^,

ϕ

% (2)

1 ^{∂ P} ( H 0 -ζ )( ζ a -ζ ) +

2 k ₂ ∂ϕ

Так как P ⁽¹⁾ и P ^{% (2)}зависяттолькоот ϕ и на линии раздела совпадают, то функцию давления можно искать в виде одной функции P (ϕ), не зависящей отномера среды. В уравнениях (20)–(22) проведем следующие замены:

P ^{% (1)} = P ^{% (2)} = P ^% = ^{h 2}2 P ,ζ a =δ H 0 , V ^% a = V a ,

R ₁

ω 2 ( ζ-ζ a )

V a ( H 0 -ζ )

( ω ₁ +ω ₂ )( H ₀ -ζ _a ) H ₀ -ζ _a

.

ω R     6 μ RV

V ₀ = ( ω ₁ +ω ₂ ) R ₁ , Ω _i = ⁱⁱ , γ _i = ^{i 1} ₂ ⁰

V ₀ P_ah ²

.

Далее интегрируем уравнение неразрывности, тре-тьев(11), по ζ от0до ζ _aиот ζ _aдо H ₀. Получаем

Система уравнений (20), (21), (22) с учетом уравнения состояния (1) примет следующий вид:

ζ a _{∂(ρ % 1 V} % _r (1) ₎ ζ a _{∂(ρ % 1 V} % _ϕ (1) ₎

0 ∂ζ

∂ϕ

d ζ=

= V ^% r ⁽¹⁾ ρ % 1 _ζ=ζ - V ^% r ⁽¹⁾ ρ % 1 ^{r 1} ζ=ζ a ^{r 1} ζ= 0

-

V % (1) ρ _% I ∂ζ _{a +} ^{ϕ 1} ζ=ζ a _∂ϕ

dP ( ϕ ) d ϕ

⎛

×^⎜ V a ( ϕ ) +Ω 1

γ 1        _×

δ ² ( ϕ ) H 0² ( ϕ )

_{+      1} 1                   ⎟_,

P ^κ ( ϕ ) δ ( ϕ ) H 0 ( ϕ ) ^⎟⎠

ζ _a

+^∂ V % ⁽ ϕ ¹⁾ ρ % 1 d ζ= 0 .

∂ϕ ₀

С учетом (12–14)

dP ( ϕ )

γ ₂

d ϕ     ( 1 -δ ( ϕ ) ) ² H 0² ( ϕ )

×

ζ _a

^∂ V ^% ϕ ⁽¹⁾ ρ % 1 d ζ = 0;

∂ϕ ₀

ζ a

∫ V ^% _ϕ ⁽¹⁾ ρ %₁ d ζ= const .      (18)

×⎜ V _a( ϕ ) + Ω ₂ +

(1 -δ ( ϕ )) H 0 ( ϕ ) ^⎟⎠

И аналогично (после интегрирования от ζ _aдо H ₀) получаем

3 dP ( ϕ ) d ϕ

γ ₁

δ ( ϕ ) H 0² ( ϕ )

( Ω 1 - V a ( ϕ ) ) +

_V % (2)

^r   ζ= H 0

-

_V % _r (2)      _{+ V} % _ϕ(2) I X

V_r    + V _ϕ ×

+

γ ₂

×^{∂ζ a} - V ^{% (2)} ∂ϕ ^ϕ

⋅^{∂ H 0} +^{∂ H 0} V % ⁽²⁾ d ζ= 0 ^{ζ= H} 0 ∂ϕ ∂ϕ ^ϕ ζ _a

( 1 -δ ( ϕ ) ) H 0² ( ϕ )

( Ω 2 - V a ( ϕ ) ) .

исучетом(13), (14) ипостоянстваплотностивовторомслое

H ₀ H ₀

^∂ V ^% ϕ ⁽²⁾ d ζ=0;     V ^% ϕ ⁽²⁾ d ζ =const.

∂ϕ

ζ _a ζ _a

Подставляем найденные выражения для V _ϕ ⁽¹⁾ (18), (19) и после интегрирования получаем

1 ∂ P ^{% (1)}        ωζ      V ^% ζ    C

-ζ ³ + ^1a + ^aa = ¹

12 k ₁ ∂ϕ ^a 2 ( ω ₁ +ω ₂ ) 2      ρ %₁ ^,

и

_{V ϕ} (2) _в

Здесь C ₁и C ₂поканеизвестныепостоянные.

Уравнение (23) является аналогом уравнения Рейнольдса для газового подшипника, у которого газовый слой находится между шипом и линией раздела (от0до δ ( ϕ ) H ₀( ϕ )). Уравнение(24) являетсяуравнениемРей-нольдса для жидкостного подшипника, у которого жидкостный слой расположен между линией раздела и втулкой (от δ ( ϕ ) H ₀( ϕ )до H ₀( ϕ )). Уравнение(25) характеризуе т поле скоростей и тензоры напряжений при переходе через неизвестную границу раздела сред.

Выведем дополнительные условия. Первое условие – периодичность давления

P ( ϕ + 2 π ) = P ( ϕ ) .

Для получения других условий можно считать, что масса газа и жидкости, содержащихся в смазочном слое,

остается постоянной. В случае газового слоя масса его равна массе покоя, если давление в газовом слое можно считать постоянным и равным атмосферному давлению P _a , что характерно для полноохватывающих подшипников бесконечной длины, когда смазочный слой полностью изолирован от внешней среды [1].

Пусть m_i – масса i -го слоя, M_i – масса смазочного слоя полностью заполненного i -й средой. Найдем массу газового слоя m ₁ с учетом уравнения состояния (1) и массу газа M ₁ для случая газового подшипника в состоянии покоя:

2 π 2 π ∫ P δ H ₀ d ϕ = ∫ P δ ( 1 00

∞

+ε cos ϕ ) d ϕ= ∑ b_n ε ⁿ = n = 0

= 2 π k , b ₀ = 2 π k , b_n = 0 , при n ≥ 1 . (31)

Найдем нулевое и первое приближения решения. В нулевом приближении система (23)–(25) и дополнительные условия (26)–(28) примутследующий вид (достаточно в системе положить ε= 0):

dP ₀    γ ₁ ⎛            C ₁₀ ⎞

=V++, dϕ    δ02 ⎜⎝a0 1 P0δ0 ⎟⎠ m1

2 _π      R ₁ + h ζ _a            2 _π      R ₁ + h ζ _{a                 κ}

= ∫ d ϕ ∫ ρ rdr = ∫ d ϕ ∫ ⎜ ^{a ϕ} ⎟ rdr ≈ 0 R ₁0 R ₁ ⎝ C ⎠

_κ 2 π ₁

≈ hR 1 ^⎛⎜ ^{P a ⎞}⎟ P ^κ ( ϕ ) ζ a ( ϕ ) d ϕ ,

⎝ C ⎠ 0

M =π R ² - R ² ρ ≈ 2 π R h ρ . 121a1a

P 0

dP     γ              с dP0      γ2                 C20

d ϕ⁼ ( 1 -δ ₀ ) ² ⎜ _⎝ ^{V a0 +Ω 2 +} ( 1 -δ 0 ) ⎟ _⎠ ^,

3 ⁰ = γ ¹ ( Ω ₁ - V _a0 ) +γ ² ( Ω ₂ - V _a0 ) , d ϕδ ₀ ( 1 -δ ₀ )

2 π 2 π

( ϕ+ 2 π ) = P ₀( ϕ ) , ∫ δ ₀ d ϕ = ∫ P ₀ δ ₀ d ϕ = 2 π k .

⎛ P a ⎞ ^κ

Учитывая, что ρa =⎜    ⎟ (из уравнения состояния), получаем           ⎝C ⎠

Нулевое приближение, при ε= 0, соответствует те-

чению между двумя концентрическими окружностями. Исходя из симметрии заключаем, что δ ₀ , V _a0 не зависят от ϕ . Тогда (с учетом периодичности)

m ₁

M 1

1 2 π

κ 1 hR 1 ^⎛⎜ ^{P a ⎞}⎟ P ^κ ( ϕ ) ζ a d ϕ

C

2 π R h ρ 1a

2 π ₁ ∫ P ^κ ( ϕ ) ζ _a d ϕ 0

2 π

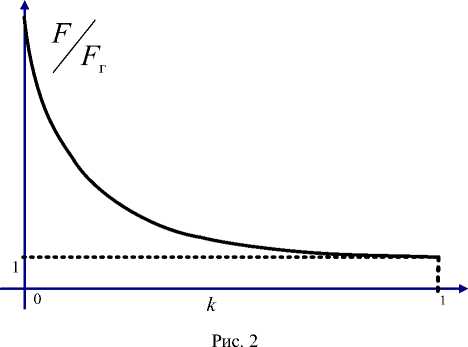
=ρaS1=S1 =k(0

2π₁2π₁

∫ P^κ(ϕ)ζ_a(ϕ)dϕ = ∫P^κ(ϕ)δ(ϕ)H₀(ϕ)dϕ=2πk.(27) 00

Поступая аналогично для жидкостного слоя, получаем 2π2π ∫ζ_a(ϕ)dϕ=∫δ(ϕ)H₀(ϕ)dϕ=2πk.      (28)

Таким образом, приходим к следующей задаче. Требуется найти решение системы уравнений (23)–(25) относительно трех неизвестных функций P(ϕ), V_a (ϕ),δ(ϕ)идвух констант C₁ и C₂ , при дополнительных условиях (26)–(28).

Решение задачи разложением в ряды по относительному эксцентриситету. Рассматривается система (23)–(28). Слабое влияние температуры на вязкость газов дает возможность считать, что процесс, протекающий в смазочном пространстве подшипника, изотермический ( κ =1).

В предположении малого относительного эксцентри- ситета ε решения ищем в виде степенных рядов по ε : ∞∞

δ(ϕ)=∑εnδn(ϕ),P(ϕ)=∑εnPn(ϕ), n=0                       n=0

∞∞∞ Va(ϕ)=∑εⁿVan(ϕ),C1=∑εⁿC1n, C2=∑εⁿC2n.(29) n=0n=0n=0

Запишем дополнительные условия на δ_n (ϕ), P_n (ϕ), Van (ϕ), C1n , C2n.

Pn(ϕ)=Pn(ϕ+2π), 2π2π

∫ δH0dϕ =∫δ(1+εcosϕ)dϕ=∑ anεn = 00

= 2πk, a0 = 2πk, an =0, при n≥1, dP0 =P= m, =C3,P0=C3ϕ+C4, dϕ

C₃=0, P₀=C₄, P₀не зависитот ϕ.

Далее из (30), (31) следует, что δ₀=k, P₀=1.

Находим V_a0, C₁₀, C₂₀ . Подставляем найденные δ₀=k и P₀= 1 в систему (32, 33). Получаем систему трех линейных уравнений относительно V_a0,C₁₀,C₂₀ , из которой

V_a0=²,C₁₀=-k¹, C₂₀=-(1 -k)²,   (35)

AAA

A= γ₁(1-k) +γ₂k,A₂=γ₁Ω₁(1-k) + γ₂kΩ₂,

B₁=2γ₁Ω₁(1-k)+γ₂k,B₂=2γ₂Ω₂k+γ₁(1-k).

Учитывая нулевое приближение, получаем систему для нахождения первых приближений dP1(ϕ) = γ1× dϕ    k2

×⎛Va1(ϕ) + C11 +B1 P(ϕ)1 + B1 δ1(ϕ) + B1 cosϕ⎞, (36) ⎝a kA kA A ⎠ dP1(ϕ)=γ2× dϕ    (1-k)2

× V (ϕ)+C21 -B2   δ(ϕ)+ B2 cosϕ ,

⎜⎝a1      1-kA(1-k)1 A dP1(ϕ)    γ1δ1(ϕ)⎛γ1Ω1(1-k)+γ2kΩ2⎞

3       =-       ⎜Ω1 -⎟+ dϕ        k2 ⎝A⎠

γ₂δ₁(ϕ)⎛γ₁Ω₁(1-k)+γ₂kΩ₂⎞

+(1-k)2⎜⎝Ω2-          A ⎟⎠-

_-γ₁V_a1(ϕ)_-γ₂V_a1(ϕ)k1-k,

P1(ϕ)=P1(ϕ+2π),²∫^πδ1(ϕ)dϕ=0,²∫^πP1(ϕ)dϕ=0.(39)

Полученоявноереш0ение системы 0

^al(V) =

51(Ф) =

где

^р(ф) ^—      , (^sinФ^-Qcos ф)^,

Q²+1

C„ = 0, C21 = 0,

Y2 (Q² +1)(E(1 -k)-AB2) EB2 (1 - k) cos ф

^^^^^в

A (E (1 - k)-AB₂)’

AR (1 - k)2 (3ky₂ + A(1 - k))(sinф- Qcosф)

Y2 (Q² +1)( E (1 - k)-AB2) AB2 (1 - k) cos ф

^^^^^в

E(1 -k)-AB2 ,

E = YiY2 (Q2-Qi), Q —

-

Y1B1    R —_P aAk2 ’         a’

a — -1 +--7—7----7------7—2--+

Y₂(E(1 -k)-B₂A)k²

Y1 B1 (1 - k )2 (3ky₂+ A (1 - k))

Y₂(E(1 -k)-B₂A)k³    ’

Y1EB2 (1 - k)

^P    A(E(1 -k)-AB2)k²

Y1B1B2 (1^-k)      Y1B1

-

(E(1 -k)-AB2)k³ Ak²'

Таким образом, в линейном приближении

5(ф) ~ 8₀+ 851 (ф), Va (ф) ~ Va0 + ^SVa1 (ф), P(ф) ~ P0 + 8Р1(ф), C1 ~ C10, C2 ~ C20.

Используем найденные формулы распределения давления для определения интегральных характеристик газожидкостного подшипника.

Для проекций главного вектора сил давления на линию центров и направление, ей перпендикулярное, после интегрирования получаем

FX = ^-R1 ^Pa J ^P cos фdф = ^Pa QR+Q

2?               R 8R

^Fy = ^{- R}1 ^Pa J ^P sin фdф = ^{- P}a 73— 0                ^{Q + 1}

п,

п.

Тогда удельная нагрузка определится формулой

S —

F + F = 1 8R п

2 Pa R1      2 _xQ . 1

.

Полагая в выражениях для R и Q (45) k — 1, что соответствует чисто газовому подшипнику, получим известную формулу для удельной нагрузки газового подшипника [1]

_{S —}F_—1 ⁸Y1ⁿ

2 Pa R1  2 ^Yf+i.

Для удельных моментов трения S_mi на шипе и втулке также получены явные формулы:

S , —       t(1) dф — x m1    7 p J to

2P_a0         2P_a

2п

X J Ц1®0

RL dV%f h az

d ф —

z—0

2п

S

Ц1®0 ^R1 ^{( V}a0  ^Q1 )

2п

’   —       T<2) dф — m2                 to

2P

Phk a

X

2P

п,

2п

^XJ Ц2®0

R1 dV7 h dZ

^2^to0^R1 ^(Q2 ^Va0 ) d ф —--------;-----;----п.

Ph (1 - k)

Z—H 0              ^{a v 7}

Отношение подъемной силы комбинированного подшипника F к подъемной силе газового подшипника F_г в зависимости от k при следующих значениях: to1 — 260 c^-1, to₂— 0 c^-1(втулка неподвижна), R1 — 3,492 6 см, R₂ — 3,502 8 см, h — R2 - R1 —102 мкм , Ц1 — 1,9 • 10^-10кгс • см^-2• c, Ц₂— 1,02 ■ 10 ³кгс ■ см²■ c показано на рис. 2. При любом 0 < k< 1 отношение подъемных сил больше единицы, причем при увеличении k оно уменьшается и стремится к единице. Это связано с увеличением доли газа и уменьшением доли жидкой смазки в смазочном пространстве.

Зависимость толщины несущего газового смазочного слоя газожидкостного подшипника от подъемной силы при тех же значениях параметров, что и на рис. 2, и k — 0,8 показана на рис. 3. Экспериментальные данные представлены точками, теоретические – прямой линией.

Рис. 3

Таким образом, нами построена математическая модель газожидкостного подшипника, обобщающая модели отдельно жидкостного и отдельно газового подшипника. В линейном приближении по относительному эксцентриситету получено решение задачи и выведены формулы основных числовых характеристик (удельной нагрузки, удельных моментов трения на шипе и втулке). Проведено сравнение полученных числовых характеристик рассматриваемой модели с экспериментальными данными действующего газожидкостного подшипника. Результаты показали достаточную их близость как в количественном, такив качественном отношении.