Математическая модель обобщенного теплообмена в топке котельного агрегата - парадигма теплообмена

Совершенствованию характеристик котельного оборудования мировая энергетика уделяет постоянное внимание, выделяя значительные средства для повышения качества материалов и разработки методов расчета и проектирования котельных агрегатов (КА), так как эти вопросы тесно связаны с экономическими и экологическими показателями работы электростанций. Эта тенденция отражена в международной программе THERMIE-II и работах ведущей фирмы Alstom [1], где основные теоретические направления – это усовершенствование конструкций КА с помощью комплекса программ ANSYS и улучшение свойств термостойких материалов [2]. В РФ приняты нормативные методики расчета КА [3], разработанные В.Н. Тимофеевым (ВТИ) с учетом работ А.М. Гур-вича (ЦКТИ) и С.Н. Шорина (ЭНИН); за более чем полувековую практику применения нормалей они неоднократно уточнялись и усовершенствовались на основе обширной экспериментальной и производственной практики.

В области численного моделирования процессов в КА в РФ известны работы Томского политехнического университета [4] под названием FIRE 3D, а также работы, выполненные в Казахстане и Новосибирске в отношении Hi-Tech проектирования [5]. Однако при использовании мощных вычислительных средств в решении этих задач можно столкнуться со значительными трудностя- ми, связанными со сложностью математической формулировки реальных явлений. В этом случае рационально использование методов системного анализа, позволяющего производить декомпозицию сложной математической модели на более простые части, сформулировать математическое описание в конкретных условиях, установить связь между отдельными частями сложной системы, а затем синтезировать частные решения в направлении полного решения задачи [6–10]. Ниже излагается этот метод в применении к разработке математической модели основного объема топки КА.

• 1.    Формулировка задачи и получение дифференциального уравнения температурного поля в топке

Закон сохранения энергии в виде баланса тепловых потоков для объема топочной среды V в канале топки котельного агрегата для условий стационарного во времени теплового режима можно записать в виде divqK + divqT + div(jл = 0.                     (1)

В этом уравнении: q _к = u p с_рТ _об - вектор конвективного переноса энтальпии топочной среды, Вт/м²; q _T = -X _t V Т _об - вектор диффузионного переноса энергии теплопроводными турбулентным и молекулярным механизмами, Вт/м²; _л =-Х_л V Т _об -вектор диффузионного лучевого (радиационного)

переноса энергии топочной среды, Вт/м². Коэффициентами теплопроводного и лучевого переноса являются λ_т = λ_мол + λ_турб, Вт/м·К, и λ_л = 16σ₀ Т ³/3 k _ср, Вт/м·К, где σ₀ = 5,67·10^–8, Вт/м²·К⁴ – коэффициент излучения абсолютно черного тела, k _ср – средний по объему топочной среды коэффициент ослабления, 1/м. Перенос теплоты также возможен совместно с переносом массы вещества в условиях температурного градиента V Т об с коэффициентом переноса D ρ c_p ≡ λ_м, Вт/м·К, при этом плотность теплового потока составит _м =-X_MV Т об , Вт/м², D – коэффициент массовой диффузии, м²/с. Это позволяет все диффузионные механизмы объединить с помощью равенства λ об = λ мол + λ турб + + Х_л + А м , тогда об = —А об V Т _об.

Первое слагаемое уравнения (1) характеризует дисперсионный механизм прихода энергии в объем V , два других относятся к диссипативным механизмам, связанным с потерями энергии, что и отражено знаками минус. Поступление энергии в основной объем топки с конвективным потоком из зоны интенсивного горения (ЗИГ) идет с температурой Т _н, скоростью w_x и степенью химического недожога ξ . Начальная температура связана с коэффициентом сохранения теплоты в ЗИГ φ_ЗИГ и может быть определена по зависимости Т _н = φ_ЗИГ Т _ад, где Т _ад – адиабатическая температура горения, определяемая по теплоте сгорания топлива и дополнительному внешнему поступлению теплоты с компонентами горения. Коэффициент φ ЗИГ определяется расчетом теплообмена в ЗИГ согласно [7]; степень химического недожога ξ можно определить по методике [8].

Таким образом, с учетом принятых уточнений уравнение энергии (1) преобразуется к виду рср WVТоб - div(Хоб VТоб + рсрDVТоб) = 0. (2)

Далее, при делении на р с_р , замене w на w x и введении относительной температуры θ = Т _об – Т _ст, где Т _ст – температура тепловоспринимающих поверхностей в этой части топки КА, возможен переход к каноническому виду дифференциального уравнения

529  wx 59 529

- ---+

5 х ² а _об 5 х 5 у¹¹

В уравнении (3) а _об ≡ λ_об/ρ с_р – обобщенный коэффициент температуропроводности, м²/с. Кроме того, принято, что изменение температуры вдоль координаты у связано только с градиентнодиссипативным вторым слагаемым в (2), а изменение Т об вдоль координаты х связано только с конвективно-дисперсионным первым слагаемым в (2).

Изложенная выше методика формирования уравнения энергии допускает расширенное применение в виде включения других источников или стоков энергии в потоке топочной среды. Главным критерием отнесения дополнительных ис- точников к конвективно-дисперсионной или к градиентно-диссипативной части уравнения (2) является не знак источника (плюс или минус), а форма его участия в уравнении (2) – с grad Tоб или с div grad Tоб. Аддитивная форма уравнения энергии также позволяет учесть подачу потока газов рециркуляции путем разделения всей длины канала топки на участки, причем выходные из первого участка параметры являются входными для второго с учетом материального и теплового баланса места ввода.

Решение полученного уравнения энергии методом Фурье

В допущении принципа мультипликативного представления искомой температурной функции θ = θ _х ·θ _у можно применить метод разделения переменных, что приводит к системе из двух линейных дифференциальных уравнений с решениями:

И’ т

9---x- + к 29 x = 0, aоб

⁹ х = ^С 1 exp ( Y 1 - ) ⁺ C 2 exp ( V 2 - ) ;

9 у - к 2 9 y = 0,

9 у = С 3 sin ( ky ) + C 4 cos ( ky ) .

Константы С 1, 2, 3, 4 и k определяются условиями однозначности, а параметры γ 1 и γ 2 – по формуле γ 1, 2 = w x /2 a об ± ( w x ²/4 a ² об + k ²)^0,5.

Первым условием однозначности следует при- нять симметричность относительно оси х процесса распространения энергии вдоль оси у

59 у

⁵ У

= 0, у = 0

что приводит к выводу относительно константы С ₃ = 0, и общее решение уравнения энергии будет иметь вид

9 = 9 _х 9 _у = С 1 С ₄ exp ( у 1 x ) cos ( ky ) +

+ C ₂ C ₄ exp ( у₂ x ) cos ( ky ) .

Вторым условием однозначности принимается граничное условие III рода на поверхности теп-ловосприятия у = δ

59 у

⁵ у

у =S

откуда k 5

Nu _об

a

.    ⁹ у =S

^Х об

= ctg ( k 5 ) .

Граничные условия III рода в форме (8), решаемые графически или численно, дают возможность при известной глубине топки 2δ и числе Нуссельта Nuоб ≡ αδ/λоб определить константу разделения k. Корни уравнения (8) kδ = μi представляют сходящийся ряд собственных чисел краевой задачи при i = 1, 2, 3, …, n; решения уравнения (8) достаточно подробно изучены в математическом анализе в применении к краевым задачам теплопроводности. Единственным параметром, влияющим на решение уравнения (8), является число Nuоб, в задачах теплопроводности таким фактором является число Bi; при замене числа Bi на число Nuоб можно воспользоваться обширным справочным материалом [11] по ряду корней при n ≤ 6, при n > 6 можно воспользоваться рекуррентным соотношением μn+1 ≈ μn + π.

По определению число Нуссельта представляет собой отношение двух сопротивлений переносу теплоты: внутреннего по отношению к топочной среде δ/λ_об и внешнего 1/α_с, связанного с теплоотдачей на поверхность тепловосприятия: Nu об = (δ/λ об )/(1/α с ). Численное значение Nu об определяет характер распределения температуры и условий теплопереноса по объему топки КА: при низких значениях Nu об < 1,0, что означает 1/α с > δ/λ об , появляется необходимость интенсификации тепловосприятия поверхности охлаждения, то есть увеличения α с . При Nu об > 1,0, когда 1/α с < δ/λ об , необходимо либо уменьшать размер δ, например, размещением ширм или двухсветных экранов в объеме топки, либо увеличивать λ об , что представляет определенные теплофизические трудности.

Теплоотдача на экранную поверхность αс, Вт/м2·К, происходит двумя механизмами – излучением αл и конвекцией αк: αс = αл + αк; так как в топках основная роль принадлежит излучению, рационально вклад конвекции привести к радиационному теплопереносу с помощью системы корректирующих множителей. Достаточно обширный и достоверный материал в этом направлении отражен в котельных нормах в виде рекомендаций по расчету коэффициента тепловой эффек- тивности экранов ψэ, учитывающего их загрязнение и участие в поверхностном теплообмене ψэ = (qпад – qотр)/qпад. Результирующий тепловой поток на экранную поверхность, таким образом, определяется по зависимости qрез = ψэ·qпад, Вт/м2, а суммарный коэффициент теплоотдачи рассчитывается по формуле αс = qрез /(Т – Тст). Далее, результирующий тепловой поток рационально определять через радиационный qл с учетом вклада конвекции qрез = qл(Во + 1), где Во = qк /qл – число Больцмана.

Для радиационного теплового потока излучающей среды на экран с поглощательной способностью А _ст можно применить формулу [12, 13]

q _л

С ( Т 4 - Т с ⁴ т ) (V А ст - 12 )

и с учетом изложенных выше выводов qрез

У э С ( Т ⁴ - Т СТ ) ( Во + 1 ) (V А ст — 12 )

получаем зависимость для определения суммарного коэффициента теплоотдачи на поверхность топочных экранов ас

У э С ( ^{Во +} 1 ) ^{( Т 4 Т 4} ) ( 1 А ст - 12 ) ( Т - Т ст )

₌ У э ^С о ^{( Во + 1 ) Т 3}

- ( 1 А ст -12 )     ⁽ ) ,

где F(T) = [1 + (Тст /Т) + (Тст /Т)2 + (Тст /Т)3]. В работах [12, 13] отмечается, что многочлен F(T) близок к единице и его можно не учитывать, но численный анализ показывает, что величина этого множителя снижается от 3,75 до 2,75 при увеличении θ = Т – Тст от 0 до 400 К; поэтому можно принять среднее значение F(T)ср = 3,25, так как введение функции F(θ) = 3,75 – 2,5·10–3θ делает задачу нелинейной. Также рационально Аст заменить на ψэ и привести λоб к λл посредством коэффициента bоб = λоб/λл, где λоб может включать все диссипативные механизмы, описываемые диффузионными соотношениями типа законов Фурье и Фика. Таким образом, число Нуссельта можно определить по формуле

X ас5

^Киоб ^s Л— λ_об

= 0,61BU

3 У э к ср 5 ( Bo + 1 ) ^ 0 T ³ F ( T ) ср

У э

(1 У э + 12 ) с о T³ b об ( Во +1 )

( 1 У э +12 ) b о _б

.

ло

Полученное соотношение для Nu_об, где Бугера введено давление в топке р ,

в чис-МПа,

Bu = ксрp5 , позволяет определять Nuоб с исполь- зованием нормативных методов расчета [3].

При введении граничного условия при х = 0 определяется температура среды Т = Т н или θ н = Т н – Т ст , подстановка этих условий в решение (4) дает

С 1 + С 2 =0 н ,                             (13)

и решение уравнения (5) при С ₃ = 0 с учетом совокупности корней μ _i приобретает вид

n

0н =Е Ai cos (ц iY), i=1

где Y = y /δ.

Коэффициенты А_i определяются при подчинении решения (13) условию θ н = const c учетом четности функции косинуса

A =   6н ■ 2sin цi

¹   ц i + sin ц i cos ц i ’

при этом решение уравнения (5) приобретает вид

6 у =6 н E     2^^n^ i    cos ( ^ Y ) .      (16)

ц i + sin ц i cos ц i

Для получения констант С _{1, 2} необходимо ввести граничные условия при х = 0 и х = h, где h – расстояние от выхода из ЗИГ до середины выходного окна топки, м. При х = 0 получено решение (13) С 1 + С 2 = θ н , при х = h граничные условия III рода

• ⁵⁰ —     -  ^ac A

  -"r-A

A                 A dX — - hA или

0 — - h

^   ■ d0 - ^

^a c I ^{d —} J — - h ’

что при подстановке в уравнение (4) дает

^C 1 Y 1 exp ( Y 1 ^h ) + C 2 Y 2 exp ( y 2 ^h ) ^-

“c [C1exP (Y1h) + C2 exP (Y2h)].

^ об

Совместное решение уравнений (13) и (18) относительно С 1 и С 2 дает:

_{C -}      ⁰ н ( ^в 2 /Р 1 ) e^xP ( Y 2 ^h )

1     1 -(₽2 /Р1 ) exP (Y2-Y1) h ’ c2 -0н - C1 -           "------,

1 -(₽2 /Р1 ) ехр(Y2-Y1 )h и решение для распределения температуры по оси х будет иметь вид

0 — - С1ехр ( Y1—) + C2ехр ( Y2 — ) - "нехр ( Y2 — ) x x 1 -(p2 /Р1 ) ехр [(Y2 -Y1 )(h - x)] 1 -(P2 /Р1 ) exP (Y 2-Y1 ) h

В решении (21) введены сокращения: β 1 = α с /λ об + γ 1 ; β 2 = α с /λ об + γ 2 , где γ 1 и γ 2 определяются из условий (4), (5), а θ х и θ у – из соотношений (16) и (21), причем А i = θ н D i . Таким образом, общее решение в безразмерном виде определяется перемножением θ _х и θ _у и делением на θ_н²:

"

" н       i - 1

_x 1- ( p 2/ P1)e ^xP[ C ^Y2£Y1) ( h Z ^x )]

• ^{1    -} ( P 2 /Р1 ) exP ( Y 2 ^- Y 1 ) ^h

  
  

Изложенную выше математическую модель процессов теплообмена в топке, включающую только основные факторы влияния, можно классифицировать как парадигму теплообмена в топках КА. Последующие анализ и адаптация основных положений модели к условиям реальных процессов позволяют выявить достоверность и надежность математической модели.

Анализ и адаптация математической модели

При подстановке предельных значений аргументов х и у решения должны приводить к исходным условиям однозначности. При подстановке х = 0 решение (20) дает очевидный результат θ _х ≡ θ_н. В выходном сечении топки при х = h получается температура, которая в принятых методиках расчета определяется как «температура газов в конце топки t" _т » , но для более точной адаптации этого фактора необходимо определить среднюю по сечению выходного сечения температуру.

Средняя по сечению температура при заданных условиях однозначности определяется интег- рированием функции распределения температуры по координате у:

0 -- ilcos (ц 1У/5)dy - sin"^,(23)

• 5    0

и далее определяется безразмерная средняя температура по выходному сечению топки при x = h :

0ср -^^ 2+2^ Цicosx i-1 Hi +Hi sin Hi cos цi exP(y2h)

1 -P 2 /Р1

1 ^{- ex} P [ ( Y 2 ^-Y 1 ) ^h ]P 2 /Р1

Определенная по формуле (24) температура t _ср = θ²_н·Θ_ср/θ _х + t _ст должна в той или иной мере соответствовать размерной температуре t" _т.

Для адаптации полученного решения (22) к реальному температурному полю топки КА необходимо граничные условия III рода (8) привести к безразмерному виду

• - Nu об © Y - 1 . (25)

Y - 1

d© d Y

Причем производная по безразмерной температуре на поверхности теплоотдачи имеет собственный знак минус, так как в направлении у температура топочной среды снижается, и продолжение касательной к температурной кривой пересекает плоскость Θ = 0 в точке A, расположенной на расстоянии YA от поверхности теплоотдачи. Так как эти соображения построены без учета продольной координаты х, то следует признать, что все касательные к температурным кривым пересекаются в одной точке А. Определив тангенс угла наклона касательных через геометрическое отношение (ΘY=1): YA, получим

NU oб © Y - 1 -© Y - 1 / Y ^

и далее

Y a - VNU oб .                             (26)

Из соотношения (26) следует важный вывод: обобщенное число Нуссельта оказывает существенное влияние посредством расположения точки схождения всех касательных к температурным кривым – точки А , на форму температурных кривых в топке и характеризует эффективность теплообмена в топке КА. При низких числах Нуссельта Nu_об → 0 координата точки А стремится к бесконечности Y A → ∞ и все изотермы в топке стремятся стать параллельными прямыми; это говорит о низких значениях α с и поперечного размера топки δ, а также о высоких значениях обобщенного коэффициента теплопроводности λ об . При высоких значениях Nu об → ∞ все изотермы в топке сходятся в одну точку, расположенную на поверхности теплоотдачи при ее пересечении с линией Θ = 0, то есть при t = t _ст (см. рисунок). Рекомендации относительно α_с, δ и λ_об при этом противоположны предыдущим.

Для предотвращения шлакования поверхно-

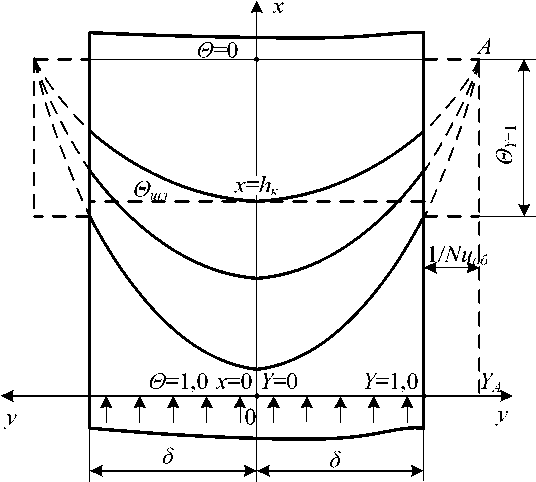
Температурное поле в топке котельного агрегата в стационарном режиме: 0 = 0 х 0 у /02 , Y=у /6, х = h к - координата выходного сечения топки (симметричная задача)

стей нагрева в пароперегревателе при сжигании твердого топлива ограничивается температура на выходе из топки t"т, на газомазутных котлах эту температуру ограничивают по условиям надежной работы металла пароперегревателя и по экономическим соображениям. Разработанная математическая модель теплообмена позволяет достаточно быстро определить надежную относительно шлакования высоту топки hшл. При определении Θшл = (tшл – tст)/(tн – tст) можно сформулировать условие отсутствия шлакования так: 0шл > 0х=0 , так как максимальная температура наблюдается на оси потока при у = 0, а условие х = h соответствует выходному сечению топки. При подстановке этих условий в соотношение (22) и решение его относительно h получается зависимость hшл = in [®шл - М1 exp Y2 - M2 exp (Y2 -Y1 )]-

- In ( M 1 + M ₂ ) ,                          (27)

где М 1 = D 1 [1 – (β 2 /β 1 )], M 2 = Θ шл (β 2 /β 1 ); также содержание величин γ 1 , γ 2 , β 1 , β 2 раскрывается в зависимостях (4), (5), (21). Примененный в формуле (27) первый корень уравнения (8) точно соответствует малым числам Нуссельта, при увеличении Nu об появляется необходимость учета корней μ 2 …μ n .

Решение для топок призматической и цилиндрической форм

Разработанная математическая модель (22) описывает стационарное двумерное температурное поле в объеме топки t = f(x, y) при условии отсутствия теплоотвода в направлении оси z, чтобы учесть теплоотвод в этом направлении по анало- гии с осью у, необходимо установить ряд условий. Геометрия размещения поверхностей тепловос-приятия в направлении z должна быть аналогична таковой в направлении у, но коэффициенты теплоотдачи в общем случае могут быть разными αс,z ≠ αс,у. Температуры поверхностей тепловос-приятия должны быть одинаковыми tст,z = tст,у, так же как и начальные температуры потока среды tн,z = tн,у, иначе не соблюдается естественный масштаб температур. При соблюдении этих условий температурное поле в направлении оси z можно описать уравнением, аналогичным уравнению (16),

0 z =0н £---—   cos (^ ) = i= 1 Ц + sin Цi ■ cos цi

= 0 н F ( z ) .                                   (28)

Корни характеристического уравнения, иначе собственные числа краевой задачи μ _i , можно определить при Nu_об = Nu_{об, у} по зависимости (8), если числа Нуссельта по осям у и z различаются, то нет формальных препятствий для расчета Nu об, z и решения уравнения, аналогичного (8), но для оси z. В результате трехмерное температурное поле в топке призматической формы можно описать зависимостью

0 = 0 у 0 у 0 _z =0 н F ( % ) F ( y ) F ( z ) ,          (29)

или в безразмерном виде

0. 0 .0_

0н где функции координат определяются по зависимостям:

n

F ( x) = £ exp (Y2 x )x i=1

x 1 -(P2 /Р1 ) exP [(Y2 -Y1 )(h - x)]

1 -(P2 /Р1) exP (Y 2-Y1) h’

F (y ) = £----2sin^i    cos (^y),(32)

i = 1 Ц i ⁺ sin Ц i cos Ц i

F(z) = ^    2swi    cos^).( i=1 Цi + sin Цi cos Цi

Для осесимметричного потока среды в канале цилиндрической топки КА дифференциальное уравнение переноса теплоты имеет вид d29 1 59 d29 w d29 л

+     +    - x = 0, dr 2 r dr dx 2 a об dх 2

что дает возможность написать с применением метода разделения переменных уравнение для θ _r вместо (5):

9 Г + - 9 Г + k 2 9 r = 0 r

с решением f ^

9 r = C 5 1 0 ( kr ) = C 5 1 o |- I.                 (36)

I r o J

В этих зависимостях координаты цилиндрической системы: 0 ≤ х ≤ h – продольная координата, 0 ≤ r ≤ r0 – радиальная координата, угловая ко- ордината ψ не учитывается, так как температура по окружности не изменяется вследствие осевой симметрии ∂θ/∂ψ = 0. Для θх сохраняются форма уравнения и решение (4). В уравнении (29) I0 – четная функция Бесселя первого рода нулевого порядка, в аргумент которой входит корень ε = kr0, определяемый граничными условиями III рода на цилиндрической поверхности охлаждения при r = r0:

d9 _r

—^c- 9

^ об '

При подстановке в уравнение (37) решения (36) получаем характеристическое уравнение для определения констант ε, что приводит к сходящемуся ряду чисел εi, определяемых через фактор Nuоб = αсr0/λоб,

S i = NU 06 Iy^, . (38) 1 1 ^(e i )

В знаменателе уравнения (38) записана нечетная функция Бесселя первого рода первого порядка, определяемая по зависимости I 1 (ε i ) = – ∂ I 0 /∂r . Все отмеченные выше особенности чисел μ _i характерны и для ε _i .

Рассмотренная выше математическая модель основана на процессах в однородной топке, имеющей неизменное сечение по оси х с однородными граничными условиями. Но нет формальных препятствий для расширенного применения при рассмотрении неоднородных по оси х топок – в этом случае необходимо высоту топки разбивать на зоны с однородными условиями по схеме, предложенной в [9] и реализованной в [6–8, 10]. Уравнения (22) и (27) допустимо использовать для определения высоты топки и по другим, кроме вопросов шлакования, ограничениям: по термической стойкости металла в поверхностях теплообмена, по режиму теплообмена пароводяной среды в трубах, по технико-экономическим соображениям при оптимизации и т. п.

Заключение

Применение нового метода математического описания теплообмена в основном объеме топки КА, определяемого как парадигма теплообмена в топках, позволило сформулировать и решить двух-и трехпараметрическую математическую модель теплообмена, связанную с коэффициентами переноса и температурным полем в объеме топки.

Идентификация основных характеристик температурного поля как расчетных параметров нормативного метода [3] позволяет достоверно определить эти характеристики для различных типов КА и видов применяемого топлива. Обобщенное число Нуссельта определяет характер температурного поля и интенсивность теплообмена в объеме топки КА; в качестве расширенного применения парадигмы теплообмена показано применение ее для топок призматической и цилиндрической форм.