Математическая модель обоснования вариантов реконфигурации распределенной автоматизированной контрольно-измерительной системы

В настоящее время в промышленности и научных исследованиях наблюдается существенный рост требований к контрольноизмерительным системам с точки зрения их при-спосабливаемости для достижения оптимальной адаптации к конкретной измерительной задаче с целью обеспечения наилучших показателей быстродействия, точности и помехоустойчивости, пропускной способности и функциональ- ной избыточности. Потребность в контрольноизмерительных системах, обладающих такими свойствами, существует в различных сферах деятельности, в числе которых - компонентные тестирования и мониторинговые исследования быстропротекающих процессов при испытаниях ракетно-космической техники, а также динамический мониторинг конструктивной целостности в процессе ее эксплуатации. На сегодняшний день таким потенциалом обладают только автоматизированные контрольно-измерительные системы с пространственно распределенной модульной компоновкой (далее - РАКИС). Они позволяют использовать только то количество измерительных модулей, которое требуется для решения измерительных задач, что позволяет оптимизировать затраты, а распределенное решение обеспечивает оптимальное отношение результативности и ресурсоемкости, в особенности для крупногабаритных измерительных установок. Так, например, измерительные модули могут располагаться локально вблизи точек измерений и соединяться через последовательный интерфейс. За счет этого снижаются требования к проводке, достигается легкость в обслуживании и, что очень важно, короткие кабели датчиков делают результаты измерений менее чувствительными к помехам и, таким образом, более стабильными и точными.

Однако, как показал опыт применения такого рода РАКИС, зачастую имеющихся аппаратных возможностей с фиксированными алгоритмами измерительных циклов оказывается недостаточно для более эффективного решения возложенной на РАКИС контрольно-измерительной задачи. Выяснилось, что без обеспечения возможности динамического изменения режимов работы РАКИС (изменение последовательности измерений, настроек синхронизации, типа входа и вида измеряемой величины и т.д.), причем в автоматическом режиме, значимого повышения эффективности работы РАКИС не добиться. Соответственно возникла необходимость в разработке научно-методического обеспечения создания распределенных автоматизированных контрольно-измерительных систем с автоматической реконфигурацией. Следует отметить, что задачи максимально полного использования вычислительного ресурса и обеспечения эксплуатационной надежности (резервирования) такого рода оптимальных и адаптивных систем в большинстве своем решены в рамках теории автоматического управления (регулирования) [1-5]. Однако вопросы моделирования процедуры многокритериального выбора конфигурации

РАКИС посредством априорного сравнительного оценивания различных вариантов и сегодня остаются одной из центральных проблем повышения их эффективности. Существует ряд сложных моментов, затрудняющих решение этой проблемы. В частности, ряд переменных, отражающих влияние внешних факторов (условий) проведения измерений (электромагнитные помехи, вибрации, солнечная радиация, состав газов и параметры их динамических состояний и т.д.) при оценивании показателя результативности на этапе анализа вариантов формирования оптимальной конфигурации РАКИС, может быть оценён лишь приблизительно, с указанием примерного интервала возможных значений и ожидаемого распределения на этом интервале. Сам процесс обоснования решения на реконфигурацию осуществляется в условиях ограниченного объёма информации об ожидаемых характеристиках результата реконфигурации, а опыт лица, принимающего решение (специалиста в области технологии измерений и контроля), может выражаться в виде вербальных описаний. Кроме того, нужно учесть, что современные образцы РАКИС являются достаточно сложными и для их описания необходимо использовать векторные показатели с большим числом компонент.

Многомерность сравниваемых альтернатив и существенная степень неопределённости оценивания показателей приводят к необходимости отнесения задачи сравнения вариантов реконфигурации РАКИС к классу задач многокритериального выбора в нечёткой среде.

В указанных выше условиях актуальной научной задачей является разработка математической модели обоснования вариантов реконфигурации РАКИС с максимально возможным использованием ее аппаратного ресурса на основе нечётких моделей.

Постановка задачи исследования

Общая постановка задачи в этом случае выглядит нижеследующим образом.

Пусть:

Z = { z_x }, ( 1 = 1, L ) - множество вариантов реконфигурации РАКИС;

X = { X} }, ( i = 1, n ) - множество частных показателей оценивания вариантов реконфигурации РАКИС;

A = {а ,} - множество значений частных ^~       ^~ li показателей Х;

G = { g i } - множество значений коэффициентов важности частных показателей Х ;

~ _й = {( f l ( x ), H a l, [( f l ( X )]} - результат нечёткого оценивания , -го частного показателя 1 -го варианта;

ВЕСТНИК 2016

f l ( x ) = x i ^ [0,1];

Ца , [(f (Х)] - функция принадлежности ^~ l нечёткого множества ~ ц ;

gi = {(gi,E (gi)} — результат нечёткого оце-~х нивания коэффициента важности г-го частного показателя из множества Х;

E g, ⁽ g i ) - функция принадлежности нечёткого мн о жества g i .

Решение ~

Решающее правило для выбора лучшего ва- рианта виде:

где E l

реконфигурации РАКИС выражается в z * = arg max El, le1, l ~

- значение обобщённого показателя для l-го варианта реконфигурации РАКИС, Et = est (A , G).

,~                                                               ,■ •

ВЕСТНИК 2016

Вычисление обобщённого показателя E l , как следует из выражения (2), связано с проведением определённых преобразований над нечёткими векторами А ~ и G . Естественно, что и результат такого преобразования будет представлен в нечёткой форме. Предлагается для вычисления по формуле (2) применить нечёткий интеграл [6]. При этом

E i = ^est i ( A , G ) = maxmin{ a _u, g _x ⁽ X a ^)} .

—                     a г. eA          —

,—                          ,—

Здесь gx (Xa ) — нечёткое значение обобщённого коэ~ффициента важности показателей из множества Х, входящих в множество Ха, дл(Ха) = {(дл(Xa), Egx(дл(Ха))}, (4) ~ ~ где дX(Ха) - обобщённый коэффициент важности группы частных показателей, входящих в множество а-уровня, д^ (ха) = д^{x I fl(х) > а}.           (5)

Вычисление по формуле (3) требует предварительного задания способа вычисления по формуле (5) и правил сравнения нечётких множеств.

Вычисление по формуле (5) требует введения понятия нечёткой меры. Для данного случая наиболее удобной мерой является так называемая X-мера (мера Сугено) [7]. Для X-меры справедливо следующее выражение: ГК. Л 1 Г К дл I Ux | = у П(1 + Л?2(х))-1 v i=1 ) л l i=1

Иными словами, если известны коэффициенты важности отдельных показателей x,, i = 1, К, то важность группы показателей из К элементов может быть вычислена по формуле (6). Кроме того, для упрощения вычислений исходные нечёткие множества ~ li и д, представляются в трапецеидальной форме. П~ри этом любое такое нечёткое множество может быть описано кортежем из четырёх чисел. Например, нечёткое множество M записывается в виде M = (m, m, а, в), где [m, m] - ядро нечёткого интервала; [m-a, m+вА - носитель нечёткого интервала; т. - нижнее модальное значение; m- верхнее модальное значение; а - левый коэффициент нечёткости; в - правый коэффициент нечёткости. Тогда исходные данные для сравнения вариантов реконфигурации РАКИС можно записать в виде:

~ _и = ( а ^, ^a ii , а_и , Р), ⁽⁷⁾

g i = ⁽£, g„ a ^{в )}. (₈)

При задании исходных данных в форме выражений (7) и (8) значение X -меры также будет нечётким:

~ = ( X , X, а„ в , ).

При этом, используя условие

2 л

K

П ⁽¹ + ^Л д _х ( x )) ^{- 1}

i = 1

= 1,

можно производить вычисление X j (j' =

1,2,...,4)

по следующим д ^

g 1 = g, ^-a, ^; g 2 = g i ; g з = g , ;

g 4 = g_i + в , ⁽рис. 1).

По результатам вычислений строится нечёткая X -мера (9) следующим образом:

Л = Л 3 ; Л = Л , ; а_л = Л 3 - Л ₄;

Р л = Л 1 - Л

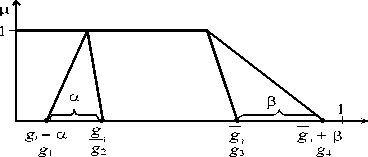
Рис. 1. Построение нечёткой X -меры

При условии задания X -меры в виде выражения (9) вычисление д _x ( X _a ) по формуле (4) не представляет труда. ~

Для сравнения нечётких чисел целесообразно использовать метод сравнения нечётких интервалов [6], который предполагает вычисление и последующее сравнение двух векторов A _<4> и B < ₄ > . В случае если A < ₄ > > B < ₄ > , делается вывод о том, что нечёткое множество A >  B . Векторы формируются следующим образом:

^A <4> = ^{ a 1 , a 2 , a 3 , a 4 ^},

B<4> = {b 1, b2, b3, b4}, где a1 = POS(a > b) = max (0,min (1,1 + (a - b)/(pa + ab)));