Математическая модель обработки геологических проб

Поставим следующую задачу: определить размеры частиц пробы после дробления и степени сокращения ее массы на этапах так, чтобы затраты энергии на дробление материала были минимальными, а погрешность содержания, вызванная многоэтапной обработкой, находилась в заданных пределах [3].

Для решения этой задачи необходимо установить зависимость затрат на дробление от размеров частиц и массы пробы и найти математическое выражение для численного критерия эффективности той или другой схемы обработки. Рассмотрим оценку расхода энергии на дробление. В зависимости от крупности дробленого материала условно разделяют стадии дробления и измельчения: крупное дробление — от 1500 до 100 мм; среднее дробление — от 100 до 40 мм; мелкое дробление — от 40 до 5 мм; измельчение — от 5 до 0,1 мм; тонкое измельчение — от 0,1 до 0,05 мм.

В дальнейшем, независимо от размеров частиц, будет использоваться только один термин — дробление. Важная количественная характеристика — степень дробления i , которая определяется как отношение максимальных размеров частиц до ( D ) и после ( d ) дробления: i = D/d.

Степень дробления на каждом этапе обработки назовем частной:

i_k = _d ^k _k ^{- 1} , k = 1,2,..., n, степень дробления, достигнутая за все этапы, — общая и равна произведению частных степеней:

_{ii i =} ^d 0 ^d 1 ^d n-1 ₌ ^d 0 _{= i}

• ^{12    n} d ₁ d ₂ d _n d _n

С уменьшением размеров частиц в них уменьшается число крупных дефектов, облегчающих разрушение, поэтому удельная прочность частиц возрастает. Для горных пород это заметно для частиц размерами меньше 0,1‒0,5 мм [1]. Таким образом, существенными факторами, влияющими на затраты энергии на дробление, являются степень дробления и размеры измельчаемых частиц.

Работа на дробление одной частицы размера D до размера d определяется с помощью законов дробления [1]. В 1867 г. П. Риттингер, рассматривая дробление одиночного куба на более мелкие, предположил, что работа прямо пропорциональна вновь образованной поверхности и выражается через D и d следующим образом [1]:

A = K р( _d ¹ - _D ¹ ) Q = K р ( ⁱ _D ^{- 1}) Q , где К _р — коэффициент пропорциональности; Q — масса пробы.

3акон дробления Кика — Кирпиче-ва (1875) утверждает, что работа на дробление пропорциональна объему тела. В этом случае зависимость от D и d имеет более сложный вид:

А = К k (lg D — lg d ) Q = К k Q lg i .

Ф. Бонд в 1951 г. предложил считать затраты энергии на дробление пропорциональными среднему геометрическому из объема и поверхности куба, что соответствует формуле:

А = K_r(-U--U)Q= K-^Xq.

• ⁶    Jd Id ⁶ Jd ~

Закон Кика — Кирпичева применяется для оценки затрат энергии на стадиях крупного и среднего дробления. Так как при обработке проб размеры частиц можно отнести к стадиям мелкого дробления, то применение этого закона исключается. Считается, что при мелком дроблении применим закон Риттингера, а закон Бонда занимает промежуточное положение.

Формула для подсчета энергии по закону Риттингера хорошо согласуется с существующими нормами затрат труда

Таблица норм времени на механическое дробление при обработке проб

Категории крепости пород	Размер частиц, мм								K
	25‒11	10‒6	5‒3	2.5‒1.1	1.0‒0.6	0.5‒0.3	0.25‒0.15	0.14‒0.07
Ι ‒ ΙΙΙ	0.005	0.008	0.018	0.034	0.061	0.1	0.196	0.5	0.09
	0.10	0.12	0.13	0.07	0.09	0.08	0.07	0.07
ΙΥ ‒ ΥΙ	0.006	0.011	0.025	0.047	0.073	0.128	0.242	0.55	0.11
	0.12	0.19	0.19	0.09	0.11	0.10	0.08	0.08
ΥΙΙ ‒ ΙΧ	0.008	0.013	0031	0.064	0.84	0.148	0.285	0.615	0.14
	0.16	0.20	0.23	0.12	0.13	0.11	0.11	0.09
Χ ‒ ΧΙ	0.012	0.018	0.064	0.088	0.125	0.190	0.348	0.678	0.19
	0.24	0.27	0.48	0.17	0.18	0.14	0.13	0.9

Примечание: В числителе — затраты времени на дробление; в знаменателе — трудоемкость (коэффициент К ).

на дробление при обработке проб. Нами были приняты нормы времени на механическое дробление проб, взятые в зависимости от крепости пород и размеров частиц. Эти нормы выработки, являющиеся обобщением большого производственного опыта и специального хронометража, приведены в справочниках укрупненных сметных норм (см. таблицу), где N обозначены затраты времени в человеко-часах на 1 кг пробы. Считая, что затраты времени прямо пропорциональны затратам энергии, т.e. N = K (l /d — 1/ D ), можно определить коэффициент для различных степеней дробления:

КN = NDd/(D — d).

Из данных таблицы видно, что более всего отличается от остальных значений коэффициент К , отвечающий дроблению от D = 5 мм до d = 3 мм.

При вычислении среднего значения наибольшее и наименьшее значение коэффициента отбрасывались. Величины К для пород одинаковой крепости ʜe-значительно отличаются для различных степеней дробления, а коэффициент K позволяет достаточно точно оценить затраты времени в соответствии с существующими нормами. Например, на дробление 1 кг пород IV — VI категории крепости от размера D = 10 мм до размера d = 0,06 мм по существующим нормам отводится N ₁ = 0,011 + 0,025 + 0,047 + 0,073 = 0,156 чел.-ч., а затраты по формуле, связанной с законом Риттин-гера N ₂ = (1/ d — 1/ D ) K_N = 0,172. Если же рассмотреть дробление 1 кг пород Х — XI категорий от размера D = 25 мм до размера d = 1,1 мм, то получим со-

, авᴦуᴄᴛ, 2004 ᴦ., № 8

ответственно N ₁ = 0,175 и N ₂ = 0,165.

Поэтому для оценки затрат энергии А на дробление при многоэтапной обработке проб нами использовался закон Риттингера. Работа на каждом этапе А_k вычисляется по формуле

Ak = K.. - 577 )Qk -1 = kk

= K( -

Q 0 ^dk ^dk -1 m k -1

а суммарная затраченная энергия —

n

A = K Z (- 7T1-),

Q 0 k = 1 d k   d k - 1 m k - 1

где т ₀ = 1. Постоянный множитель К/Q ₀ не влияет на значения размеров частиц и степеней сокращения, при которых функция затрат достигает наименьшего значения. Поэтому оптимизация обработки проб есть задача минимизации функции:

, 1 £ / 1 1.1

v4 — I- Z 677     77    )

^dl _kyd_k d_k_/m_k__x при ограничениях

^dk(mk-mk_x)<^

d 0 ≥ d 1 ≥ ... ≥ d n ≥ d,

f(x^k) <  f(x^{k -1} ). ¹ ^ m 1 <  m 2 <  ... m n -1 <  ^m , где А — функция затрат энергии; d_k — размеры частиц пробы на этапах обработки после дробления, см; m_k — степени сокращения массы пробы; σ — предельно допустимая погрешность, доли единицы; Q ₀ — масса начальной пробы, г; γ — средняя плотность материала, r/см³, С — контрастность руды; δ — наименьший технически возможный размер частицы после дробления, определяемый комплектом механизмов, см; т — степень общего сокращения массы пробы.

Решение поставленной задачи определяет эффективную cхeмy обработки проб, удовлетворяющую и требованиям минимизации затрат, и требованиям необходимой точности.

Оптимизация обработки проб относится к классу задач минимизации функции многих переменных при некоторых ограничениях: min f ( x ) при х ∈ Х , где х = ( х ₁, х ₂,..., x _n) — точка n -мерного пространства, а Х — некоторое подмножество этого пространства [2]. Подмножество называется допустимым множеством задачи минимизации, а точки, принадлежащие к Х, — допустимыми точками. В нашем случае размеры ча-

стиц d_k и степени сокращения массы пробы m_k определяют точку x = ( d ₁, ..., d_n , m ₁ , ..., m_{n- 1} ), а вышеприведенные неравенства задают допустимое множество.

Точка х называется решением задачи минимизации, если она является допустимой, и для всех остальных допустимых точек выполняется неравенство: . Решение задачи может быть единственным, их может быть несколько. Множество решений может быть бесконечным.

Справедлива теорема Вейрштрасса, позволяющая выделить широкий класс задач минимизации, имеющих решение: задача минимизации непрерывной функции f ( х ) на замкнутом ограниченном множестве Х разрешима. Непрерывная функция может достигать наименьшего значения либо в некоторой внутренней точке допустимого множества, либо на его границе. При решении задач минимизации важную роль играет градиент функции f ( х ), т. е. вектор, координаты которого — частные производные:

X ox^ dr_n

Если минимум функции f ( х ) достигается во внутренней точке , то градиент в этой точке обращается в нуль:

.

Градиент определяет направление наискорейшего возрастания функции. Это свойство используют для построения некоторой последовательности точек из допустимого множества х ¹, х ²,..., x^k ,..., таких, что значение функции убывает от точки к точке, т.е. выполняется неравенство

Методы построения подобных последовательностей называются методами спуска. Такую последовательность можно построить, перемещаясь от точки к точке в направлении, противоположном градиенту, что обеспечивает убывание функции:

xk+1 = xk - akf (xk), где ak — некоторое положительное число, называемое шагом спуска.

Иногда, в целях уменьшения объема вычислений на каждом этапе спуска изменяют значения не всех, а одной или нескольких переменных, полагая остальные постоянными и изменяя их на последующих шагах. Такой метод называется методом покоординатного спуска.

В том случае, если задача минимизации имеет вид min f ( х ), при ограничении g ( х ) = 0, для решения задачи используют метод множителей Лагранжа. При этом составляют функцию Лагранжа L( х , λ ) = f ( х ) + λ g ( х ) и находят значения х и λ , в которых градиент функции Лагранжа обращается в нуль. Для этого необходимо решить систему уравнений:

15L   df   d gg ■ m

=      +        , i = 1,2,.... n,

dx.   dx.     dx.1           1 i

9L

— = g(x) = 0

VOA

Решениями этой системы могут быть одна или несколько n -мерных точек. Сравнением значений функции f ( х ) в этих точках можно определить наименьшее значение.

Для решения системы уравнений будем использовать метод последовательных приближений. При этом система приводится к виду хi = ϕi(х1, х2,..., хn), i = 1, 2,..., n.

Выбирается некоторое начальное приближение к решению системы x ⁰ = (x 0 ,x⁰,...,x П ) ,а каждое последующее приближение находится из соотношений:

kk- 1 k- 1 k- 1 ^xi = v' ^x 1 , x 2 ,—, x n )

При выполнении некоторых условий последовательность х ¹, х ²,..., х^k ,... сводится к решению указанной системы уравнений.

Задача оптимизации обработки проб — частный случай задачи минимизации функции:

n

F(x,y) = 10а + Z (Да - ^)^ ^y 1    k =2 ^yk ykA ^xk-1

при ограничениях

ye (x-1)+ v ye(xk - xk-1)+

+ У^(т - xn-1) < D b ≥ y1 ≥ y2 ≥ ... ≥ yn ≥ a > 0,

1 ≤ x ₁ ≤ x ₂ ≤ ... x _n-1 ≤ m , где а ≥ 1, β > 1.

Ограничения этой задачи определяют замкнутую ограниченную область, в которой функция F ( x, y ) непрерывна, так как х _i > 0, y _i > 0. Следовательно, по теореме Вейрштрасса задача минимизации имеет решение, поиск которого состоит из нескольких этапов.

, авᴦуᴄᴛ, 2004 ᴦ., № 8

Этап 1. Зафиксируем переменные х ₁, х ₂,..., х _n-1 и введем обозначения:

a 1 = 1- —

^x 1 ^,

= 1 ___ 1_

° ^k x k - 1 ^xk ’

k = 2,3 ,...,n - 1,

an = x v x n -1

b1 = x1 — 1, bk = xk — xk-1, k = 2, 3,

...

, n — 1,

b_n = m — x_{n -1}.

Рассмотрим задачу минимизации функции

n

FO = £ a k /y a k = 1

при ограничениях

£1 bye5 D• b ≥ y1 ≥ y2 ≥ ... ≥ yn ≥ a > 0, где аk > 0, bk > 0. Эта задача имеет единственное решение, которое находится методом множителей Лагранжа:

(*)

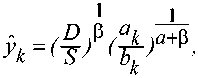
n ¹ где: 5 = £ (a l b a ) ^{a +e} . k =1 ^{k k}

Этап 2. Подставив значение в функцию F ₁(y), получим ^.

Таким образом, задача минимизации функции F (х, у) сводится к минимизации функции

• — 1 n-2 x, —x, , _ 1 у к k-Y !

(™-xn_x)X"P

+ xP 1

77-1

при ограничении

1 ≤ x ₁ ≤ x ₂ ≤ ... ≤ x _n-1 ≤ m , где р = β /(а + β ). Решением этой задачи является решение системы уравнений:

_x _ p ^xi"^xi^p .

1 Y-p x^P -1 ’

. p ^^,-^Xn-\4_l-l-^Vm-^Xn-^^Pxn-0

”"1 \~P (m-x .}P-xP обозначим решение этой системы

.

Этап 3. Подставляем значения в соотношение (*), получим оптимальные значения переменных

J к

• v, =)

;

;

• к 1 S(\)' 1 xk lxk’

Приведенный метод позволяет решать задачу оптимизации обработки проб для произвольного числа этапов и любой заданной точности.