Математическая модель образования и движения анионных вакансий при восстановлении металлов в комплексных оксидах

Интерес к бескоксовым способам извлечения железа постоянно растет, повышается необходимость вовлечения в производство бедных и комплексных руд. Следствием этого явилось большое количество работ, посвященных изучению процесса восстановления железа из различных рудных и нерудных материалов с использованием углеродсодержащих восстановителей разного качества. Однако в результате сложности состава рудного материала картина выделения в нем металла в процессе восстановления сильно отличается от результатов восстановления железа в богатых рудах [1–3]. Для бедных и комплексных руд это, как правило, равномерное выделение частиц металла по всему объему оксидной вмещающей фазы. И хотя такие руды обычно являются плотными материалами с низкой газопроницаемостью, восстановление идет с большой скоростью при относительно невысокой температуре [4–6]. Всё это вызывает серьёзные трудности в объяснении механизма восстановления металлов с использований классических положений.

Один из наиболее активно развивающихся подходов к объяснению процесса восстановления металлов из комплексных оксидных материалов основан на рассмотрении твердофазных процессов, протекающих в несовершенных (дефектных) кристаллах [7, 8]. При нагреве в восстановительных условиях кристаллическая решётка оксида насыщена анионными вакансиями (примесными, обусловленными присутствием примесных катионов пониженного заряда, термическими – парными дефектами Шоттки, и восстановительными). Часть вакансий содержит «лишние» (дефектные) электроны. Генератором таких вакансий является восстановитель, который на поверхности реагирования извлекает из решётки оксида кислород, отдавая ему свои валентные электроны, а ранее локализованные у аниона электроны остаются в решётке оксида, удерживаясь электрическим полем. Таким образом, восстановитель взаимодействует не с молекулой оксида металла, а с анионом кислорода кристаллической решетки, например, по реакциям:

( MgFeSiO 4 ) = ( Mg ^{2 +} ) + ( Fe ^{2 +} ) + ( Si ^{4 +} ) + 4 ( O ^{2 -} ) (1) { CO } + ( O ^{2 -} ) = { CO₂ } + ( V a^{2 -} ) (2) ( Fe ^{2 +} ) + ( V a^{2 -} ) = Fe (3) ( Mg ^{2 +} ) + ( Si ^{4 +} ) + 3 ( O ^{2 -} ) = ( MgSiO g ) (4)

( MgFeSiO₄ ) + { CO } = Fe + ( MgSiO₃ ) + { CO₂ } , (5) где V_a ^{2 -} - восстановительная вакансия, содержащая два электрона. В круглых скобках указаны компоненты оксидной фазы, в фигурных – газовой, без скобок – металлической фазы.

Если в ближайшем окружении все катионы обладают равным сродством, то при перемещении вакансии электроны легко переходят от одного катиона к другому, сопровождая вакансию от места появления до места её стока. В местах стока таких вакансий и формируются зародыши металлической фазы.

Данный подход позволяет объяснить высокую скорость процесса восстановления, а также появление металлической фазы внутри объёма оксидной, куда доступ восстановителя отсутствует. Однако он в значительной мере является качественным и не позволяет оценить степень влияния различных физикохимических параметров на скорость процесса восстановления.

В данной работе предпринята попытка перейти к количественному описанию, построить математическую модель, способную учитывать не только химические реакции, протекающие на поверхности раздела руда – восстановитель, но и учесть диффузионные потоки в системе.

Обоснование методики

В качестве основы для разработки модели взяты результаты предшествующих работ [9–12].

Рассмотрим систему, состоящую из частицы руды (фаза Ф), находящейся в атмосфере газообразного восстановителя (фаза V ). Поверхность рудной частицы F является непроницаемой для компонентов обеих фаз, следовательно, восстановитель не может проникать внутрь куска, и все обменные процессы протекают на границе раздела.

Считаем частицу сферической. Введём сферическую систему координат с началом в центре частицы (см. рисунок). Всю систему также считаем сферической. Полагая, что начальное распределение параметров состояния системы (концентраций компонентов, скоростей, температуры и других величин) обладает сферической симметрией. Можно

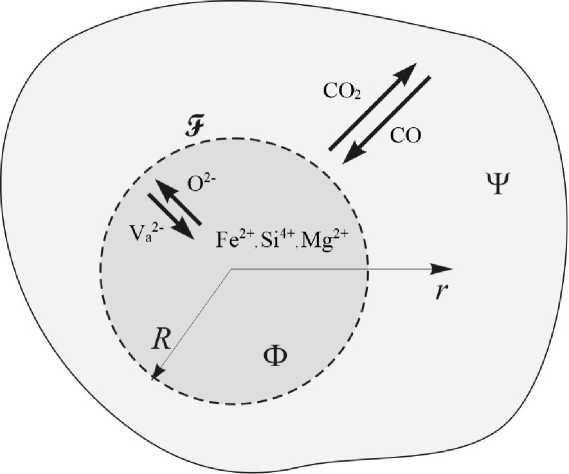
Графическая модель процесса восстановления, протекающего в системе «рудная частица Ф – восстановительная газовая фаза Ψ »

считать, что и в дальнейшем в любой момент времени распределение всех характеризующих систему величин обладает сферической симметрией.

В общем виде химические реакции на поверхности радела фаз можно представить в следующем виде:

« 11 R 1 + - + П 1 m ^R m = P 1 ,

.....................................,                        (6)

1. В фазе рудной частицы Ф протекают процессы теплопроводности и диффузии:

1) уравнение теплопроводности:

д т = х ^Ф ХАГ 2 д Т ) д t р ^Ф c p r ² д r V д r J ,

n n 1 R 1 + — + n nm R m = P n ,

где R 1 , — , R _m - набор компонентов фазы V ;

где T – температура в данной точке; t – время; λ – коэффициент теплопроводности; ρ – плотность; c P - теплоемкость фазы; r ° - расстояние от центра частицы,

2) уравнения диффузии компонентов фа-

P 1 , — , P _n - набор компонентов фазы Ф;

n ij ( i = 1, — n ; j = 1, — m ) - стехиометрические коэффициенты реакций. Причем компоненты одной фазы неограниченно растворимы друг в друге и нерастворимы в компонентах другой фазы.

Для примера допустим, что частица руды (фаза Ф) представляет собой гомогенный газонепроницаемый комплексный оксид следующего компонентного состава: O, Fe, Si, Mg. Газовая фаза V состоит из двух компонентов -СО и СО₂. При достижении температуры на-

зы Ф :

д c ^Ф ₂

О2

д t

= D ^Ф ₂

О2

1 д r ² д r

r

V

чала восстановления активизируются реакции

(1)–(5). Ключевой реакцией, отвечающей за массообмен между фазами, является реакция

(2). Для записи этой реакции в виде (6) преобразуем её с учетом ( O ^{2 -} ) = ( O ) + ( V a^{2 -} ) . Тогда

получим [1] { CO } + [1] ( O ) = [1] { CO₂ } (в квадратных скобках указаны стехиометрические коэффициенты реакции), или

[ - 1] { CO } + [1] { CO 2 } = [1] ( о ) . (7)

Получена запись вида (6), в которой символом R ₁ обозначен CO, R ₂ – CO 2 . Продукт реакций (O) обозначен соответственно P ₁ . Стехиометрические коэффициенты реакций n ij в случае (7) равны n 11 = - 1, n ₁₂ = 1. И хотя в такой записи отсутствуют прямой учет восстановительных вакансий, их количество обратно пропорционально числу удаленных атомов кислорода из решетки оксида ( O ) . Процессы, описываемые реакциями (1), (3), (4), не связаны с массопереносом между фазами Ф и V и потому не включены в рассмотрение. Тем не менее, фаза Ф помимо аниона О^2– содержит катионы Fe²⁺, Si⁴⁺, Mg²⁺, которые могут участвовать в диффузионных процессах, поэтому их также надо учитывать при составлении математической модели.

Ф д c n . 2     О^{2 -}

дr

,

д c ^Ф ₂₊

Fe2+ д t

д c ^Ф ₄₊

Si4+ д t

= D ^Ф

Fe

= D ^Ф

Si

1 д

-²⁺ r ² д r

r ²

V

Г

'4+ r ² д r

r

V

V

Ф

' F

д r V

Ф д c и I

. 2    Si^{4 +}

д r

V

,

,

где c_i – массовая концентрация i -го

компо-

нента; D_i ^o – коэффициент диффузии i -го компонента.

• 2.    В фазе Ψ, окружающей частицу, также протекают процессы теплопроводности и диффузии реагентов. Однако вследствие изменения размеров частицы соответствующие уравнения будут несколько сложнее:

• 1)    уравнение теплопроводности:

д T   X^V 1 д Г ₂ д Т )

• =              r ² +

• д t p^V c V r ² д r V д r J

+

Г пФ   ^

TV^{- 1}

V ^PF     J

R ² dR д Т r ² dt д r ’

где ρ_F – плотность на границе частицы; R – радиус частицы.

2) уравнения диффузии компонентов фазы V :

V ^{д c} CO

+

д t

(„Ф

V ^pF

= D v ± А

^CO r ² д r

V r2 ecC»

V    д r J

+

—

^

V

R ² dR д c C i O r ² dt д r

3. Поверхность раздела фаз:

1) уравнение теплопередачи, связывающее тепловые потоки из фаз Ф и V к поверхности раздела фаз с тепловым эффектом химической реакции (7):

' J [ t, R (t)-0]-x"^- [ t, R (t)- 0]- n

+£ IO AHO = 0, i=1

где I _O – мольная скорость удаления кислорода с единицы площади поверхности раздела фаз; A H о - мольная энтальпия реакции (7);

• 2)    уравнение массопереноса компонентов фазы Ф , связывающее удаление атомарного кислорода О с поверхности раздела фаз (в соответствие с химическими реакциями (7)) с подводом его к поверхности раздела из глубины рудной частицы:

Р ^Ф DО’-^с Ф ’ - [ * • R ( t ) - 0 ] +

+[ с0,-( t, R (t))-1] Vo’—1о = 0,(15)

Р ^Ф D Fe ’ - AF 1 1 ’ R ( t ) — 0 ] +

+ c 0e2+( t, R (t)) Vo’-1 о = 0,(16)

Р ^Ф D AAS⁴ t - R ( t ) - 0 ]+

+ с^Д t, R (t)) VO2-1 о = 0,(17)

где ν_i – молярная масса продукта i , умноженная на его стехиометрический коэффициент, в химической реакции образования продукта i ;

• 3)    уравнение массопереноса компонентов фазы " , связывающие подвод реагентов к поверхности раздела фаз с расходом их в соответствие с химической реакцией (7):

р" D'Co |сTo [t,R(t) + 0] + о r     L          J

V co ) I о = 0,   (18)

n

+ ! ( с 'о ( t , R ( t ) ) V o ’

I - —

k = 1

• 4)    уравнение химического равновесия химической реакции (7):

  -O — a Ф K ( T ) = 0, a CO

  
  
  
  

• 4.    Уравнение изменения размера частицы:

  dR dt

  
  

  = _р Ф ^Vo^{2 -} I ^о.

  
  
  
  

  5. Граничные условия:

  ST 1)     ( t ,0) = 0; d r	(21)
  дс Ф 2) -c^- ( t ,0) = 0, i = 1,..., n - 1; d r	(22)
  3) - ( t , » ) = - 0 ;	(23)
  4) c" ( t , w ) = c 0 " , i = 1,..., m - 1.	(24)

  
  

где ai – химическая активность компонента i ; K – константа равновесия химической реак- ции.

Обсуждение результатов

Полученная модель позволяет проводить расчет процесса образования и движения анионных вакансий в объёме комплексного оксида, рассматривая процесс восстановления как взаимодействие восстановителя не с молекулой оксида металла, а с анионом кислорода кристаллической решетки. При этом кислород переходит из решетки оксида (фазы Ф) в газовую фазу Ψ, оставляя после себя восстановительную вакансию, а продукт реакции CO2 удаляется из зоны реакции. Развитие этого процесса приводит к образованию потока восстановительных вакансий, который направлен от поверхности рудной частицы в её объем. В противоположном направлении происходит движение анионов кислорода. В предложенной модели химическая реакция на поверхности раздела фаз описывается уравнением (7). А движение восстановительных вакансий рассматривается как процесс уменьшение концентрации анионов кислорода O2– в объеме фазы Ф. Таким образом, зная изменение концентрации кислорода в любой точке рудной частицы в произвольный момент времени, можно судить о количестве восстановительных вакансий в данной части объема и во всей частице в целом. Процесс восстановления завершится, когда количество анионов кислорода фазы Ф уменьшится на значение, пропорциональное содержанию восстанавливаемого металла, в данном случае Fe.

Необходимо отметить, что данная модель не рассматривает аннигиляцию восстановительных вакансий с образованием металлической фазы, тем не менее из результатов экспериментов [13–15] можно сделать вывод о том, что выделение металлической фазы идет с минимальными энергетическими затратами и в тех частях объема рудных частиц, где происходит скопление восстановительных вакансий.

Заключение

Разработана математическая модель процесса образования и движения анионных вакансий в объёме комплексного оксида, позволяющая учитывать влияние основных физикохимических параметров на скорость появления и перемещения восстановительных вакансий, и, как следствие, на скорость процесса восстановления.