Математическая модель оценки эффективности использования земель сельскохозяйственного назначения

Важнейшая задача сельского хозяйства страны – обеспечение ее продовольственной безопасности. Основой сельскохозяйственного производства, призванного обеспечить эту безопасность, является земля, точнее земельные ресурсы сельскохозяйственного назначения. В настоящее время они стали предметом и средством труда в сельскохозяйственном производстве. К сожалению, в настоящее время, организация управления, различные подходы к рациональному использованию земельных ресурсов базируются на прошлом опыте, старых схемах и технологиях. Практически не применяются современные научные подходы, информационно-коммуникационные технологии, что недопустимо в стране, претендующей на роль ведущей, прогрессивной в мировом сообществе. В этом аспекте весьма актуальным представляется формирование концепции и соответствующей математической модели, позволяющей проводить современный качественный анализ эффективности использования земельных ресурсов, а также оптимизировать процесс выработки управленческих решений по такому использованию земельных ресурсов, которое обеспечивает эффективное развитие общества.

Целью любой отрасли является формирование устойчивого развития рассматриваемой сферы. В этом контексте представляется целесообразным рассматривать ее как социо-эколого-экономическую систему (СЭЭС).

Анализ эффективности использования земель сельскохозяйственного назначения.

Пусть имеется подсистема высокого уровня (ПВУ), которая содержит подсистемы низкого уровня (ПНУ). Для территориального объекта ПВУ может быть представлена муниципальным образованием, а ПНУ, соответственно предприятиями и индивидуальными предпринимателями; районом (ПНУ – муниципальные образования), регионом (ПНУ – районы), федеральным округом (ПНУ – регионы); РФ (ПНУ – федеральные округа).

Поставим задачу анализа: определить, насколько эффективно осуществляется комплексное (по трем осям, то есть вдоль экологического, социального и экономического направлений) управление в каждой подсистеме. Показатели эффективности по указанным осям должны быть нормализованы

(стандартизованы и приведены к безразмерному виду), а развитие должно удовлетворять условию:

,                                        (1)

51* + 51+5/ = (^)Г)2

где – «темп роста»; Т – планируемый период «роста» (постоянная времени);

• t, t0 – текущее время и начальный момент времени соответственно;– обобщенный нормализованный показатель природопользования, – обобщенный нормализованный показатель качества жизни населения, – обобщенный нормализованный экономический показатель. В случае равномерного роста вдоль осей нормализованные показатели должны быть равны между собой.

Определим абсолютные выходные параметры по 3-м осям (природной, социальной и экономической) в масштабе выбранной ПВУ.

Вдоль экологической оси в качестве показателя выберем почвенно-экологический индекс:

.                                                   (2)

Вдоль социальной оси остановимся на трех показателях (), характеризующих соответственно ожидаемую продолжительность жизни, уровень образования и ВВП на душу населения, занятого в сельском хозяйстве.

В направлении экономической оси остановимся на показателе, который является аналогом рентабельности продукции сельского хозяйства ().

зд

Далее нашей задачей является определение входных параметров по 3-м осям (социальной, экологической и экономической) в масштабе выбранной ПВУ.

Вдоль экологической оси такими показателями будут:

– плотность (объемная масса) почвы (в среднем для метрового слоя), г/см3; – максимально возможная плотность почв при их предельном уплотнении, г/см3; – «полезный» объем почвы в метровом слое; – дополнительно учитываемые свойства почв; – среднегодовая сумма активных температур выше 10оС; – коэффициент увлажнения (по Иванову); – поправка к коэффициенту увлажнения; – коэффициент континентальности; – итоговый агрохимический показатель.

Вдоль социальной оси такими входными параметрами могут быть социальные индикаторы , которые в 1980 году были утверждены ОСЭР [5] и выделены согласно системе «Основные показатели уровня жизни населения в условиях рыночной экономики», разработанной в Центре экономической конъюнктуры и прогнозирования при Министерстве экономики РФ и состоящей из 7 разделов и 39 частных показателей.

В направлении экономической оси можно включить: x3,1 – кадастровую стоимость земель сельхозназначения (руб/га); x3,2   – долю распаханности сельскохозяйственных угодий (%); x3,3 – количество среднегодовых работников (на 100 гектаров сельскохозяйственных угодий, чел.); x3,4 – годовой фонд оплаты труда 1-го работника (руб.); Х3 5 - стоимость основных производственных фондов сельскохозяйственного назначения (на 100 гектаров сельскохозяйственных угодий, тыс.руб.); x3,6 – стоимость основных производственных фондов сельскохозяйственного назначения (на 1-го среднегодового работника, тыс. руб.); x3,7 – количество физических тракторов (на 100 га пашни, шт.); x3,8 – издержки производства (на 100 гектаров сельскохозяйственных угодий, тыс.руб.); x3,9 – долю зерновых культур в площади пашни (%); x3,10 – долю зернобобовых

1$

культур в площади пашни (%); x 3_,11 – долю многолетних трав в площади пашни (%); x 3_,12 – долю чистых паров в площади пашни (%); x 3_,13 – поголовье КРС (на 100 га сельскохозяйственных

■11   л139:

угодий, гол.); x 3_,14 – внесение минеральных удобрений (на 1 га пашни, кг); x 3_,15 – балл бонитета.

Предположим, что связь между выходными и входными параметрами имеет линейный характер [1] (за исключением экологической оси):

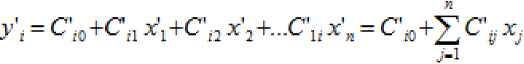
,                         (3)

гд е – i-тый выходной параметр (наблюдаемое явление); – входные параметры (условия, при которых наблюдается явление), выраженные в натуральных или стоимостных единицах измерения.

В случае рассмотрения экологической оси будем использовать соотношение:

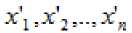
ПЭ_И =12.5 - (2 - Р) - 77- Дс - У Л(> 10°) ■ ——— - А

А’А'+ЮО

Далее сформируем базу статистических данных (входные и выходные параметры) для всех ПНУ с использованием статистических справочников, бюллетеней или

воспользовавшись электронными ресурсами.

Посредством минимизации квадрата разности между фактическими данными и данными, рассчитанными

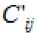
по линейной модели, определяем «весовые» коэффициенты [3]:

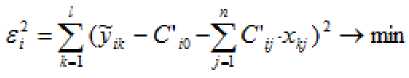
Здесь – фактические значения результативного признака l – число наблюдений (количество взятых в рассмотрение единиц совокупности), i=1..m – индекс результативного показателя.

у „ Для анализа чувствительности воздействия результата к факторным признакам и с целью сравнения влияния на зависимую переменную объясняющих переменных, когда они представлены в

разных единицах измерения, возникает необходимость использования безразмерных величин. Тогда в

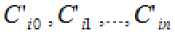
уравнении (3) вместо необходимо использовать стандартизованные коэффициенты регрессии и стандартизованные переменные:

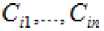
где

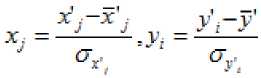
соответствующие среднеквадратические отклонения, а

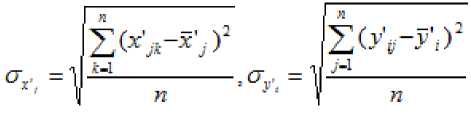
.                                                      (8)

Примечание. Для количества наблюдений меньшего 30 в знаменателе (7) должно быть выражение ( n-1) .

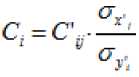
Стандартизованный коэффициент регрессии показывает, на сколько изменится в среднем результативный показатель при увеличении одного факторного признака на .

Таким образом, приходим к следующему виду регрессионной модели [2]:

Оставляем в модели только существенные входные параметры посредством использования ^^г, факторного анализа и определения частного F -критерия Фишера, который оценивает статистическую значимость присутствия каждого из факторов в уравнении. В общем виде для фактора x _i частный F — критерий определится как

Оценка значимости коэффициентов чистой регрессии с помощью t-критерия Стьюдента сводится к вычислению значения

X

,                                      (11)

<7 ■

~ ' где – средняя квадратичная ошибка коэффициента регрессии, – коэффициенты уравнения регрессии в форме (3). Если рассматривается только один результативный показатель , то индекс 1 н         можно опустить.

y, = C._nx +С^ +...C;_x_n = У (Lx,

Величина может быть определена по следующей формуле:

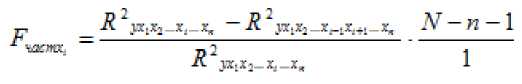
— индексы множественной корреляции.

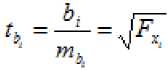
В результате описанных операций получаем т.н.

«модель нормативов» по природной, социальной и экономической осям. Представляет интерес знание, насколько полно оставленные нами для рассмотрения входные параметры «представляют» выходные параметры. Такое знание достигается

посредством вычисления коэффициента детерминации R ² , выявляющего значимость уравнения множественной регрессии.

Подставляя в модель нормативов фактические входные параметры конкретной ПНУ, определяем выходные параметры ПНУ, являющиеся т.н. «нормативными» значениями (далее

– «нормативами») для данного ПНУ.

V

Далее проверяем на мультиколлинеарность выходные параметры ПНУ (фактические и нормативные), отсекая менее существенные.

Проверка факторов на мультиколлинеарность может быть проведена методом испытания гипотезы

ox -^-R^x^-x. ^N-n-1

о независимости переменных Но : Det =1 [6]. величина

Доказано, что

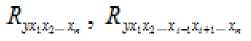
имеет приближенное распределение с степенями свободы. Если фактическое значение превосходит табличное (критическое) , то гипотеза Но отклоняется. Это означает, что , недиагональные ненулевые коэффициенты корреляции

указывают на коллинеарность факторов. Мультиколлинеарность считается доказанной.

Далее проводим операцию формирования единственного выходного параметра по каждой из осей

2                     отдельно для  фактических и нормативных значений. Если под bV-l--(2w + 5) lg(Z>^|J?|)]   компонентами   вектора понимать значение выбранной единицы совокупности,   представленной в косоугольном базисе, который формируется посредством усреднения (простого среднего /3 арифметического) по всей совокупности, то длиной вектора можно считать следующее соотношение:

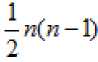
где

z1

Здесь R – корреляционная матрица, – парные коэффициенты корреляции, определяемые по формуле

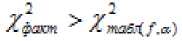
где n – число наблюдений (единиц совокупности);

– индекс соответствующего номер наблюдения (индекс

компонента вектора ; m – число компонент, – Det|£|#l соответствующей единицы совокупности).

При определении фактического значения длины показателя в качестве берутся y = {y1: y2_, yje? фактические значения результативного признака для i-того компонента, k-той единицы совокупности. Обозначим соответствующее значение где k – индекс выбранной единицы совокупности.

Для вычисления нормативного значения показателя, воспользуемся соотношением

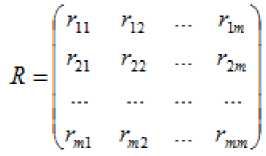
,                     (18)

где m – число результативных признаков; n – число факторных признаков; i – индекс i-того результативного признака; j – индекс j-того результативного признака; p – индекс p-того факторного признака; q – индекс q-того факторного признака; k – индекс рассматриваемой единицы совокупности; – r^ парный коэффициент корреляции между i-тым и j-тым результативным признаком; – весовой коэффициент   между i-тым результативным и p-тым факторным признаками; – весовой

я

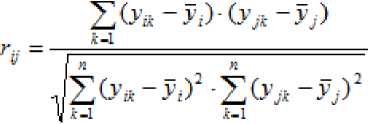
коэффициент между j -тым результативным и q -тым факторным признаками; – фактическое значение стандартизованного p -того факторного признака для k -той единицы совокупности; – фактическое значение стандартизованного q -того факторного признака для k -той единицы совокупности.

Парные коэффициенты корреляции определяются по формуле:

LJ = l..m   ,                (19)

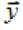
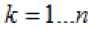
n – число наблюдений, l – число факторных признаков.

Далее находим отношение реальных (фактических) выходных данных ПНУ с нормативами для данной ПНУ по каждой из осей

JM .                                (22)

Здесь – значение i -того обобщающего показателя (здесь под i понимается направление в ПСЭ-=|y| пространстве, для простоты в соотношениях (17)-(18) этот индекс опущен, для k -той единицы совокупности; , – фактическое и «нормативное» значения обобщающих

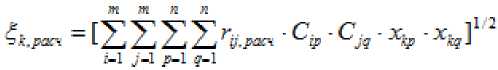
— если хоть один из трех выходных дифференциальные рекомендации для

показателей соответственно.

Результаты сравнения должны быть подвергнуты логической обработке по алгоритму:

параметров ПНУ меньше норматива, то формируются данной ПНУ, как достичь норматива, перераспределив статьи расходов по входным параметрам по каждой из трех осей;

у

— если все три выходных параметра ПНУ выше норматива, то оценивается динамика «длины» вектора: при положительной динамике делается вывод о рациональном развитии субъекта, при отрицательной – выявляются причины, приведшие ПНУ к данному состоянию (рис.1).

■кд

Рис. 1. Принятие решений в зависимости от значения обобщенного показателя эффективности , t – время, A – полуразмах поля допуска, формируемый в зависимости от количества групп (формула Стерджесса).

В зависимости от значения решение может быть реализовано по одному из трех возможных путей, указанных на схеме.

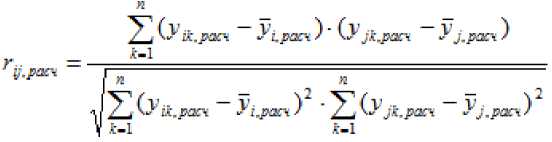
Синтез управленческих решений

Дифференциальные рекомендации по конкретному ПНУ формируются посредством оптимизации изменения входных параметров ПНУ по критерию приближения фактических результативных признаков нормативному значению [4].

• - ik.pacx ~ ^ Cp ' ^XV Для этого используем соотношение:

,                           (23)

v = — (V УС-л^,)

• ^^ ^и i-1 UI          где m – число результативных признаков, n – число факторных признаков, i –

индекс i -того результативного признака, j – индекс j -того результативного признака, p – индекс p -того факторного признака, q – индекс q -того факторного признака, ь     5"ик.фахт   k – индекс рассматриваемой единицы совокупности, – парный коэффициент корреляции

• -^   Л..      между i -тым и j -тым результативным признаком, – «весовой» коэффициент между i -тым

результативным и p-тым факторным признаками, – «весовой» коэффициент между j-тым результативным и q-тым факторным признаками, – фактическое значение стандартизованного p-5ti того факторного признака для k-той  единицы совокупности, – фактическое значение стандартизованного q-того факторного признака для k-той единицы совокупности, – акселератор p-^        того факторного признака для k-той единицы совокупности, – акселератор q-того факторного

признака для k -той единицы совокупности.

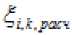
Затем вычислим частные производные по параметрам – акселераторам – и выделим из них максимальное значение. После некоторых преобразований получим:

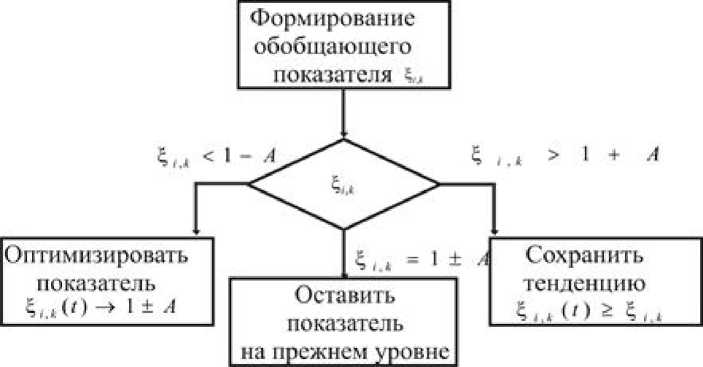
. (24)

Здесь i,j,p – индексы суммирования, s – индекс s -того акселератора, k – индекс рассматриваемой единицы совокупности, по которому берется частная производная. Определим s -тый индекс из условия:

. (25)

Определив s-тый индекс, можно переходить к определению s-того акселератора, приняв, что на первом шаге все остальные значения акселераторов равны единице.

Проранжировав ряд частных производных по условию (24), найдем следующий индекс s . Используя X описанную методику, найдем последующие значения с учетом найденного на предыдущем шаге значения акселератора. Процесс продолжается до тех пор, пока не будет выполнено равенство , после чего процедура поиска завершается.

Поиск есть не что иное, как выявление причин, вызвавших «недотягивание» результатов деятельности л = {УУУУг -С -С .—^—^-l1'2

•=t.*®*   l-2-i 2-i 2-i 2-i У У jq 1Z         J i-1 y-1 ?-l g-1              ^ ^kq

производителей сельскохозяйственной продукции ПНУ до «нормативных» параметров. Производится оценка степени потерь при использовании s-того фактора.

Также очевидно, что потери – это излишние затраты на единицу используемого факторного признака. Следовательно, акселератор показывает, как необходимо сократить (увеличить при >1) расходы на s -тый факторный признак для достижения «нормативных» показателей. Это и определяет сущность

C, практических рекомендаций для k -той единицы совокупности.

Полученные показатели могут быть использованы для разработки управленческих решений на всех уровнях в соответствии с фрактальным подходом.

По результатам могут быть построены графики с результатами отношения выходных параметров ПНУ к нормативам (меньше 1, равно 1, больше 1), а также картограммы территории ПНУ с нанесением показателей сравнения по каждой из трех осей. Блок-схема алгоритма, реализующего описанную математическую модель и использованного при анализе эффективности использования земель сельскохозяйственного назначения в Тульской области, а также синтезе управленческих решений для некоторых районов Тульской области, представлена на рис.2.

В качестве примера приведем результаты расчета обобщенного показателя вдоль экономической оси и оптимизацию входных параметров с целью разработки практических рекомендаций для подсистем Тульской области, занимающихся сельскохозяйственным производством.

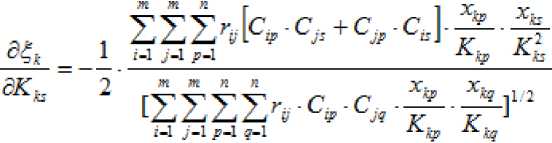
На рис.3 представлены приведенные значения обобщенного показателя эффективности вдоль экономической оси.

Рассмотрим Воловский район, который имеет положительную рентабельность (1,7% в фактических значениях, -0,038 в

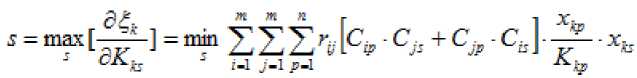
стандартизованных), соответствующее значение составляет 0,840 (норма – 0,713, факт – 0,598) при требуемом «нормативе» 1.

K-^ Следовательно, для того чтобы фактическое значение и «нормативное» значение совпадали, после пересчета в стандартизованные переменные необходимо, чтобы y ₅ф_акт =0,496 при имеющемся л. .   = Л      значении y ₅ф_акт =-0,038 .

Используя формулы (23)-(25), можно определить направления оптимизации ^L результативного признака.

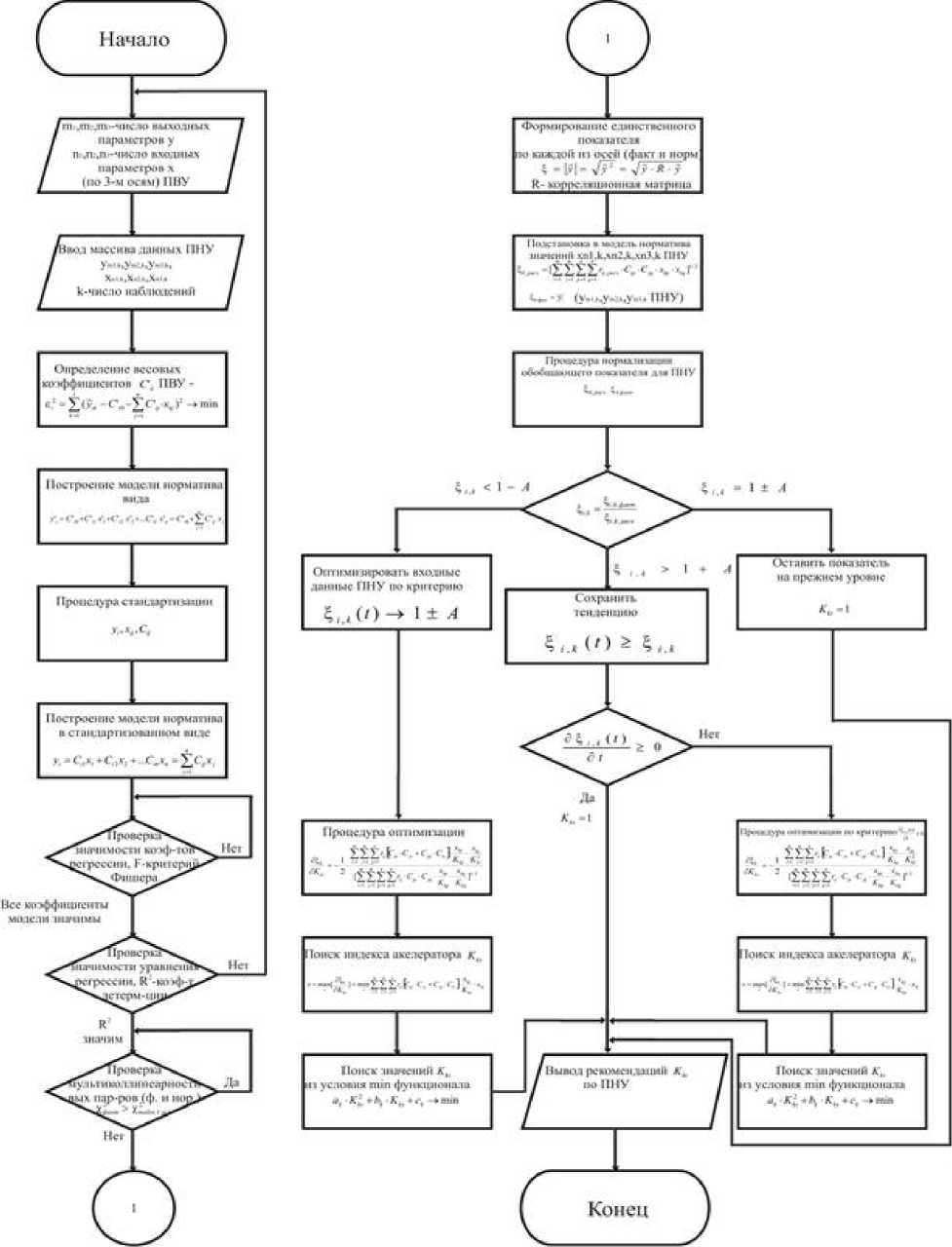
Рис.2. Блок-схема алгоритма, эффективности использования решений.

реализующего описанную математическую модель для анализа земель сельскохозяйственного назначения и синтеза управленческих

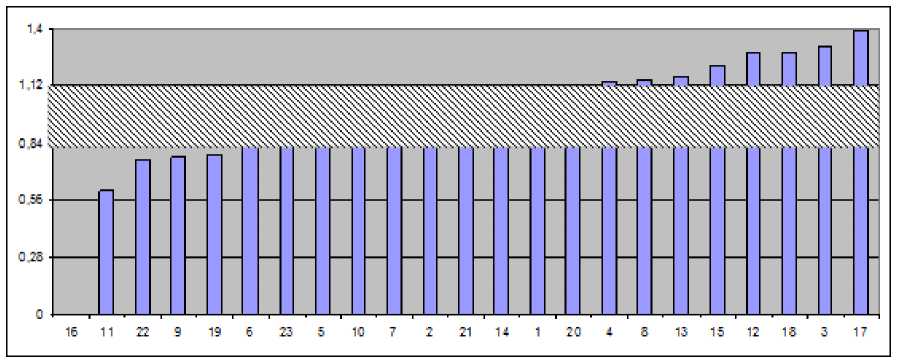
Рис. 3. Значения показателя экономической эффективности по районам (в долях). Заштрихованная область показывает, что значение показателя находится в допустимых пределах (в данном случае значение 1 показывает среднюю по Тульской области рентабельность, которая составляет 3,0%). По оси абсцисс – номера районов: 1- Алексинский район, 2- Арсеньевский район, 3 – Белевский район, 4 – Богородицкий район, 5 – Веневский район, 6 – Воловский район, 7- Дубенский район, 8 – Ефремовский район, 9 – Заокский район, 10 – Каменский район, 11 – Кимовский район, 12 – Киреевский район, 13 – Куркинский район, 14 – Ленинский район, 15 – Новомосковский район, 16 – Одоевский район, 17 – Плавский район, 18- Суворовский район, 19 – Тепло-Огаревский район, 20 – Узловский район, 21 – Чернский район, 22 – Щекинский район, 23 – Ясногорский район. По данным Федеральной службы государственной статистики [7].

Пусть результат хозяйственной деятельности представляется в виде функции (стандартизованная модель):

y 5 =1,074x i(5) -1,301X 9(5) -0,440x i6(5) +0,931X 6(5)

Здесь x i(5) — кадастровая стоимость земель с/х назначения , X 95 — доля зерновых культур в площади пашни, x i6(4) - затраты на зерновые, X 6(5) - затраты на запчасти и ремонт.

Тогда будем иметь:

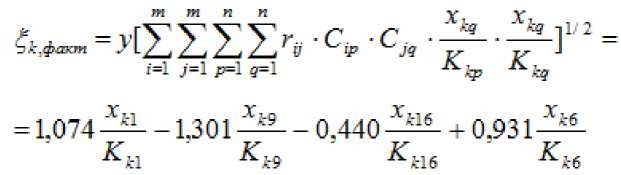
,                       (28)

,                     (27)

здесь к =6 (индекс Воловского района), К ^ -соответствующие акселераторы.

Подставив конкретные значения факторных признаков , получим:

Далее необходимо, чтобы «наискорейшим» образом. Следовательно, найдем частные производные

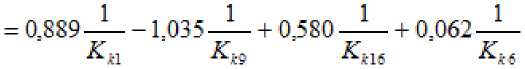
по каждому из параметров К ^ и определим направление, в котором наблюдается «наискорейший» рост функции (8.13).

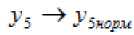
.           (29)

Проранжировав соответствующие индексы, найдем:

То есть, для разработки предложений по повышению экономической эффективности использования земельных ресурсов необходимо последовательно рассмотреть влияние: кадастровой стоимости земель

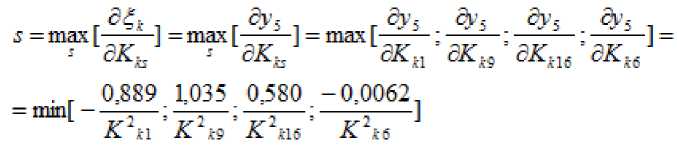
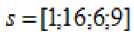
с/х назначения; затрат на зерновые; затрат на запчасти и ремонт; доли зерновых в площади пашни. Изучая первый показатель, приходим к следующему соотношению:

.                                    (33)

0.038 = 0.889 —--1.0351 + 0.580-+0.062"                                             1                1                1

Значение показателя свидетельствует о том, что необходимо в 2,5 раза улучшить использование земли посредством оптимизации факторов, входящих в

। формулу расчета кадастровой стоимости земли. То есть расчетная кадастровая OJ55 =0,889-^- стоимость земли составляет 18515 руб., а реальная 7385 руб. Приведение реальной ti    стоимости к расчетной проведем на основании следующих рассуждений.

An = 2=507

An = 2=507

Используя дополнительные данные об урожайности зерновых культур в Воловском районе, убедимся, что расчетная продуктивность выше фактической (урожайность на 9,43% ниже «нормативной» в абсолютных величинах). Из таблицы очевиден недостаток внесения минеральных удобрений в почву (соответствующий показатель x2(2)= –0,839 отрицателен). Тогда для достижения «нормативной» урожайности необходимо увеличить внесение минеральных удобрений на 71,7%, рассчитав ее по модели урожайности (в предположении, что все остальные показатели неизменны):

,                            (34)

Дхд2) = [1/(1 - 0,943)]/ 0,642-100*? 6 = 71,7%

Тогда значение реальной стоимости земли увеличится на

10,4% и значение акселератора при такой процедуре станет равным .

£н = 1,104

Сравнив полученное содержание минеральных веществ с оптимальными (оптимум по содержанию подвижного фосфора и калия (по Чирикову) составляет соответственно 17,5 мг/100 г почвы и 15,0 мг/100 г почвы соответственно [68]), можно оценить возможность дальнейшего увеличения, что приведет к увеличению величины акселератора. Анализируя каждый из факторов, максимизируем показатель так, чтобы

.                                              (35)

£tl <2=507

В случае процедура оптимизации прекращается, иначе переходим к следующему по важности признаку ().

£п = 2=507

Пусть в результате первого шага оптимизации акселератор . Тогда (27) преобразуется к виду:

TV

,                       (36)

^tl =1700 и, приравнивая , единице, получим следующее соотношение

v -0.889^— -1.035 — + 0.580-^— + 0.062 —

• ⁵    "    1700   -            - К_И6 "    ^_t6

i9 Значение показателя свидетельствует о том, что необходимо примерно в 1,4 раза увеличить затраты на производство зерновых культур посредством оптимизации факторов, входящих в соответствующую формулу расчета. Основными статьями затрат являются затраты на покупку семян, то есть очевидным является факт приобретения семян зерновых высокого качества.

Последовательно рассматривая оставшиеся показатели, можно обеспечить достижение

0,038 = 0,889     -1.035 - + 0.580 — + 0,062 -

'         "     1,700 "     1    " ГН6 "     1

«нормативного» значения показателя.

На данном примере была показана технология синтеза обоснованных оптимальных решений, количественно и качественно определены

основные пути повышения экономической эффективности использования земельных

0.412 = 0.580 ресурсов.

Заключение

£i6 =1,409 В результате проведенного исследования была представлена методика построения математической модели оценки эффективности использования земельных ресурсов

Г -1 4AQ сельскохозяйственного назначения. Оценка проводится в контексте социо-эколого-A.r.g — 1.4Uy экономических систем, где по каждому направлению (социальному, экологическому и экономическому) формируется обобщенный нормированный показатель, позволяющий сравнить эффективность развития по каждой из осей.

Каждый из показателей эффективности есть отношение фактического и нормативного значений, которые определяются совокупностью показателей по каждой из осей, объединенных по разработанной методике.

Норматив определяется на основании построенной модели с помощью корреляционно-регрессионного и факторного анализа.

В рамках проведенного исследования были рассмотрены вопросы, связанные с повышением эффективности использования земель сельскохозяйственного назначения с помощью предложенной авторами методики оптимизации процесса управления сельскохозяйственным производством и принятия обоснованных решений (на примере Тульской области).

В современном обществе все большую актуальность приобретает внедрение информационнокоммуникационных и инновационных технологий, а также проблема рационального использования интеллектуального потенциала в процессе существования и работы различных подсистем. Применительно к сельскохозяйственной отрасли находится в стадии разработки предложенный авторами программный комплекс оптимизации принятия управленческих решений, что существенно упрощает процедуру анализа и повышения эффективности использования земельных ресурсов сельскохозяйственного назначения.