Математическая модель определения начального участка гетерогенного факела и ее адаптация

В теории горения энергетических топлив общепризнанными являются математические модели с критическими условиями самовоспламенения в нестационарной и стационарной постановке, связанные с работами советских академиков Я.Б. Зельдовича и Н.Н. Семенова [1, 2]. Эти модели построены на анализе основных соотношений тепло-переноса в объеме предварительно перемешанных компонентов горения при различных условиях адаптации к реальным схемам. Причем нестационарная теория рассматривает распространение пламени в закрытом объеме, что соответствует в основном нештатным ситуациям в энергетике, а стационарную теорию можно применить к устойчивому процессу горения в движущейся смеси компонентов горения. Обе теории содержат рекомендации по управлению процессом горения при воспламенении от внешнего источника. Изложенный ниже материал дополняет ряд данных по математическому описанию различных элементов процесса горения топлива, начиная с участка, где смесь нагревается до условий воспламенения.

1. Постановка задачи.Процессы в начальном участке факела

Недостаточная изученность вопросов горения топлива связана со сложностью процесса, который основан на фундаментальных законах переноса субстанций – теплоты, массы, импульса с включением основных законов химической кинетики. Воспламенение, переходящее в устойчивое горение, возможно только при благоприятном сочетании факторов химической, аэромеханической и тепловой природы. Это находит отражение в физических механизмах смесеобразования, зажигания и самовоспламенения при условии получения смеси в пределах «горючего состава» и наличии локальных актов горения с тепловым эффектом, достаточным для инициирования и распространения горения на весь объем смеси. С точки зрения технологии горения это означает, что смесь находится в интервале воспламенения, между «нижним» и «верхним» пределами, скорость потока сопоставима со скоростью распространения пламени, энтальпия горения достаточна для поддержания процесса.

При классификации способов воспламенения горючих смесей с учетом классических методов можно условно выделить три схемы:

– нагрев объема смеси до температуры самовоспламенения t св ;

– зажигание от контакта с пламенем, имеющим температуру t пл >  t св , но при этом температура смеси может быть ниже t св ;

– зажигание от нагретой твердой поверхности при t _пов >  t _св.

В основе всех трех схем лежит не сформулированное в явном виде допущение, что горючая смесь находится в пределах нижнего воспламенения, соответствующего «бедным» смесям, и верхнего, соответствующего «богатым» смесям. На основе анализа теплофизических соотношений можно полагать, что выход за верхний предел воспламенения связан с устойчивостью горящего факела, а для задачи определения начального участка определяющим является нижний предел воспламенения. При этом существенны схемы с зажиганием, но возможна и схема горения предварительно перемешанных компонентов горения, тогда определяющей становится схема с нагревом объема смеси до температуры t _св. Возможны и более сложные схемы, которые можно анализировать по сформулированным выше принципам и схемам.

При определении зависимости температуры факела от его длины Т ф ( L ф ) посредством предложенной ранее интегральной функции тепловыделения Ф( L ф ) начало горящего гетерогенного факела размещается в плоскость воспламенения L ф = 0, но эта плоскость отстоит от выходного сопла горелочного устройства на расстоянии l _н, м. Таким образом, для согласования геометрических размеров факела с функцией тепловыделения необходимо определить протяженность начального участка и сформулировать систему физико-математических соотношений для определения факторов, влияющих на l _н, что и является задачей настоящей работы.

Процесс термического разложения вещества твердого топлива имеет сложную природу, зависящую от исходного состояния топлива и условий нагрева; этот процесс можно разделить на три стадии – бертинирование (0–300 °С), полукоксование (300–600 °С) и коксование (600–1100 °С). На рис. 1 изображены термо-гравиметрические кривые, построенные по данным [3, 4], где показано изменение выхода продуктов термической деструкции природного твердого топлива, относящегося к категории гумолитов, в процентах на сухую беззольную массу.

В первой стадии выделяется небольшое количество газообразных продуктов разложения ~ 3,0 % от исходной массы, с низкой теплотой сгорания. При определении начального участка факела эту стадию можно не учитывать, тем более, что продукты газификации в первой стадии учитываются в составе второй стадии. Температурные функции выделения трех компонентов летучих веществ – газовой фазы V _г ^г _аз , пирогенетической воды V _г ^г _аз и смолистых веществ V _г ^г _аз на горючую

(сухую беззольную) массу можно описать следующими аппроксимациями:

Vг = 3,0 + 6,17-10-2 AZ;(1)

газ

VnrB = 3,0 +1,5-10"2AZ;(2)

Vm = 3,7 -10-2 AZ.(3)

Начальный участок факельного континуума протяженностью l _н, м, от выхода смеси из горелочного устройства до плоскости воспламенения определяет стабильность процесса горения и частично его эффективность; на этом участке всем явлениям переноса субстанций свойственна четко выраженная трехмерная пространственная структура.

Применение концепции факельного континуума [3] позволяет рассматривать задачу в двух измерениях – с учетом продольной l и поперечной r координат. Причем теплофизические свойства факельной среды считаются постоянными в направлении r , ступенчато изменяющиеся к свойствам топочного газа на границе факела. Задача для начального участка включает не только определение его длины l _н , но и определение возможности применения управляющих воздействий в направлении изменения основных его характеристик.

При определении начального участка гетерогенного факела существенную роль играет динамика выхода летучих веществ из топливных частиц при нагреве. Суммарный эффект выхода летучих веществ определяется сложением уравнений (1)–(3), а перевод в измерение в процентах от рабочей смеси – умножением на (100 – А ^р – W ^p)/100, в результате получается уравнение

V p = 3,480 + 6,595 - 10 ^{- 2} A Z                  (4)

или в массовых долях

V ^p = 0,0348 + 0,6595 - 10 — ³ A Z .              (5)

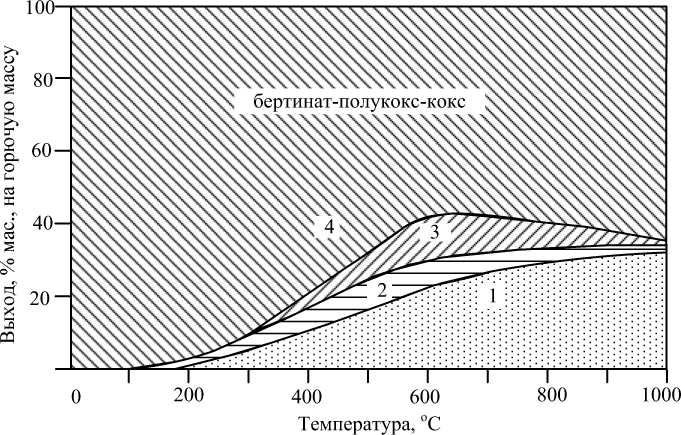
Рис. 1. Выход продуктов термического разложения в зависимости от температуры: 1 – газ; 2 – пирогенетическая вода; 3 – смола; 4 – твердый остаток

Уравнения (4)–(5) связывают количество выделяемых летучих веществ с уровнем нагрева частиц топлива в интервале температур 300–600 °С, причем Δ t = t – 300. При получении уравнений (4)–(5) приняты средние значения балластных составляющих бурого угля А ^р = 7,0 %, W ^p = 35,0 %.

При выборе алгоритма определения начального участка факела от выхода дисперсного потока из горелочного устройства до начала воспламенения l _н необходимо выделить несколько схем по принципу учета влияния определяющих факторов, на основе идентификации которых разрабатываются математические модели расчета l н . Предлагается следующая схема классификации:

– расчет на основе определения температуры интенсивного выхода летучих веществ t инт , которая косвенно соответствует температуре воспламенения;

– расчет на основе определения концентрации летучих веществ в смеси с воздухом μ_см, которая формируется динамикой нагрева топливных частиц и соответствует нижнему пределу воспламенения газо-воздушной смеси μ_см = μ_н;

– применение стандартной методики расчета взрывобезопасных концентраций топливной пыли в системе подготовки и транспорта топливной пыли [3];

– использование экспериментальных данных по времени воспламенения летучих веществ в неподвижном окислителе [4];

– использование данных, полученных на экспериментальной установке по сжиганию пыли каменных углей месторождения в Питтсбурге [5].

Все перечисленные алгоритмы относятся к аналитическим методам; возможен также численный расчет всех параметров факела, например, с помощью пакета ANSYS. Выбор того, или иного метода зависит от цели исследования и имеющимся в распоряжении исследователя теоретическим или экспериментальным материалом. В настоящей статье ставится задача сопоставить пять перечисленных аналитических методов с целью выработки достоверных выводов.

• 2.    Математическая модель определения lн на основе расчета tт

Для учета динамики нагрева частиц топлива размером δ, м, можно применить критериальное уравнение для термически тонких тел

In 0 = - 3Bi • Fo, (6) где Bi = αδ/λ – число Био, Fo = a τ/δ² – число Фурье, Θ = θ л /θ 0 – безразмерная температура топливной частицы. На рис. 2 представлена номограмма, построенная по уравнению (6), которая позволяет быстро определить безразмерное время процесса нагрева Fo для частиц размером δ, причем область больших значений числа Fo > 10 относится к частицам меньшего размера δ .

Зависимость (6) преобразуется с учетом коэффициентов массивности m = 1,003–1,067 для самых мелких и самых крупных частиц топливной пыли и формы ζ = 3,0:

т = [5р cm/ ( 2 a£ ) ] ln ( 9 q /0 л ) , (7) где θ₀ = t _т – t _нач – начальный температурный перепад; θ_л = t _т – t _в – температурный перепад соответствующий выделению летучих веществ в количестве, достаточном для воспламенения при нижнем

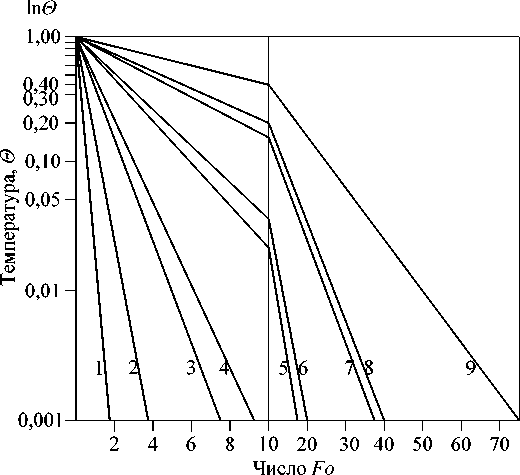
Рис. 2. Номограмма по определению безразмерного времени процесса нагрева Fo для частиц размером δ по числу Bi : 1 – Bi = 0,18; 2 – Bi = 0,091; 3 – Bi = 0,045; 4 – Bi = 0,0364; 5 – Bi = 0,0182;

6 – Bi = 0,01164; 7 – Bi = 0,0091; 8 – Bi = 0,0082; 9 – Bi = 0,0045

пределе μн; также tт, tнач, tв – температура топочных газов, начальная температура топливных частиц и температура воспламенения летучих веществ соответственно, °С. Температуре tт присваивается смысл такого нагрева топливной пыли, который приводит к выделению летучих веществ в количе- стве, достаточном для воспламенения.

Применение рис. 2 ограничено условиями внешнего нагрева частиц пыли с интенсивностью результирующей теплоотдачи α, Вт/м2·К. После воспламенения результирующий тепловой поток определяется с учетом собственного излучения частицы.

Выделение летучих веществ и их смешение с воздухом в количестве V _α = α_в V ₀, м³/кг топлива, приводит к образованию газо-воздушной смеси, состав которой можно определить в соответствии с (5) в массовых долях по формуле

Ц см = V p/ ( V p +Р в V a ) . (8)

Этой концентрации газо-воздушной смеси со- ответствует динамика выделения летучих веществ, определяемая с учетом (5) по формуле

( 0,0348 + 0,6595 •Ю^{- 3} A t )

Цсм =     -------------------з-------;

( 0,0348 + 0,6595 • 10 ^{- 3} A t + р _в V _a)

при получении обратной функции

At = цСм (0,0348 + РвVJ-0,0348(10)

0,6595 •Ю-3 (1 -Цсм)

При достижении газо-воздушной смесью концентрации, соответствующей нижнему пределу воспламенения μсм = μвс, температура соответствует температурному перепаду воспламенения

Δ t вс = t вс – 300, а θ л = θ вс = t т – Δ t вс и с заменой концентрации и температуры на таковые при воспламенении можно в (7) подставить вместо θ_л = θ_вс, что дает возможность определить время воспламенения при m ≈ 1,0 и ζ = 3,0:

Т вс =[ 0,4 •Ю ⁶ 5/ба] ln ( 9 0 /9 вс ) , (11) где δ – размер топливной частицы, м; α – коэффициент суммарной теплоотдачи на поверхность частицы топливной пыли, Вт/м²·К, θ₀ = t _т – t _нач.

С учетом (6), (11), а также аэромеханического коэффициента увеличения поперечного сечения факела kF = (1 + 0,21lн /d0)–2, можно получить lн = w kF Твс (12)

и далее

1 3 + 9,5238 dJ 2 + 11,3379 d ₀ ³ L = 56,44 w_od _o2/a, (13) н 0н 0н 0 0

где принято: t _т = 1220 °С, t _нач = 20 °С, t _вс = 650 °С.

Уравнение (13) можно решить методом Кардано или численно-графическим методом с помощью построения соответствующего графика. На рис. 3 изображен график, который позволяет определить l н в соответствии с уравнением (13), значения левой части которого нанесены на ось ординат в функции искомого l н , а значения правой части уравнения (13), которые не зависят от l н , соответствуют абсциссе.

График (см. рис. 3) построен для значения d ₀ = 0,20 м, если на практике определяется длина начального участка для горелочного устройства с диаметром выходного сопла d _пр, отличным от d ₀, к определенному по графику значению l _н^гр вводится поправка, равная 4,375 d ф , то есть, l _н^ф = 4,375 d ф · l _н^гр. Если значение правой части уравнения (13) не совпадает с нанесенными на линии числами, то можно

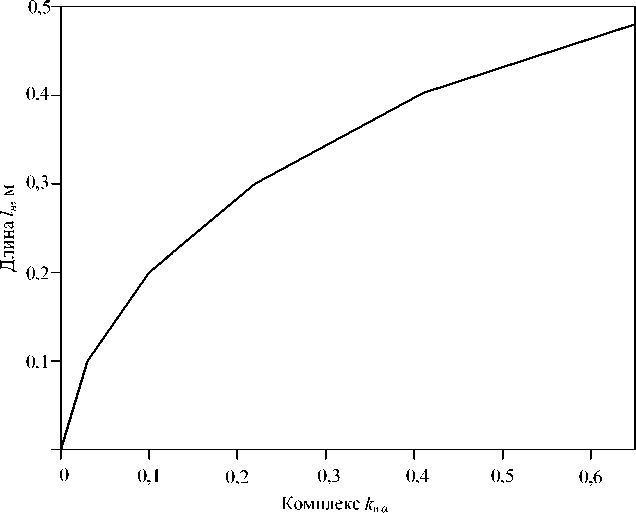
Рис. 3. График для определения начального участка факела l _н по значению комплекса k w α = 2,2576 w 0 /α

применить интерполяцию, или рассчитать индивидуальное значение числа правой части для конкретных условий. При определении l н для тестовых значений w 0 = 10 м/с, d 0 = 0,20 м, α = 150 Вт/м²К получаем по графику l н = 0,212 м, что удовлетворительно согласуется с экспериментальными данными.

• 3.    Математическая модель определения lн на основе расчета μн

  Температура начала выхода летучих веществ зависит от степени метаморфизма исходного угля и изменяется от 170 °С для бурых углей до 380 °С для антрацита [4]; завершается выход летучих веществ при температуре 800–1000 °С. Приняв, как и ранее, интервал 300–600 °С основным для определения состава газовой фазы и пределов воспламенения, можно отметить, согласно рис. 1, что процесс нагрева частиц угольной пыли в этом интервале температур аналогичен начальному периоду нагрева угольной шихты при получении кокса.

• 4.    Адаптация стандартной методики определения взрывобезопасных концентраций топливной пыли

Основные технологические отличия в рамках поставленной задачи заключаются в следующем: состав газовой фазы при факельном сжигании твердого топлива соответствует динамике процесса нагрева частиц топлива, а состав первичного коксового газа изменяется при смешении в коллекторах газовых объемов с разных ячеек коксовой батареи и в процессе очистки от каменноугольной смолы и сопутствующих веществ. Поэтому справочные данные по пределам воспламенения для промышленного коксового газа должны быть ниже таковых для газовой фазы в факеле угольной пыли.

Пределы воспламенения смесей различных газов с окислителем по методике ЭНИН [5] можно определить, поделив сумму объемных концентраций индивидуальных газов на сумму отношений этих концентраций к пределам воспламенения индивидуальных газов. При разбавлении газовой смеси инертными примесями (N 2 , CO 2 ) расчет пределов воспламенения ведется по той же методике, но с учетом содержания инертных газов, причем горючие компоненты газовой смеси группируются с балластом пропорционально объемному содержанию горючего компонента.

Изменение пределов воспламенения смеси с инертными компонентами определяется по экспериментальным графикам ЭНИН [5]. Как показывают расчеты пределов воспламенения по методике ЭНИН, при переходе от промышленного коксового газа к факельному газу, который считается аналогичным первичному коксовому газу, нижний предел воспламенения μн в объемных процентах возрастает в 1,352 раза – от 5,70 до 7,71 %, а верхний предел воспламенения снижается в 0,816 раз – от 29,4 до 24,0 %. Перевод объемных процентов в массовые доли производится согласно простой зависимости μн = 7,71·ρг /(100·ρсм) = 0,07. При этом значении μн по формуле (10) получаем Δtвс = 570 °С и θвс = 1220 – 570 = 650 °С и соответствие с предыдущим расчетом, отличие заключается в определении температуры воспламенения через расчет нижнего предела воспламенения по данным ЭНИН.

В теплоэнергетике принято определять взрывоопасность пыли природных твердых топлив при наличии источника зажигания, которая зависит от состава топлив, химической активности компонентов летучих веществ, содержания кокса золы. Для оценки взрывоопасности природных твердых топлив используется критерий взрываемости K т , определяемый расчетным путем как отношение объема летучих веществ на сухую массу топлива V ^с к нижнему пределу воспламеняемости с учетом нелетучего остатка (кокса и золы) μ^н_лб / K _т = V ^c/μ^н_лб. По величине K _т энергетические твердые топлива разделены на четыре группы от K _т ≤ 1,0 до K _т ≥ 3,5.

Методика определения нижнего предела воспламенения основана на расчете теплоты сгорания летучих веществ на сухую беззольную массу, которая также корректируется с учетом кислорода топлива и называется «кислородной массой». Теплота сгорания летучих веществ определяется по разности между теплотой сгорания исходного топлива и теплотой сгорания углерода кокса.

Нижний предел воспламенения определяется в двух вариантах: первый расчет достаточно обоснован, так как μнл определяется делением экспериментальной константы 1,26·105 на теплоту сгорания летучих веществ. Второй расчет производится с учетом твердого нелетучего остатка (кокса и золы), что вызывает сомнения, так как оставшийся после выхода летучих веществ твердый остаток почти не влияет на воспламенение смеси летучих веществ с воздухом.

Эти данные не предоставляют возможности использовать определенные в [6] K _т для расчета начального участка факела, так как в основе определения критерия взрываемости лежит не расчет нижнего предела воспламенения смеси летучих веществ с воздухом, а расчет μ^н лб , что не соответствует физико-химической природе воспламенения.

Но применить результаты работы [6] можно в отношении μ^н л , но при этом необходимо произвести пересчет с сухой беззольной массы на рабочую массу. Такой расчет для тестовых условий (Наза-ровский бурый уголь марки Б2) дает 7,23 мас. %, что хорошо согласуется с данными, рассчитанным по методике ЭНИН. Подстановка значения μ^н_л = 7,23·ρ_г /(100·ρ_см) в формулу (10) дает возможность определить по описанной выше методике и по графику рис. 3: l н . = 0,21 м.

• 5.    Определение l н по экспериментальным данным для времени нагрева топливной пыли до воспламенения летучих веществ

• 6.    Определение lн по экспериментальным данным для Питтсбургского угля [8]

В работе [7] опубликованы результаты экспериментального исследования характеристик широкой гаммы энергетических твердых топлив в отношении воспламенения и выгорания частиц топливной пыли. В методическом и физикотехническом плане опыты тщательно проработаны и исполнены с применением специально изготовленной аппаратуры. В части определения длины начального участка факела приводится обобщенная зависимость времени воспламенения летучих веществ τ в.л в секундах как функция ряда факторов: температуры топочной среды Т г , К, размера частиц топлива δ, м, и опытного коэффициента пропорциональности k в.л , индивидуального для каждой марки угля [7]:

τ в.л = 5,3 ⋅ 10 ¹⁴ k в.л Т г ^{- 4} δ ^0,8 . (14)

При расчете по формуле (14) для тестовых значений Назаровского угля марки Б2 при k _в.л = 1,0 получаем τ_в.л = 0,04 с. При переходе к формуле (12) и учете аэромеханического коэффициента расширения факельной струи в виде k_F = (1 + 0,21 l _н / d ₀)^–2 получаем l _н = 0,25 м. Отклонение от аналогичных данных в п. 2 составляет +15…+18 %, что легко объясняется тем фактом, что в экспериментальных данных [7] приводятся данные, полученные при относительной скорости потока окислителя около 0,1 м/с, в то время как в реальном факеле, особенно в начальном участке, относительная скорость значительно выше. Поэтому согласование вышеприведенной методики с практическими данными [7] следует признать удовлетворительным.

В работе [8] приводятся данные экспериментального изучения показателей процесса горения угольной пыли из Питтсбургского битуминозного угля – по терминологии РФ из угля марки Ж. Опыты проводились на специальной установке, оборудованной устройством для отбора проб твердой и газообразной фаз. Содержание летучих веществ в исходном угле составляло 36 % на сухую массу, выводы акцентировались на частицы размером 200 мкм, несмотря на то, что основное число частиц располагалось в области 0–60 мкм.

Гетерогенный факел принимался одноразмерным, так как в нем отсутствовали рециркуляционные течения. Теплообмен факела с окружающей средой считался радиационным, конвекция и теплопроводность не учитывались. Проба газодисперсной факельной среды малого объема на анализ по содержанию летучих веществ отбиралась на определенном расстоянии от горелочного устройства, это расстояние пересчитывалось во время движения от горелки по известному распределению скорости потока.

Содержание летучих веществ в массовой доле от начальных 100 % определялось по содержанию влаги, золы и расчетному углероду; на временной абсциссе также фиксировалось расположение фронта воспламенения τ в.л = 0,051 с. Эти данные позволяют адаптировать результаты работы [8] к параметрам решаемой задачи.

В п. 5 была решена аналогичная задача для условий работы [7]; в эти данные необходимо внести изменения, связанные в марками углей: для марки Б2 было принято k _в.л = 1,0, для марки Ж необходимо ввести k _в.л = 0,85. Поэтому фактическое скорректированное время до воспламенения летучих веществ угля марки Ж составляет τ_в.л = = 0,051·0,85 = 0,04335 с и длина начального участка l н = 0,25 · 0,04335/0,04 = 0,27 м. Расхождение следует признать удовлетворительным с учетом всех погрешностей, связанных с экспериментами в работах [7, 8], а также того факта, что битуминозные угли по составу ближе к сапропелитам, а не к гумолитам, для которых построен рис. 1.

Выводы

Сформулирована математическая модель определения начального участка гетерогенного факела, позволяющая связать интегральную зависимость выгорания топлива с пространственными координатами факельного континуума Ф( u ) = F ( L ф ).

Разработанная математическая модель адаптирована к результатам теоретических и экспериментальных работ в этом направлении. Сравнение численных решений и экспериментальных данных с предложенной моделью показало достаточно удовлетворительное согласование, что подтверждает достоверность предложенной математической модели и надежность расчетов по ней для определения основных характеристик факела в зоне интенсивного горения котельных агрегатов.