Математическая модель подъёма воды в простых криволинейных капиллярах

Введение. Ксилема высших растений представляет собой сложную структуру. Вода в ней продвигается не прямолинейно. Это наглядно доказывает разнообразие форм растений. В работах [1, 2] предполагалось, что сосуды ксилемы прямолинейны, а движение воды может происходить как в вертикальном направлении восходящим током вдоль оси ствола, так и по горизонтали [2].

Многие растения имеют прямолинейные стволы. Однако боковые побеги и ветви часто выглядят как разнообразные математические кривые линии (рис. 1).

Рис. 1. Форма ветвей различных растений

В данном случае форма боковых побегов может быть объяснена сложным совместным воздействием на них ауксина и таких явлений, как отрицательный гравитропизм, фото-, термо- и хемотропизмы. Криволинейные ветви могут иметь самый разный вид. Так, например, ствол фанерофитов ([3], с. 133, рис. 68) вертикален, а форма боковых ветвей напоминает экспоненциальную кривую. Боковые побеги эвгалофита cолероса ( Salicornia sp. ) ([4], с. 242, рис. 231) внешне похожи на параболические кривые, попарно симметрично отходящие от прямолинейного ствола.

Точно так же расположены боковые побеги погремка большого ( Rhinanthus major ) ([4], с. 260, рис. 246). Лиана хмеля ( Humulus lupulus ), обвивающаяся вокруг опоры, образует цилиндрическую спираль ([4], с. 260, 261, рис. 247).

Габитус древесных растений также весьма разнообразен. И здесь можно найти побеговые системы, отходящие от стволов криволинейно [4] — в виде параболической кривой. То есть своею формой они напоминают конструктивные модели Аттимса, Лёйвенберга, Рау, Скарроне. Дихотомически ветвящиеся побеги куртинообразующего поликарлика можно сравнить с моделью Шута. В данном случае ветви первого порядка имеют экспоненциальную форму, ветви второго порядка — параболическую.

Для некоторых листьев характерно дуговидное жилкование, а черешок вместе с центральной жилкой листовой пластины может быть также криволинеен ([3], с. 250, рис. 153; [4], с. 31—36, рис. 29—36). Естественно, что ксилема таких растений (или отдельных их частей) должна быть криволинейной — т. е. соответствовать части растения, в которой она расположена. Криволинейность ксилемы предполагает пространственную кривизну составляющих её цепочек трахеид и сосудов.

Целью работы является уточнение модели движения воды в простых одноуровневых капиллярных системах с учётом их криволинейности.

Расчётная модель. Рассмотрим капилляр, расположенный наклонно к поверхности воды под углом β. Подъём h воды в наклонном капилляре [1] можно записать в виде:

2σcosα h= Lsinβ =         ,                                     (1)

rρg где α — угол смачивания, зависящий от молекулярного взаимодействия на границе раздела трёх сред: стенки капилляра, жидкости и воздуха; σ — коэффициент поверхностного натяжения; ρ — плотность воды; r — радиус капилляра; L — величина продвижения воды в надводной части капилляра.

Высота подъёма воды в наклонном капилляре над поверхностью воды согласно выражению (1) не зависит от угла наклона капилляра к поверхности воды.

Предположим, что капилляр радиуса r изогнут в виде кривой y = f(x) Введём декартову систему координат и совместим её начало с началом капилляра на поверхности воды при h = 0 (рис. 2, а ).

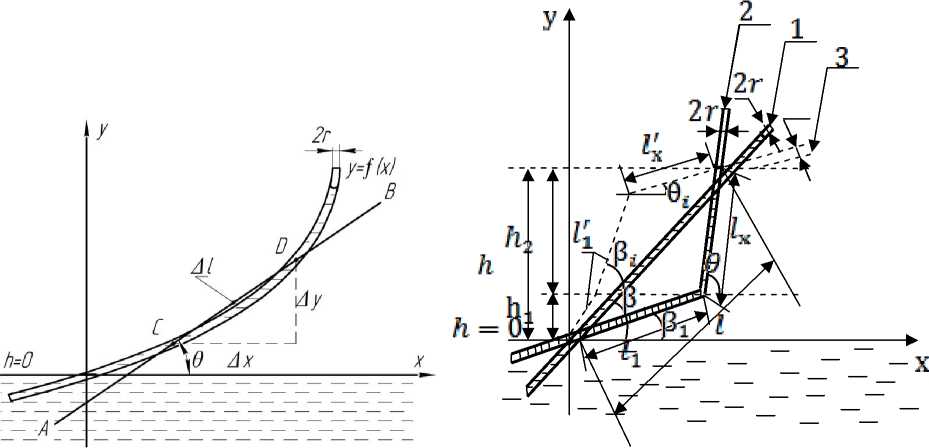
а )                                                              б )

Рис. 2. Криволинейный капилляр ( а ) и его расчётная модель ( б )

Условие равновесия воды в таком капилляре можно записать следующим образом

V ( x ) P ( x ) = 2nr ocosa,                                    (2)

где V(x) — объём поднимаемой в капилляре воды; P(x) — составляющая веса единицы объёма столба воды, противодействующая её подъёму.

Определим величины, входящие в левую часть уравнения (2). Для этого с помощью секущей АВ выделим на рассматриваемой кривой произвольный участок Δ l . Объём воды на этом участке может быть записан в виде

A V » n r ²А / .                                            (3)

Построим далее прямоугольный треугольник со сторонами Δ x и Δ y и гипотенузой CD. Тогда для A P ( x ) можно записать

A P ( x ) * р g sine,                                       (4)

где θ — угол наклона секущей АВ к горизонтали.

Если Δ l → 0, то Δ x → dx , Δ y → dy , а Δ l → dl . При этом секущая АВ превращается в касательную к рассматриваемой кривой в точке x , а тангенс угла наклона этой касательной tge = dy/dx или tge равен производной y' = f ' ( x ) .

Интегрируя (3) и (4) соответственно по l и по θ, уравнение (2) можно записать в виде nr 2p g J f (x )d/ J sine de = 2n ro cos a .

l 0

Вводя обозначение L ( x ) = J f ( x ) d/ и интегрируя по e, приводим уравнение к виду l

L ( x ) n r ²р g ( 1 - cose ) = 2n r ocosa.                               (5)

В уравнении (5) значения x и θ не определены. Из рис. 2, а видно, что θ также является функцией x . Для устранения неопределённости рассмотрим наклонный прямолинейный капилляр, исходящий из начала координат под углом β. Изогнём прямолинейный капилляр так, как показано на рис. 2, б . При этом нижняя часть капилляра длиной l 1 наклонена под углом β 1 , а верхняя часть расположена под некоторым углом θ.

Продвижение воды lх в таком капилляре может быть определено из соотношения nr2pg/1 sin в1 + nr2pg/x sine = 2nrocos a,(6)

откуда

/x sin e = hx = h - /1 sin₽1 = h - h1(7)

или h = h1 + hx.(8)

Аналогично можно показать, что при увеличении количества изгибов и любых изменениях угла βi (см. рис. 2, б, кривая 3) общая высота подъёма воды в капилляре всегда будет равна h. Изменится только величина продвижения воды, которая определяется наклоном конечного элемента кривой, то есть углом θi. Учитывая это, можно записать соотношение y = h = f (x).

Задавая функцию f(x), можно определить величину продвижения воды в криволинейном капилляре. Если капилляр описывается степенной функцией f (x) = h = kxn,                                          (9)

то x = n h / k , f ' ( x ) = knx n ^{- 1} = kn ( ^ h / k ) n 1 = tg e.

Тогда

0 = arctg

kn ( ^ h / k ) n

и уравнение (5) примет вид

π r

2 P gL ( x ) 1 1 - cos arctg kn ( n h / k )

n - 1

= 2nrо cos a .

Отсюда, полагая, например, k = 1, n = 2, получим

L ( x ) =

h

1 - cos arctg 2V h

При k * 1 кривая по сравнению с f(x) = x вытянута в направлении оси OY в | k | раз.

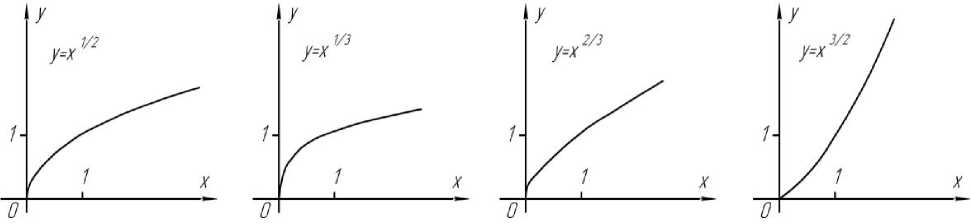
Рис. 3. Степенные функции, соответствующие криволинейным капиллярам различной формы

Аналогично можно показать (рис. 3, 4), что при у = h = x ²

L ( x ) =------ h Г,

1 - cos arctg 2 h

при у = h = x ³

L ( x ) =------ h ----_Г,

1 - cos arctg— 3 h ²

при у = h = x ³

^{L ( x} ) =------- h ----2-,

1 - cos arctg— 3 h

при у = x ³

^{L ( x} ) =

h

1 - cos arctg 3 3 h

При у = a^x - 1

^L ( ^x ) =

h

r ln ( h + ¹ )       ^ .

1 - cos arctg a a In a

L(x ) =

h

1 - cos arctg ke ^{ln( h +1)}

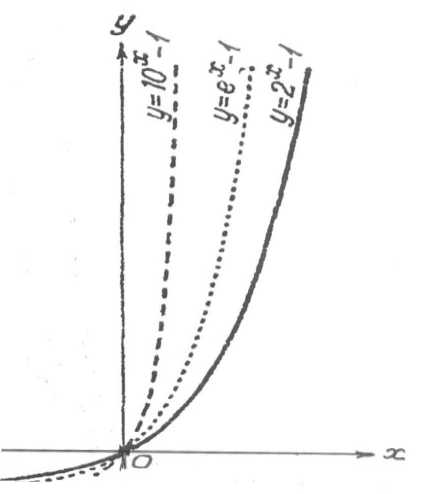
Рис. 4. Виды показательных функций, соответствующих криволинейным капиллярам различной формы

В уравнениях задания кривой для (17), (18) введено слагаемое (–1), чтобы кривая при х = 0 проходила через начало координат.

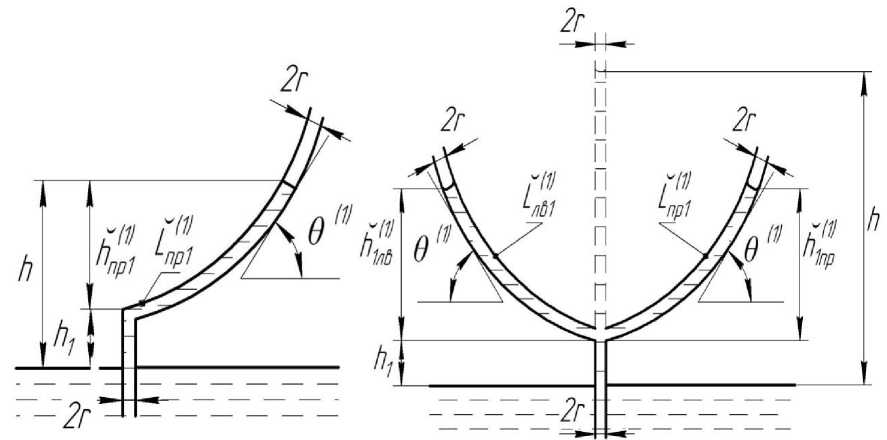
а )                                                        б )

Рис. 5. Криволинейные одноуровневые капилляры: несимметричный ( а ), симметричный ( б )

Рассмотрим подъём воды в капиллярной системе при условии, что к вертикальному капилляру присоединяются боковые криволинейные капилляры одинакового радиуса r . Примем следующие обозначения индексов для величин L , h и θ:

• —    верхний индекс в скобках указывает общее количество уровней боковых ветвей в рассматриваемой модели;

• —    нижний индекс указывает номер уровня, к которому относится рассматриваемая величина;

• —    дуга над L , h показывает, что рассматриваемая величина относится к капиллярной системе с криволинейными элементами.

Пусть капилляр имеет форму, изображённую на рис. 5, а. То есть имеет вертикальную часть (высотой h1) и обращённую вправо криволинейную, описываемую степенной функцией y (x) = h1 + kxn.                                           (19)

Уравнение подъёма воды в таком капилляре может быть записано в виде nr 2p gh + nr 2рд2Прр) (x) = 2nr ocosa, откуда

L- ll^p ) ( x )( 1 - ^cos0 ) = ^{h -} h i .

В полученном уравнении необходимо определить величину продвижения воды в криволинейной части капилляра. Учитывая, что согласно (8) высота подъёма воды в капилляре не может превосходить h, запишем (19) в виде h - h1 = kxn.

Отсюда x = n

h - h 1 k

и тангенс угла наклона касательной к конечному элементу, то есть к мениску воды в капилляре, согласно (10) примет вид f'(x) = knxn-1

= kn

h - h 1

N k

к

X n -1

= tge,

0 11 ) = arctg

л

kn

к

h - h 1 k

n n - 1

Согласно (20) с учётом (22)

L n ) ( x ) =

h - h 1

г               г

1 - cos arctg kn

к

n ^{h - h} 1

tv   k

n - 1 ПП

J 7

Очевидно, что при h 1 = 0 уравнение (23) совпадает с (12), а при h 1 = h вода не продвигается в криволинейную часть капилляра. Но в целом продвижение воды в таком капилляре, в отличие от прямолинейного, зависит от величин k и n в уравнениях (22) и (23). Из (22) можно видеть, что изменение обеих этих величин приводит к изменению угла наклона к горизонтали касательной в точке нахождения водяного мениска в капилляре. В рассматриваемом случае нас интересует главное значение функции арктангенса в интервале от 0 до +π/2. Если арктангенс равен нулю, что соответствует углу наклона θ → 0°, то второе слагаемое в знаменателе (23) стремится к единице, а величина продвижения воды в капилляре 2^^_р ) ^ да , как и в прямолинейном капилляре. Такой случай реализуется при k → 0. Если арктангенс принимает значение +π/2, что соответствует углу наклона θ → 90°, то второе слагаемое в знаменателе (23) стремится к нулю, а L^nр ) ^ ^{h - h} 1 .

Высота подъёма воды в криволинейной части капилляра определяется из соотношения

L i n ) ( ^x ) = ^{1 -} cosarctg

kn

I h - h 1 к

n - 1

= h - h = h -⁽¹⁾. .

¹         1 ( пр )

Следует заметить, что величина продвижения воды в криволинейном капилляре всегда больше, чем в наклонном прямолинейном с углом наклона, равным углу наклона касательной к мениску в криволинейном капилляре. Действительно, продвижение воды в прямолинейном наклонном капилляре определяется соотношением [1]:

L^ X = h - h l

.

^{4( пр )(} ) sine

Если согласно (22) в = 0 11 ) , то

1 - cosarctg kn

^LпP ) L р ) =

sinarctg kn

⁽ h — h n

П k

n - 1

V h — h

v к

V 7

n - 1

При arctg → 0 числитель и знаменатель стремятся к 0, образуя неопределённость вида 0/0. Физический смысл её в том, что и наклонный прямолинейный, и криволинейный капилляры становятся параллельными оси абсцисс и продвижение воды в них стремится к ∞. При arctg 90° отношение L пр) jL^nр) = 1, оба капилляра совпадают с осью ординат и вода в них поднимается как в обычном вертикальном капилляре. При изменении угла от 0 до 90° ^1пр)^пр) < 1, так как при этом числи тель в последнем соотношении для L1np)/^р) всегда меньше знаменателя. Это означает, что в криволинейных капиллярах при прочих равных условиях содержится больший объём воды, чем в прямолинейных.

Представим капиллярную систему — как показано на рис. 5, б . Примем радиусы в обеих криволинейных ветвях равными r . В этом случае на вертикальную часть воды высотой h 1 одновременно и в равной степени будут действовать силы поверхностного натяжения обеих криволинейных капиллярных ветвей. Тогда сила, необходимая для подъёма воды на высоту h 1 , распределится поровну в обеих ветвях, и каждая криволинейная ветвь будет поднимать половину объёма воды в вертикальной части. Как и для правой ветви, введём обозначения для продвижения и подъёма воды для левой ветви соответственно L ^^ _в ) и h ^) .

Уравнение равновесия воды в рассматриваемой системе можно записать для правой и левой ветвей соответственно в виде:

2nr 2р gh + nr 2р g^р) (x) = 2nr ocosa,(25)

2 nr 2pgh + nr 2pgL\в) (x) = 2nr o cosa.(26)

Учитывая, что половина объёма воды вертикальной части пропорциональна половине высоты h1, уравнение (19) можно записать в виде h — h +1 h = h —1 h = kxn.

1    21

Отсюда nh — 0,5h1 x = n k '

0 11 ) = arctg

kn n

----------------x n —1

h — 0,5 h 1 ]

V

k

.

Физический смысл (27) заключается в том, что мениски воды в обеих ветвях поднимаются выше — и в соответствии с этим увеличивается угол наклона к горизонтали касательной к мениску. Это соответствует величине вертикальной части капилляра над поверхностью воды и равной 0,5 h ₁ .

Уравнения (25) и (26) можно записать относительно /Пр) (x) и /лв) (x) в виде спр>(*)(1 -cos^' h-o,5hi=h?,,

/ Л. ) ( x )( 1 - cos0 ) = h - 0,5 h i = /- 1 ,1)

После простых преобразований получим

/ XI)   = №)

4 ( пр )   Ч( лв )

h - 0,5 / 1

1 - cosarctg

V

, ( Ih - 0,5 / ) kn n ---—¹

V

n -1 1^

k

J 7

Из (27), (30) видно, что величина под радикалом при прочих равных условиях больше аналогичной в (22) и (23), то есть увеличивается угол θ(1). Одновременно увеличиваются продвижение и высота подъёма воды в криволинейных капиллярах.

Определяя из (30) высоту подъёма воды и вычитая из неё высоту, полученную в (24), можно видеть, что высота подъёма воды при наличии двух ветвей увеличивается

( h - 0,5 h 1 ) - ( h - h 1 ) = 0,5 h 1 . (31)

Усложним предыдущую капиллярную систему, добавив к ней центральный вертикальный капилляр (см. рис. 5, б ). Предположим, как и прежде, что радиусы всех ветвей одинаковы и равны r . Обозначим общую высоту подъёма воды в вертикальном капилляре как h = h ^ . В этом случае объём воды в нижней части системы высотой h 1 находится под действием трёх одинаковых сил. Угол θ и уравнения продвижения воды в криволинейных и вертикальном капиллярах могут быть записаны следующим образом:

0 11 ) = arctg

₃ π r ²ρ gh ₁

₃ π r ²ρ gh ₁

^{п г 2}р g ( /’2 б

kn

( I I h -1 h n__3—

V k

x n -1

+ п г ²р д/ ₁ ⁽ ₍ ¹ П_р ) ( x ) = 2n r о cos а, + п r ²р д/ 1 лв ) ( x ) = 2п г о cos а,

—

h 1 ) + 3 п г ²р gh 1 = 2n r о cos а .

Решениями этих уравнений относительно / П_р ) ( x ) , / Лв ) ( x ) и h^ будут

/ t¹)  =_

( пр )     (

h — h

1 -

cosarctg kn ^

1        )'

h -T h k

П -11^ ,

V

^J 7

h ’i⁽¹>6 = h - ¹ h + h = h + 2 h .

1 об 3 1      1           3 1

Выводы. Анализ полученных соотношений для одноуровневой капиллярной системы позволяет сделать следующие выводы.

— При увеличении количества ветвей продвижение воды в криволинейных ветвях одноуровневой капиллярной системы увеличивается (по сравнению с одиночным криволинейным капилляром) и является функцией угла наклона к горизонтали касательной к водному мениску.

— Общая высота подъёма воды в прямолинейном вертикальном капилляре также увеличивается по сравнению с одиночным вертикальным капилляром такого же радиуса и не зависит от вида функции, описывающей кривизну присоединённых боковых криволинейных капилляров.

— Уравнение (37), описывающее подъём воды в вертикальном капилляре рассмотренной системы, совпадает с (19), полученным в [1].

— При прочих равных условиях объём воды, поднимающейся в боковых криволинейных ветвях капилляров, больше, чем в прямолинейных.