Математическая модель полностью оптической системы детектирования параметров распространения мод в оптическом волокне при маломодовом режиме для адаптивной компенсации смешения мод

Современный уровень использования оптического волокна (ОВ) ограничен в традиционных областях (временной и частотной) и стремится к пределу пропускной способности, обусловленному нелинейными эффектами [1]. Однако объём мирового трафика ежегодно возрастает примерно в полтора раза из-за увеличивающихся потоков данных HD-видео, распределённых вычислений и других приложений [2]. Для обеспечения соответствия сетей связи постоянно растущим требованиям по пропускной способности необходимо рассмотреть дополнительные подходы к уплотнению каналов в ОВ. В связи с этим в последние годы чрезвычайно возрос интерес к телекоммуникационным системам с пространственным разделением каналов (spatial division multiplexing – SDM).

Технология SDM в оптическом волокне может быть реализована с помощью волокон с несколькими сердцевинами [3] или с помощью модового мультиплексирования (mode division multiplexing – MDM) в ОВ при маломодовом режиме передачи [4]. Волокна с несколькими сердцевинами предполагают сложное изготовление по сравнению с волокнами с осевой симметрией, поэтому системы MDM представляются экономически более эффективными. Однако при реализации телекоммуникационных систем на основе MDM возникают две основные проблемы:

• а)    возбуждение определённой суперпозиции мод с заданным распределением э нергии и фазы в передатчике и выделение отдельных мод в приёмнике.

• б)    преодоление эффекта смешения мод.

Разработано множество методов возбуждения мод низшего порядка. Моды произвольных порядков могут быть эффективно выделены из лазерного пучка посредством оптического корреляционного анализа. Данный подход использует дифракционные оптические элементы (ДОЭ), согласованные с определён- ными модами и называемые МО ДАНами [5 –9], которые позволяют генерировать и выделять люб ую комбинацию мод с точно заданными комплексными весовыми коэффициентами. ДОЭ позволяют достичь пика интенсивности желаемой моды в центре соответствующего дифракционного порядка при интенсивности в других порядках, близкой к шуму (не более 10% от пиковой интенсивности) [6, 7].

Как известно, явление смешения мод зависит от времени и обусловлено дефектами ОВ, такими как флуктуации диаметра волокна и профиля показателя преломления, а также микроизгибы [4, 10, 11]. В результате отдельные моды обмениваются энергией, распространяясь по ОВ. Кроме того, дифференциальная модовая задержка (differential mode delay – DMD) и хроматическая дисперсия (chromatic dispersion – CD) приводят к межсимвольной интерференции (МСИ) в каналах, передаваемых отдельными модами.

В целях предотвращения смешения мод в настоящее время разрабатываются два основных подхода:

• а)    мультиплексирование по орбитальному угловому моменту (OAM), основанное на создании в ОВ ортогональных, пространств енно разнесённых потоков [12];

• б)    модовое мультиплексирование по технологии «множественный вход, множественный выход» (multiple-input multiple-output – MIMO), основанной на электронной коррекции межмодовой интерференции [12, 13].

Оба эти подхода обладают своими достоинствами и недостатками.

Мультиплексирование по OAM осуществляется полностью оптическим способом и не требует каких-либо вычислительных ресурсов, однако предполагает использование специального волокна со сложным профилем показателя преломления для достижения достаточной дальности передачи без существенного взаимного влияния между модами.

В системах с MIMO MDM, наоборот, проблема смешения мод решается только средствами цифровой обработки сигнала (ЦОС). Данный подход позволяет использовать потенциально любое волокно, в котором обеспечен маломодовый режим (маломодовость понимается в общепринятом смысле [7]), в том числе существующие волокна со ступенчатым профилем показателя преломления, возбуждаемые светом с длиной волны ниже длины волны отсечки [7, 15, 16]. Примечательно, что дальность передачи для MIMO MDM с использованием маломодового ОВ с низкой дифференциальной групповой задержкой (differential group delay – DGD) может достигать более чем тысячи километров [17]. Однако данный подход требует сложных алгоритмов обработки MIMO-сигнала, поэтому он потенциально ограничивает скорость модуляции в канале и может приводить к росту потребляемой мощности.

След ует заметить, что два указанных подхода разрабатываются независимо, хотя совместное их рассмотрение могло бы привести к синергетическому результату по направлению к компенсации смешения мод в оптической области.

Модель MIMO MDM-канала

Рассмотрим MIMO-систему N × N . В общем случае, когда присутствуют DGD (об условленная в основном эффектами DMD и CD) и смешение мод, наблюдаемая последовательность y ν [ k ] на ν -м выходе может быть выражена как свёртка

У _l ^{[ k ]} =

NL

= ЕЁ h J l b x J k - 1 ] + n I k ], (1 ⁵ v^ N ),

M = 1 1 = 0

где x µ [ k ] – входная сигнальная последовательность, h µν [ k ] – импульсная характеристика со входа µ на выход ν , n ν [ k ] – шумовая последовательность на ν -м выходе. Здесь L означает максимальную память канала среди всех модовых каналов, выраженную в количестве символов. Это равенство может быть также определено в матричной форме:

• y [ k ] = ^L H [ l ] ⋅ x [ k - l ] + n [ k ]. (2) l = 0

Если DGD некоторым образом преодолена, то сложность обработки MIMO-сигнала существенно снижается. В частности, DGD может быть скомпенсирована при использовании ортогонального частотного мультиплексирования (orthogonal frequency domain multiplexing – OFDM) поверх каждого модового канала [13, 18]. Тогда выражение (2) упрощается:

У V = E N = 1 h ,V x M ⁺ n V , ^{(1 5v5} N ). ⁽³⁾

Разработано множество методов пространственной коррекции MIMO-канала, включая как линейные (такие как сведение к нулю и коррекция по критерию минимума СКО на приёмной и передающей стороне), так и нелинейные методы (такие как матричная коррекция с реш ающей обратной связью и MIMO- предкодирование) [17]. В простейшем случае коррекции по критерию сведения к нулю (zero-forcing – ZF) оценка переданной последовательности может быть получена путём восстановления из равенства

• X ^ˆ = H ^{- 1} Y .                                       (4)

Согласно матричной модели распространения [9], MDM-канал может быть представлен оператором распространения M ( o^ = TT f M, (to) , где каждая k -я k = 1

матрица размером N × N описывает распространение сигнала через k -й участок ОВ или входящий в линию элемент:

M k (0= V _t Л k (O U } ,                       (5)

где Λ k (ω) – диагональная матрица, описывающая распространение мод без смешения и включающая DMD, CD и модово-зависимые потери (MDL); V k и U k – частотно-независимые унитарные матрицы, описывающие смешение мод на входе и выходе k -го участка соответственно, при этом каждый участок должен быть незначительно больше длины корреляции волокна. Так как в обычных многомодовых системах используются светодиоды, некогерентные в пространстве и во времени, классическая модель смешения мод принимает во внимание обмен энергией между модами и определяется вещественными коэффициентами [18]. Однако, учитывая, что MDM-системы предполагают когерентное лазерное излучение, необходимо использовать комплексные матрицы V k и U k [11].

Физическая модель MDM-канала

Рассмотрим процесс маломодового распространения света в традиционном ступенчатом волокне с радиусом a , показателем преломления сердцевины n 1 и показателем преломления оболочки n 2 . Большинство коммерческих волокон относятся к слабо-направляющим волокнам, в которых разность межд у показателями преломления Δ n = n 1 – n 2 составляет менее 1% [15]. В этом случае уравнение на собственные значения [19] приводит к собственным решениям для мод, которые являются практически линейно поляризованными (моды LP). Тогда их доминирующая компонента электромагнитного поля выражается как:

Ψpq(u,z)= Ψpq(u) exp(-iβpqz) = exp(-iβpqz) exp(ipϕ)

' J p ⁽ Upq r / a ) _t      J p (U pq ) ,

^Kp - 1 ⁽ w pq r / a ) ,    K p ( W pq )

0 ≤ r ≤ a ,

, a ≤ r ≤ b ,

где u = ( r , ϕ), пар аметры u p q и w pq вы ражаются как u = a ( k ₀ n ₁)² -β² и w = a β² -( k ₀ n ₂)² , β – коэффициент распространения, k ₀ = 2π/λ₀ , а целые числа p и q обозначают азимутальный и радиальный индексы мод соответственно.

На рис. 1 прив едены распределения амплитуды в поперечном сечении для некоторых LP-мод. Возбу- дить такие моды в оптическом волокне можно с помощью спиральных фазовых пластинок или многоуровневых ДОЭ [20].

Так как собственные решения Ψ pq ( u ) образуют базис ортогональных функций, так что

Ψpq,Ψ   =  Ψ* (u)Ψ (u)d2u = pq mn          pq mn

ℝ2

= δ ( p - m , q - n ) ,

любая линейная суперпозиция LP-мод, определяемых выражением (6), в постоянной точке z может быть представлена в виде ряда:

Ψ ( u )= ∑ ψ [ p , q ] Ψ _pq ( u ), p , q

где ψ [ p , q ] – комплексные коэффициенты, определяющие распределение мод и выражаемые как [9]:

С точки зрения квантового подхода каждый фотон переносит OAM, выражаемый как pħ [21], так что каждая LP-мода переносит OAM, пропорциональный индексу p . Если мы рассмотрим только набор из N = (2Λ + 1) мод, различающихся индексами p (индекс q будем считать постоянным, а коэффициенты ψ [ q ] равными единице), тогда линейная суперпозиция LP-мод, подаваемых на вход в волокно, может быть записана как:

Ψ ( u , z )= ∑ ^Λ _{p =-Λ} ψ [ p ] Ψ _pq ( r , z )exp( ip ϕ ) .          (10)

В [22] экспериментально доказано, что распределение углового момента ψ [ p ] и угловое распределение Ψ ( ϕ ) монохроматического светового поля связаны преобразованием Фурье, т.е.

1 π

ψ [ p ]=       Ψ ( ϕ )exp( - ip ϕ )d ϕ .               (11)

2π - π

Выражение (13) связано с (9), но описывает частный случай , когда используются только моды, переносящие OAM. В квантовом режиме, как известно, это соотношение через преобразование Ф урье связано с принципом неопределённости Гейзенберга.

Принципы оптической компенсации смешения мод

Если пучок с поперечным распределением поля Ψin(u) падает на амплитудно-фазовую голограмму с функцией передачи ΨH(u), то распределение мод в выходном пучке согласно (9) может быть выражено как:

ψ out [ p , q ]= ∫∫ Ψ in ( u ) ⋅Ψ H ( u ) Ψ ^* pq ( u ) d ² u . (12) ℝ ²

Таким образом, было бы целесообразно предположить, что можно скомпенсировать смешение мод с помощью некоторой реконфигурируемой амплитудно-фазовой голограммы Ψ H ( u ), приближённо инвертирующей частотно-независимую часть оператора распространения ОВ M ( ω ).

Рассмотрим линейную MDM-систему N × N , описываемую матрицей распространения M ( ω ) = W Λ ( ω ), результирующей влияние всех K уч астков волокна, где частотно-независимая матрица W = ∏ _k ^K = 1 V k U k описывает общее смешение мод.

Как известно, в реальном волокне, являющемся распределённой системой, каждая мода претерпевает смешение с другими модами своим уникальным образом [9], поэтому оператор W и приближённый обратный оператор W ^–1 в общем случае не могут быть смоделированы одной голограммой с амплитуднофазовым распределением Ψ mask ( u ) (иначе должно было бы выполняться соотношение ∀µ , ν : w µν = w ( µ +1)( ν +1) ,).

Оператор W ^–1 становится физически реализуемым при использовании МОДАНа, формирующего одномодовые пучки в различных дифракционных порядках [6– 9]. Данный подход позволяет пространственно разделить моды в дальней зоне и обрабатывать их независимо. В этом случае ДОЭ, формирующий одномодовые пучки в дифракционных порядках, в соответствии с их коэффициентами ψ [ p , q ] имеет функцию передачи:

ΨDOE(u)=∑Ψ*pq(u) exp(ivpqu) , (13) p,q где vpq – пространственные несущие частоты в дальней зоне, реализуемой путём применения линзы с соответствующим фокусным расстоянием.

В общем случае такой реконфигурируемый ДОЭ является амплитудно-фазовым, но может быть закодирован как фазовая голограмма [6, 8, 15, 20, 23 –25] и затем реализован с помощью пространственного модулятора света (spatial light modulator – SLM).

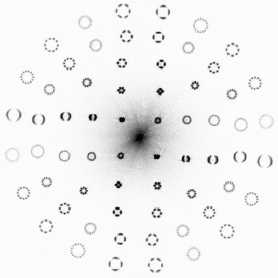
На рис. 2 показано формирование 64 дифракционных порядков с отдельными LP-модами и их суперпозициями с помощью бинарного фазового ДОЭ.

Другая проблема возникает в связи с тем, что смешение мод в отдельном ОВ зависит от времени и определяется такими факторами, как температура кабеля и механическая деформация. Поэтому компенсирующий ДОЭ должен быть адаптивным со временем адаптации не более времени корреляции смешения мод MDM-канала. Это условие легко реализуемо на практике, поскольку указанные выше факторы являются достаточно инерционными по сравнению со временем переключения в электронных компонентах системы. Для оценки MDM-канала рассматривается общепринятый подход с применением тестирующего сигнала. Важным является соблюдение условия T tr >  τ GD , где T tr

– длительность каждого тестового символа, τ GD – мак-

симальная память модового канала.

Это условие обязательно для отделения матрицы

W от частотно-зависимой матрицы Λ ( ω ). Таким обра-

зом, пропуская последовательно тестирующие сим-

волы g µ через каждый µ -й модовый канал, мы можем определить кажд ую строку матрицы W , состоящую

из элементов w µν , ν = 1… N .

б)

(3,4).

(10,1)      *

,^--^к

X’ (i.3)/ < ,* " (1,4)

Рп ' >

o^X^ (&2)

(2.3) a. '

’'^'.^У)

(2,2) X (4.2)

^x' X '(6,2) (2.1)0(44) . ^ a < ’ <1(6,b)

\(0.3) (0,5) '6

‘(0,2)1 ((l,4)°(U!D

Рис. 2. Бинарная фаза кодированного 64-порядкового ДОЭ (а), экспериментально зафиксированное распределение

интенсивности в фокальной плоскости линзы при освещении ДОЭ плоской волной (б), схема расположения LP-мод

с номерами p = 0,11 , q = 1,5 (сопряжённые моды с p = -11, 0 располагаются симметрично в нижней части)

Как было указано выше, матрица W является комплексной, поэтому должны быть точно определены не только амплитуды её элементов | w µν |, но и межмодовые фазы φ µν . Для получения всей информации о коэффициентах w µν может быть использован известный подход, основанный на сенсоре Шака–Хартманна [26, 27]. Принятая информация о форме фронта позволяет декомпозировать моды, используя выражение (9). Но для целей построения MDM-систем более предпочтительной представляется реализация всей обработки пучка только посредством ДОЭ. Во-первых, использование ДОЭ позволяет непосредственно извлечь распределение мод с минимальной вычислительной сложностью. Во-вторых, технология производства голограмм, генерируемых с помощью компьютера, достаточно развита для получения высокой разрешающей способности и точности, а также обладает потенциалом экономической эффективности при последующей интеграции в промышленные приложения.

Эффективный метод полной декомпозиции мод в режиме реального времени, использующий интерферометрическую суперпозицию между опорной модой и тестируемой модой, описан в [6, 9, 23, 24]. Соответствующий МОДАН имеет два дополнительных дифракционных порядка на каждую моду. Таким образом, анализирующий ДОЭ описывается функцией передачи:

v DOT ( u )= E ^ ( u )exp( i v pq u ) + p , q

+ 4 ^ ( ^V P 0 q o ( u )+ ^V Pq ( u ) ) exp( i v P 7u) + (14) 2 [ p , q ] ≠ [ p ₀ , q ₀ ]

⁺ E ( ^ P 0 q 0 ^{( U )+} i ^ Pq ^{( U )} ) exP⁽ i ^V P n ^{U )}, 2 [ p , q ] ≠ [ p ₀ , q ₀ ]

где Ψ _{p 0 q 0} ( u ) обозначает распределение поля моды, фаза которой φ [ p 0 , q 0 ] выбрана в качестве опорной. В этом случае селективный ДОЭ должен обладать (3 N –2) порядками для получения комплексных коэффициентов w µν [6, 9, 23, 24]. Этот анализирующий ДОЭ может быть закодирован как амплитудная или фазовая голо-

грамма и реализован с помощью лазерной литографии. В итоге, коэффициенты матрицы смешения мод W определяются как:

И’ = μν

× exp

w _μν exp( i φ _μν ) =

(

- i I arctan

I V

2 I ν^sin

ψ [ ν ] g _μ

-

cos ν

exp( i φ _μν )=

f I ν 2 π k ₀ g _μ

×

I _ν - I ₀

-

I _ν - I ₀

))

- ^arg⁽ g _M ) I

vy

µ,ν =1...N, где gµ – тестирующий символ, соответствующий µ-й передаваемой моде; Iν – интенсивность света в дальней зоне анализирующего ДОЭ, соответствующая ν-й принимаемой моде и задаваемая пространственной несущей частотой vpq. Предполагается, что каждая передаваемая µ-ая мода и принимаемая ν-ая мода определяются своим собственным набором индексов [p, q], когда µ = ν. Значения Iνsin и Iνcos описывают интенсивности в дальней зоне в соответствии с пространственными несущими частотами vspinq и vcpoqs соответственно; I0 – интенсивность в дифракционном порядке, соответствующем модовому коэффициенту, фаза которого рассматривается в качестве начальной (например, w11). В выражении (15) f – фокусное расстояние линзы.

В описанном случае в целях упрощения мы считали, что все моды линейно поляризованы. Однако общий случай оценки MDM-канала с произвольно поляризованными модовыми каналами может быть обеспечен с помощью метода, представленного в [23, 24].

Как и в случае любой технологии коррекции, приближённая реализация обратного оператора распространения может быть осуществлена как на передающей, так и на приёмной стороне. Концепция предварительной компенсации, как известно, позволяет избежать усиления помехи, которое может возникать при применении приближённого обратного оператора распространения к принимаемому сигналу с аддитивным шумом. Однако данный подход требует информации о состоя-

нии канала на передающей стороне. В настоящее время для определённости будем считать, что компенсация смешения мод осуществляется на приёмной стороне, однако сравнение данных двух концепций является предметом последующих исследований.

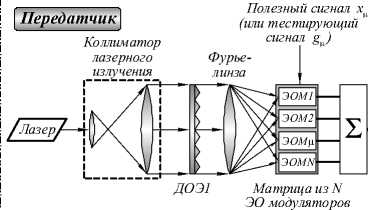
Модель MDM-системы с оптической компенсаци- ей смешения мод показана на рис. 3, где постоянный ДОЭ1, имеющий N дифракционных порядков и фор- мирующий одномодовые пучки в различных дифракционных порядках, предназначен для возбуждения мод; постоянный интерферометрический ДОЭ2, имеющий (3N –2) дифракционных порядков, предназначен для декомпозиции мод в процессе оценки MDM-канала; основанный на SLM программируемый

ДОЭ3 применяется для приёма полезного сигнала с адаптивной компенсацией смешения мод.

Оптическое волокно

W

Фурье-линза

Матрица из N ЛФД

Вычисление W ^–1 и ко дирование SLM

Принимаемый сигн ал ˆxν   ( Приемникji

Делитель пучка

Волоконнооптический коллиматор

ДОЭ3 на осн ове SLM

Фурье-линза

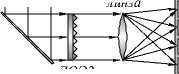
ДОЭ2

ЛФД2

ЛФД ν ЛФДN]

Матрица из (3N–2) ЛФД

Рис. 3. Модель N × N MDM-системы с оптической компенсацией смешения мод (ЭОМ – электрооптический модулятор, ЛФД – лавинный фотодиод, SLM – пространственный модулятор света)

Согласно (4) и (13), компенсирующий ДОЭ3 б удет описываться функцией передачи:

ΨNN cDoOmEp(u)=∑ ν=1(∑i=1wμ-ν1Ψ*μ(u))exp(ivνu) , (16) где wµν – коэффициенты матрицы W–1, обратной к матрице смешения мод W; Ψµ(u) – распределение поля моды, соответствующей µ-му каналу на передающей стороне; vν – пространственная несущая частота, соответствующая ν-му каналу на приёмной стороне. Тогда для программирования SLM компенсирующий ДОЭ3, определяемый выражением (16), может быть закодирован как фазовый отражающий ДОЭ при использовании известных методов, описанных в [6].

Матрица Λ ( ω ), описывающая частотно-зависимые искажения, может быть компенсирована путём коррекции во временной или частотной областях, но порядок корректора будет в ( N ) раз меньше, чем для классической MIMO-системы. Однако более эффективным представляется одновременное применени е оптической компенсации смешения мод и OFDM.

Выводы

В данной работе предлагается метод, предназначенный для компенсации искажений, вызванных смешением мод в системах передачи с MDM, основанный на обработке сигнала полностью в оптической области. Предлагаемый метод основан на пространственно-спектральной взаимосвязи между модовым составом и распределением электромагнитного поля в лазерном пучке и на использовании дифракционного оптического элемента, программируемого в режиме реального времени. Несмотря на то, что этот метод направлен только на компенсацию эффекта смешения мод, он рассматривается как способ значительного снижения вычислительной сложности будущих коммерческих MDM-систем. Благодаря компенсации смешения мод в оптической области может быть исключена сложная цифровая обработка сигнала и тем самым повышена скорость передачи данных.