Математическая модель преобразователя частоты с автономным инвертором напряжения

Цитирование: Федоренко, А. А. Математическая модель преобразователя частоты с автономным инвертором напряжения / А. А. Федоренко, А. Н. Пахомов // Журн. Сиб. федер. ун-та. Техника и технологии, 2022, 15(1). С. 90–100. DOI: 10.17516/1999-494X-0376

римента. Таким образом, существует задача создания достаточно универсальных, наиболее полно учитывающих особенности и позволяющих проводить широкий спектр исследований математических моделей таких систем. В настоящей работе предложен вариант такой модели и представлены некоторые результаты выполненных с её помощью исследований.

Применение виртуальных моделей [1, 2], получивших распространение в практике моделирования, удобно для анализа процессов в системе электропривода в целом, однако они не позволяют проследить физическую природу протекаемых в них процессов и увидеть функциональные связи между переменными каждого отдельного элемента ПЧ в процессе их взаимодействия. Более универсальным представляется подход, принятый в настоящей работе, – построение модели ПЧ с формализацией в виде математических соотношений взаимосвязей между переменными, характеризующими его функционирование, на основе анализа физических процессов в каждом его элементе. Далее математические модели каждого элемента представляются структурными схемами, которые объединяют в общую структурную схему ПЧ согласно его схеме в соответствии с методом структурного моделирования. Такой подход позволяет создать достаточно универсальный и гибкий вариант полной математической модели объекта исследования, поскольку здесь имеется возможность достаточно просто включать в нее различные варианты математических моделей элементов, входящих в конкретный реальный ПЧ.

Разработанная на основе такого подхода структурная схема ПЧ с автономным инвертором напряжения (АИН) с ШИМ показана на рис. 1. Эта схема включает в себя структурные схемы трехфазного входного трансформатора, трехфазного мостового диодного выпрямителя, силового LC -фильтра звена постоянного тока, АИН с ШИМ и нагрузки АИН в виде трехфазной RL -цепи.

В основу построения математической модели трансформатора положена Т -образная схема замещения его фазы, учитывающая потери на перемагничивание его сердечника [3].

Уравнения баланса напряжений для этой схемы замещения при построении структурной схемы трансформатора удобно привести к следующему виду:

"T = (M1-(^1 + Rm)h +Lm~77 + RmhV {Lx +Lm), (1) at at u2=V^^Lm\—^\Rld-Rm\i2-RTniY-Lm—, (2) v ' dt ’ dt где u 1, i 1, u2, io — мгновенные значения фазных напряжений и токов первичной и вторичной обмоток трансформатора соответственно; R 1, L1, Ro, Lo - активные сопротивления и индуктивности рассеяния первичной и вторичной обмоток трансформатора соответственно; Lm, Rm - индуктивность намагничивания и фиктивное сопротивление, учитывающее потери на гистерезис и на перемагничивание сердечника.

Все переменные и параметры приведены к вторичной обмотке трансформатора.

Уравнения (1) и (2) легко позволяют составить структурную схему для одной фазы трансформатора. Полная модель трансформатора представляет собой комплект из трех таких схем (см. рис. 1). Особенностью структурной схемы является то, что здесь физически не реализуемая операция чистого дифференцирования тока вторичной обмотки трансформатора заменена

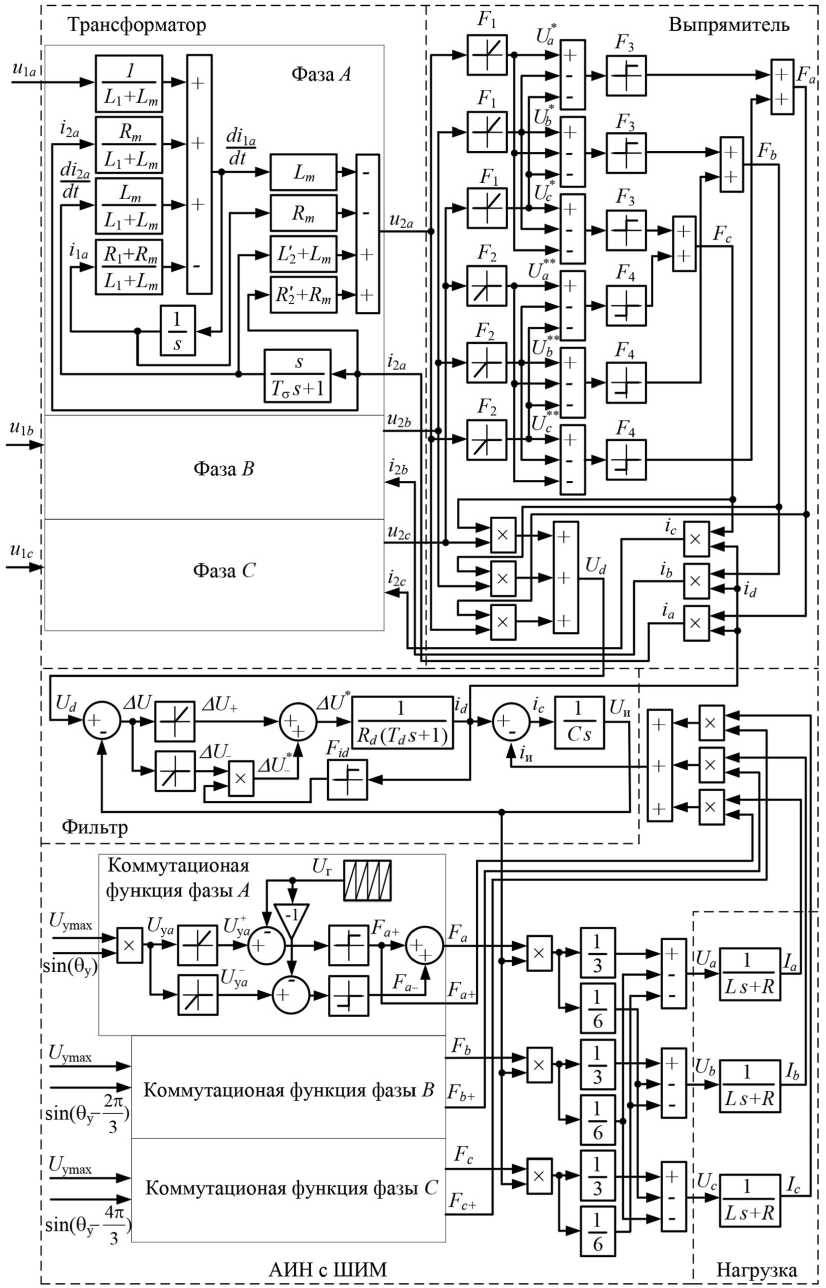
Рис. 1. Структурная схема преобразователя частоты операцией дифференцирования со сглаживанием. Такая замена физически обоснована тем, что ток из одной фазы трансформатора в другую при коммутации вентилей выпрямителя переходит не мгновенно, а за время коммутации, определяемое индуктивностью рассеяния вторичной обмотки.

При математическом описании трехфазного мостового выпрямителя [4] принято, что диоды вентильного коммутатора обладают нулевым сопротивлением в открытом и бесконечно большим сопротивлением в закрытом состоянии, а также мгновенным переключением из одного состояния в другое.

Тогда для математической формализации процессов в трехфазной схеме выпрямления удобно использовать понятие фазных коммутационных функций Fa, Fb, Fc [5], которые можно определить следующим образом: коммутационная функция соответствующей фазы равна +1 – если открыт четный вентиль; – 1 – если открыт нечетный вентиль; 0 – если оба вентиля заперты.

Анализ схемы выпрямителя с учетом данного выше определения фазных коммутационных функций показывает, что математическая связь между фазными напряжениями ua, ub, uc, токами ia, ib, ic сети и выпрямленным напряжением Ud и током id с помощью фазных коммутационных функций Fa, Fb, Fc определяется следующими соотношениями:

Ud ^а ' ^а + ¹¹ b ' ^Ь + ^*с ' ^с ,

^а ^a'^d’^b F_b • lj ,i_c F_c • ij .

Следует уточнить, что в уравнениях (3) и (4) фигурируют мгновенные значения соответствующих напряжений и токов, а паре диодов каждой фазы моста выпрямителя изоморфна соответствующая операция перемножения. Кроме силового коммутатора полная математическая модель неуправляемого выпрямителя должна содержать элемент формирования коммутационных функций.

Одним из возможных вариантов является их формирование путем сравнения аргумента α=ω∙ t сетевого трехфазного напряжения с его теоретическим значением в точке естественной коммутации - а _ек .

Второй вариант – это формирование фазных коммутационных функций путем сравнения мгновенных значений фазных напряжений Ua, Ub, Uc с расчетным значением напряжения U е_к в точке естественной коммутации.

Основное достоинство получаемых при этом моделей – их простота. Однако они не учитывают особенностей работы диодного выпрямителя при отклонении трехфазного напряжения от стандартных параметров (отклонение формы напряжений от синусоидальной, перекос напряжений по фазам и т. д.), когда U е_к и точка естественной коммутации а _ек смещаются относительно расчетного значения. Эти недостатки можно исключить, если фазные коммутационные функции формировать путем непосредственного сравнения мгновенных значений фазных напряжений. Очевидно, что в этом случае схема будет несколько сложнее, но это усложнение окупается точностью воспроизведения процессов выпрямления при всех реально возможных отклонениях параметров напряжения питающей сети от идеальных значений.

Если фазные коммутационные функции формировать путем непосредственного сравнения мгновенных значений фазных напряжений, каждое из них полезно разделить на два сигнала, состоящих только из положительных

*               **

Ua = ^а " ^b Ub = Ub • Fy, Uc = UC • Fy(5)

или отрицательных полуволн

Ua =ua'^2^^b = ^b‘^2’Uc =Uc-F2,(6)

где F 1 = 1 и F 2 = 0 при ui > 0, F 1 = 1 и F 2 = 0 при ui < 0. Здесь вместо индекса i принимается a, b , c для соответствующей фазы.

Такое разделение позволяет непосредственно использовать сигналы ,   , и ,,

U _c для вычисления коммутационных функций:

ра=р3^иа-иь-исур4\иа -ub -uc ),(7)

рь=р3^иь-иа-исур^иь -ua -uc ),(8)

Р^Рз^Щ-иь-и^ + Р^Щ -Ub -UQ ),(9)

где F3 = 1 и F4 = 0, если выражение в скобках больше 0, F3 = 0 и F4 = –1, если выражение в скоб ках меньше 0.

Совокупность уравнений (2)-(9) полностью характеризует процессы в неуправляемом трехфазном мостовом выпрямителе. Соответствующая им структурная схема показана на рис. 1.

На рис. 2 приведена структурная схема LC -фильтра звена постоянного тока ПЧ [5].

Здесь Ud , U и – входное и выходное напряжения фильтра; id , ic , i и – токи дросселя, конденсатора и нагрузки фильтра; Rd , Td , C – параметры фильтра [5].

Эта схема справедлива, если источник напряжения U_d имеет двустороннюю проводимость тока. Диодный выпрямитель таким свойством не обладает. Он может проводить ток только в одном направлении. Следовательно, при разработке математической модели звена постоянного тока это свойство источника напряжения U_d необходимо учесть, обеспечив соответствие воспроизводимых моделью процессов процессам реальным.

В реальной схеме при положительном значении Δ U = U_d – U _и ток i_d будет иметь положительное значение. При уменьшении Δ U вплоть до смещения в отрицательную область ток id также будет уменьшаться, приобретая нулевое значение со сдвигом (запаздыванием) во вре-

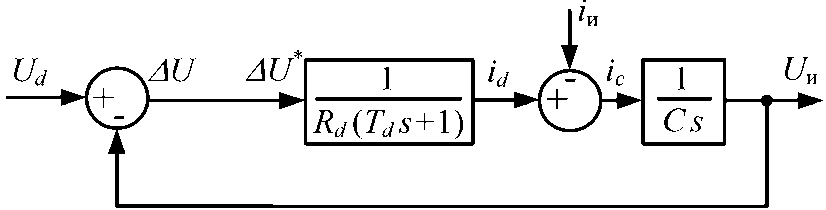
Рис. 2. Структурная схема LC -фильтра

Fig. 2. Structural scheme LC-filter мени относительно момента, когда ΔU изменит знак. В дальнейшем id остается равным нулю вплоть до момента, пока ΔU не вернется в положительную область.

Математически и структурно формализовать описанный алгоритм можно следующим образом. Будем различать (см. рис. 2) сигнал A U на выходе узла сравнения и сигнал на входе апериодического звена, обозначив последний AU* .

Сигнал Δ U^*, в свою очередь, будем рассматривать как сумму двух сигналов:

м/ = ш₊ + мГ ,                                    (10)

где A U + = A U при A U > 0, A U + = 0 при A U < 0.

Напряжение определим выражением

MJ^MJ.-FQ^ ,                                   (11)

где A U _- = 0 при A U > 0, A U _- = A U при A U < 0.

Функция F(id) учитывает знак id - F(id ) = 1 при id > 0, F(id ) = 0 при id <  0.

Доработанная с учетом уравнений (10) и (11) структурная схема силового фильтра показана на рис. 1. Она полностью учитывает специфику процессов в фильтре звена постоянного тока при включении его на выход диодного выпрямителя.

Вентильный коммутатор автономного инвертора напряжения при представлении вентилей идеальными ключами - это обращенный вентильный коммутатор трехфазного выпрямительного моста [5], у которого входное постоянное напряжение питания U и поступает на клеммы постоянного тока, а выходными являются фазные переменные напряжения Ua , Ub , Uc .

Воспользовавшись введенным ранее для выпрямителя понятием фазной коммутационной функции, связь между переменными вентильного коммутатора АИН можно выразить следующими соотношениями [5]:

?/(,=и„(2Г,/3-^/3-Тс/3)/2,

(/,, =(/„(2/-,,/3-Л,'3-/;./3)/2,

UC=U,\2FCJ3-Fh B-FJ 3^2, i — i F + i F + i F , где Uи, iи - входное напряжение и ток вентильного коммутатора АИН; Ua, Ub, Uc, ia, ib, ic - фазные выходные напряжения и токи вентильного коммутатора; Fa+, Fb+, Fc+ - положительная полуволна соответствующих фазных коммутационных функций Fa, Fb, Fc.

В отличие от диодного выпрямителя, где коммутационные функции формируются естественным образом за счет непрерывного сравнения мгновенных значений фазных напряжений и включения диодов в точках естественной коммутации, в автономных инверторах для формирования коммутационных функций требуется специальная система управления ключами инвертора, позволяющая формировать желаемые амплитуду и частоту выходного напряжения. Возможность одновременно формировать амплитуду и частоту выходного напряжения достигается использованием широтно-импульсной модуляции входного напряжения автоном-– 96 – ного инвертора. Существует достаточно много законов и алгоритмов реализации широтноимпульсной модуляции.

Положив, что на входе системы управления силовыми ключами инвертора действуют сигнал U _ymax , определяющий амплитуду первой гармоники выходных напряжений АИН, и гар-

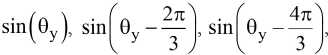
свя-

монические сигналы (координатные функции занные с мгновенным значением частоты первых гармоник этих напряжений соотношением 0у = УуО)(/)с//, фазные коммутационные функции Fa, Fb, Fc, определяющие алгоритм работы ключей каждой фазы коммутатора АИН, формируются путем сравнения соответствующих сигналов управления

Uya = ^утах^п(Оу), т г тт "ГаЛ у/, — ' ymax s 1111 Оу ~ I,

. (4 л ус ^ymax^l^Oy с опорным сигналом Uг генератора пилообразного напряжения.

Структурная схема АИН с ШИМ, состоящая из структурных схем вентильного коммутатора и описанной выше системы формирования коммутационных функций, приведена на рис. 1.

Разработанная математическая модель ПЧ реализована в пакете Simulink MATLAB .

Для численных расчетов приняты следующие параметры питающей сети: действующее фазное напряжение U ф = 220 В, частота напряжения f = 50 Гц.

Использованы параметры разделительного трехфазного трансформатора ТСЗР-10380/380, приведенные к вторичной обмотке: R 1 = 0.2 Ом, 1Т 0.6 Ом, R_m = 78 Ом, L 1 = 6 • 10 ^-6 Гн, /,₂ 9 ■ 10 ⁶ Гн, L_m = 1.9 Гн. Параметры нагрузки: R _н = 22 Ом, L _н = 0.01 Гн. Генератором пилообразного опорного напряжения U г задан период дискретизации ШИМ 0.001 с.

Результаты исследований свидетельствуют о том, что разработанная модель как качественно, так и количественно отображает процессы, протекающие в реальном ПЧ. Это иллюстрируют графики изменения переменных в звене постоянного тока (рис. 3, 4) и переменных в нагрузке (рис. 5) при моделировании режима прямого подключения преобразователя с активно-индуктивной нагрузкой к сети.

Как видно на графиках, в начальный момент включения наблюдается значительная просадка напряжения U_d (рис. 3) на выходе выпрямителя, обусловленная ограниченной мощностью питающей сети (трансформатора), и бросок тока дросселя (рис. 4), значительно превышающий установившееся значение. Для ограничения броска тока необходимо применение специальных мер, например предварительный заряд конденсатора фильтра от внешнего источника с большим внутренним сопротивлением.

В установившемся режиме во всех переменных звена постоянного тока наблюдаются низкочастотные колебания с тройной частотой тока нагрузки (рис. 5) преобразователя частоты. Это также объясняется потерями в трансформаторе и дросселе силового фильтра.

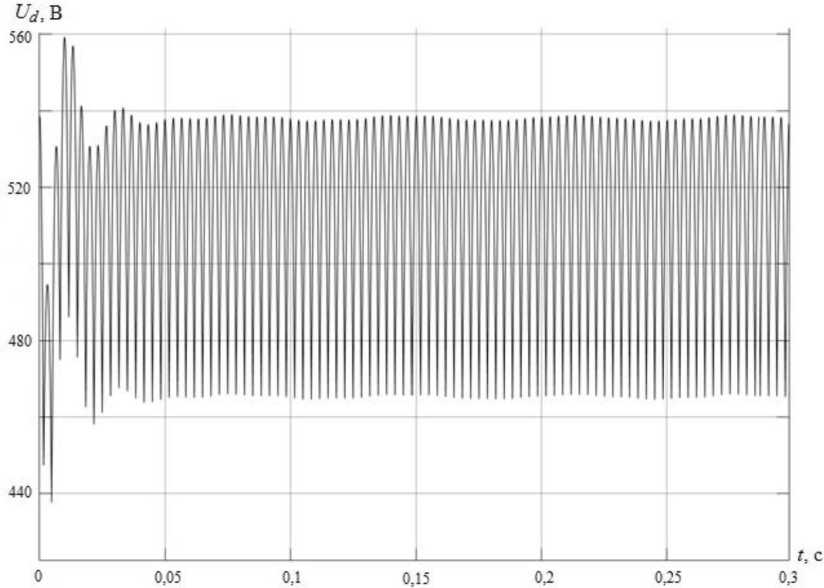
Рис. 3. Графики изменения выпрямленного напряжения U_d

Fig. 3. Graphs change straightened voltage U d

id A

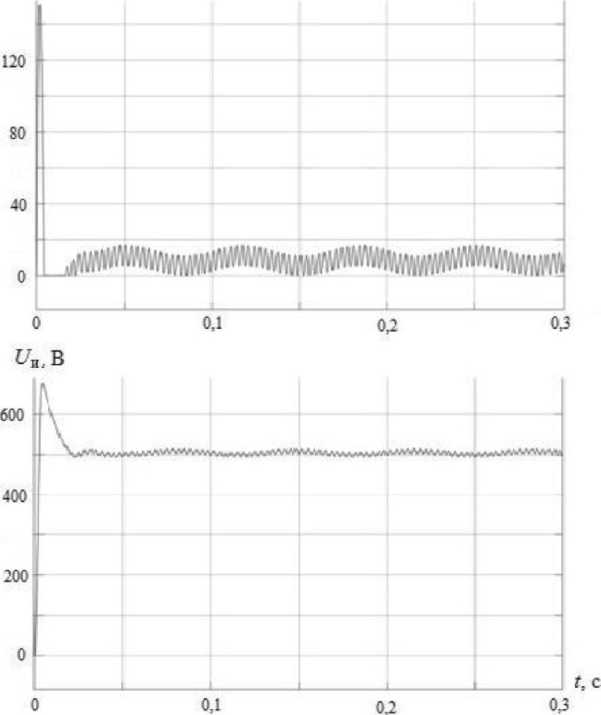
Рис. 4 Графики изменения тока дросселя i_d и напряжения инвертора U _и

Fig. 4. Graphs change throttle current i d and inverter voltage U и

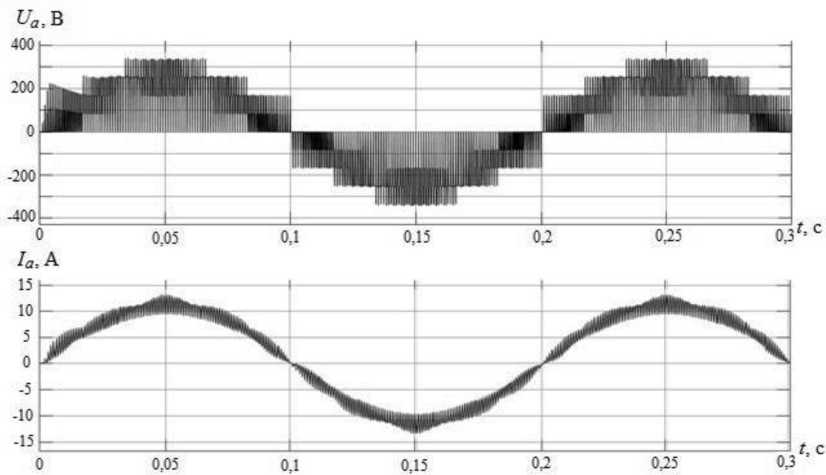
Рис. 5. Графики изменения напряжения U a и тока I a в нагрузке фазы А

Fig. 5. Graphs change voltage U a and current I a in phase load А

Все графики получены при задании амплитуды и частоты первой гармоники выходного напряжения ПЧ 220 В и 5 Гц соответственно.

В заключение следует отметить, что использование теории индукционных устройств и понятия коммутационных функций позволило на единой методологической основе создать физически и математически обоснованные математические модели всех основных элементов преобразователя частоты.

Кроме того, применение метода структурного моделирования дало возможность получить достаточно универсальную гибкую модель ПЧ в целом, сохранив топологию реального преобразователя частоты и наблюдаемость всех его реальных физических переменных. Построенная модель ПЧ позволяет прояснить взаимосвязи между физическими переменными отдельных элементов ПЧ и их взаимное влияние.

Применение при построении моделей натуральных систем координат помогло сохранить соответствие (изоморфность) наблюдаемых модельных переменных их реальным аналогам и, как следствие, наблюдать их без дополнительных координатных преобразований. При этом прояснилась математическая сущность выпрямителя и автономного инвертора как прямого и обратного координатных преобразователей.