Математическая модель прессования плит на основе измельченной соломы и термопласта

Солома хлебных злаков относится к отходам переработки сельскохозяйственных культур. Однако при измельчении и прессовании совместно с другим бытовым отходом – вторичным полиэтиленом – она может стать очень дешевым сырьем для нового композиционного материала высокого качества. Плиты из данных материалов имеют высокую прочность, водостойкость, обладают высокими тепло- и шумоизоляционными свойствами и могут найти применение в производстве мебели, строительстве и т.д.

Солома зерновых культур имеет низкую насыпную плотность. Плотность измельченной соломы пшеницы с длиной частиц от 2 до 10 мм составляет 65 кг/м3. Частицы полиэтилена, получаемые в результате измельчения резанием выброшенных в мусор бытовых мешков, имеют следующие размеры: длина 2–5 мм, ширина 1–2 мм, толщина 0,02–0,05 мм. Насыпная плотность полиэтилена составляет 0,184 г/см3, температура плавления полиэтилена низкого давления лежит в пределах 125–137 0С [1]. При использовании специальной технологии из данных компонентов может быть получен композиционный материал, представляющий собой устойчивую двухфазную систему, в которой армирующим наполнителем служат частицы соломы, а связь структурных элементов осуществляет термопласт в виде вторичного полиэтилена.

Формирование плит из частиц измельченной соломы и термопласта сопровождается протеканием сложных физических процессов, математическое моделирование которых позволит получить требуемые конечные свойства готовых плит. Смесь компонентов прессуют, в этом случае процессы прессования и нагрева совмещены в одном технологическом цикле.

Главную роль в образовании структуры исследуемого материала играет напряженнодеформационное состояние термопластов в процессе их преобразования в клеевую прослойку. Компоненты плит имеют различные физико-механические и теплофизические характеристики, поэтому при расплавлении и застывании полимерной матрицы возникают напряжения, превышающие предел прочности отдельных компонентов. Неправильный выбор технологических параметров значительно ухудшает качество композиционных материалов. Оптимальные режимы изготовления и наилучшие свойства композита можно получить за счет моделирования процессов формирования композитов, совместно с аналитическими оценками эффективных свойств исходных материалов.

Плитные из частиц соломы и термопластов получают методом плоского прессования с контактным нагревом, который производят снизу и сверху.

При выполнении условия δ <<  l (рис. 1) процесс переноса энергии можно рассматривать в одномерной постановке, считая, что начальное распределение температуры по толщине δ равномерное.

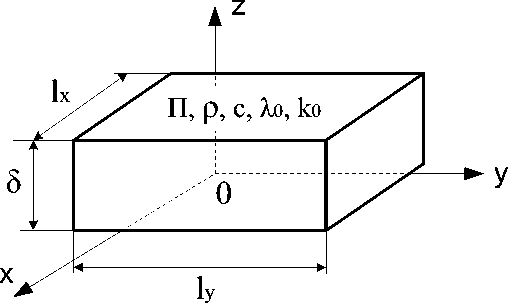
Рис. 1. Расчетная схема модели прессования

Анализ гидродинамических характеристик исходных пакетов показал, что они обладают ограниченной проницаемостью. Пакеты проницаемы при температуре Т <  348К и давлении прессования Р пр < 1,5 МПа. Проницаемость рассматриваемых пакетов вне указанных значений давления и температуры стремится к 0 (непроницаемые). Эти особенности были учтены при разработке мамодели процесса прессования плит из частиц соломы на основе термопластов. Рассмотрим эти особенности, используя методику [2].

Содержание влаги в пакете не превышало 7 %. Его прогрев начинался при температуре около 350K. Именно при достижении этой температуры начинается размягчение полимера, после чего пакет становится непроницаем. С этого же момента начинается процесс обволакивания частиц соломы полимерной матрицей. Таким образом, массоперенос в предшествующем этому моменту обусловлен только фильтрацией воздуха, находящегося в порах пакета.

Плотность воздуха в 700 раз меньше плотности прессуемых пакетов (около 900 кг/м3), поэтому влиянием массопереноса при фильтрации воздуха на температуру пакетов пренебрегаем. Тогда в уравнении переноса энергии должен учитываться лишь объемный источник энергии, обусловленный тепловым эффектом процесса затвердевания полимерной матрицы [2]. В этом случае уравнение переноса энергии будет иметь вид

∂Т с⋅ρ⋅     =⋅

∂t   ∂z

⋅ ∂ ^T ) ± I VT , ∂ t

где с – удельная теплоемкость, кДж/(кг ⋅ К);

ρ – плотность, кг/м3;

Т – температура, градус К;

λ 0 – коэффициент теплопроводности, Вт/(м ⋅ К).

I VT – объемный источник теплоты, обусловленный тепловым эффектом затвердевания термопласта.

В процессе затвердевания частицы полиэтилена забирают энергию, которую имеет расплавленный полиэтилен.

Так как проницаемость и физические свойства прессуемого пакета меняются в процессе прессования, формула переноса энергии (1) должна быть дополнена кинетическим уравнением отверждения полимерной матрицы (2) и уравнениями термовязкоупругости (3) и (4).

=(θk -θ)n ⋅ К(T) ⋅C0n-1,

р-вт

ад = — х :- 1 ( - 1) τ

n + 1 (Y • Г(а))

-n г Т уа

Г(п • a) I О J

,

где р , у , а - экспериментально определяемые параметры материала;

Г = 1, гамма-функция согласно [2];

n – количество членов суммы ряда;

Ө k – конечная степень отверждения связующего;

К(Т) – показательная функция [2];

n – количество членов суммы ряда [2];

т - задаваемая продолжительность процесса.

t

A

E^(t) = E ^U + j ^K(t - ^TM^T)d^T , к -®                J

где e (t) - реакция композиционного материала во времени;

с ( т ) - внешнее силовое воздействие.

Соответствующие уравнениям (2)–(4) ядра и резольвенты должны соответствовать условиям [2].

Функция температурно-временного сдвига

1па т (Т - T o ) = {

k 1 • (T - T₀), 273K <  T <  373K;

k2,

Т >  373K,

где Т 0 – температура среды;

а _т - коэффициент, определяющий свойства исходных материалов;

k 1 = 0,025, k 2 = 2 – коэффициенты сдвига пакета.

Совокупность уравнений (2)–(5) представляет собой математическую модель процесса изготовления плит из частиц соломы и термопластов.

Рассмотрим кинетику затвердевания полимерной матрицы. Скорость химической реакции затвердевания зависит от температуры и количества термопласта в смеси и описывается уравнением

- dC = k(T) • Cⁿ , dt

а степень реального взаимодействия связующего с частицами соломы описывается выражением

С-С

О = ^C C

C 0

,

где С 0 и С – соответственно начальное и текущее содержание взаимодействующего термопласта, кг/кг.

Температурную зависимость скорости реагирования для термопластов, по аналогии со скоростью отверждения термореактивных смол, опишем уравнением Аррениуса

^k(T) = ^k 0 • ^exp^{( -} ^U) , RT

где k 0 – константа скорости затвердевания, 1/с.

Подставляя (7) в (6), получим окончательное уравнение кинетики затвердевания полимерной матрицы ddθt =(θk -θ)n ⋅k(T) ⋅C0n-1 ⋅exp(-RUT),                   (9)

где U – энергия активации, имеющая положительное значение.

В уравнении (9) параметры n , k 0 , U подлежат экспериментальному определению для каждого типа термопласта.

Очевидно, процесс затвердевания сопровождаются выделением или поглощением теплоты. Тепловой эффект реакции, обусловленный перераспределением химических связей и изменением межмолекулярных взаимодействий, принимаем за показатель степени затвердевания термопласта. Конечная степень затвердевания описывается выражением

_{θ =} ^Q отв ^{⋅ M}

k ± ΔH ⋅ C0 , где М – молярная масса реагирующих веществ, кг/моль;

Q отв – теплота застывания термопласта, Дж;

ΔН – теплота, необходимая для протекания процесса (в случае затвердевания знак минус).

Степень затвердевания термопласта опишем уравнением кинетики отверждения полимерной матрицы [4], в следующем виде:

^d _d ^θ _t = (1 - θ)ⁿ ⋅ exp k ^∗ 0 ( - _R ^U _T) ,                         (11)

где k 0 – множитель, определяющий размерность d θ /dt.

Методы определения параметров, входящих в уравнения (9) и (11), изложены в [5]. Например, объемный источник энергии, обусловленный тепловым эффектом реакции затвердевания, может быть описан уравнением

± ΔH        ∂ θ

I VT = M ⋅ a 2m ⋅ ρ ⋅∂ t ,                               (12)

где ρ – плотность отвердевающего вещества, кг/м3, a 2 m – массовая доля полимерной матрицы в композите, кг/кг.

Для однозначного решения уравнений, входящих в математическую модель, необходимо сформулировать краевые условия, которые должны соответствовать [2].

Связь между деформацией, плотностью и пористостью композиционного материала в процессе прессования устанавливается соотношениями:

1 ^ρ = ^{ρ 0n} ⋅ 1 - ε(t ′ )

П = 1 - ρ ρk .

где ρ 0n – начальная плотность исследуемого композита;

П – пористость исследуемого пакета;

ρ k = ρ 1 ⋅ c 1 + ρ 2 ⋅ c 2 – плотность композита без учета пористости.

с 1 , с 2 – удельные теплоемкости компонентов пакета.

tI – температурная координата.

В экспериментах накладываемые на полученные оценки факторы были увязаны со свойствами композиционного материала. Компоненты перемешивались вручную до однородного состояния, отсыпались в форму размерами 235 × 250 мм высотой 15 мм и подпрессовывались до высоты 10 мм. Горячее прессование производилось под давлением 0,15 МПа при температуре 473К, причем продолжительность выдержки плит из соломы и полиэтилена составляла 8 мин, из соломы и полипропилена – 16 мин. Затем в течение 3 часов плиты остывали до t = 100^оС в зажатом состоянии, пресс размыкался, образцы выдерживались до полного остывания (20^оС) в течение суток, после чего производилось испытание их физико-механических свойств.

Как показали дальнейшие измерения, данные условия реализуют физико-механические характеристики плитных материалов в наилучшей степени.

Энергия деформирования при прессовании определяется из уравнения

W = — fa- • £й • dV

2 ij ij ,

V

где σ ij – силовое воздействие по двум направлениям;

ε ij – реакция композиционного материала по соответствующим направлениям;

V – объем пакета.

Энергия деформирования может быть использована в качестве критерия, при выполнении которого свойства компонентов наилучшим образом будут реализованы в плитном материале, т.е. будет сформирована оптимальная структура с комплексом наилучших физико-механических показателей. Это связано с тем, что в процессе прогрева пакета полимерное связующее плавится и происходит его затвердевание. Модуль Юнга затвердевающего полимера нарастает, растет также прочность материала, а деформация в соответствии с уравнением (4) убывает. Энергетический критерий (15) также убывает.

При уменьшении модуля Юнга критерий (15) будет возрастать. Поэтому данный критерий имеет экстремум, в точке которого свойства компонентов реализуются наилучшим образом.

В одномерном случае критерий (20) имеет вид

^W = 7 J ° z • ^s(z) • ^dV .

V

При достижении критерием (16) минимального значения с учетом обеспечения требуемой плотности, определяемой по уравнению (13), процесс прессования должен быть завершен.

Заключение

На основе уравнения переноса энергии в композиционном материале, кинетического уравнения отверждения полимерной матрицы и уравнения термовязкоупругости представлена математическая модель процесса прессования рассматриваемого плитного материала.

В результате численной реализации на ЭВМ математической модели процесса прессования материалов при заданных краевых условиях количественно оценены такие параметры, как проницаемость исходных пакетов, распределение по толщине плиты температуры, степень затвердевания термопласта, а также термические напряжения, возникающие при кондиционировании получаемых плитных материалов. Однако без определенных ограничений, данные оценки являются чисто информативными и не могут быть использованы в качестве обратных связей в моделях управления.

Установлен критерий, согласно которому следует завершать прессование. При этом структура плитного материала достигает оптимума.