Математическая модель привода главного движения пилорамы

Введение. Важнейшим звеном в лесопильном производстве являются лесопильные рамы. Их существенным недостатком являются неуравновешенные силы инерции подвижных масс кривошипно-шатунного механизма, вызывающие вибрацию. Для анализа явлений, происходящих в механизме пилорамы и оценке технологического процесса, представляется возможным использование теории регулярных колебательных систем [1], основываясь на теории цепочек, позволяющей аналитически исследовать динамические характеристики систем с большим числом степеней свободы, базируясь на анализе одного структурного элемента [2-6].

Исследование процесса силового взаимодействия при распилке лесоматериала на пилорамах неизбежно сводится к построению математической модели механизмов, формообразующее движение которых и приводит к его образованию. Одна из парциальных систем пилорамы совершает неравномерное программное движение, имеется в виду кривошипно-шатунный механизм привода рамы. Кроме того, на этот привод накладываются нежелательные колебания, вызванные кинематическим возбуждением. Согласно многочисленным работам по этой теме, особенно значительные динамические ошибки возникают из-за виброускорений [1, 6]. Одной из основных задач в снижении виброактивности, а соответственно и уровня акустической эмиссии исследуемого процесса, является обеспечение требуемого закона движения (гармонического) инструмента. Таким образом, особое значение представляет исследование формообразующих движений. При исследовании динамики упругих элементов машин и механизмов, как правило, предполагается, что влияние вынуждающих колебания устройств одностороннее, т.е. отсутствует обратное влияние упругой подсистемы на источник энергии.

Целью настоящей работы является создание математической модели привода главного движения пилорамы, которая и позволит решить все указанные выше задачи.

Построение математической модели привода главного движения пилорамы. Рассмотрим механизм привода пилорамы, представляющий собой последовательно соединённую ремённую передачу, и кривошипно-шатунный механизм, который реализует кинематическую функцию положения ведомого звена.

Рассматриваемый механизм относится к классу устройств, преобразующих вращательное движение приводного вала в неравномерное движение рабочего органа. В таком случае зависимость, связывающая положение ведомого звена с углом поворота приводного электродвигателя, является нелинейной. Анализ кинематической схемы исследуемого механизма позволяет сделать вывод, что динамическая модель пилорамы может быть классифицирована как неголономная система из-за наличия ремённой передачи. Однако при этом нужно учитывать возможность проявления параметрических резонансов, так как приведённый момент инерции механизма также является функцией φ .

В этом случае динамическая модель исследуемого объекта представлена в виде расчетной схемы (рис.1).

Md

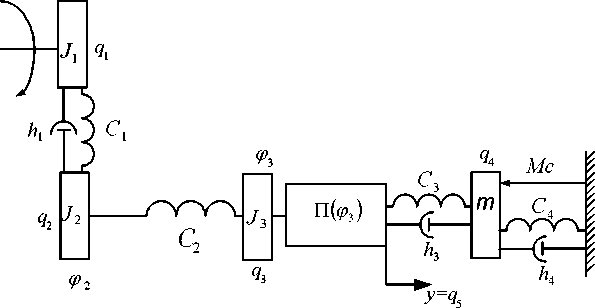
Рис.1. Расчётная схема привода пилорамы

Так как звенья этого механизма совершают сложное плоское движение в вертикальной плоскости, необходимо учитывать работу сил тяжести. Кроме того, в механизме имеется звено, совершающее плоскопараллельное движение. Для таких звеньев, согласно [4], инерционные характеристики могут быть приведены к звеньям, совершающим вращательное и поступательное движения, т.е. к кривошипу и раме. Используя метод замещения масс, получим:

L

Δ J ₃ = m_ш ⋅ ⋅ R ² ;

3 ш 2    3

L

Δ m = m_ш ⋅ ₂

.

Электромеханическая система не может быть описана адекватной моделью без учёта инерционности процессов, протекающих в двигателе [3]. Уравнения, описывающие движения асинхронного электродвигателя, имеют вид:

dΨ1x dt dΨ1y dt dΨ2x

= U 1 x

-

r L' W r L W r1 ⋅ L2 ⋅ Ψ1x + r1 ⋅ L0 ⋅ Ψ

2 x

+ 0 Ψ 1 y ;

ΔΔ r ⋅ L ′ ⋅ Ψ      r ⋅ L ⋅ Ψ

1 2 1 y + 1 0 2 y -Ω ⋅Ψ ;

Δ            Δ         0    1x r2⋅L1⋅Ψ2x +r2⋅L0⋅Ψ1x +(Ω0 -Ω)⋅Ψ2y; t dΨ     r′⋅L ⋅Ψ    r′⋅L ⋅Ψ

2 y =- 2 1 2 y + 2 0 1 y - ( Ω -ω ) ⋅ψ ;

dt           Δ            Δ          ^{0         2 x}

= U 1 y

-

-

-

-

¹ _p ⋅ t ;

-

U _{1 y} = 2⋅ U_m ⋅sinω _p ⋅ t ;

dω= 3⋅Zp ⋅ L0 ⋅ Ψ ⋅i -Ψ ⋅i - 1 ⋅M , dt 2 J ⋅∆ ( 2x 1y 2y 1x) J C, где Z p – число пар полюсов электродвигателя; Ψ1x – проекция потокосцепления обмотки статора на ось x ; Ψ1y – проекция потокосцепления обмотки статора на ось y ; Ψ2x – проекция потокосцепления обмотки ротора на ось x ; Ψ2y – проекция потокосцепления обмотки ротора на ось y ; J – сумма момента инерции ротора электродвигателя и шкива; Ω0 – угловая частота вращения поля статора; Ω – угловая частота вращения ротора; ωp – угловая частота.

Таким образом, исследуемая электромеханическая система включает в себя электродвигатель, описываемый системой нелинейных дифференциальных уравнений первого порядка, а так- же системой уравнений, описывающих механическую часть привода. Для подобных задач обычно используют особую форму уравнений Лагранжа II рода с «лишними» координатами (их ещё на- зывают уравнениями Феррерса) [1, 2, 6]. Для рассматриваемого случая имеем:

d(dT A  d T  SP

n

= Qk ■ T ' a ■

= 1

( k = 1,..., s ) ;

I1

^dt ( ^{d q}k ) ^d 4 k   ^d 4 k

s

T a jk q k ⁺ a j = 0,      ( j = V-, n ) .

k = 1

Обобщённые координаты выбираем, пользуясь рекомендациями, приведенными в работе [6]. Задаёмся абсолютной координатой, соответствующей перемещению в начале кинематической цепи ф1 = q1, и далее вводим координаты, двигаясь по кинематической цепи. Выпишем основные кинематические соотношения:

ф 1 = О. t = q i ;

^ф 2 = ^ф 1 i 1 ⁺ q 2 = q i i 1 ⁺ q 2 ;

^ф з = ^ф 1 • i 1 ⁺ q 2 ⁺ q з = q 1 i 1 ⁺ q 2 ⁺ q 3 ;

^Y = ^{п ( ф} з ) = ⁿ( q 1 i ⁺ q 2 ⁺ q 3 ) ;

Z = Y + q 4;     Z = q 5 + q 4, где О - угловая частота вращения приводного электродвигателя; ф1, ф2, ф3 - угловые координаты соответствующих сечений в абсолютном движении; Y — абсолютная координата массы m. Последнее замечание означает, что в качестве обобщённых координат, за исключением q1 , приняты относительные координаты, отвечающие за деформацию упругих элемен- тов.

Уравнение связи запишем исходя из условия, что Z является функцией положения [1, 6].

П ( q 1 i 1 + q 2 + q 3 ) — Z = П ( Ф 3 ) — Z = 0.

Продифференцируем это выражение по времени:

п' q₁ i₁ + П' q₂ + П' q₃ — Z = 0.

В качестве «лишней» координаты примем Y = q 5 . Число степеней свободы исследуемой системы H = 4 , число «лишних» координат n = 1 .

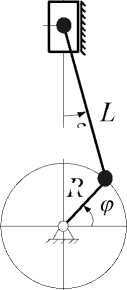
δ

R

Рис.2. Кривошипно-шатунный механизм пилорамы

В связи с тем, что рама с пилами движется в вертикальной плоскости (рис.2), её перемещение удобно представить в следующем виде: S max = L + R .

S = L • cos 8 — R • cos ф .

Общий катет прямоугольников ОАС и АВС определяет-(n A       R ся равенством вида: sin8 = ^.sinI— — ф1, где ^ = — .

П ( ф ) = S = L • cos 8 + R • sin ф — V L — R ;

П ( ф ) = L • -^ 1 — ^ • cos ф + R • sin ф — V L — R .

После преобразования имеем:

dS          d 8

= — L sin 8.   + R cos ф;

d ф         d ф d2 S         d 25      Л d 5)

—2- = -L sin 5--2 - L cos 5 • I I - R sin d ф          d ф         к d ф J

—(sin 5) = — (ck sin ф) = -c• sin ф; d фV } d ф d 5                           d 5      sin ф cos o = -C' sin ф или =-c • d ф                         d ф

‘            d 5

П ( ф ) = - L • sin 5 + R • cos ф = L •c---sin 5 + R • cos ф;

d ф d f d5     _)

• cos 5 =     ( -C'sin ф ) ;

dф(dф     J dф’ d 25    s f d 5)

—7 • cos 5-       • sin 5 = -c• cos ф;

d ф²        к d ф J

(

d ²5 d ф²

cos 5

c2' к

2 sin ф ) cos 5 J

)

-C'cosф ;

J

d 2 S    . . „ d 25  T    J d5 П ( ф ) = —7 = - L sin5-- 7- L cos5 — v ’ d ф 2              d ф 2           к d ф, f      ;„a>2         ) ± \ т sin5      2 1 sinф )                             I П (ф) = L • s• c •! s I c'cos ф L cos 5 •I cos 5 к   к cos 5 J           J

J - R cos ф; " sin ф) 2 С _ I R • cos ф. 4 cos 5 J

Проведём оценку спектра координаты Y с целью выявления частот возбуждения механизма механической частью привода. С этой целью проведем расчёт с использованием возможностей системы Mathcad (рис.3):

R := 0.3 - радиус кривошипа;

L := ² - длина шатуна;

n := 325 ;

_q ■= 2• _n • — = 34 034 - угловая скорость кривошипа; 60^.

Z ■= L = 0.15 - отношение длин кривошипа и шатуна;

k ■= 1.. 1000 ; t k ■= 0.0005^k ; ^ф k ■= ^q • t k ; 5^ ■= asin ^f z • sin^fy - ф _k ⁾⁾ ;

n k ■= L• U 1 - z • cos ( ф k ) + R• sin ( ф k ) ) - L ;

n 1 k ■= L• z ^

sin(ф k) cos(°k)

• sin ( s k ) + R• cos ( ф k ) ;

^sin( s k ) n 2 k ■= L

cos(s k)

2 f ^{Sin (}Ф k )

Z к cosl5^)

J

- Z •cos ( ф k )

- L• cos ( s k ) •

f ^sin( ф k ) ) ²

VZ cos(5k)j

- R• cos ( ф k ) .

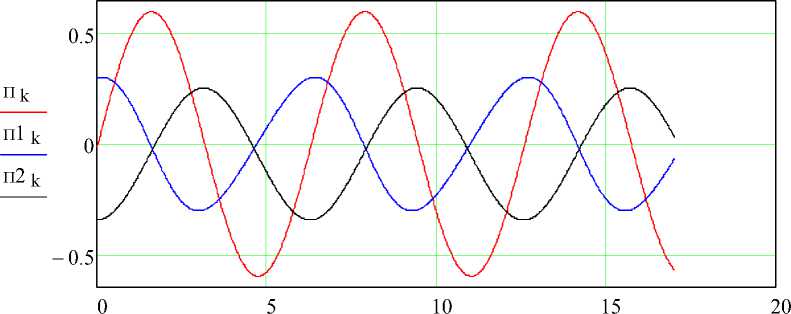
ф k

Рис.3. Соотношение выходного смещения нелинейного звена, его скорости и ускорения от угла поворота ведущего звена

Проведём Фурье-анализ с использованием системы Mathcad (рис.4).

Как видно из анализа полученных графиков, наличие кратных гармоник просматривается, в наличии фазовые сдвиги, отличные от ^2 . Последнее означает, что можно ввести некоторые упрощения в систему уравнений динамики механизма.

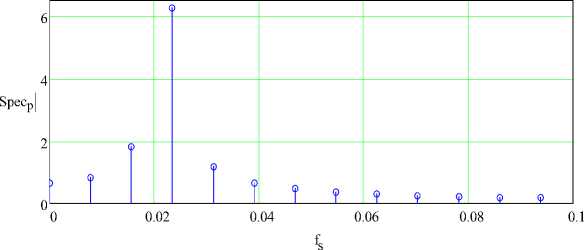
p —

N0

Рис.4. Фурье-спектр выходной координаты нелинейного элемента

Для составления математической модели механической части привода пилорамы выражаем кинетическую и потенциальную энергию через принятые обобщённые координаты, включая и «лишние»:

2T = J 1 ф 2 + J ₂ф 2 + J 3 ф 2 + m • Z ²;

2 P = C 1 ( Ф 2 -Ф 1 ) ² + C 2 ( Ф з -ф₂ ) ² + C 3 • ( Z - Y ) ².

Диссипативная функция системы (функция Релея):

2Ф = h 1 ( ф₂ -ф 1 ) + h ₂ ( ф₃ -ф₂ ) + h 4 Z: 2.

Выражение для виртуальной работы может быть записано в виде:

5 A = Md • 5 q, -F„₇ •б Z -b • q ₂ •б q₂ - b.Z: •б Z ,

1 pez             2    2      2      4

где b ₂ – приведённый коэффициент линейного демпфирования привода и ведомого звена, полученный путём эквивалентной линеаризации диссипативных сил [1, 4, 6]; b ₄ – коэффициент вязкого трения при резании.

Запишем выражение кинетической энергии с учётом кинематических соотношений:

2T J 1 < д + J 2 ⁽ < 1 i i + < 2 ) ⁺ J 3 ⁽ < 1 i i ⁺ < 2 ⁺ < 3 ) ⁺ m * ⁽ < 4 ⁺ < 5 ) ;

^{2 T} — J 1 <7 i + J 2 ( <7 i i i + ² i i q i < 2 + < 2 ) + J 3 ( <7 i i i + ² i i q i * ⁽ < 2 + < 3 ) + < 2 + < 3 + 2 2 < 3 ) + m * ( < 5 + 2 < 4 < 5 + < 4 ) ;

2 T — <7 i ( J 1 + J 2 i i + J 3 i i ) + < 2 ( J 2 + J 3 ) + < 3 J 3 + 2 < i < 2 ( J 2 i i + J 3 i i ) + 2 < 2 < 3 J 3 +

+2 < _i 3 i_i J ₃ + m< ₅² + 2 т<₄< ₅ + m< 2 .

Исходя из матричного представления кинетической энергии системы 2 T — q T * M * q и того, что коэффициенты при обобщённых скоростях постоянны, инерционные коэффициенты приравниваем к соответствующим коэффициентам квадратичной формы, представляющей кинетическую энергию системы, получим матрицу инерционных коэффициентов в виде:

	" J i + J 2 i i + J 3 i i	J 2 ii + J 3 ii	J 3 i 1	0
M —	J 2 i i + J 3 i i	J 2 + J 3	J 3	0
	J 3 i 1	J 3	J 3	0
	_         0	0	0	m

Согласно работам [1, 4] необходимо рассматривать отсчёт потенциальной энергии от положения устойчивого равновесия P ( 0,0,...,0 ) — P |0 — 0 . Кроме того, считаем, что все связи стационарны, процесс резания рассматривается не как составляющая механизма, а как внешнее воздействие. Если же принять, что передаточное отношение не зависит от скорости звеньев, матрица жёсткостей аппроксимирующей системы дифференциальных уравнений исследуемого объекта может быть принята постоянной [4].

2 P — C i ( ф₂-ф 1 ) 2 + C 2 ( Ф 3 — ф₂ ) 2 + C 3 ( Z — Y ) ²;

^{2 P — C} 1 ⁽ < 1 ⁽ i i ^{— 1) +} < 2 ) ^{+ C} 2 ⁽ < 1 i i ⁺ < 2 ⁺ < 3 ^— < 1 i i < 2 ) ^{+ C} 3 ⁽ < 5 ⁺ < 4 ^— < 5 ) ’

2 P — < 2 * C ₁ * ( i₁ — 1 ) + <₁ ^q ₂ C ₁ ( i₁ — 1 ) + < 2 * C ₁ + < 2 * C ₂ + < 4 * C 3 .

Исходя из матричного представления потенциальной энергии системы 2 P — q ^T * C * q и того, что жёсткости связей постоянны, коэффициенты матрицы жёсткостей получим приравниванием соответствующих коэффициентов квадратичной формы, представляющей потенциальную энергию системы, в виде:

"C1*(ii —1)2   Ci .(/'1— 1)    0    0

C — C1*(ii—1)       Ci        0    0

0          0      C2

_     0            0       0   C3

В выражение потенциальной энергии вошла координата X , но хотя она посредством нелинейной функции П ( ф₃ ) жёстко связанна с координатой < ₃ , изменение потенциальной энергии исследуемой системы определяется перемещением инерционных масс в вертикальной плоскости [1, 4, 6].

Представим функцию демпфирования в матричном виде:

2Ф — h i ( ф 2 —ф 1 ) 2 + h 2 ( ф 3 —ф 2 ) 2 + h 3 ( Z 7 — Y ⁷ ) 2 ;

^{2 Ф —} h i ( < ( i i ^{— i} ) ⁺ 2 ) ^{2 +} h 2 ( i ⁺ 2 ⁺ 3 ^— < 1 i i <1 2 ) ^{2 +} h 3 ( 5 ⁺ 4 — 5 ) ² ;

2Ф = <7 2 • h • ( i₁ -1 ) 2 + <7 2 • h + 2 • h ₂ + h 3 • q ₃² + 2 q ₁ <7 2 • ^ ( i₁ -1 ) .

Исходя из представления матрицы демпфирования в виде 2Ф = q T • H • q , получим матрицу H :

	■ h l • ( i l - 1 ) 2	h l • ( i l - 1 )	0	0
H =	h l • ( 4 - 1 )	h 1	0	0
	0	0	h 2	0
	_      0	0	0	h 3

Обозначим диссипативные силы R_k , сохранив нумерацию, принятую для упругих элементов. В данном случае R ₁ – момент диссипативных сил в ремённой передаче, R ₂ и R ₃ – момент диссипативных сил, связанных с внутренним трением в валах. Моментами сил трения в опорах пренебрегаем [1, 6]. Дальнейшие действия сводятся к записи системы дифференциальных уравнений движения и исключению множителей Лагранжа [1, 6]. Полное число уравнений равно H + n = 5 . В первой части, помимо обобщённых сил, стоит слагаемое Л a₁ j , так как n = 1 . Запишем уравнения, устанавливающие связь «лишних» и независимых координат.

Определим коэффициенты уравнений дополнительных связей:

Y = q ₅ = ^п( ф ) = ^п( q i i i + q 2 + q 3 ) ;

<7 5 = П ( ф₃ ) • q ₁ i₁ + П ( ф₃ ) • <7 2 + П ( ф₃ ) • q ₃ или П ( ф₃ ) • q ₁ i₁ + П ( ф₃ ) • q ₂ + П ( ф₃ ) • q₃ - <7 5 = 0.

Общий вид уравнения связи:

H + n

^ a k a k + a l = 0 , k = 1

где H + n = 5 .

Сопоставим полученный результат с уравнением связи в общем виде [1,6]. Учитывая, что индекс коэффициента соответствует обобщённой скорости, запишем:

a₁ q ₁ + a ₂ q ₂ + a ₃ q ₃ + a 4 <7 4 + a ₅ <7 5 + a l = 0 .

Из последнего равенства следует:

a ₁ =П ( ф₃ ) • i 1 ; a ₂ =П ( ф₃ ) ; a ₃ =П ( ф₃ ) ; a 4 = 0; a ₅ =-1 .

Определение обобщённых сил проводим, составляя выражение суммы работ на виртуальных перемещениях:

5 A = Md • 5 q ₁ - R ₂ • 5 q ₂ - R ₃ • 5 q ₃ - mg • 5 ( q 4 + q ₅ ) - Frez • 5 ( q 4 + q ₅ ) ;

Q i = Md ; Q 2 =- R 2 ; Q 3 =- R 3 ; Q ₄ =- mg - Frez ; Q 5 =- mg - Frez .

Окончательно систему уравнений вынужденного движения механизма можно записать в матричном виде, выделив пятое уравнение, которое предназначено для определения множителя Лагранжа Л :

	Md + Л a 1		■ Md + ЛП' i1 "
Mq + Hq + Cq =	- R 2 +Л a 2 - R 3 +Л a 3	— =	- R 2 + ЛП ‘ - R 3 +ЛП'
	_- mg - Frez + Л a 4 _		- mg - Frez

mq ₄ + mq ₅ = - mg - Frez - Л.

Последнее уравнение приведённой системы используем для определения множителя Лагранжа:

Л = - mq ₄ - mq ₅ - mg - Frez .

Окончательно систему уравнений привода пилорамы получаем в виде матричного равенства:

( M ■ p ² + H ■ p + C ) -q = F ( X, t ) ;

^{F (}q, t ) =

Md + ЛП' i₁ - R ₂ + ЛП' - R 3 + ЛП' - mg - Frez

Md - П'i1 ■(mq4 + mq5 + mg + Frez) -R2 - П' ■ (mq4 + mq5 + mg + Frez) -R3 - П' ■ (mq4 + mq5 + mg + Frez) -mg - Frez где

m П''

i 1 ■ ( q 4 ⁺ q 5 )

••        •• q4 + q 5

••        •• q4 + q 5

= m П'" Iv ■ q ₄ + m П'" Im ■ q + m П^П"

( ^Iv ■^q ) 2

( ^Iv ■^q ) 2

( ^Iv ■^q ) 2

Iv =

f

;

Im =

10 J

f i i

i ₁

i ₁

1    10

1   10

1   10

0  00

	Md - П' i1 ■ ( mg + Frez )		i 1 ■ ( q 4 + q 5 )		i 1 ■ ( q 4 + q5 )
—	- R 2 - П' ■ ( mg + Frez )	- m П''	• •             • • q 4+ q 5	= F ( t ) - m П'.	• •             • • q 4+ q 5
	- R 3 - П' ■ ( mg + Frez )		••        •• q 4+ q 5	0	• •             • • q 4+ q 5
	_     - mg - Frez     _		.       0       .		.      0      .

Проведём преобразования вектора, определяемого «лишней» координатой: q ₅ = П^ ( Iv ■ q ) ² +П'. Im ■ q;

Матрица инерционных коэффициентов, очевидно, будет иметь вид:

M = M + Iv ■ m ■ П' + Im ■ m ■ П' ■ П'

Тогда система уравнений, описывающая механическую часть привода, может быть пред- ставлена матричным уравнением вида:

Me i + Hq + Cq = F ( t ) - m п'^п"

( ^Iv ■^q ) ²

( ^Iv ■^q ) ²

( ^Iv ■^q ) ²

= Fsum.

Таким образом, нами получено матричное нелинейное дифференциальное уравнение второго порядка относительно выбранных обобщённых координат. Для дальнейшего исследования желательно иметь систему дифференциальных уравнений первого порядка. С этой целью проведём следующие преобразования: матрицы M, H, C рассматриваем как составляющие блочных матриц:

HM

M NulM

NulM

NulM      Fsum

-M ; Q = NulV

Z

Z

где NulM - нулевая матрица 4 x 4; NulV - нулевой вектор 4 x 1 .

Система дифференциальных уравнений первого порядка может быть записана в виде:

R • X + K • X = E • Q, где E - единичная матрица 4 x 4 .

Проводим проверку сделанных преобразований:

NulMI Pq

- m ’ q

Fsum

NulV

H M . q ₊ C M NuIm ] [q] [NulM

В результате получаем:

H • q + q • M + C • q = Fsum;

m • q - m • q = NulM.

Этот результат означает, что нами получена система уравнений, описывающая поведение станка в переменных состояния. Собственная матрица объекта получается в виде:

A = -R-1 • K, матрица управления в виде:

B = R-1 • E, где n'/n    T d8 ■ „ . n          T     sinФ ■ T . n

П ( Ф ) = - L --sin 8 + R • cos ф = L • c---sin 8 + R • cos ф;

d ф                     cos 8

П" ( ф ) = L •

sin 8

cos 8

2 ( sin Ф ]

c 'Ixl

^ V cos 8)

^

-^' cos Ф

)

t x I sin Ф 1

- L cos 8 • I c--|

I cos 8 )

- R • cos Ф.

Заключение. Полученная система уравнений привода в дальнейшем может быть использована для анализа соотношения спектра колебаний, возбуждаемых приводом, как за счёт его динамических свойств, так и за счёт существенной нелинейности закона движения рабочего органа и собственных частот пилы. Кроме того, она может быть использована и при анализе вынужденных движений пилы. Таким образом, поставленная цель настоящей работы реализована, создана математическая модель привода главного движения пилорамы.