Математическая модель процесса функционирования системы "оператор - тренажер"

Моделирование – метод в научном исследовании, позволяющий изучить объект (оригинал) путем создания и исследования его копии (модели) не в натурных условиях, а на модели этого объекта [1, 2].

В нашем случае объектом исследования является процесс функционирования системы управления учебно-тренировочным средством (далее функционирование УТС).

Целью исследования является формальное описание операции в процессе функционирования учебно-тренировочного средства, которое является основой для разработки имитационной модели системы управления УТС [3, 4].

ПОСТАНОВКА ЗАДАЧИ

Управление есть процесс формирования рационального поведения системы при выполнении операции. Процесс подготовки и принятия решения оператором, а также организация их выполнения и контроль активных средств, входящих в периферийное окружение системы управления, составляет сущность описания операции [5, 6].

Анализ существующих средств моделирования и решаемых с его помощью задач показывает, что комплексное решение проблем построения системы управления учебно-тренировочным средством возможно лишь на основе единой формальной математической схемы [7, 8, 9, 10].

МЕТОДЫ И МАТЕРИАЛЫ

Под функционированием УТС следует понимать выполнение обучаемым операции путем воздействия на органы управления и отклика тренажерного средства в виде сигнала отображаемого на контрольно-измерительных приборах с учетом сбора, оценки и передачи информации. В свою очередь функционирование учебно-тренировочного средства является сложным комплексом взаимосвязанных подсистем и устройств, среди которых выделяется три основных подсистемы:

• -    C₁ – подсистема сбора информации и формирования аналогово сигнала управления в результате работы органов управления и контрольно-измерительных приборов;

• -    C₂ – подсистема, в которой учитываются действия обучаемого в модулях рабочего места оператора, условно ее можно назвать оператором, выполняющим тренировочный цикл на учебно-тренировочном средстве;

• -    C₀ – подсистема обработки информации, контроля, оценки и формирование цифрового сигнала управления, за который отвечает модуль управления и контроля.

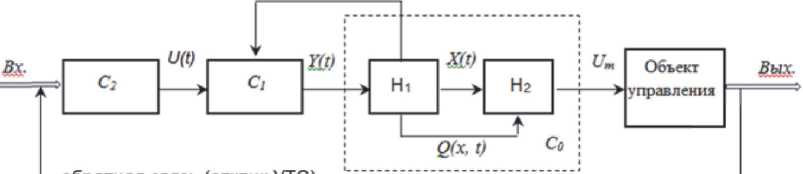
Подсистема C1 включает в свой состав набор датчиков, коммутатор, блок кодирования информации, обеспечивающих формирование вектора аналогово сигнала Y(t) направленного на управляемый объект. Подсистема C0 представляет собой вычислительный комплекс, состоящий из блока H1 и H2, при этом H1 управляет

обратная связь (отклик УТС)

Рис. 1. Функциональная схема основных элементов системы управления

процессом опроса и приема информации о векторе Y(t), на его основе блок H2 оценивает вектор состояния управляемого объекта X(t) и область его допустимых значений Q(x,t). При значениях X(t), принадлежащих Q(x,t), никаких управляющих воздействий на объект не проводится. При неправильных действиях оператора, т.е. в случае когда X(t) не принадлежит Q(x,t), подсистема C0 формирует вектор управления Um, поступающий в виде сообщения об «ошибке». Подсистема C2 служит для формирования воздействия U(t) на объект управления через C1 и C0, в состав которой входят исполнительные механизмы объекта, воспроизводимого в учебно-тренировочном средстве. Обобщенная функциональная схема системы приведена на рисунке 1 [11, 12].

Особенностью рассматриваемого класса учебно-тренировочных средств является то, что тренировочный цикл представляет собой последовательность чередующихся между собой однотипных фаз длительностью (t+1 - t) (рисунок 2). На каждой из фаз можно выделить как минимум два этапа. На первом этапе определяется текущий вектор формирования задания Y(t). При этом в функционировании системы задействованы только две из трех подсистем, а именно С₀, С₁. На втором этапе подсистема С₂ на основе вектора формирования задания Y(t), а в последующем и предыдущем шаге действий, оценивает состояние управляемого объекта X(t), а подсистема С₀ находится в режиме готовности к началу функционирования сигнала U_m (С₀ находится в не-нагруженном состоянии), при достижении X(t) критических значений X _кр с целью блокировки исполнительных органов для предотвращения аварийной ситуации и выдачи соответствующего сообщения об ошибке (С₀ находится в нагруженном состоянии).

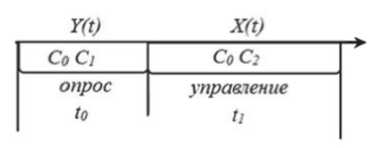
Рис. 2. Тренировочный цикл учебно-тренировочного средства

Отличительной чертой данной системы является то, что подсистема С0 функционирует постоянно, подсистема С1 периодически включается в работу при поступлении управляющих воздействий с подсистемы С2, которая находится в постоянной готовности вступить в работу после принятия соответствующего решения, что напрямую влияет на результат операции и накладывает на нее высокие требования с точки зрения надежности ее функционирования.

Предполагается, что каждая из подсистем удовлетворяет требуемым техническим показателям по надежности и т.п., но обладает собственными показателями точности, качеству, быстродействию на каждом из этапов. В этих условиях актуальной является разработка критерия оценки эффективности функционирования системы, учитывающего выполнение операции как последовательность чередующихся между собой фаз, что позволит проводить сравнительный анализ разных структур построения учебно-тренировочных средств данного класса [13, 14, 15, 16, 17].

В соответствии с произведенным описанием можно установить, что учебно-тренировочное средство, оператор и выполняемая операция представляют собой систему, которая в любой момент времени может находиться в одном из следующих шести различных возможных состояний S:

• S₀    – операция находится в исходном состоянии, поступило задание о виде выполняемой операции, подсистемы C₁, C₂ функционируют в штатном режиме, C₀ находится в ненагружен-ном состоянии;

• S₁    – алгоритм операции выполнен правильно, сообщение об «ошибке» не поступало, подсистемы C₁, C₂ функционирует в штатном режиме, C₀ находится в ненагруженном состоянии;

• S₂    – неправильно выполнен алгоритм, поступило сообщение об «ошибке», подсистемы C₁ функционирует в штатном режиме, C₂ функционирует неправильно, C₀ находится в нагруженном состоянии;

• S₃    – выполнена команда оператором по устранению ошибки, подсистема C₁ функционирует в штатном режиме, C₂, C₀ находится в нагруженном состоянии;

• S₄    – оператор не выполняет никаких действий согласно алгоритму, подсистемы C₁, функционирует в штатном режиме, C₂ не функционирует (сбой работы), C₀ находится в не- нагруженном состоянии;

• S₅    – операция выполнена правильно.

Переход из одного состояния в другое определяется следующими потоками событий и их интервалами:

• в ( t) - неправильное выполнение команды, совершение повторной ошибки;

• 5 ( t) - выполнение команды по устранению ошибки;

• a ( t) - нарушение порядка действий оператора при выполнении алгоритма операции;

• Y ( t) - отсутствие действий оператора по выполнению алгоритма операции;

• т ( t) - правильные действия оператора при выполнении алгоритма операции;

Un(t) Pn(t) – финал выполнения операции (включение оборудования).

Состояние S₅ «финальное». Когда оно достигается, процесс выполнения операции прекращается. Предположим, что процесс выполнения операции произвольно выбранного времени t, такого, что 0 ≤ t ≤ T, параметры, определяющие эффективность выполнения операции и характеризующие нарушение действий оператора или прекращение его активности постоянны. Тогда возможные переходы системы из состояния в состояние в соответствующие им вероятности перехода за малый промежуток времени At могут быть описаны в таблице и блок-схемой состояний на рисунке 3.

Т – максимальное время, отводимое на выполнение операции (тренировки).

Если рассмотреть состояние S0, то можно отметить вероятность того, что операция будет выполнена, а возобновление активности оператора на каждом шаге тренировки не зависит от того, что было перед ним: S2, S3, S4, т.е. отсутствует накопление информации о предыдущем шаге алгоритма в рамках выполнения одной операции, в связи с разными типами выполняемых действий обучаемыми, при условии что оператор выполняет норматив впервые.

Значит, вероятность событий выполнения операции не зависит от того, в каком состоянии находилось учебно-тренировочное средство до начала (S2, S3, S4).

Таким образом, для каждого момента времени t0 вероятность любого состояния системы в будущем (при t > t0) можно считать зависит только от его состояния в настоящем (при t = t0) и не зависит от того, когда и каким образом система пришла в это состояние (т.е. как развивался процесс во времени). Значит, процесс выполнения операции в учебно-тренировочном средстве можно представить, как неоднородный Марковский случайный процесс.

Обозначим P^t) - вероятность того, что в момент времени t процесс выполнения операции будет находиться в состоянии S₁, S₂ … S₅, несовместимы и образуют полную группу. Зная взаимосвязь состояний (таблица 1 и рисунок 3), можно описать систему уравнений Колмогорова [18, 19], описывающую по времени изменение вероятностей P i (t) :

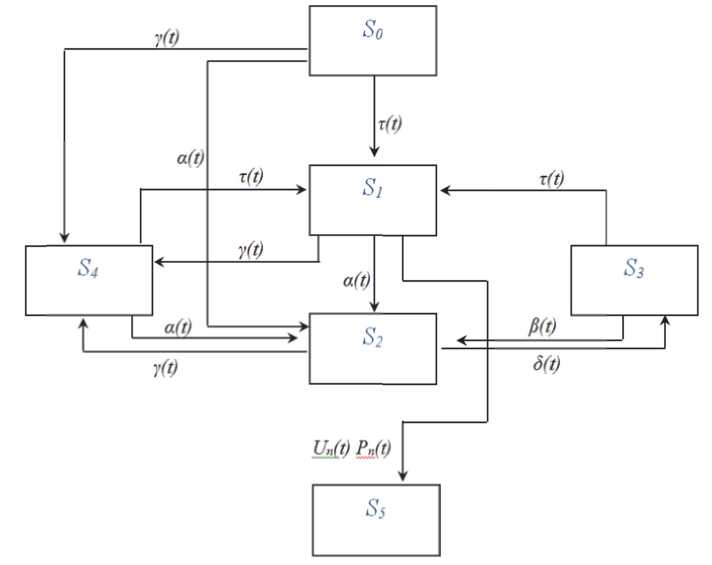
Рис. 3. Блок-схема состояний процесса выполнения операции

Таблица 1. Структура возможных переходов за время ∆ t и соответствующие значения вероятностей P _i (t)

Состояние к моменту времени t		Возможные переходы в другие состояния за время At
Обозна чение	Характеристика состояний	Обозна чение	Характеристика происходящего события	Вероятно сть перехода
S 0	операция находится в исходном состоянии, поступило задание о виде выполняемой операции, подсистемы C i , C 2 функционируют в штатном режиме, C o находится в ненагруженном состоянии;	S 1	оператор выполняет правильные действия	1(0
		S 2	оператор выполняет не правильные действия, совершена ошибка	a (t)
		S 4	оператор не воздействует на объект в течение времени ( Т ожидания )	y(t)
S 1	алгоритм операции выполнен правильно, сообщение об «ошибке» не поступало, подсистемы C i , C 2 функционирует в штатном режиме, C o находится в ненагруженном стоянии;	S 5	Операция выполнена правильно (включение оборудования)	V „ (t) P n (t)
		S 2	оператор выполняет не правильные действия, совершена ошибка	a(t)
		S 4	оператор не воздействует на объект	y(t)
S 2	не правильно выполнен алгоритм, поступило сообщение об «ошибке», подсистемы C i функционирует в штатном режиме, C 2 функционирует неправильно, C o находится в нагруженном состоянии;	S 3	выполнение команды по устранению ошибки	5(t)
		S 4	оператор не воздействует на объект	y(t)
S 3	выполнена команда оператором по устранению ошибки, подсистема C i , функционирует в штатном режиме, C 2 , C o находится в нагруженном состоянии;	S 1	оператор выполняет правильные действия	T (t)
		S 2	оператор выполняет не правильные действия, совершена повторная ошибка	P(t)
S 4	оператор не выполняет ни каких действий согласно алгоритма, подсистемы C i , функционирует в штатном режиме, C 2 не функционирует (сбой работы), C o находится в не нагруженном состоянии.	S 1	оператор выполняет правильные действия	T(t)
		S 2	оператор выполняет не правильные действия, совершена ошибка	a (t)

В качестве математической модели объекта рассмотрим систему дифференциальных уравнений:

^52 = _[T(t)+a(t)+Y(t)]. p0(t). dt

^^p 5 7^t) = HaW + vCt) + « п (ЖГО^] . P₁⁽t⁾ + т(У • [Р о (У + P₃(t) + P₄(t⁾];

= _[6(t) + _Y(t)] • P₂(t) + P(t) • P₃(t) + a(t) • [P o (t) + P i (t) + P 4 (t)]; dt

5^ = _[P(t) + T(t)] • P3(t) + S(t) • P2(t).

dt dP.(t)

-dp = _[T(t) + a(t)J • R , (t) + Y(t) • [P o (t) + P i (t) + P 2 (t)];

^dPd^(t) = » n (t)P n (t) • P i (t).

Система представляет собой систему линейных уравнений с переменными коэффициентами. Вследствие значительного числа уравнений и сложной связи между ними решение этой системы в аналитическом виде является громоздким, поэтому такую систему необходимо решать численно. С использованием ЭВМ решение ее особых трудностей не представляет.

ЗАКЛЮЧЕНИЕ

Описанная математическая модель процесса функционирования системы «оператор – тренажер» легла в основу разработки имитационной модели, с целью последующей верификации разработанной модели системы управления с ее оригиналом, а также прогнозирования поведения системы путем снятия показателей ее характеристик при моделировании [20, 21, 22].