Математическая модель процесса гомогенизации молочных продуктов высокой жирности на основе цепи Маркова

Для замедления процессов отстаивания жира во время хранения молока и жидких молочных продуктов используются процессы гомогенизации. Под степенью гомогенизации обычно понимают средний размер жировых шариков, степень устойчивой во времени однородности (гомогенности) в смысле отсутствия микроконцентрационных неоднородностей, образующихся при смешивании взаимно-нерастворимых веществ [1]. Однако для более глубокого исследования дисперсности жировой фазы помимо интегральных характеристик используются распределения жировых шариков по их размерам, расстояния между шариками, площади поверхности и т. д. [2]. Особую актуальность исследования распределений жировых шариков по их размерам (массе) приобретают при анализе жидких молочных продуктов высокой жирности, в частности сливок. Так, размер жировых шариков в сливках оказывает существенное влияние на процесс мас-лообразования и степень использования жира [1]. При разработке нового технологического оборудования, а также режимов его работы возникает необходимость математического моделирования изменения функции распределения жировых шариков по размерам(массе) с изменением какого-либо технологического параметра [3].

В работах [4] предлагается подход к построению математической модели процесса гомогенизации молока как случайного процесса на основе аппарата цепей Маркова с дискретными состояниями и непрерывным параметром, за который принято давление гомогенизации. В основу модели положены следующие предположения. Под действием внешних факторов система может переходить из одного состояния в другое. Система принимает состояния, которые ассоциированы с количеством жировых шариков определенной массовой или объемной фракции. Множество состояний X = { x 1 ,x 2 ,...,Xj ,..., x_N } , i = 1, N, где x – числовой диапазон количества жировых шариков в i -ой фракции. При синтезе структуры модели, приняты следующие допущения: процесс гомогенизации носит последовательный характер; интенсивность перехода из одного состояния в другое отражает интенсивность процесса гомогенизации и характеризуется величиной λ i,j , а скорость изменения вероятности обратного перехода равна нулю; процесс гомогенизации моделируется переходом из состояния X I в x j , где j >i , при этом интенсивностью переходов λ j,i пренебрегаем; состояние системы характеризуется вероятностью P i , где t = 1, N , где N - количество фракций [4]. При принятых допущениях граф для шести состояний представлен на рисунке 1.

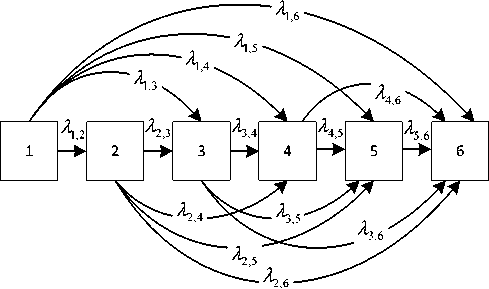
Рисунок 1. Граф состояний без учета обратных переходов

Figure 1. State graph without taking into account the reverse transitions

Однако по данным исследований, проводимых в ряде работ [2, 3], при увеличении жирности гомогенизируемого продукта возникают обратные гомогенизации эффекты коалесценции. В этом случае предлагаемая в [4] математическая модель процесса гомогенизации не будет учитывать обратные процессы слипания жировых шариков и не может применяться для описания гомогенизации молочных продуктов высокой жирности (например, сливок).При обработке экспериментальных данных по методике [5], построении соответствующих массовых распределений жировых шариков и использовании математической модели без учета процессов слипания жировых шариков, будет наблюдаться стремление к нулю интенсивностей переходов из фракций с высокой массой шариков во фракции с более низкой массой, начиная с некоторого значения давления и массы жировых шариков в объёме пробы. Это объясняется тем, что оцениваемая по модели без учета обратных переходов «кажущаяся» интенсивность перехода будет являться разницей интенсивностей прямого и обратного переходов. В ряде проведенных вычислительных экспериментов интенсивности прямых переходов принимали отрицательные значения, что обусловлено большей интенсивностью процессов слипания жировых шариков.

Теоретическая часть

Для учета возникающих в ходе гомогенизации механизмов коалесценции предлагается модифицировать предложенную в [4] модель учетом дополнительных переходов из фракций с меньшим размером жировых шариков во фракции с большим размером. Для этого необходимо ввести в математическую модель интенсивности обратных переходов, которые характеризуются величиной H j ,_t . Соответствующий граф переходов для шести состояний и эффектом коалесценции, начиная с четвертого состояния, представлен на рисунке 2.

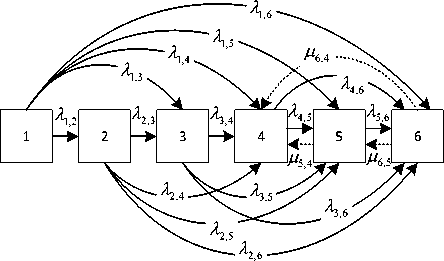
Рисунок 2. Граф состояний с учетом обратных переходов Figure 2. State graph with taking into account the reverse transitions

В общем случае для N состояний система дифференциальных уравнений, описывающая вероятности Pn нахождения в каждом из состояний n    (эквивалент количества жировых шариков во фракции) для графа состояний, представленного на рисунке 2, запишется как (2). В этой системе индекс M соответствует фракции, начиная с которой проявляются эффекты слипания жировых шариков. Начальные условия дифференциальных уравнений соответствуют массовому распределению жировых шариков негомогенизированного молочного продукта. На значения интенсивностей переходов накладываются ограничения, они не могут принимать отрицательные значения.

“P ( P )     /                                  x .

• "     =- ( ^A 1,2 ^{+ A} 1,3 ⁺ ... ^{+ A} 1, n ⁺ ... ^{+ A} 1, N ) ^P1 ⁽ p ) ;

dp

“    ' = A, P (P)- dp

• - ^{( A} 2,3 ^{+ A} 2,4 ⁺ ... ^{+ A} 2, n ⁺ ... ^{+ A} 2, N ) ^P2 ^{( P ) ;}

Задаваясь матрицами интенсивностей прямых переходов λ cэлементами

	"-]E A k k = 2	0        ..	.0.	..   0
	A ,2	N - Z A 2,k  . k = 3	.0.	..   0
[ A > ] =	A 1,n	.. A 2,n       .	. N .   - Z A2,k   . k = n	..   0

A 1,m         A 2,_m     ...    - ^ A ^i _t   ...  0

l = m

,N            2,N       ...        n,N обратных переходов ци вектором вероятностей состояний P с элементами

0   0   ...      0      ...0

0   0   ...      0      ...0

.    0   0   ...      0

. A, J =

M m + 1, m   ... M n , m

0  0  ...     00

P 1

P 2

dP ( P )

= A , P ( P ) + ^P ( p ) + ... + dp

+A , P . (p)- n-1 ,n n-1

• -    A „ + A „ + ... + A _M }P(p) ; n , n + 1         n , n + 2                n,N n

“Py^ = A P ( p ) + A 2N P 2 ( p ) + ... + dp

^+A n , N^Pn ^{( p} ) ⁺ ... ^{+ A} N - 1, N^PN - 1 ^{( p} ) -

• - ^{( M} N , M ^{+ P} N , M + 1 ⁺ ... ^{+ P} N , N - 1 ) ^PN ^{( p} ) ;

P 1 ( 0 ) = P. 0 ,P 2 ( o ) = P 20 ,...,P ( 0 ) = P no ,...,

• ^p n ( 0 ) = ^PN o ;

j 0, м„ > 0, i = 1, N , j = 1, N .

[ P ] =

L Pn J в матричном виде система запишется в виде dP = X ■ P - И ■ P , P p=0 = P0.       (2)

dp

Экспериментальная часть

В качестве экспериментальных данных использовались результаты, представленные в [2]. Цельное молоко 3,5% жирности гомогенизировалось на лабораторном гомогенизаторе фирмы APV в интервале изменения давления от 0 до 500 атмосфер через каждые 100 атмосфер. Температура гомогенизации 60 °С.

После гомогенизации молоко охлаждалось до 20 °С, после чего по известным методикам подготавливались образцы для оценки дисперсности жировых шариков с использованием микрофотографий [2]. Результаты исследований представлены на рисунке 3. Далее данные были нормированы для каждого значения давления гомогенизации из условия

N

2 р ( a)=i,              (2)

= 1

где N – число фракций.

Для этого были введены дополнительно коэффициенты нормировки, на которые умножаются исходные значения долей фракции для каждого распределения, полученного при заданном j-м давлении гомогенизации, что обеспечило выполнение равенства (3).

^kKO_P» , j = N        , ^j = ¹ J ,        ⁽³⁾

2 P ( P i )

= 1

где J – количество экспериментальных точек, соответствующих давлениям гомогенизации.

Результаты обработки и нормировки данных экспериментов представлены в таблице 1. Для дальнейших исследований для исходного образца цельного молока было принято значение давления гомогенизации, равное нулю.

Таблица 1.

Экспериментальные данные после нормировки

Table 1.

Experimental data after normalization

Давление, атм Pressure, atm	Р1	Р2	Р3	Р4	Р5	Р6
0	0,172	0,186	0,27	0,26	0,09	0,018
100	0	0,005	0,01	0,482	0,43	0,07
200	0	0,0039	0,009	0,145	0,57	0,27
300	0	0,0033	0,009	0,027	0,58	0,38
400	0	0	0	0,047	0,53	0,421
500	0	0	0	0	0,51	0,489

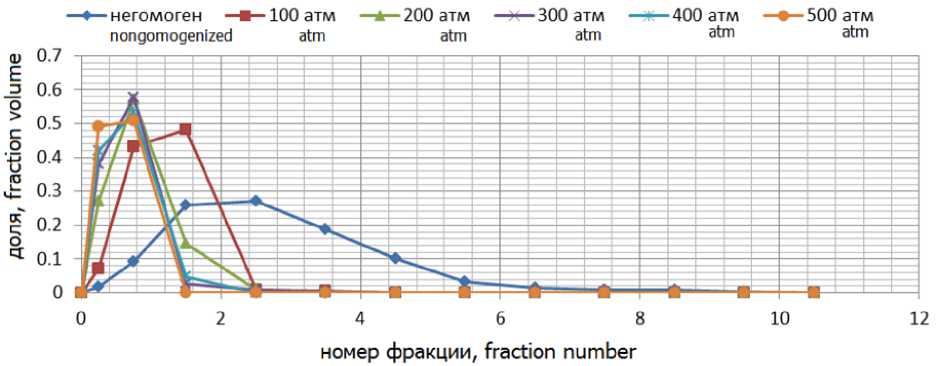
Рисунок 3. Массовые распределения жировых шариков в объеме пробы

Figure 3. Mass distribution of fat globules in probe

Математическое моделирование

Математическая модель процесса гомогенизации для случая 6-ти фракций описывается системой (5). При этом считается, что процесс слипания жировых шариков начинается с четвертой фракции. Выбор номера фракции, начиная с которой необходимо учитывать процесс слипания жировых шариков, можно осуществлять как из визуального анализа графиков экспериментальных данных, так и при анализе результатов параметрической идентификации математической модели процесса гомогенизации без учета обратных переходов. Так, при оценке параметров модели (5) с интенсивностями переходов Hj,i, равными нулю, и при снятии ограничений ^i,j - 0, были получены отрицательные интенсивности, начиная с четвертой фракции.

dP i ⁽ p ) _ у ■>

IT -§ AP (p);

Pp1 = A. P, (p )-£ A,P (p);

dpi dp'=E A , P (p )-£ AP (p);

dp       i=1

dP^1=£ a, P (p )-£ v, (p)+ dp       i=1

^<+ ^ 5,4 ^P 5 ( p ) ⁺ ^ 6,4 ^P 6 ( p ) ;

dP T p ) = E ^A ,5 ^P ( p ) ^{- A} 5,6 ^P 5 ( p ) ^{+ p} 6,5 ^P 6 ( p ) ;

dp d^ = E A» P (p)-P65 P (p);

dp

P , ( 0 ) = P_V 0 ,P 2 ( 0 ) = P .0 , P , ( 0 ) = P ,,0 ,

P , ( 0 ) = P ,,0 , P 5 ( 0 ) = P 5,0 , P 6 ( 0 ) = P 60 ;

A> 0, ц^> 0.(4)

Математическая модель реализована в интерактивной графической среде MathWorks Simulink™ [7].

Для численного поиска значений параметров минимизировалось среднеквадратичное отклонение расчетных данных от экспериментальных по каждой фракции:

• ⁵    = EE]E ( P_y .( p? ) эксп - P j ( p,) расч ) 2 -^ min ,⁽⁵⁾ j = 1 , = i

где M, N – количество фракций и точек контроля при заданном давлении гомогенизации соответственно.