Математическая модель процесса нейтрального выщелачивания и сгущения в производстве цинка

Выщелачивание продуктов обжига – основной технологический передел производства цинка гидрометаллургическим способом, который в значительной мере определяет технико-экономические показатели производства в целом, в первую очередь извлечение металла, расход электроэнергии, себестоимость цинка [1].

Цель процесса выщелачивания – более полное извлечение цинка и других полезных компонентов сырья в раствор при минимальном его загрязнении примесями.

Исходным сырьем является огарок, получаемый в результате окислительного обжига цинкового сульфидного материала. Выщелачивание представляет собой процесс растворения цинкового огарка в жидком растворителе. На практике процесс осуществляют отработанным электролитом, получаемым в процессе электролиза раствора сульфата цинка. При выщелачивании в раствор переходят цинк, кадмий, медь, железо и другие компоненты. Нерастворимые в слабых растворах серной кислоты соединения остаются в твердом остатке от выщелачивания – кеке.

При непрерывном способе производства цинка выщелачивание включает две ступени. Задача первой стадии выщелачивания – получение раствора, пригодного для очистки растворов от примесей железа, алюминия, мышьяка, сурьмы, крем-некислоты методом гидролиза, что можно провести лишь в нейтральной среде (рН = 5,2–5,4).

Цинк содержится в огарке в виде соединений: ZnO, ZnSO4, ZnS, ZnO·Fe2O3, 2ZnO·SiO2. Оксид цинка растворяется в растворе серной кислоты. Сульфат цинка хорошо растворяется в воде, поэтому цинк, содержащийся в сульфатной форме, полностью переходит в раствор на нейтральной стадии выщелачивания. Феррит и сульфид цинка в разбавленных растворах серной кислоты практически нерастворимы и переходят в твердый остаток. Наиболее легко растворяется оксид меди с образованием сульфата меди. Ферриты и сульфиды меди переходят в кек. Кадмий присутствует в обожженном концентрате в виде СdО, CdSO4, CdS, СdO·Fe2O3. Хорошо растворяется оксид кадмия с образованием сульфата. Ферриты и сульфиды кадмия переходят в твердый остаток. Свинец при сернокислотном выщелачивании практически весь переходит в кек в виде труднорастворимого сульфата PbSO4. Присутствующий в огарке оксид железа FeO легко взаимодействует со слабой серной кислотой; трехвалентное соединение Fe2O3 практически не растворимо. При выщелачивании обожженного концентрата получается нейтральная пульпа (смесь сульфатного раствора и нерастворимого остатка) с содержанием твердого 20–70 г/л. Для проведения последующих технологических операций ее подвергают разделению на твердую и жидкую фазы путем сгущения и отстаивания. Здесь протекают довольно сложные физикохимические процессы, которые внешне проявляются в осаждении твердых частиц в жидкой среде. После отстаивания получается верхний слив с содержанием твердого 1– 4 г/л и сгущенная пульпа с определенным отношением масс жидкой и твердой фаз (ж :т) = (2–3) : 1.

Рассматривая процессы нейтрального выщелачивания и сгущения как единый объект, выделим основные группы его параметров. Входными параметрами являются расход потока огарка, верхнего слива кислых сгустителей (ВСКС) и поток отработанного электролита (ОЭ). Продукты передела – верхний слив нейтральных сгустителей (ВСНС), нижний слив нейтральных сгустителей (НСНС), содержащий твердую фазу НСНС т и жидкую фазу НСНС_ж.

С целью исследования процесса нейтрального выщелачивания цинковых огарков и изучения его характеристик интерес представляет получение математической модели, позволяющей определять количество получаемых продуктов рассматриваемого производственного передела на основе информации о количестве поступающих на переработку материальных потоков и их химических составах.

Математическую модель выщелачивания и сгущения представим в виде совокупности балансовых соотношений по твердой и жидкой фазам, а также по компонентам, переходящим в раствор и образующим «цинковый» кек.

Баланс по твердой фазе определяется соотношением:

^F НСНС_т = F 1 ⁽ C ZnO ⁽¹ - ^a 1 ) + C 2ZnOSiO₂⁽¹ -^a 1 ) +

+ C ZnS + C ZnO . Fe 2 O 3 + C CuS + C CuS . Fe₂O₃ + C PbO +

+ C PbSO₄ + C CdS + C CdO . Fe₂O₃ + C SiO₂ +

+ C ^3 + C Пр ),                         (1)

где FНСНС – расход твердой фазы нижнего слива нейтральных сгустителей, кг/ч; F1 – расход огарка, кг/ч; C1ZnO – содержание в огарке оксида цинка, %; C2ZnO.siO2 — содержание силиката цинка в огарке, %; C1ZnS – содержание в огарке сульфида цинка, %; CZnO.Fe2O3 — содержание в огарке феррита цинка, %; CC1 uS – содержание в огарке сульфида меди, %; СcuO.Fe2O3 — содержание феррита меди в огарке, %; C1PbO – содержание оксида свинца в огарке, %; CP1bSO – содержание сульфата свинца в огарке, %; C1Fe O – содержание в огарке оксида железа (III), %; Cп1р – содержание прочих компонентов в огарке, %; α1 – доля оксида цинка, пере- шедшего в раствор.

Баланс по жидкой фазе:

^Q ВСНС ^р ВСНС = Q ВСКС ^р ВСКС ⁺ F 1 ^{+ Q} O3 ^р O3 -

FНСНСт бнСНСж рНСНСж,

6нСНС„ рНСНС„ = FНСНСT а2, жжт где QВСНС — расход ВСНС, м3/ч; рВСНС - плотность ВСНС, кг/м3; QВСКС – расход ВСКС, м3/ч; рВСКС — плотность ВСКС, кг/м3; F1 - расход цинкового огарка, кг/ч; QО3 - расход ОЭ, м3/ч; рО3 -плотность ОЭ, кг/м3; Q – расход жидкой ж фазы НСНС, м3/ч; рнснс - плотность жидкой ж фазы НСНС, кг/м3; а2 - величина ж: т в НСНС.

Балансовое соотношения по цинку в растворах:

ВСНС         ВСКС

⁽ Q ВСНС ⁺ Q НСНС™ ) С Zn    = Q ВСКС С Zn    ⁺

ж

⁺ Q O3 С Zn^{3 + [а} 1 ^F 1 ⁽ C ZnO ^z1 ⁺ C 2ZnO . SiO₂ ^z 2 ) ⁺

^{+ F} 1 C ZnSO₄ ^z 3 ] ,                                ⁽⁴⁾

где С _Z ^В _n ^СНС – концентрация цинка в ВСНС, г/л;

ВСКС                                   ОЭ

С _Zn – концентрация цинка в ВСКС, г/л; С _Zn – концентрация цинка в ОЭ, г/л; z ₁ , z ₂ , z ₃ – стехиометрические коэффициенты пересчета; C ¹ _ZnSO – концентрация сульфата цинка в огарке, %.

Балансовое соотношение по меди в растворе:

ВСНС         ВСКС

^{( Q} ВСНС ^{+ Q} НСНС„ ) ^С Си    = ^Q ВСКС С Cu    ⁺

ж

+ F 1 ( C CuO z 4 + C CuSO₄ z 5 ) ] ,                    (5)

где С _C ^В _u ^СНС – концентрация меди в ВСНС, г/л; С _C ^В _u ^СКС – концентрация меди в ВСКС, г/л; z ₄ , z ₅ – стехиометрические коэффициенты пересчета; C ¹ _CuSO – концентрация сульфата меди в огарке, %;

C ¹ _CuO – концентрация оксида меди в огарке, %.

Балансовое соотношение по кадмию в растворе:

^{( Q}В СНС ^{+ Q} НСНС Ж ) ^ССВСНС

ВСКС

= ^Q ВСКС С Cd

+

^{+ F} 1 C CdO z 6 ⁺ C CdSO₄ z 7 , ⁽⁶⁾ где С _C ^В _d ^СНС – концентрация кадмия в ВСНС, г/л; С _C ^В _d ^СКС – концентрация кадмия в ВСКС, г/л;

z ₆ , z ₇ – стехиометрические коэффициенты пересчета; C _C ¹ _dSO – концентрация сульфата кадмия в огарке, %; C ¹ _CdO – содержание оксида кадмия в огарке, %.

Баланс по компонентам, образующим твердую фазу НСНС:

F НСНСт	НСНСт С ZnO    =	(1 — « 1 ) F 1 C ZnO ,	(7)
F НСНСт	НСНСт С 2ZnO . SiO 2	= (1 - а 1 ) F1 C 2ZnO . SiO 2 ,	(8)
F НСНСт	НСНСт С ZnS    =	F 1 C Z 1 nS ,	(9)
F НСНСт	С НСНСт ZnO . Fe 2 O 3	= F 1 C ZnO . Fe2O3 ,	(10)
F НСНСт	НСНСт С CuS    =	F 1 C C1uS ,	(11)
F НСНСт	НСНСт С CuO . Fe 2 O 3	= F1 C CuO . Fe2O3 ,	(12)
F НСНСт	НСНСт С PbSO 4 =	F 1 ( C PbSO4 + C PbO z 8 ) ,	(13)
F НСНСт	НСНСт С CdS    =	F 1 C C1dS ,	(14)
F НСНСт	НСНСт С CdO . Fe 2 O 3	= F1 C CdOTe2O3 ,	(15)
F НСНСт	НСНСт С SiO 2    =	F 1 C S 1 iO2 ,	(16)
F НСНСт	НСНСт С Fe 2 O 3   =	F 1 C F1e2O3 ,	(17)
F НСНСт	НСНСт С пр     =	F 1 C п1р ,	(18)

НСНС где СZnO т – содержание оксида цинка в твердой фазе НСНС, %; СНСНСт – содержание силиката 2ZnO.SiO2

цинка в твердой фазе НСНС, %; С _Z ^Н _n ^С _S ^НСт – содержание сульфида цинка в твердой фазе НСНС, %;

НСНС

СZпO.FeT2Oз - содержание феррита цинка в твердой фазе НСНС, %; СPНbСSНOСт – содержание сульфата свинца в твердой фазе НСНС, %; СCНdСSНСт – содержание сульфида кадмия в твердой фазе НСНС, %; СCНdСOНFСeт O – содержание феррита кадмия в твер- дой фазе НСНС, %; СSНiOСНСт – содержание кремнезема в твердой фазе НСНС, %; СFНeСOНСт – содержание оксида железа (III) в твердой фазе НСНС, %; НСНС

С _пр  ^т – содержание прочих компонентов в твер-

С CuO ^z 4 + С CuSO₄ ^z 5 ,

Q BCHC + Q HCHC ж

b 15 =

ВСКС С Cd

Q BCHC + ^Q HCHC„

ж

дой фазе НСНС, %; z ₈ – стехиометрический коэффициент пересчета.

Система соотношений (1) – (18) представляет математическую модель нейтрального выщелачивания и сгущения нейтральных пульп. Особенности модели позволяют перейти к ее топологическому аналогу. На рис. 1 представлен сигнальный граф объекта, отражающий причинно-следственные связи между переменными (сигналами). Вершины сигнального графа соответствуют переменным модели, а ветви – коэффициентам или передаточным функциям, характеризующим связь между переменными.

Коэффициентам передач графа соответствуют соотношения:

^b1 = C ZnO ^a 1 + C 2ZnOSiO 2 ^a 1 + C ZnS + С ZnO - Fe₂O₃ +

С CdO ^z 6 + С CdSO₄ ^z 7 b 16 =-------------⁴— ;

Q BCHC + Q HCHC. ж

+ C CuS + C CuS - Fe₂O₃ + C PbO + C PbSO₄ + C CdS +

+ C CdO - Fe₂O₃ + C SiO₂ + C Fe₂O₃ + C 1р ;

b 2     ^a 2   ; b 3 = Р ВСКС ; b 4 = ——

Piiciic,          Р вснс         Р вснс

ж

b 5 = _Р оЭ_ ; b 6 =--—; b 7 = - ^{Р нСНС} ж ;

Р вснс         Р вснс         Р вснс

ВСКС                  ОЭ b 8 =----С”-------; b 9 =-----CZn------

QВСНС + QНСНС       QВСНС + QHCHC„ жж

b 10 =

^a 1 C ZnO ^z1

b 12 =

Q BCHC + ^Q HCHC„ ж

C ¹ZnSO₄ z 3

^a 1 C 2ZnOSiO₂ ^z 2 b 11 =---------------- ²-----;

Q BCHC + Q HCHC.,. ж

b 13 =

ВСКС С _Cu

_{b 17} = ^{(1- a} 1 ) С ZnO . _{b 18} = ^{(1 a} 1 ) С 2ZnOSiO 2 .

F НСНС_т              F НСНС_т

• b 19 = ⁽ Zn^S ; b 20 = ^ZnO ' ^Fe2O 3 ;

F НСНС_т          F НСНС_т

1¹ b 21 = -^C Cu^ ; b 22 = h CuOIeA ;

F НСНС_т          F НСНС_т

С PbO + С PbSO₄ ^z 8

• b 23 =-----------⁴— ;

F НСНС_т

F НСНС_т          F НСНС_т

11   1

• b 26 =    ^SiO 2 ; b 27 = ^Fe 2 ^O3 ; b 28 =--- пр— .

F НСНС_т         F НСНС_т         F НСНС_т

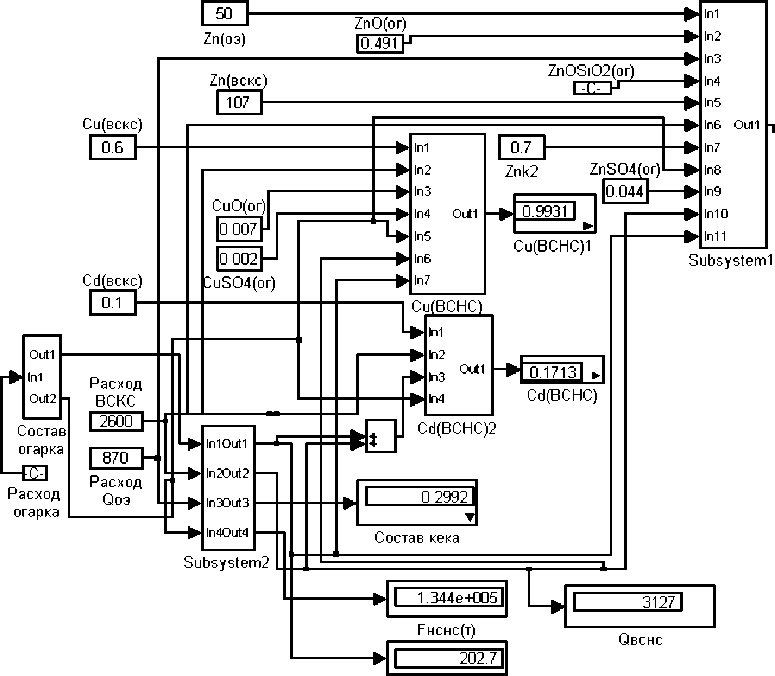
Решение сигнального графа может быть найдено с помощью операций эквивалентного последовательного преобразования [2]. Топологическая модель объекта была реализована в приложении Simulink вычислительной среды MATLAB (рис. 2).

При проведении вычислительного эксперимента полагалось, что в выщелачивательный цех подается обожженный цинковый концентрат в количестве 3,79 т/ч следующего состава, %: ZnO – 49,079; ZnSO 4 – 13,29; 2ZnO·SiO 2 – 4,42; ZnS – 0,76; ZnO·Fe 2 O 3 – 19,56; CuO – 0,69; CuSO 4 – 0,20; CuS – 0,119; CuO·Fe 2 O 3 – 0,30; CdO – 0,125; CdSO 4 – 0,034; CdS – 0,035; CdO·Fe 2 O 3 – 0,07;

Q BCHC + Q HCHC,,

ж

Q BCHC + Q HCHC ж

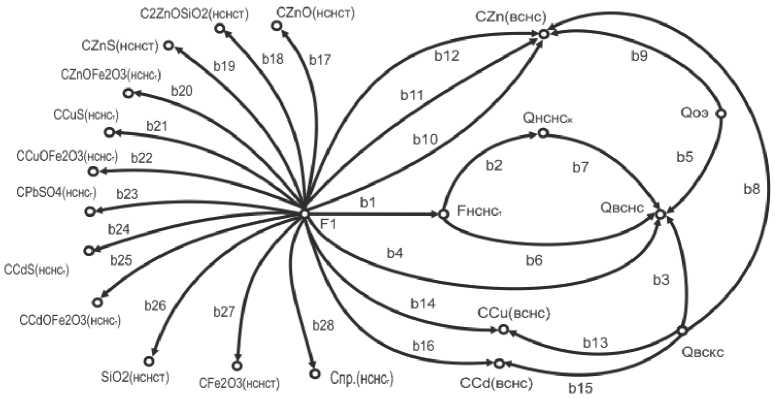
Рис. 1. Сигнальный граф процесса нейтрального выщелачивания и сгущения

Онснс(ж)

Рис. 2. Simulink-модель процесса нейтрального выщелачивания и сгущения

Zn(BCHC)

PbSO 4 – 1,14; PbO – 0,85; FeO – 0,87; Fe 2 O 3 – 0,568; SiO 2 – 1,97; прочие – 5,99.

Для взаимодействия с огарком поступает ВСКС в количестве 118 м³/ч, содержащий: Zn – 107 г/л; Cu – 0,6 г/л; Cd – 0,1 г/л; H 2 SO 4 – 1,5 г/л и отработанный электролит в количестве 36 м³/ч, содержащий: Zn – 50 г/л; H 2 SO 4 – 0,1 г/л. Значения α 1 , α 2 и плотности соответствующих веществ являются исходными данными для расчета, полученными по данным практики работы цинкового производства.

В результате расчета получено: расход ВСНС – 141,6 м3/ч; расход НСНСж – 2,74 м3/ч; расход

НСНС_т – 1822 кг/ч. ВСНС содержит: Zn – 108 г/л; Cu – 0,7 г/л; Cd –0,1 г/л. Состав НСНС т , %: ZnO – 29,92; 2ZnO·SiO 2 – 2,82; ZnS – 1,4; ZnO·Fe 2 O 3 – 39,61; CuS – 0,603; CuO·Fe 2 O 3 – 0,203; CdS – 1,016; CdO·Fe 2 O 3 – 2,031; PbSO 4 – 1,62; Fe 2 O 3 – 1,625; SiO 2 – 1,016, прочие – 14,22.

Полученная математическая модель позволяет получить статические характеристики объекта моделирования в виде зависимостей Q _ВСНС( Q _ВСКС), C Zn(ВСНС) ( Q ВСКС ), Q ВСНС ( Q ОЭ ), C Zn(ВСНС) ( Q ОЭ ) (рис. 3–6).

Таким образом, разработанное математическое описание процесса нейтрального выщелачи-

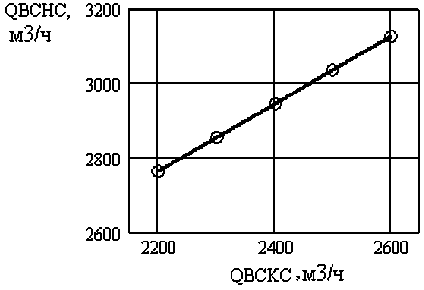
Рис. 3. Статическая характеристика Q ВСНС ( Q ВСКС )

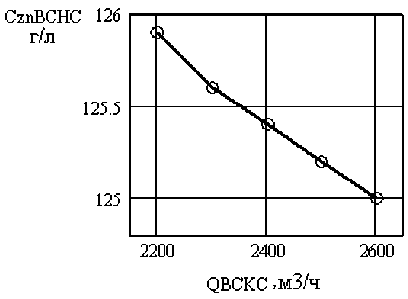
Рис. 4. Статическая характеристика C Zn(ВСНС) ( Q ВСКС )

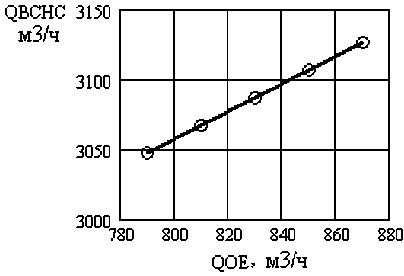
Рис. 5. Статическая характеристика Q ВСНС ( Q ВСКС )

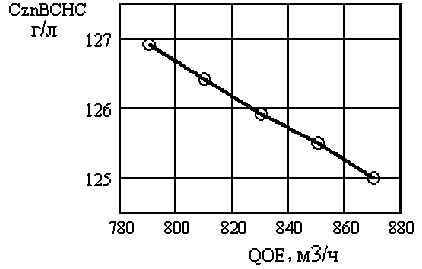
Рис. 6. Статическая характеристика C Zn(ВСНС) ( Q ВСКС )

вания и сгущения позволяет прогнозировать количественные значения массовых расходов выходных материальных потоков ВСНС, НСНСт, НСНСж, а также их компонентов на основе измерительной информации о массовых расходах входных потоков. Математическая модель может быть использована при проектировании новых и анализе функционирования действующих гидрометаллургических систем, а также для решения вопросов по установлению расходных норм по сырью, технологическим показателям и определе- нию неучтенных потерь компонентов сырья в условиях промышленной эксплуатации.