Математическая модель процесса охлаждения стальных заготовок

Рис. 1. Расчётная схема процесса охлаждения:

1 – заготовка; 2 – охлаждающая среда; 3 – форсунка спрейера; А, В, C – расчётные точки на границах и в середине заготовки

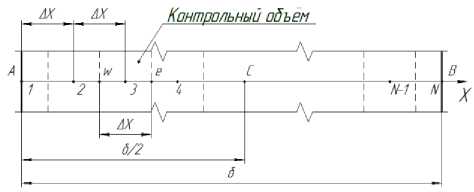
Рис. 2. Расчётная схема заготовки:

1, 2, 3, 4 ... N-1, N – номера контрольных объёмов; w, e – границы 3-его контрольного объёма; Δ Х – шаг между центрами контрольных объёмов

Математическая модель процесса охлаждения. Распределение температуры в теле описывается дифференциальным уравнением теплопроводности Био-Фурье:

S

— ( cpT ) = div ( Л • gradT ) + Q w

• ^d t                                   ,       (1)

Здесь Q w - мощность внутренних источников тепловыделения; теплофизические характеристики материала заготовки: c - теплоёмкость , р -плотность, X - теплопроводность.

При решении уравнения (1) пренебрегает-ся выделением и поглощением теплоты при фазовых переходах в материале (отсутствуют внутренние источники тепловыделения), рассматривается одномерная задача теплопроводности. С учётом допущений уравнение (1) примет вид:

®(срт )=А[ л dT ]

d t        дx V   Sx )

,

Начальное условие: T(x,t)=T0 при t=0. Граничные условия для обратной задачи теплопроводности: T(x,t)=T0(t), при x=0 и x=5. Для прямой задачи теплопроводности: а

^{( т}А ^- T A ) ^Л     при x =0

и а T - T* )= -Л ^Х при x=5 TA и TB - темпе ратуры на поверхности в точках А и В. В дальнейшем TA и TB и будут записываться как T.

Коэффициент теплоотдачи а ₂ рассчитывается как сумма: а ₂ = а + а - конвективного коэффициента а и коэффициента теплоотдачи излучением ^а , который, определяется так [2, с. 194]:

, = а^ ⁴ -^{( т} ' У 1 ( T - т *)

,

« св = у • С • ( Gr • Pr ) ^-

,

где C и n - коэффициенты (С=1,18, n=0,125, при 10^-32; C=0,54,n=0,25 при 5 10²7; C=0,135, n=0,33 при 2 10⁷13); XV - коэффициент теплопроводности воздуха; l - ширина заготовки; Pr - число Прандтля для воздуха; Gr=(gl³ в AT)/v² - критерий Граст-гофа; v - кинематическая вязкость воздуха; в -коэффициент температурного расширения воздуха. Физические константы определяются при средней температуре Тср=0,5(Т + Т ).

Решение дифференциального уравнения теплопроводности. Решение дифференциального уравнения (2) сводится к решению системы линейных алгебраических уравнений (СЛАУ) согласно [5, с. 48]:

(ар • T1+1 = f [a(T- -T)-a,(T -T+i)]“ +

+ (1 - f )•[aE (T-1 - Ti )-a, (T - Ti+1 )]" +(aP ^ Ti )"

где a_P = p c A X /A t , a_E = ^J -_V2 /A X , a , = ^J i _{+ V2} /A X , A t - шаг по времени; i - индексы узлов сетки по оси X (рис. 2), n - момент времени, f - весовой коэффициент.

Дискретный аналог (5) приводится к явной ( f =0), неявной ( f =1) схемам и схеме Кранка-Николсон ( f =0,5). При использовании явной схемы дифференциального уравнения теплопроводности необходимо выполнение условия (6), а при использовании схемы Кранка-Николсон -условия (7).

At <р^ с •AX2 р 2ЛAt <[р^ с •AX2 рЛ ’

Верификация математической модели процесса охлаждения. В работе [6, с.52-54] представлены результаты эксперимента охлаждения заготовки из стали 40Х толщиной 20 мм. В качестве охлаждающей среды использовалась водовоздушная смесь, истекающая из форсунки спрейера (рис. 1) с температурой 20⁰С. Начальная температура заготовки 860⁰С. На рис. 3 представлена экспериментальная зависимость температуры на поверхности заготовки T 0 ( t ) от времени и её аппроксимация.

На рис.4 приведён средний коэффициент теплоотдачи а процесса охлаждения заготовки водовоздушной смесью, рассчитанный из экспериментальных данных. Данные получены из [6] с погрешностями построения ±6⁰C для T ₀( t ) и ±140 Вт/(м^{2 0}С) для а .

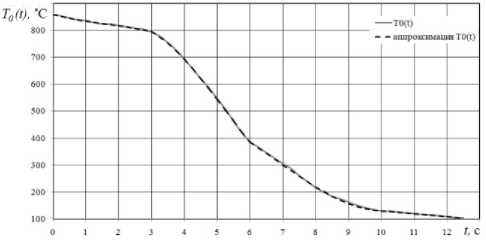
Рис. 3. Экспериментальная зависимость температуры на поверхности T ₀( t ) заготовки от времени [6] и её аппроксимация

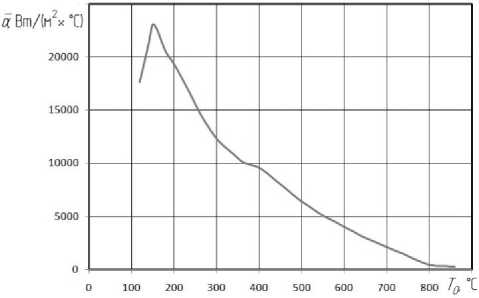
Рис. 4. Экспериментальный средний коэффициент теплоотдачи а процесса охлаждения заготовки водовоздушной смесью [6]

Экспериментальные данные температуры поверхности заготовки на четырёх участках аппроксимированы полиномами (8). Среднеквадратические отклонения при аппроксимации температуры для четырёх участков составили 5, 7, 11 и 30С соответственно.

T ( t ) = ^

• - 2,03 t ³ + 10,06 t ² - 33,3 t + 860   t g [0;3)

6,26 1 ³ - 98,46 1 ² + 954,9 1 + 448   t g [3;6)

2,746 1 ³ - 56,4 1 ² + 300,6 1 + 19 t g [6;10) - 11,0653 • t + 241 t g [10;12,5] (8)

Используя данные эксперимента (рис.3), решена обратная задача теплопроводности по явной, неявной схемам и схеме Кранка-Николсон при граничных условиях первого рода с постоянным шагом по координате NX =2 10^-5 м и времени At=1,25 10^-5 с, конечное время расчёта t=12,5 с. Теплофизические свойства стали 40Х, как и в [6], приняты постоянными для средней температуры поверхности 480 0 C согласно [7]. На рис. 5 представлены расхождения (A а ) коэффициентов теплоотдачи а_р , полученных при решении обратной задачи теплопроводности по неявной (2), явной (3) схемам и схеме Кранка-Николсон (5), а также коэффициента теплоотдачи

(1), полученного в [6], относительно среднего коэффициента теплоотдачи а (рис. 4).

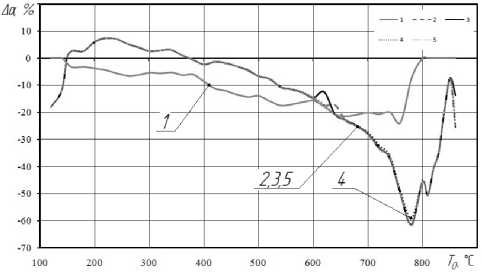
Рис. 5. Расхождения расчетных коэффициентов теплоотдачи а_р относительно среднего коэффициента а _:

1 - для коэффициента теплоотдачи, полученного в [6]; 2, 3, 5 - для неявной и явной схем, и схемы Кранка-Николсон с шагом по координате AX =2 10^-5 м и времени A t =1,25 10^-5с; 4 - для неявной схемы с шагом по коорди-натеА Х =2 10^-5 м и времени A t =0,01 с

Максимальные расхождения А а (рис. 5, поз. 2-5) порядка -60%. Это объясняется погрешностями построения и погрешностями в аппроксимации температуры и коэффициента теплоотдачи, а также приближёнными значениями экспериментального среднего коэффициента а . Расхождение коэффициента теплоотдачи, полученного в [6] с значением а составляет -24%. На основании рассчитанных коэффициентов теплоотдачи а_Р решена прямая задача теплопроводности. На рис. 6 представлены расхождения полученных, при решении прямой задачи теплопроводности, значений температур A T на поверхности заготовки для трёх схем относительно значений аппроксимации экспериментально-определённой температуры T 0 ( t ).

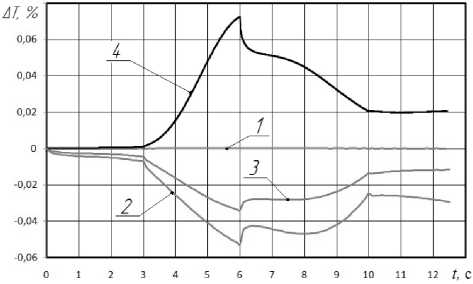
Рис. 6. Расхождения значений температур на поверхности заготовки, полученных при решении прямой задачи теплопроводности относительно T 0 ( t ):

1, 2, 3 - для неявной и явной схем, и схемы Кранка-Николсон с шагом по координате A X =2 10^-5 м и времени A t =1,25 10^-5с; 4 - для неявной схемы с шагом по коорди-натеА Х =2 10^-5 м и времени A t =0,01 с

Видно, что наиболее точное решение (рис. 6) получено по неявному методу (1). Решения прямой и обратной задач теплопроводности по явной схеме и схеме Кранка-Николсон отличаются от решений по неявной схеме по точности на -0,05% и -0,04% – для прямой задачи, на 0,4% и 2,9% – для обратной задачи; и по времени расчёта на 50% и -0,1% для обеих задач. При использовании неявной схемы нет необходимости в соблюдении условий (6) и (7), а значит возможно увеличить шаг по времени до ∆ t =0,01 с, тогда время и точность расчёта уменьшается на 99,9% и 0,08% для прямой, и на 99,7% и 1,6% для обратной задач. Решение поставленной задачи при использовании полностью неявной схемы, является наиболее предпочтительным, как по точности, так и по времени решения.

Определение температуры заготовки при одностороннем охлаждении. Рассмотрим охлаждение заготовки толщиной 20 мм и шириной 1 м из стали 40Х с начальной температурой 860⁰C. Охлаждающая среда имеет постоянную температуру 20⁰C. Вариант 1: двустороннее охлаждение – обе поверхности охлаждаются потоком охлаждающей среды в условиях вынужденной конвекции. Вариант 2: одностороннее охлаждение – одна из поверхностей охлаждается потоком охлаждающей среды в условиях вынужденной конвекции, а другая потоками воздуха с температурой 24⁰С в условиях свободной конвекции. Прямая задача теплопроводности решается по неявной схеме. Расчётное время t=12,5 c, шаг по времени ∆ t =0,01 c, шаг по координате ∆X=2 10^-5м. Физические константы и теплофизические свойства воздуха приняты согласно [2, с. 319]. Теплофизические свойства стали приняты постоянными для средней температуры поверхности 480⁰С согласно [7]. Степень черноты заготовки принимается равной ε =0,8 согласно [2, c. 330]. Для варианта 1 в качестве граничных условий используется средний коэффициент теплоотдачи α Р , определённый при решении обратной задачи по неявной схеме (∆X=2 10^-5 м, ∆ t =0,01 с). Для варианта 2 на одной поверхности принимается α Р , а на другой α Σ , который учитывает коэффициент теплоотдачи излучением (3) и коэффициент теплоотдачи при свободной конвекции (4). На рис. 7 представлено изменение температуры на поверхностях и в центре заготовки при одностороннем и двустороннем охлаждении.

Видно, что при одностороннем охлаждении (вариант 2) температура в центре Т цС 2 металлической заготовки в 1,7 раза больше, чем при двустороннем охлаждении (вариант 1); а температура на поверхности, охлаждающейся в условиях свободной конвекции больше в 6 раз.

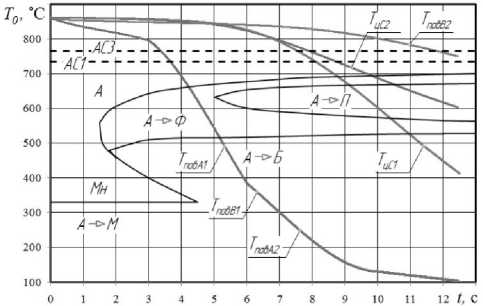
Рис. 7. Изменение температуры на поверхностях и в центре заготовки при одностороннем и двустороннем охлаждении:

Т_{повА 1}, Т_{повВ 1}, Т_{цС 1} – температуры на поверхностях А и В (рис. 1) и в центре заготовки при двухстороннем охлаждении (вариант 1); Т повА 2 , Т повВ 2 , Т цС 2 – температуры на поверхностях А и В и в центре заготовки при одностороннем охлаждении (вариант 2)

Это связано с тем, что коэффициент тепл о отдачи при свободной конвекции мал ( « св = 8,3Вт/м² - ° с ) по сравнению с коэффициентом α Р при вынужденной конвекции (рис. 4, 5). В дальнейшем планируется совершенствование математической модели, а именно: учёт изменяющихся теплофизических свойств заготовки под влиянием температуры и фазовых переходов в материале.

Выводы: приведена математическая модель процесса охлаждения стальных заготовок. Отличия при сопоставлении расчётных значений с экспериментальными составили 0,08% для температур Т и от 20 до 60% для коэффициентов теплоотдачи α . Показано, что решение задачи охлаждения заготовки при использовании полностью неявной схемы по сравнению с явной схемой и схемой Кранка-Николсон является наиболее предпочтительным, как по точности, так и по времени. Определены изменения температуры заготовки из стали 40Х, как при одностороннем, так и при двухстороннем охлаждении, по значениям которых возможна оценка фазовых переходов в материале.