Математическая модель процесса поражения летательного аппарата управляемыми ракетами с оптико-электронными системами наведения матричного типа

Описание математической модели

Математическая модель процесса поражения летательного аппарата разработана с использованием результатов, полученных в [3, 4]. Относительное движение ракеты и воздушной цели (летательного аппарата) рассматривается в абсолютной системе координат OXYZ с проекциями на горизонтальную XOY и вертикальную YOZ плоскости (рис. 1). Самолет движется прямолинейно со скоростью V С параллельно оси OY на высоте Z С . Ракета наводится на воздушную цель со скоростью V R . Составляющая вектора скорости в горизонтальной плоскости равна V_Rn . Текущая дальность между ракетой и целью определяется выражением:

D р-ц = V ^X R ^{+ (Y} R - ^Y C )^{2 +} ( ^Z R - Z C )² ,                               ⁽¹⁾

где X R , Y R , Z R - координаты ракеты, Y_C, Z C - координаты воздушной цели ( X C =0), причем Y_C = V_Ct, где t – время моделирования.

Тогда в соответствии с принятой пространственной схемой взаимного положения ракеты и цели ориентация ГСН с МФПУ в горизонтальной и вертикальной плоскостях определяется значениями углов θ_G и φ_G , углы наклона вектора скорости составляют θ_M и φ_M , углы наклона линии дальности «ракета-цель» равны θ D и φ D , а сигналы рассогласования по азимуту и углу места равны Δ θ и Δ φ . Обобщенная структурная схема математической модели представлена на рис. 2.

На рис. 2 использованы следующие обозначения: Fk – частота обновления информации о значениях сигналов рассогласования по азимуту и углу места (частота кадров МФПУ); ^G, Фо — измеренная ГСН угловая скорость вращения линии визирования цели; KG, TG - коэффициент усиления и постоянная времени передаточной функции замкнутой петли ГСН; T1, Т2 -постоянные времени передаточной функции корректирующего фильтра; Kn – навигационная постоянная контура самонаведения ракеты; Wmax - максимальное значение боковой перегрузки ракеты; T3, ξ – постоянная времени и коэффициент демпфирования передаточной функции ракеты, стабилизированной автопилотом; Wg, Wv - составляющие боковой перегрузки ракеты gv по горизонтальной и вертикальной плоскостям; Nз – число ЛТЦ в залпе; Tз – интервал между

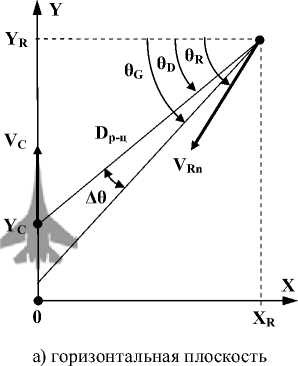
Рис. 1. Система координат движения ракеты и воздушной цели

моментами отстрела ЛТЦ в залпе; N . - число залпов в серии; T_c - интервал между залпами в серии; N п – число серий в последовательности; T п – интервал между последовательностями.

Модель формирования фоноцелевой обстановки (блок 1) обеспечивает расчет текущих координат воздушной цели Y C , Z C и координат точки прицеливания ИК ГСН ракеты в соответствии с выражениями:

X p = X R + D р-ц ^cos( ^ G )cos( - /2 ^- 9 g );

Y_tp = Y r + D cos( ^ G ) sin( ^ /2 — 9 g );                                    (2)

p            р-ц

Z_tp = Z_R + D р sin( ^ _G ).

Далее в блоке 1 методами компьютерной графики формируется изображение фоноцелевой и помеховой обстановки и рассчитываются углы наклона линии дальности между ракетой и целью по азимуту и углу места:

X_D                 Zd - Ze

⁹ D = arctg (    ^R ); ^ d = arctg (           _).                  (3)

Yr — Y C             X 2r + ( Y R — Y C )²

На рис. 3 представлены примеры изображений фоноцелевой и помеховой обстановки, формируемые ИК ГСН ракеты на различных дальностях при атаке с задней полусферы (азимут атаки: +140 град, угол места: –5 град) в условиях отстрела ЛТЦ (дальность начала отстрела – 2500 м), а на рис. 4 – при атаке с передней полусферы (азимут атаки: +15 град, угол места: +5 град).

Алгоритм селекции цели

В блоке 1 реализован алгоритм селекции цели матричной головкой самонаведения в условиях помех, представленный в [5]. Повышение помехозащищенности ГСН обеспечивается за счет морфологического анализа изображений, получаемых ГСН, и формирования маски строба, исключающей из дальнейшей обработки области изображения объектов, не имеющих при-

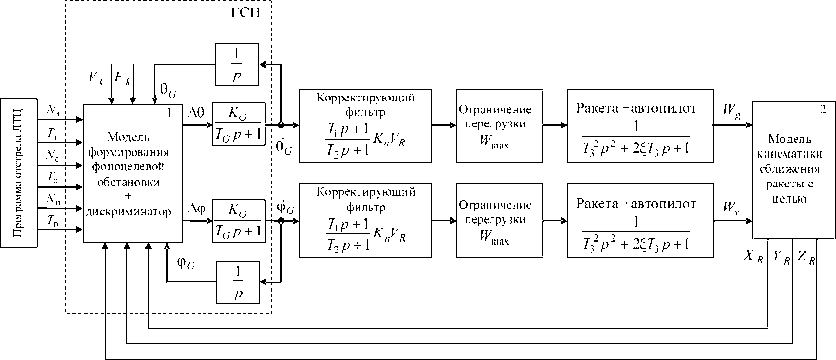
Рис. 2. Обобщенная структурная схема математической модели

D _р-ц =1500 м

D _р-ц =1000 м

D _р-ц =500 м

D _р-ц =200 м

Рис. 3. Примеры изображений ИК ГСН при атаке с задней полусферы

D _р-ц=500 м

D _р-ц =200 м

Dр-ц=1500 м       Dр-ц=1000 м рц              рц

Рис. 4. Примеры изображений ИК ГСН при атаке с передней полусферы знаков цели. Сформированное изображение маски строба используется для определения координат цели светоконтрастным или корреляционным дискриминатором. Пример формирования маски строба при обработке кадра изображения ИК ГСН ракеты в результате отстрела залпа из 20 ЛТЦ представлен на рис. 5, который наглядно демонстрирует алгоритм работы решающего устройства схемы помехозащиты при наличии изображений ложных целей (белым выделен прямоугольник, ограничивающий изображение контура цели с наибольшей площадью и эксцентриситетом).

Наконец, модель дискриминатора блока 1 обеспечивает расчет в соответствии с заданным алгоритмом обработки изображения МФПУ сигналов углового рассогласования по азимуту и углу места между линией дальности и линией визирования ГСН с частотой F_k :

Δθ=θD-θG;

Δϕ=ϕD-ϕG.

Для упрощения модели передаточная функция ракеты с автопилотом представлена колебательным звеном [6]. Выбор постоянных времени передаточной функции корректирующего фильтра контура самонаведения должен выполняться при отладке модели исходя из условия минимизации статистических характеристик промаха в беспомеховой обстановке [7].

Структурная схема модели кинематики сближения ракеты с целью (блок 2 на рис. 2) представлена на рис. 6, где 6 R ₀ , ф_{R 0} - начальные значения углов наклона вектора скорости ракеты; X_{R 0} , Y R ₀ , Z R ₀ - начальные координаты ракеты.

R

^B стр

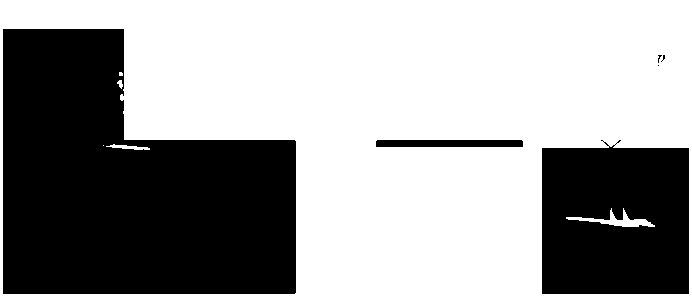
Рис. 5. Пример формирования маски строба в ИК ГСН с МФПУ

R, ^B бин

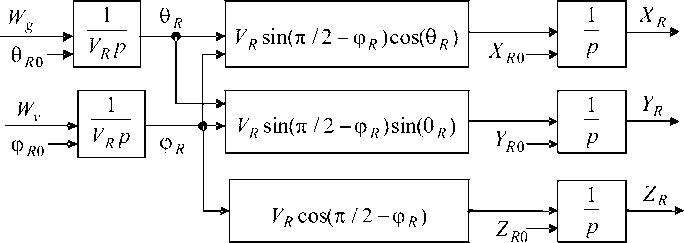
Рис. 6. Модель кинематики сближения ракеты с целью

Разработанная математическая модель реализована в среде MATLAB R2008a c использованием пакетов Image Processing Toolbox 5.2, Simulink 6.4, MATLAB Compiler 4.4 [8, 9].

Результаты проверки точности моделирования

Отладка математической модели проводилась при следующих фиксированных значениях параметров: D 0 =5000 м (начальная дальность ракеты до цели); A t =0,001 с (шаг моделирования); V R =600 м/с; F k =100 Гц; K G =100 1/c; T G =0,004 c; W max =100g; T 3 0,3 с; ξ=0,7. В ходе моделирования варьировались значения скорости воздушной цели V_c , навигационной постоянной контура самонаведения ракеты K n , начальные значения углов наклона вектора скорости ракеты 6 R ₀ , ф_{R 0} , которые равны углам атаки цели в горизонтальной и вертикальной плоскостях, и соответству-

V 7 тт ющие им начальные координаты ракеты: XR0, YR0, ZR0. Постоянные времени T1, Т2 передаточной функции корректирующего фильтра уточнялись при изменении Kn для обеспечения устойчивости контура самонаведения.

Оценка защищенности летательного аппарата с использованием разработанной модели выполняется на основе анализа величины промаха ракеты H в условиях реализации заданного алгоритма отстрела. Величина H соответствует минимальной величине пролета ракеты относительно центра масс цели.

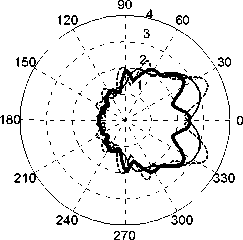
а) ϕ _{R 0} =0 град;

Рис. 7. Зависимости промаха ракеты от ракурса атаки ( V С =400 м/с)

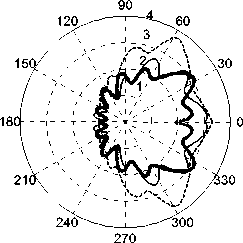
б) ϕ _{R 0} =20 град

Для обеспечения точности получаемых результатов выполнен анализ точности моделирования процесса наведения ракеты на воздушную цель по результатам моделирования атак с различных ракурсов и расчета систематических ошибок наведения. На рис. 7 изображены графики зависимостей промаха ракеты (в метрах) от углов атаки в горизонтальной плоскости 0 R ₀ (в градусах), рассчитанные для значений углов атаки в вертикальной плоскости ф_{R 0} , соответствующих 0 град и 20 град. Сплошной тонкой линией на рис. 7 обозначены зависимости, полученные при K n = 4, сплошной жирной – при K n = 5, пунктиром – при K n = 6.

Анализ полученных зависимостей показывает, что наибольшие значения промаха ракеты относительно цели достигаются при моделировании процесса наведения с передней полусферы. При углах атаки ±60 град максимальные значения промахов ракеты составляют 3 м, что объясняется, очевидно, дискретным характером работы МФПУ и большим значением поперечной составляющей скорости воздушной цели. В то же время при моделировании атак с задней полусферы значения промахов ракеты лежат в пределах 1 м. При увеличении углов атаки в вертикальной плоскости систематические ошибки наведения ракеты с K_n = 6 возрастают до 4 м. Наименьшие значения промахов ракеты в широком диапазоне углов атаки цели достигаются при K_n = 5, что указывает на целесообразность выбора при моделировании именно этого значения навигационной постоянной.

Выводы

Таким образом, разработана математическая модель процесса поражения летательного аппарата управляемыми ракетами с инфракрасными головками самонаведения матричного типа, обеспечивающая расчет координат траектории и значений промахов ракеты относительно цели в условиях функционирования устройств отстрела ложных тепловых целей. В модели учтены основные особенности формирования изображений фоноцелевой и помеховой обстановки матричным фотоприемным устройством, дискретный характер процесса формирования команд управления головкой самонаведения, а также реализован помехозащищенный алгоритм обработки изображений на основе анализа морфологических признаков. Показано, что при моделировании атак воздушной цели с задней полусферы систематическая составляющая промаха ракеты относительно центра тяжести цели, характеризующая точность моделирования, не превышает 1 м. Определены параметры контура самонаведения ракеты, при которых обеспечиваются минимальные систематические ошибки моделирования атак высокоскоростных воздушных целей с передней полусферы.