Математическая модель процесса управления скоростью движения асфальтового вибрационного катка

Строительство дорожных покрытий нежесткого типа в Российской Федерации является важной народно-хозяйственной задачей. Главные недостатки российской дорожной отрасли – малое количество и низкое качество автомобильных дорог с асфальтобетонным покрытием. Значительного улучшения качества строительства асфальтобетонных дорожных покрытий, с уменьшением до 50 % всех дефектов и разрушений [1, 2], можно добиться за счет качественного уплотнения асфальтобетонной смеси (АБС). Отряд дорожно-строительных машин по укладке и уплотнению АБС включает асфальтоукладчик и звено катков соответствующих типов и марок.

Известны научные и практические данные [3, 4]: чем выше плотность асфальтобетонного покрытия после укладчика, тем ровнее и долговечнее готовое покрытие. При устройстве асфальтобетонного покрытия с применением горячих смесей их температура является основным стохастическим фактором, значительно влияющим на рабочий процесс уплотнения и эксплуатационные показатели покрытия.

Наибольшее распространение в современных технологиях дорожного строительства при окончательном уплотнении АБС получили вибрационные дорожные катки. Существуют проблемы правильного выбора катка, настройки режимов его работы, от которых зависит производительность процесса уплотнения, а также окончательные показатели качества и долговечность дорожного покрытия. Конструкции уплотняющих дорожных машин, выпускаемые предприятиями, имеют высокий технический уровень.

Актуальной задачей совершенствования процесса уплотнения асфальтобетонных покрытий считается разработка системы автоматического управления на основе современных достижений науки и техники [5].

Рабочий процесс вибрационного катка направлен на достижение требуемой плотности асфальтобетонного покрытия за счет многократных воздействий вальцом (вальцами) на уплотняемый материал с повторяющимися проходами. Уплотняемая среда – асфальтобетонная смесь - характеризуется существенной нелинейностью из-за непрерывного изменения характеристик при деформации нелинейной упруговязкопластической среды, изменения температуры уплотняемого слоя во времени, процесса релаксации напряжений, температурной сегрегации и других факторов, что требует постоянного внимания со стороны оператора за управлением режимами работы вибрационного катка. Обеспечение эффективной работы дорожных катков возможно только за счет автоматизации технологических процессов. Основные проблемы: отсутствие автоматизации управления при реверсировании, плавности перехода с одной полосы на другую, учет изменения температуры при управлении процессами.

Цель научной работы - разработка математической модели процесса управления скоростью движения асфальтового катка.

Исходное математическое описание системы и постановка задачи

Каток представляет собой самоходную машину, в состав которой входят силовая установка, передняя и задняя рамы, кабина, механизм обработки кромки асфальтобетона. Рабочим органом катка (в зависимости от модели катка) является гладкий металлический валец (рис. 1) с встроенным вибровозбудителем.

Для разработки современной системы управления рабочими режимами вибрационного катка в процессе уплотнения асфальтобетонной смеси требуется проведение теоретических исследований на основе математических моделей. В статье рассмотрена математическая модель процесса управления скоростью движения вибрационного катка с учетом динамики ги-дрообъемной трансмиссии.

Разработка математической модели в пространстве состояний и теоретические рассуждения проводятся в терминах переменных состояний.

Гидроконтур привода хода. Гидроконтур привода хода вибрационного двухвальцового катка включает в себя регулируемый насос привода хода и два гидромотора.

Гидропривод вальцов катка как управляемую систему можно представить в виде двух подсистем: гидравлической и гидромеханической. Переменной состояния, характеризующей гидравлическую подсистему, выступает величина гидравлического давления P ( t ) гидравлического давления потока жидкости, создаваемая насосом относительно давления в сливном баке. Переменной состояния, характеризующей гидромеханическую подсистему, является величина и m (t ) скорости вращения вала гидромотора под воздействием давления потока жидкости.

Решение задачи в терминах переменных состояний

Уравнение состояния гидравлической подсистемы без учета ограничения на управляющее воздействие u(t ), изменяющего величину гидравлического давления P(t ),

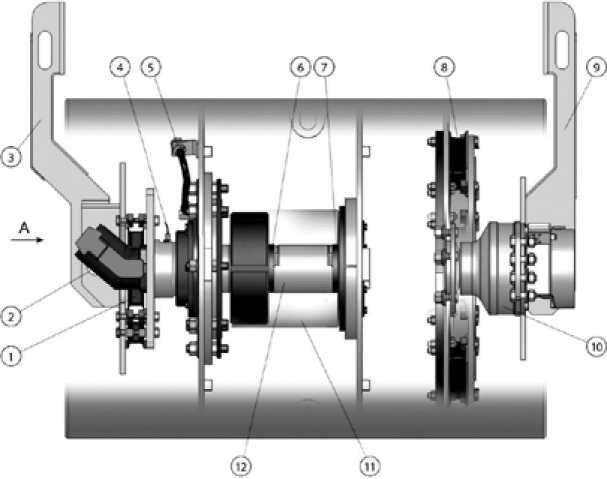
Рис. 1. Валец вибрационный (источник информации: ОАО «Раскат»): 1, 8 – амортизатор; 2, 10 – гидромотор; 3, 9 – опора; 4 – датчик частоты оборотов; 5 – заливная пробка; 6, 7 – дебаланс; 11 – корпус вибратора; 12 – вибровал

=- K     P (,)- qm. „ (,) + qPL „ (,). „ (,),                             (1)

m          e dt      Kel        Kel         Kel где Kloss – коэффициент, учитывающий потери давления в гидравлической линии при передаче, с ∙ м4/кг; Kel – коэффициент упругости трубопровода с жидкостью передающей гидравлической линии, м5/Н; P(t) - гидравлическое давление потока жидкости, Па; qm - максимальный рабочий объем гидравлического двигателя вальца, м3; qp - максимальный рабочий объем насоса, м3; юm(t) - частота вращения вала гидромотора, рад/с; иe(t) - частота вращения вала двигателя, рад/с; u(t) - управляющее воздействие.

Коэффициент упругости трубопровода с жидкостью определяется выражением [6]

K el =

п ■ d² ■ L

⁴ E el

где d и L - диаметр и длина трубопровода соответственно, м; E el - приведенный объемный модуль упругости трубопровода с жидкостью, Па:

Eflu

E el =

.

1 + J_ . Eflu,

5 ■ Е ■ pip pip

Здесь Eflu - модуль упругости жидкости, Па; Epip - модуль упругости материала трубопро-δ pip – толщина стенки трубопровода, м.

Управляющее воздействие гидравлической подсистемы u(t ) изменяет производительность насоса, может быть как положительным, так и отрицательным.

Управляющее воздействие ограничено по абсолютному значению

| u ( t )| * 1.                                                                                               (2)

Введем обозначения:

a ii = ^- Ki'" ; a i2 =^- qm- ; b ii = qp- ю e ⁽ t); x i ⁽ t ) = P ⁽ t ); x 2 ⁽ t ) = ™ m ⁽ t )•

^K el          ^K el       ^Kel

Тогда уравнение состояния гидравлической подсистемы (1) можно записать в стандартной форме (3):

dx₁(¹ )        M       М К

—-— - an ■ x i ( t ) + a i2 ■ x 2⁽ t ) + bn • u ⁽ t ).                                         ⁽³⁾

dt

Переменной состояния, характеризующей гидромеханическую подсистему, является величина скорости вращения и _m(t) вала гидромотора, изменяющейся под воздействием давления на входе, создаваемого относительно давления в сливной магистрали. Уравнение состояния записывается для одного гидромотора, эквивалентного двум параллельно работающим. Эк^вивалентность обеспечивается равенством мгновенных значений угловых скоростей вальцов при допущении об абсолютной жесткости рамы катка и достигается соответствующим изменением параметров гидромотора и его нагрузки:

d^ m lt! = q- m - bp. P ( , ) - ^„ m ( , )-± M n ( . ) ,                          (4)

dt       Jb         Jb         Jb где Jb - приведенный к валу двигателя момент инерции, кг • м2; bи - коэффициент гидромеханических потерь, зависящих от угловой скорости, H ∙ м ∙ с; bp – коэффициент гидромеханических потерь, зависящих от давления на входе гидромотора, м3.

Возмущающее воздействие, момент нагрузки M n ( t ), определяется влиянием указанного момента на угловое ускорение вальцов уплотняемой асфальтобетонной смеси при движении асфальтового вибрационного катка и зависит от режима его работы.

Введем обозначения:

a ₂₁ = q m — b P ; a 22 = - b » ; b 22 = - -1; % i ( t ) = P ( t ); x 2 ( t ) = © _m ( t ).

JbJbJb

Тогда уравнение состояния гидромеханической подсистемы (4) запишется в следующей стандартной форме (5):

dx²^ = a 21 • x i ( t ) + a 22 • x 2 ( t ) + b 22 • M n ( t ).                                     (5)

dt

В результате преобразований получена математическая модель, в терминах пространства , переменных состояния, описывающая рабочий процесс системы автоматического регулирования скоростью движения вибрационного катка. Уравнения состояния гидропривода катка как управляемой системы, таким образом, представлены в виде системы уравнений (6), два совместно решаемых уравнения (3) и (5) относительно гидравлического давления xt(t) и угловой скорости вращения вальцов x2(t) катка:

dxO dt

= a _n • x i ⁽ t) + a i2 • x 2 ⁽ t ) + b ii • u ⁽ t );

dx 2 ( t)            za            z._x ,

—-— = a 21 • x i ⁽ t ) ⁺ a 22 • ^x 2 ⁽ t ) ⁺ b 22 • M n ⁽ t ),

I dt либо в виде одного векторно-матричного уравнения состояния (7)

dX^t) = A • X ( t ) + B • U ( t ) dt

Выражения для векторов состояния X(t) и входных воздействий U(t ), матриц A , B следуют из сопоставления (6) и (7):

X ( t ) =

x 1⁽ t ) x 2⁽ t )

U ( t ) =

u ( t )

.Mn ( t )

a 21

a 12 ] . B ₌ Г b 11   ⁰

a 22 J ’      [ 0    b 22

Уравнения состояния (6), характеризующие насос и гидромотор, получены с использованием теоретических моделей научных работ [6–8]. Уравнения (3), (5)–(8) также описывают в пространстве переменных состояния поведение системы регулирования скорости движения дорожного катка по каналу управляющего воздействия с учетом его ограничений и влияния среды. Полученные уравнения состояния позволяют перейти к описанию с использованием передаточных функций (матриц).

Решение задачи с использованием передаточных функций (матриц)

Передаточная матрица, связывающая давление в гидравлической подсистеме с вектором входных воздействий, имеет следующий вид:

Г а_п  a 12 \    f i   ⁰ \     г Ь ц   о у

A m "I             I ; I "L ,| ; ^B 3 "I _п , I ; Ч m ^{- ( 1 0} ) ^; C 2.m =^{( 0} 1 ) ,

( a 21   a 22 J     1 ⁰  1 J        I ⁰   b 22 J

С 1 m ( 5 • I - A m ) ^{- 1} B 3 =

^ 11 • ( a 22 — 5 )

2 ^a 12 • a 21 ^- a ll • a 22 ^{- 5 +} a ll • ^{5 +} a 22 • ⁵

a i2 • b 22

2 ^a 12 • a 21 ^{- a} 11 • a 22 ^{- 5 + a} 11 • ^{5 +} a 22 • ⁵

Передаточная матрица, связывающая угловую скорость вращения вальцов с вектором входных воздействий, такова:

С 2 m ^{( 5} ' I ^- A m ) ^{1 B} 3 =

___________________ a 21 • b 11 ___________________ 2 .                   .

a 12 • a 21 — a 11 • a 22 - 5 + a n • 5 + a 22 • 5

______________ b 22 • ( a 11 - 5 ) ______________ 2 .                   .

a 12 • a 21 — an • a 22 - 5 + an • 5 + a 22 • 5

Используя полученные передаточные матрицы, введем передаточные функции, определяющие в динамике изменение давления в гидравлической подсистеме и изменение скорости вращения вала гидромотора в гидромеханической подсистеме.

Передаточная функция, определяющая изменение давления относительно изменения управляющего воздействия W pu ( 5 ):

w_d (S ^s ) = ——; w_d (S ^s ) = ^puv      и s s )     ^puv

______________ b ii "^{S s -} a 22) ______________ 2 s — S a ii + a 22 )" s — a i2 " a 21 + a ii " a 22

Передаточная функция, определяющая изменение давления относительно изменения воз-

ТТЛ / X мущающего воздействия Wpm (5):

W pm ^S s ) = P M^; W pm ^S s ) = 2 ,-------- A a ¹² b ^{2 2}-------------

M ^{( s} )              s ^{— (} a ii + a 22 )" s ^— a i2 " a 21 ⁺ a ll " a 22

Передаточная функция, определяющая изменение угловой скорости вращения вальцов относительно изменения управляющего воздействия W _m u ( 5 ):

w_to (S s ) = —; w» (S s ) =

ω u ω u U ( s )

_________________a 21 • bii_________________ s — (ац + a22)• s — ai2 • a21 + ац • a22

Передаточная функция, определяющая изменение угловой скорости вращения вальцов относительно изменения возмущающего воздействия W_toт ( 5 ):

W     = ^(s) ■ w =-----------b22 "(s—a11)----------- tom(s)          ; ^mm (s)    2                                             ■

M ^{( s} )             s ^{- (} а ц + a 22 ) • s ^- a i2 • a 21 + a n • a 22

Здесь P ( 5 ), Q( 5 ), U ( 5 ), M ( 5 ) являются изображениями по Лапласу соответствующих временных функций: P⁽t ), ®⁽ t ), u ⁽ t ), M⁽t ).

Вычислительный эксперимент

Определены временные характеристики соответствующих передаточных функций: импульсная переходная характеристика изменения давления в функции управляющего воздействия k_pu ( t ); переходная характеристика изменения давления в функции управляющего воздействия h_pu ( t ); импульсная переходная характеристика изменения давления в функции возмущающего воздействия k pm ( t ); переходная характеристика изменения давления в функции возмущающего воздействия h_pm ( t ); импульсная переходная характеристика изменения частоты вальцов в функции управляющего воздействия k _m u ( t ); переходная характеристика изменения частоты вращения вальцов в функции управляющего воздействия h _{m u} ( t ); импульсная переходная характеристика изменения частоты вращения вальцов в функции возмущающего воздействия k _{m m}(t ); переходная характеристика изменения частоты вращения вальцов в функции возмущающего воздействия h _{m m}(t).

Тип дорожного катка ДУ-96 [9] ОАО «Раскат» (г. Рыбинск, URL: raskat.yaroslavl.ru): вибрационный двухосный двухвальцовый с двумя приводными вальцами. Масса катка: m k 1 – эксплуатационная, m_{k 2} – конструктивная: m_{k 1} = 7200; m_{k 2} = 6600.

Диаметр гладкого вальца D b : D b = 1,07 м.

Ширина вальца L b (ширина уплотняемой полосы): L b = 1,5 м.

Линейное давление гладкого вальца соответственно P 1 b – переднего, P 2 b – заднего: P 1 b = 23000 H ∙ м^–1; P 2 b = 24000 H ∙ м^–1

Коэффициенты и их значения для уравнения состояния гидравлической подсистемы (гидравлического насоса, привода вальцов и передающей гидравлической линии): K – коэффициент упругости передающей гидравлической линии, K = 3 ∙ 10–11 el                                                                                                                                                             , el м3 ∙ ПА–1; Kloss – коэффициент, учитывающий потери давления в гидравлической линии, Kloss = 9,843 ∙ 10–11 м3 ∙ ПА–1 ∙ c–1; ωe – угловая скорость двигателя, ωe = 293,2 c–1; qp – максимальный рабочий объем насоса, qp = 35,8 ∙ 10–6 м3; qm – максимальный рабочий объем гидродвигателя привода вальца, qm = 287 ∙ 10–6 м3; Jb – момент инерции катка, Jb = 2058 кг ∙ м2.

Коэффициенты математической модели, рассчитанные на основе технических данных [5] вибрационного катка ДУ-96, таковы:

для первого уравнения состояния:

a ll = ^- K loss ■ K el ’=- 3,281^{е 1; a} 12 = ^{- 2} q m ' K el ¹ =- 1,9133 ^{- 10?} Па ^;

b11 = qp • шe • Kel-1 = 3,49904-108 кг • м-1 • с-3, для второго уравнения состояния:

a21 = 2qm • Jb-1 = 2,78912-10-7 м • кг-1; a22 =-1 с , b22 =-Jb 1 =-0,00049 кг 1 -м 2; Мnmax =14-103 Н-м.

Получены модели динамических (временных) характеристик системы управления средствами математической программной среды MathCAD.

Импульсная переходная k pu ( t ) и переходная характеристики h pu ( t )

k pu ( t ) = (175 - 10 6 + 99,25 - 10 6 • г ) • e ( ^{- 2}Д^{4 + 2,0}^⁹ ' t +

+ (175-106 -99,25-106 • г)• e(-2Д4-2,0^Д't, hpu(-) J0kpu(t)dt.

Импульсная переходная k_pm ( t ) и переходная характеристики h_pm ( t )

kpm(t) = -32,38-106 • i • e(-2,14-2,°1'i)'t + 32,38-106 • i • e(-2Д4+2,01'i)-t, hpm(t) = J0 kpm (t)dt.

Импульсная переходная k.,(t) и переходная характеристики h.u(tt k (t) = -24,28. i. e(-2,14+2,01-i)■ t + 2428. i. e(-2,14-2,01-i)■ t, h® и ( t) = Jo kюк (t ) dt.

Импульсная переходная k _m m ( t ) и переходная характеристики h _{m m} ( t )

k ® m ( t ) = ( - 242,95 - 10 ^{- 6} + 137,91 - 10 — 6 ■ i ) ■ e (^W t -- (242,95 - 10 ^{- 6} + 137,91 - 10 ^{- 6} ■ i ) ■ e ( ^{- 2,14 - 2,01 -} ' ) ^- t ,

t h® m (t ) = Jo kю m (t ) dt'

Графики временных динамических (импульсной переходной и переходной) характеристик показаны на рис. 2–5.

Полученные динамические характеристики показывают устойчивость системы управления объемным гидроприводом ходовой части дорожного катка.

Выводы

Решена задача построения математической модели процесса управления скоростью движения асфальтового катка с учетом динамики системы объемного гидропривода трансмиссии и сопротивления движению катка по дорожному покрытию. Применены современные методы разработки математической модели системы управления динамическим объектом в терминах переменных состояний и передаточных функций. Полученные решения необходимы kpu х 108, Pa х s-1 hpu х 108, Pa

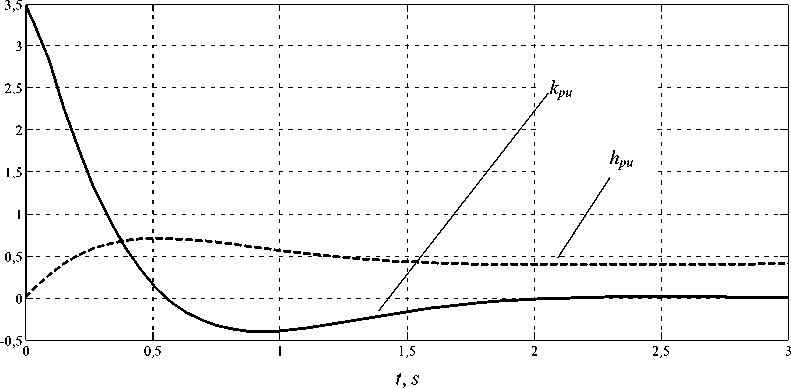
Рис. 2. Временные характеристики ku(t) и hpu(t) изменения давления в функции управляющего воздействия kpm, Pa х s-1 hpm, Pa

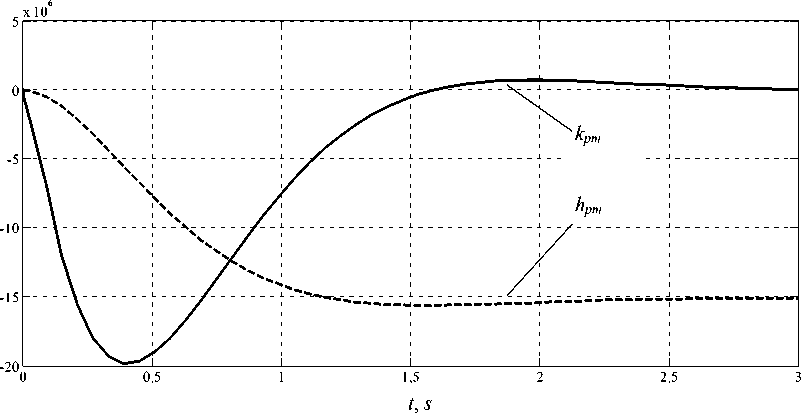
Рис. 3. Временные характеристики kpm(t) и hpm(t) изменения давления в функции возмущающего воздействия при моменте сопротивления Mn = 14000 H ∙ м kωu, s

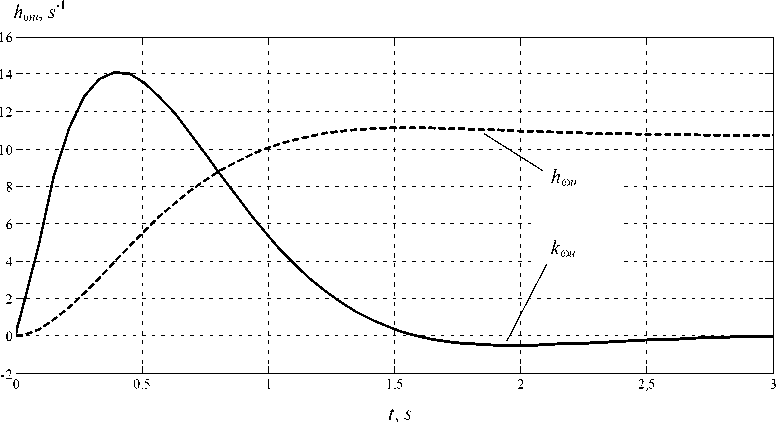
Рис. 4. Временные характеристики kωu(t) и hωu(t) изменения частоты вращения вальцов в функции управляющего воздействия kωm, s-2

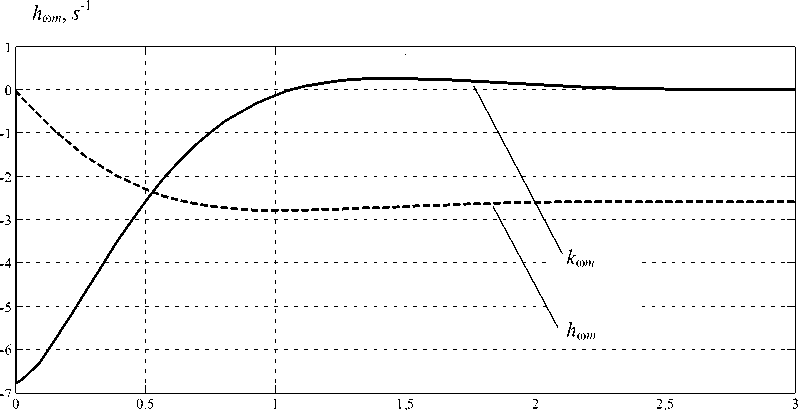
t , s

Рис. 5. Временные характеристики k„m(t) и h„m(t) изменения частоты вращения вальцов в функции возмущающего воздействия при моменте сопротивления Mn = 14000 H ∙ м при создании имитационной модели системы управления процессом уплотнения дорожностроительных материалов для дальнейшего синтеза системы автоматического управления рабочими режимами асфальтового вибрационного катка.