Математическая модель проектирования лесовозных автомобильных дорог с учетом климатических условий Северо-Западного региона

Лесопромышленный комплекс занимает одно из ведущих мест в народнохозяйственном комплексе Республики Коми как по объёмам товарной продукции, так и по удельному весу работающих, валютной выручке, формированию бюджетов всех уровней. Он во многом определяет социальноэкономическое состояние республики. Лесные ресурсы, как составная часть экономического потенциала Республики Коми, являются базой развития всех отраслей лесопромышленного комплекса [1].

Потенциал лесных ресурсов Республики Коми значителен. На её долю приходится 4,1% всей лесопокрытой площади России; 3,9% общих запасов леса; 4,2% запасов древесины хвойных пород; 5,3% запасов спелых и перестойных насаждений.

Генплан строительства лесных дорог РК предусматривает строительство магистральных и грузосборочных лесных дорог круглогодового действия в период с 2009 по 2017 гг. протяженностью 4430 км и реконструкцию существующих дорог протяженностью 789 км. В качестве основных грузосборочных дорог предполагается использовать дороги общего пользования.

Сегодня в Коми насчитывается 53 тыс. км лесных дорог, из которых круглогодично действуют всего 4 тыс. км. Это в сотни раз меньше показателей европейских стран и в десятки – европейских регионов России. Территории Северо-Западного региона характеризуются значительной транспортной удалённостью от мест переработки, неблагоприятными почвенно-грунтовыми условиями (заболоченность) и низким средним запасом на гектаре (100 м3 и менее). Более 70% лесного фонда не доступно для разработки в летнее время по почвенногрунтовым условиям, при этом распределение «зимних» и «летних» лесов по территории республики неравномерно.

Отличительной особенностью лесовозных автомобильных дорог, возводимых для кратковременного функционирования (ветки, усы), является то, что конструкции дорожных одежд назначаются, главным образом, из условий обеспечения проезда транспортных средств [2].

Дорожная одежда – инженерная конструкция из нескольких слоев различных дорожно-строительных материалов, предназначенная для движения автотранспорта. Дорожное покрытие – одно-или многослойная верхняя часть дорожной одежды, воспринимающая нагрузки от транспортных средств и защищающая основание от воздействия климати- ческих факторов. В представленной работе рассчитывается минимальная требуемая толщина всей дорожной одежды для ограничения глубины развития колеи некоторой величиной, допустимой по условию проходимости расчетных автомобилей. В связи с этим, расчетная схема таких дорожных одежд должна учитывать возможность значительного накопления остаточных деформаций в подстилающем грунте основания насыпного слоя.

Экспериментальные исследования армированных геосинтетическими материалами дорожных одежд лесовозных автомобильных дорог, где минимально необходимая толщина насыпного слоя назначается из условия проходимости и допускается сравнительно большая колея, позволили выявить схемы деформирования таких конструкций (рисунки 1, 2).

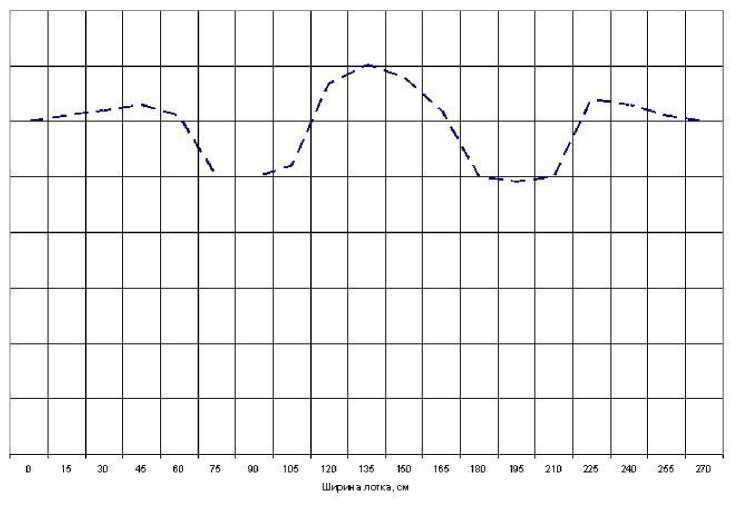
Рис. 1. Схема деформирования армированной дорожной одежды.

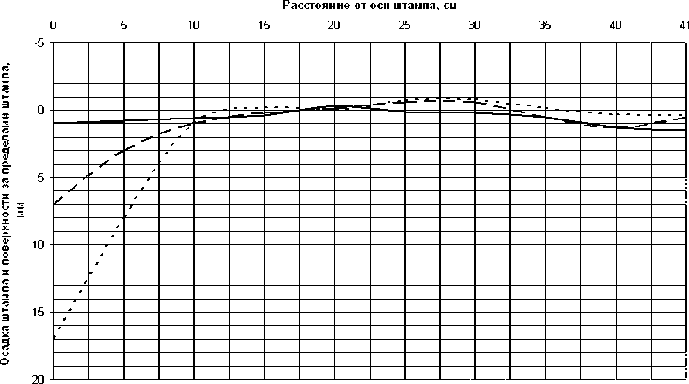
|----Ступень нагрузки №3 (0,3 МПа) — — Ступень нагрузки №2 (0,2 МПа) -Ступень нагрузки № 1 (0,1 МПа) |

Рис. 2. Схема деформирования геосинтетического материала за пределами штампа по результатам экспериментальных исследований.

Проведенные эксперименты показали, что работа конструкций в условиях одно- и двухштампового нагружения отличаются.

По одноштамповой схеме несущая способность армированной конструкции составляет всего 3,4 кгс/см2 , но при проезде транспортного средства предельное состояние конструкции не достигается даже при многократных проездах техники. Это объясняется тем, что благодаря георешетке в работу включается большая площадь основания – в «колейной» зоне и между колесами соседних осей. После 30 проходов техники конструкция, армированная георешеткой, остаётся работоспособной и имеет удовлетворительные транспортно-эксплуатационные показатели.

При двухштамповой схеме нагружения, моделирующей одновременное воздействие на дорожную одежду обоих колес оси автомобиля, несущая способность армированной конструкции значительно возрастает. Объясняется данный факт возникновением так называемого «анкерного» эффекта, когда включается в работу часть гео-синтетического материала в «межколейной зоне», т.е. в зоне защемления геосинтетики между колесами автомобиля.

Таким образом, для учета влияния георешеток на напряженно-деформированное состояние дорожных одежд и подстилающего грунтового основания, работающих в стадии накопления значительных остаточных деформаций, рассматривается условие равновесия слоя зернистого материала и георешетки на винкле-ровском (упругом) основании с шероховатой поверхностью в условиях двухштампового нагружения (рис. 3). Задача состоит в определении функции прогиба армированного слоя (положения равновесия).

В расчетной схеме обосновано использование винклеровского основания. В работах [2, 3] сделаны выводы, что в большинстве случаев кривые осадок поверхности грунтов, построенные на

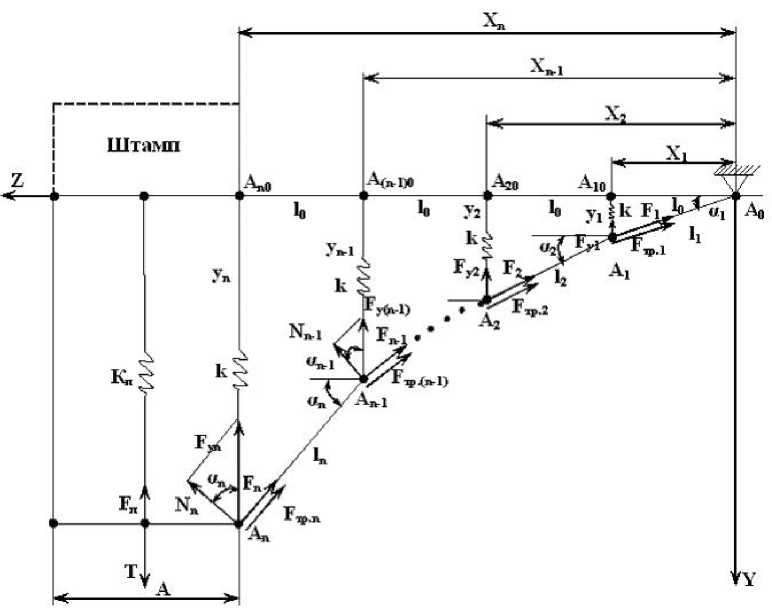
Рис. 3. Расчетная схема условия равновесия слоя зернистого материала и георешетки на винклеровском (упругом) основании с шероховатой поверхностью в условиях двухштампового нагружения.

основе модели линейно-деформированного полупространства, дают сходимость с результатами экспериментов лишь при малой влажности грунта, что типично для летнего периода и для грунтов, незначительно меняющих влажность в течение года. При влажности грунта W > 0,75W t , что особенно характерно для расчетного периода, распределительная способность грунта невелика, и поэтому модель Винклера наиболее точно отражает деформации грунта. Модель линейно-деформируе-мого полупространства может быть использована при благоприятных грунтовых условиях в III, IV и V дорожно-климатических зонах.

Предпосылки математической модели:

• 1.    Георешетка представлена механической системой, состоящей из n продольных и m поперечных упругих стержней, лежащих на шероховатой упругой поверхности и растягиваемых силой Т , приложенной со стороны штампа. Соединение стержней – шарнирное без трения.

• 2.    До нагружения штампом с силой Т стержни занимают горизонтальное положение. Длина стержней до деформации равна l 0 . Коэффициент трения – скольжение стержней о шероховатую поверхность – равен f. Параметр относительной жесткости стержней равен с = Е см F / l 0 , где Е см – модуль упругости геосинтетического материала, F – площадь поперечного сечения стержня. Упругая поверхность под георешеткой моделируется N пружинами с коэффициентами жесткости k, а упругая поверхность под штампом имеет коэффициент жесткости (постели) К П .

• 3.    Допускается что шарниры А 1 , А 2 ,..., А п при нагружении перемещаются только по вертикали. Тогда число степеней свободы рассматриваемой механической системы равно числу стержней.

• 4.    Задача при двухштамповой схеме нагружения является симметричной, поэтому она сводится к одноштамповому нагружению.

• 5.    В качестве обобщенных координат принимаем углы α 1 , α 2 ,…, α n , которые образуют стержни с осью х после нагружения системы силой Т .

q 1    ^a i , q 2

a₂ ,...,q_s = a n

Для определе- ния положения равновесия механической системы, которое она займет после нагружения силой Т, воспользуемся принципом возможных перемещений в обобщенных силах. Для этого следует составить выражение возможной работы и приравнять ее к нулю.

Q i • 8q i + Q 2 • Sq 2 + .Q • 8q n = 0 , (2)

где Q 1 , Q 2 ,..., Q n – обобщенные силы, соответствующие выбранным обобщенным координатам;

δq ₁ , δq ₂ ,…, δq_n – вариации обобщенных координат.

Поскольку вариации обобщенных координат произвольны и независимы друг от друга, то равенство (2) выполняется при условии:

Q i = 0 Q 2 = 0 ,...,Q = 0 .       (3)

Выразив каждую из обобщенных сил Qj че- рез обобщенные координаты a 1, a 2,_, a n, полу- чим систему N нелинейных алгебраических урав- нений:

^Q i ( ^a _P ^a ₂,... ^{, a} n ) = 0

Q 2 ( ^a ₁, ^a 2 ,..., ^a n ) = 0 >  .

Таким образом, задача заключается в нахождении обобщенных сил, как коэффициентов при вариации обобщенных координат в выражении возможной работы и решении системы уравнений (4).

К каждому из шарниров А 1 ,А 2 ,..., А п (рис. 3)

приложены силы: F1 , F2 ,..., Fn со стороны растя- нутых стержней, силы упругости Fó1 , Fó2 ,..., Fón , силы трения Fòð1, Fòð2 ,…, Fòðn . Кроме того, будет приложена сила упругости грунта Fn = kn ■ yn (под штампом). К участку сетки под штампом приложена сила Т.

Силы, растягивающие стержни, равны: Fi = c ■ X1,; F2 = c ■ X2  Fn = c ■ Xn, где X1 = l1 — l0; X2 = l2 — l0,., Xn = ln — l0 - удлинения стержней;

l 1 , l 2 , ..., l n – длина стержней после деформации.

Силы упругости пружин:     F₀₁ = k ■ o₁ ,

F -к- 6 F -к-6 Fo2 k 02 ,., Fon k o1 n , где ó1 , ó2 ,…, ón – ординаты точек А1, А2,..., Аn, равные удлинениям пружин.

Силы трения скольжения определяются по закону Кулона:

F oa 1 = f ■ F o i ■ ^{cos a} i ;

^F66 2 = ^f ■ ^Fo 2 ■ cos ^a 2 ,., ^Foan = ^f ■ ^Fon ■ cos ^a n .

^F 0 1 = ^kl 0 ^tg « 1

F o 2 = ^kl 0 ( tg ^a 1 ⁺ tga 2 )

F on = ^kl 0 ⁽ tg ^a 1 ⁺ tga 2 ⁺ ... ⁺ tg« n ) , Отсюда силы трения скольжения:

F oa 1 = fkl 0 tga 1 cos a 1

F

òð 2

òðn

* . (8)

= fkl ₀ ( tga ₁ + tga ₂ ) cos a ₂

= fkl 0 ( tga 1 + tga 2 + ... + tga n ) cos a n

* . (9)

Сообщим рассматриваемой механической системе возможные перемещения: δα ₁ , δα ₂ ,…, δα _n , вычислим возможную работу всех приложенных к ней сил и приравниваем её к нулю:

T 5 0n — Fn 5 yn — Fy 1 5 y 1

^— ... ^{— F}yn ^{5 y}n

—  —

...

—

F_{y 2} δ y ₂

—  —

...

F₁ 5X ₁ — F2 5X 2 —

... — Fn 5X n

—

—

F_{oa 1} ■ cos a ₁ ■ 8 x ₁

^— ... ^{— F}66n ■ ^{cos a} n

—

—

F_{oa 2} ■ cos a ₂ ■ 5 x ₂

—  —

...

, (10)

■ 5 xn

—

Foa 1 ■ ^{sin a} 1 ■ ⁵ 1

—

^F66 2 ■ ^{sin a} 2 ■ 8 y 2

—

.

—

..

Foan ■ ^{sin a} n ■ ⁵ Уп = ⁰

dx

5xx =----5ax dα1

= 0

Реакция грунта под штампом: F n = k_n ■ y_n .

Выразим координаты точек приложения сил

А 1 , А 2 ,..., А n через обобщенные координаты:

δ y ₁

dy

=----5a- dα1

= 1 0

δα ₁ cos ² α ₁

δ x ₂

X1   l0; y 1   l0 ' tgai x 2 = 2'l0; У 2 = l0 '(tgai + tga 2 )             * .

x n = n ' ^l 0 ; У п = ^l 0 ' ( tg ^a i + tg ^a 2 + -tg ^a n — 1 1

dx

=----5a t dα1

dx

+-- 5a ₂ = 0 d α ₂

δ y ₂

dy

= —^L 5a _t d α ₁

dy

+--- 5a ₂

d α ₂

*

. (11)

Найдем удлинение стержней:

^X 1 = ^l 0 ■ yf^ + tg^^i ^{— l} 0

^X 2 = ^l 0 ■ V ^{1 + tg 2 a} 2 ^{— l} 0 * .

^X n = ^l 0 ’ V ^{1 + tg} 2 ^a n ^{— l} 0

Тогда силы, растягивающие стержни, будут

равны:

F =

1 + tg ² a ₁

—

= 1 0

δα ₁ cos ² α ₁

5 x n = ⁰

/

5 У п = l 0

k

F =cl

2 2     cl 0

1 + tg 2 a ₂

—

>

.

Fn

^{1 +} tg 2^a„

—

/

cl 0

—

k

cos α _n

Определим силы упругости пружины:

+ l0

δα ₂ cos ² α ₂

δα ₁ cos ² α ₁

δα

+--2--+... + cos2 α2

δα _n cos ² α _n

Найдем вариации удлинения стержней:

d λ

5X1 =----oa1 = l( dα1

sin α ₁

= l 0      2

cos ² α ₁

δα ₁

tg α ₁ δα ₁

д/1 + tg a ₁ cos a ₁

5X₂ = -^2- 5a₂ = l, ² d α ₂    ²

sin α ₂

= l 0      2

cos ² α ₂

tg α ₂ δα ₂

1 + tg² a ₂ cos ² a ₂

>

.

δα ₂

5X n = d^^ 5a n = l, d α _n

n

tg α _n δα _n

⁰22 f ^{1 +} tg ^a n ^{cos a} n

sin α _n

¹ 0        2

cos ² α _n

δα _n

Значения сил (7) – (9) и вариаций (11) – (12) подставим в выражение (10).

— kl _о ( tga 1 + tga ₂ ) x

Tl

Tl ₀

к

δα ₁ cos ² α ₁

δα

+—7 cos 2

α ₂

δα

+... +---Tn— cos 2 αn

—

cos² α ₁

— ... — kl _о ( tga 1 + tga ₂ + ... + tga. ) x

—

K . l о ( tga_x + tga 2 + ... + tga n ) x

cos² α ₁

— K.l о ( tga 1 + tga 2 + ... + tga. ) x

X

к

δα ₁ cos ² α ₁

δα

⁺—7-cos ² α ₂

δα

+... +-----.

cos ² α _n

—  —

...

cos² α ₁

—

cl о (V1 + tg ² a .

—

sin α

1)----2--fklоtgax X cos 2 α1

—

..

.

—

kl о tga i к

cos

l 0

—5a 1 — kl 0 ( tga 1 + tga ₂ ) I x a               7

x cos a 1

sin α ₁

cos ² α ₁

— fkl _о ( tga 1 + tga ₂ ) cos a ₂ x

X

l 0

к cos ² a ₁

δα ₁

+

^{l 0}    δα ₂

cos ² α ₂

x sin a ₂

—  —

...

cos ² α ₁

—

... — fkl о ( tga 1 + tga 2 + ... + tga. ) x

—

... — kl 0 ( tga 1 + tga ₂ + ... + tga n ) x

x cos a. sin a. —-— cos² α

- ] 5a _t + [ T I

cos² α ₂

—

kl _о x

X

' l 2— cos² a 1

δα ₁

l 0                    ^

+--2----5a 2 +... + cos a 2

—

X

cos² α ₂

— ... — kl о x

+ ... +

к

l 0 cos ² α _n

δα _n

7

x ( tga 1 + tga ₂

⁺ ... ⁺ tg ^a . )

cos² α ₂

—

K.l о X

₂         l ₀ sin α ₁

— cl о (V1 + tg a — 1)---2— 5a i cos 2 α1

—

x ( tga 1 + tga ₂

⁺ ... ⁺ tg ^a n )

cos² α ₂

—

cl _о x

— cl о (V1 + tg a 2

—

1) ■ '■ 5a 2 cos ² α ₂

x (V1 + tg² a ₂

—

—

... ^— cl 0 W^{1 + tg} 2 °

—

..

.

—

sin α

1)----₂-- fkl о tg ^a 1

cos² α ₂

cos a 1 sin a 1 x

— 1)^ 5a .

cos ² α _n

—

cos² α ₂

— fkl 0 tga 1 cos a 1 sin a 1

δα ₁ cos ² α ₁

—

cos² α ₂

—

fkl 0 ( tga 1 + tga 2 ) cos a 2 sin a 2 x

X

к

δα    δα

2               2

cos ² α ₁ cos ² α ₂

—  —

...

—

... — fkl о ( tga i + tga 2 + tga . ) x

x cos a n sin a n

' § ^ai cos² a 1

δα

⁺—7-cos ² α ₂

^

+ ... +

+ ... +

к

δα _n cos ² α _n

7

= 0

Сократим на l 0 и сгруппируем члены с δα ₁ ,

δα ₂ ,…, δα _n :

— fkl _о ( tga 1 + tga ₂ ) cos a ₂

sin a ₂ x

— ... — fk о ( tga 1 + tga 2 + ... + tga. ) cos a. x

x sin a.---— cos2 α2

] x 5a ₂ + ... + [ T I

cos² α_n

—

kl _о x

X

cos² α_n

—  —

...

— ... — kl о ( tga 1 + tga 2 + ... + tga. )

— K.l о ( tga 1 + tga 2 + ... + tga. )

xU 1 + tg 2 a_n

—

1 ) sin ^. cos² α_n

cos² α_n

—

cos² α_n

—

cos² α_n

—

cl _о x

— fkl о tga_x cos a. sin a. x

fkl _о ( tga 1 + tga ₂ ) cos a. sin a. x

cos² α_n

— ... — fkl о ( tga 1 + tga 2 + ... + tga. ) x

x cos a. sin a.----— cos2 αn

] 5a. = о

Приравняв к нулю коэффициенты при δα ₁ , δα ₂ ,…, δα _n , получим n систему нелинейных трансцендентных уравнений:

T - kl 0 tg a 1 - kl 0 ( tg a 1 + tg a 2) - ... -

- ... - kl0 (tgai + tga2 + ... + tgan )- KJ0 x x (tga1 + tga2 +... + tgan) - cl0 (^/1 + tg 2a1 - 1)x x sin a1 - fkl0 tga1 cos a1 sin a1 - kl0 x x (tga1 + tga2 )cos a2 sin a2 -... - fkl0 x x (tga1 + tga2 +... + tgan )cos an sin an = 0

T - kl 0 tg a 1 - kl 0 ( tg a ₁ + tg a 2) - ... -

• ^-    ... ^{- k}l 0 ⁽ tg ^a i ⁺ tg ^a 2 ⁺ ... ⁺ tg ^a n ^)- Knl 0 ^x x ( tg a 1 + tg a 2 + ... + tg a n ) - cl 0 U 1 + tg ² a 1

  _-

  
  

  1 ) x

  
  

x sin a 2 - fkl0 tga1 cos a1 sin a1 - fkl0 x x (tga, + tga2 )cos a2 sin a2 -... - fkl0 x x (tga1 + tga2 +... + tgan )cos an sin an = 0

T - kl ₀ tg a 1 - kl ₀ ( tg a ₁ + tg a 2) - ... -

• - ... - kl 0 ⁽ tg a ₁ + tg a 2 + ... + tg a n ) -

• ^-    Knl 0 ⁽ tg ^a 1 ⁺ tg ^a 2 ⁺ ... ⁺ tg ^a n ^{)- cl} 0 ^x

x W1 + tg a1 -1 )sin an - fkl0tga1 cos an x x sin an - fkl0 (tga1 + tga2 )cos an sin an -... -

• - ... - fkl 0 ( tg a ₁ + tg a₂ + ... + tg a n ) x

x cos a n sin a n = 0

Выводы

Представленная математическая модель позволяет рассчитать оптимальную толщину дорожной одежды, армированную геосинтетическими материалами в условиях Северо-Западного региона, удовлетворяющую требуемым условиям.

Практическая применимость теоретических расчетов даст возможность произвести прогноз полной осадки и времени консолидации основания дорожной одежды, провести проверку устойчивости основания и динамический расчет насыпи на участках дорог, армированных геосинтетическими материалами.