Математическая модель прогнозирования влияния электромагнитного поля на устойчивость функционирования радиального подшипника, работающего на электропроводящей газовой смазке

Введение. Как известно, подшипники с газовой смазкой в настоящее время широко используются в машинах вращательного движения. Анализ существующих работ показывает, что в этой области есть ряд нерешённых проблем. Это, прежде всего, проблема, связанная с аналитическим прогнозированием устойчивости функционирования радиальных подшипников, работающих на электропроводящей газовой смазке при наличии магнитного поля.

Цель настоящей работы — разработать аналитический метод расчёта радиального газодинамического подшипника, работающего на электропроводящей газовой смазке. Дать оценку влияния электромагнитного поля на основные рабочие характеристики подшипника и на устойчивость его функционирования.

Постановка задачи. Рассмотрим установившееся течение электропроводящей газовой смазки в зазоре радиального подшипника при наличии электромагнитного поля. Предполагаем, что подшипник неподвижен, а шип вращается с постоянной угловой скоростью ω.

Будем исходить из уравнений «тонкого слоя» для вязкой несжимаемой жидкости при наличии электромагнитного поля.

Основные уравнения и граничные условия. Запишем для нашей задачи уравнение движения газовой смазки, уравнение неразрывности и уравнение состояния [1]:

dP  n d2U0

- oB(E - u_e B ),

---= 0, M---1- =- dr' dr'2r

P = p ' RT , — (p ' u_r,) + 5-^ + —— (p ' u_e ) = 0, , 8 r'^V          Г Г 8 0 ^{( 0})

где u _{r -} ,u₀ — компоненты вектора скорости; Р — гидродинамическое давление в смазочном слое; E = { 0,0, E } — вектор напряжённости электрического поля; B = { B ,0,0 } — вектор магнитной индукции; σ — электропроводимость газа; ρ — плотность; R — удельная газовая постоянная; μ — динамический коэффициент вязкости; r ’, θ — полярные координаты.

Функции E ( r' ,0 ) и B ( r' ,0 ) считаем заданными, удовлетворяющими уравнениям Максвелла [2, 3]:

divB = 0, rotE = 0.                                       (2)

Эти уравнения удовлетворяются при

_            „ ф' ( 9 )

E = const , B = ——,

Г

где ф ' ( 9 ) — заданная радиальная функция.

В полярной системе координат с полюсом в центре шипа уравнения контура и подшипника приближённо можно записать в виде

Г = r₀, Г = r 1 + e cos 9,                                       (4)

где r 0 — радиус шипа; r 1 — радиус подшипника; е — эксцентриситет.

Система уравнений (1) решается при следующих граничных условиях:

и _r, = 0, u₉ = 0 при Г = r 1 + e cos 9;

P

U r , = 0, и     ш г. при r = Г о ; P ( 0 ) = P ( 2n ) = -. .

Pа

Перейдём к безразмерным переменным по формулам:

U r , = w5 u , U 9 w r . u, r = Г о + 5 r , 5 = r - Г о , p ( 0 ) = p ( 2n ) , P = P a P, p ' = p p, p = p , ф ' = фф.

Подставляя (6) в (1), с учётом (3) и (5) будем иметь с точностью до членов O I — I , O I —

I ^r 0 )     I ^r 0

d² U 1 dp . 2 d / x d / x _n —T = V^T- А ф - N Jф²,—(p u ) + — (pu) = 0, d r ² Л d9 d r^{v 7} d9^{v 7}

e и = 0, и = 0 при 1 + ncos 9; и = 0, и = -p при r = 0; п = —, δ

μωr2 где Л =  £ paδ2

параметр сжимаемости газа;

_A o5² E p*    ............ „ _

A = —;   — параметр, характеризующий напря- r02μω

σδ²φ жённость электрического поля; N = —Ат μ r ₀ ²

число Гартмана.

Точное автомодельное решение задачи. Точное автомодельное решение задачи (1)—(7) будем искать в виде:

p u = -^d ^ + U ( r ,9 ) , pu = | ^ + V (r ,9 ) , p = -—^ф0— -h h ( 9 ) = 1 + ncos9. 5 9 ^v              d r ^v '       1 + п cos 9 ^v

Подставляя (8) в (7) получим следующие выражения:

а ³Ф      ₂ 5 Ф d V ²     _21/ p dp p A ф₀

+ Nфг   +    + NфгV = ^-^- dr3       dr dr2           Л d9 h (9)

d U d V _n — + ^r = 0. d r d 9

Для решения системы уравнений (9) воспользуемся следующими условиями:

U = u(^ ) nsin9; V = U ( ^ ) ; ^ = ^ ^; V = Ф ( ^ ) ,

Подставляя (10) в (9), придём к следующей системе обыкновенных дифференциальных уравнений:

p dp = C i , C 2 , p A P 0 du d O, = 0

Λ d θ h ² h ³ h ^, d ξ d ξ ^,

[ d ³ Ф _{M 2} d Ф

_< d E^{r +} N ^ф0 d^ ^{= C} 2 , ⁴ d ² U M A

⁺ N ф 0^и = ^C i .

Граничные условия для решения системы обыкновенных дифференциальных уравнений (11) будут следующими:

~

~

Ф ' ( 0 ) = 0, ф ' ( 1 ) = 0, u ( 0 ) = 0, u ( i ) = 0, и ( 0 ) = — p , и ( i ) = 0, 1 P j и d E = 0, P ( 0 ) = P ( 2n ) = -д- •

Решая линейные дифференциальные уравнения второго порядка с правой частью (11), с учётом граничных условий (12) найдём выражения для Ф ' и U :

Ф ' = C₂

sin ( ф₀ V N E ) ( cos ( ф₀ V N ) — 1 )

sin ( Ф о V N ) N p 0

-

_ cos ( ф₀ V N ^E )    c

C + -2

²      N φ ²0        N φ ²0

sin ( ф₀ V N E ) ( cos ( ф₀ V N ) pф²₀ N + cos ( ф₀ V N ) C_i sin ( ф 0 V N ) Nф^г о

-

C i ) cos ( ф 0 V N E ) ( pN v 0 + C i ) ^^^^— — ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^—

N φ ²0

~

+ C t. N φ ²0

~

Из условия j U dE = 0 найдём C _i:

где A_i = —

N ²ф 0 ^ cos ( ф о V N ) 2

— cos

— 2N cos ( ф₀ V N ) + N + N cos ( ф₀ V N )

C = A - P , ( фо V N ) + sin ( фо V N ) ² V

—

sin ( ф₀ V N ) N ^3/2 ф₀ + sin ( ф₀ V N ) N

.

Для нахождения безразмерного гидродинамического давления приходим уравнению:

к следующему

~     ~

PdP = C l ₊ C ₊ PA P 0

Λ d θ h ² h ³ h

Интегрируя уравнение (13) от 0 до θ, будем иметь

.

P =

i + 27 ^P a j(

^P -  0 V

~     ~

^C ₊ ^C ₊ A pp ^j d _Q. h ² h³ h I

Решение интегрального уравнения (14) будем искать методом последовательных приближений, полагая в качестве первого приближения р 0 = 1. С точностью до О (Λ²) для p 1 получим следующее выражение:

- => P  P a 1

V

~

A i ^C2^ ₊4 ф 0 Ъ" h T ⁺ h 3 ⁺ — d® •

h

V

Из условия р (0) = р (2п) с точностью до О (п²) найдём С ₂:

C 2 = — 4 ф 0 — 4 .

Тогда выражение для гидродинамического давления р 1 с точностью до О (η²) примет вид:

Pi = А I- Т ^-Рд + Pa Л Ainsin® + Pa 2Л Aфоnsine ] • pa Pд

Проекции главного вектора вещества смазок W = ^ R j + R y на шип определяется формулами:

2π                           2π

R x = — г ₀ J P sin6 d 6; R_y = — г ₀ J P cos 6d6

Заметим, что в силу периодичности давления Р и чётности cosθ второй интеграл соответственно равен нулю. Первый интеграл проще вычислить по частям:

2π                                         2π                        2π

R x = — Г 0 J Pd ( — cose ) = rP cos6| 0" — Г 0 J— cos6 d 6 = — Г 0 J -^cos6 d 6.

_{0                            0} d θ             ₀ d θ

Подставляя выражение для гидродинамического давления в выражение (15), найдём выражение для несущей способности подшипника:

W = R x

( Дп + 2 Д ф о + З Д ф о П ) .

Найдём силу трения по формуле:

L =

d e = ^И⁰ ) d ⁶ =

5 0          ^б 0

2μω r ₀ δ

к

( a + A 0 ) sin ( Ф 0V N ) _1₊ Pg"

Ф₀ T N ( cos ( Ф₀ V N ) + 1 )     p^a ₂

Найдём расход смазки по формуле:

Q = pto Г о б / Ф ' ( 5 ) d =

= P to Г ,б

С₂ |— 2cos ( Ф_о^ ) N + N + cos ( Ф_о^ ) N |

N^5/2 sin ( V o V N ) Ф 0

— P ' to r . 5

С ₂ | N ^3/2ф ₀ sin ( v _o V N ) + sin ( V o V N ) N |

N ^5/2 sin ( ф о л/ N ) Ф0

.

Решение задачи об устойчивости. Решение этой задачи приводится на основе следующего безразмерного уравнения движения шипа:

d2ε dT2

d2Ф dT2 =

—

-^+ + ω² Mr ₀

R y εω² Mr ₀

—

1 Г го E к to

ω

ω

I               I dФ I

| cos Ф + E I dT I ,

. . 2 ( dE IГ dФ sin Ф — - eк dT JкdT

.

e

Здесь e =----- — относительный эксцентриситет; Т = tot; t — время; to — угловая скорость вра- ri — Г0

1/ r

I g । щения шипа; е — эксцентриситет; r — радиус шипа; М — масса шипа; to = —   ; б — радиаль- к б J ный зазор; g — ускорение силы тяжести; Rx и Ry — компоненты вектора поддерживающей силы; Ф — угол наложения.

Явные выражения для R x и R y , приведённые выше, показывают, что R x и R y существенно зависят от следующих безразмерных параметров: параметра сжимаемости газа Λ, параметра А , характеризующего напряжённость электрического поля, и параметра N , характеризующего число Гартмана. Используя выражения для R x и R y , можно получить численное решение системы (19).

Компоненты ускорения шипа

d ²ε    d ² Ф

и dT2   dT2

представляют собой явные функции параметров

d ε dФ ε, Ф , dT , dt ,

Λ, A, N . Уравнения (19) записываются в стандартной форме первого порядка и решаются с помощью многознакового метода, разработанного Гиром [4]. После получения реше- ния уравнений движения для заданных значений ε, Ф

d ε dФ

^, dT ^, dt ^,

Λ, A , N устойчивость рас-

сматриваемого движения определяется визуально по графику. Некоторые модели движения шипа приведены на рисунках 3 и 4. На рис. 3 представлено устойчивое движения шипа при следующих условиях n = 0,01; En = 0,5; “ = 2,4; Ф = 0,001; л = 0,25; A = 0,6; N = 0,4. На рис. 4 представле-0ω но неустойчивое движение шипа (е0 = 0,8;

“ = 2,5; Ф = 0,001; Л = 0,25; A = 0,25; A = 0,1; ω

N = 0,2).

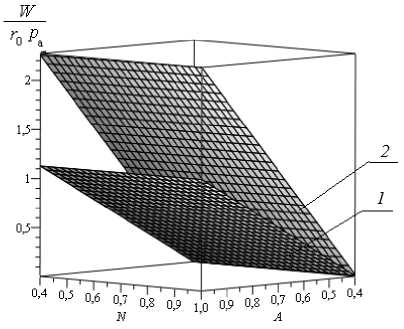
Рис. 1. Зависимость безразмерной несущей способности

W от числа Гартмана, параметра сжимаемости газа и r0pa

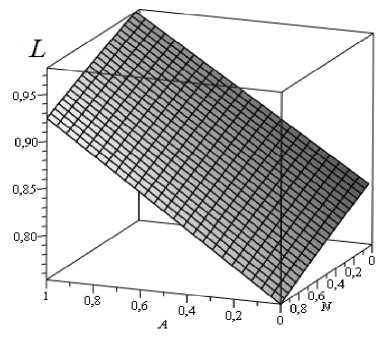
Рис. 2. Зависимость безразмерной силы трения L от числа Гартмана и параметра A , характеризующего напряжённость электрического поля

параметра A , характеризующего напряжённость электрического поля. 1 — Λ = 0,25; 2 — Λ = 0,5

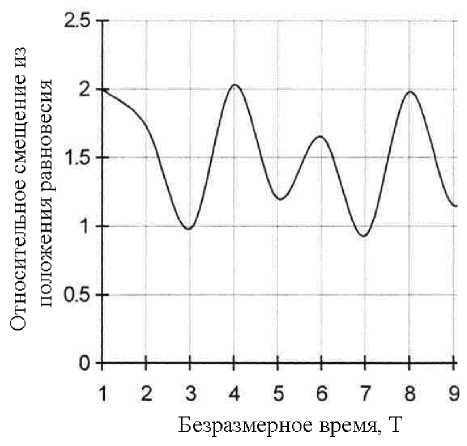
Рис. 3. Движение центра шипа при моделировании устой- чивого состояния

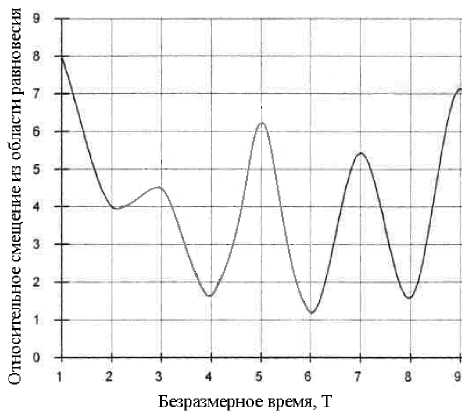
Рис. 4. Движение центра шипа при моделировании неустой- чивого состояния

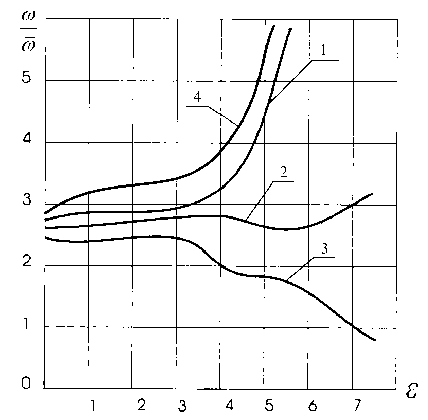
1 — η = 0,0001, А = 0, N = 0; 2 — η = 0,0007, А = 0, N = 0; 3 — η = 0,01, А = 0, N = 0; 4 — η = 0,0001, А = 0,5, N = 0,4 Рис. 5. Область устойчивости движения шипа

Результаты для некоторых значений Ф , ε, Λ, A и N приведены на рис. 5. Все точки, которые лежат ниже кривых, соответствуют устойчивому движению, а все точки, которые лежат выше этих кривых, соответственно — неустойчивому движению шипа. Графики устойчивости определяются такими точками (ω/ ω ), которые являются неграничными, т. е. соответствуют орбите шипа.

Выводы. Результаты численного анализа аналитических выражений (16)—(18) для основных рабочих характеристик радиального подшипника показывают:

— Число Гартмана не оказывает существенного влияния на несущую способность подшипника (рис. 1). С увеличением параметра А , характеризующего напряжённость электрического поля, и параметра сжимаемости газа имеет место значительное увеличение несущей способности.

— С увеличением параметра А , характеризующего напряжённость электрического поля, безразмерная сила трения возрастает (рис. 2), а с увеличением числа Гартмана уменьшается. Принимая во внимание решение для малого числа приближений, параметр сжимаемости газа не оказывает существенного влияния на безразмерную силу трения.

— С увеличением числа Гартмана расход смазки резко уменьшается. При малых значениях с увеличением параметра А , характеризующего напряжённость электрического поля, расход смазки незначительно возрастает. Принимая во внимание решение для малого числа приближений, параметр сжимаемости газа не оказывает существенного влияния на расход смазочного вещества.

— Из приведённых на рис. 5 зависимостей следует, что в случае электропроводящей газовой смазки область устойчивости движения шипа расширяется.