Математическая модель распространения загрязняющих веществ в грунте

в почву под свалкой можно рассматривать как процесс инфильтрации жидкости в грунт под действием силы тяжести и давления воды, находящейся на поверхности. Проведенные ранее исследования Костякова А.Н. и Аверьянова С.Ф. опираются на модель грунта в виде сплошной среды. В соответствии с этой моделью, в результате расчета получаются средние скорости течений, то есть скорости, осреднен-ные по некоторой площадке.

Для получения «истинных» скоростей движения жидкости в порах примем в качестве модели — модель идеального грунта. Дифференциальное уравнение движения, для рассматриваемой модели с учетом переменной массы движущейся воды имеет вид:

d У mg y dy

+ g — и dt k А + (1 - m ) y dt

(1),

здесь y - глубина проникновения жидкости в поры грунта на момент времени t, m - эффективная пористость грунта, g - ускорение свободного падения, k - коэффициент фильтрации грунта под телом свалки, А - высота слоя воды на поверхности грунта в начальный момент времени t=0. Данное уравнение представляется эпюрой с восходящей и нисходящей ветвью. Нисходящую ветвь эпюры скоростей можно аппроксимировать гиперболой

V — A • t

—

0,5 + b

Анализ уравнения (2) показывает, что первый член уравнения (вторая производная) заметно влияет на движение только в начальный, весьма короткий период времени. Пренебрежем первым членом и получим упрощенное уравнение движения жидкости, при просачивании ее в грунт.

mуdy -1 = о k A + (1 - m) y dt

Или, обозначив для удобства п=(1-т), получим dt = m , y •dy k A + n - y

Интегрируя, при начальных условиях Х0)=0, найдем:

m m • A , ,, n t =  ---y - "---rln(1 + - y)

k - n k - n A (5)

Эта формула является приближенной, поэтому для ее уточнения введем коэффициенты m mm • A , z, n x t = a--— y - p- ----2ln(1 + - y)

k • n k • n A (6)

Коэффициенты а и в находятся при обработке экспериментальных данных. Экспериментально полученная зависимость времени проникновения жидкости от глубины проникновения с использованием математического пакета Mathcad 13 аппроксимируем функцией

n t = A ■ y - B • ln(1 +---y)

^A               (7)

Расхождение между экспериментальными данными и вычислениями оценивались с помощью программы ChiSquareGoodnessOfFit-Test Maple 10. Результаты расчетов подтвердили отсутствие значимых расхождений на 0.05 уровне. В результате обработки получены значения коэффициентов А и В, которые являются функциями параметров, определяющих движение жидкости, а именно т, к, Л. n является функцией т .

Сравнивая уравнения (6) и (7), получим:

m        m -A

A = a --; B = в---k - n             k - n ²

a = A - kln ; в = B - kn .

или      m         m

a = r1 mi + r2 - k + r3 - A; в = q1 mi + q2 - k + q3 - A.

Анализ отношения в / а показал, что эти значения распределены нормально с средним значением 1,07 и дисперсией 0,1. Поэтому доверительный интервал для среднего значения 1,07+0,03.

Для определения численного значения а и в использовалась функция линейн, имеющаяся в математическом пакете Excel . В качестве нулевой гипотезы было выдвинуто предположение, что величина а не зависит от параметров т , к и А . Расчетное значение статистики получено F_ex=26,78. Критическое значение статистики - F=5,409. Расчетное значение значительно превышает критическое и нулевая гипотеза, с вероятностью 95% отвергается. Это позволяет сделать вывод о том, что существует достаточно сильная зависимость между коэффициентом а и параметрами т , к и А .

Далее была определена статистическая значимость коэффициентов разложения, которая показала, что а зависит, в основном, от высоты слоя воды на поверхности грунта и коэффициента фильтрации. Таким образом, в результате расчетов предложена формулу для определения а :

a = 0.04 -A + 25 - k - 0.2

Для получения более простой зависимости y(t) разложим правую часть уравнения 10:

m mm- A , Z1 n x t = a- ----y - P- ----rln(1 + T У)

k n k n A (₁₀)

в степенной ряд по у и удержим два члена. Получим:

, . 1 в-m 2

t = m-(в- a) у + -- ——- у

^{2 A- k} (11)

Правая часть полученного уравнения является приближенным решением. Для уточнения коэффициентов при переменной у аппроксимируем опытные данные параболой, то есть:

а и в также являются случайными величинами. Их можно представить в виде системы точек в четырехмерном пространстве с координатными осями т , к, А , расположенных на некоторой поверхности. Приближенно эту поверхность можно аппроксимировать гиперплоскостью. Уравнения этих гиперплоскостей можно записать так:

t = ry + q-y (12)

После обработки получим:

m ₍ _    \      1 _п m-y у

t = ---(Р - a)-y + - p"—— k-n               r A -k (13)

Или

t = a •

( 0.07 • m • y ² _v r -A- k

+ 1.07 •

ym / k - n )

где r — уточняющий коэффициент, позволяющий учесть остальные члены степенного ряда.

Решая относительно у, получим зависимость глубины проникновения у от времени:

• 1    r - m • A- ( в - a ) y = •               +

• 2      в" m • n

+ m ² - A ² • r ² • ( в — a )² + 4 • r - в"m " n ² " k "A- t

0-m - n

Дифференцируя (15) по времени, получим скорость инфильтрации в различные моменты времени:

V =

r • k • n - A д/[r • m • A(в - a)]2 + 4 • r • 0- m • n2 • k • A • t

После сопоставления полученной формулы с результатами лабораторных экспериментов получили, что для грунтов с однородной крупностью (первый и второй тип грунта) r соответствует 5. Приведенные выше уравнения можно применять при области изменения параметров:

• -    коэффициента фильтрации к ф от 0,05 - 10^-2 см/с до 0,01 - 10^-2 см/с,

• -    исходной величине слоя жидкости на поверхности от 5 до 15 см или слое выпадения осадков от 25 до 75 мм.

В качестве начальных условий принято, что первоначально жидкость в порах отсутствует, а жидкость, оказывающая воздействие на почву и грунт, находится в состоянии покоя, то есть отсутствует движение по поверхности. Приведенные формулы можно применять только при А> 0, далее движение жидкости становится безнапорным и применение вышеописанных формул не возможно. Для практического применения можно рекомендовать следующую последовательность вычислений характеристик движения загрязненной жидкости в грунт под свалкой:

• 1.    По формуле 10 определяется время проникновения жидкости на заданную глубину.

• 2.    По формуле 15 определяется глубина проникновения жидкости за заданный период времени.

• 3.    По формуле 16 определяется скорость

движения в заданный момент времени.

t, с

0         50        100        150       200       250

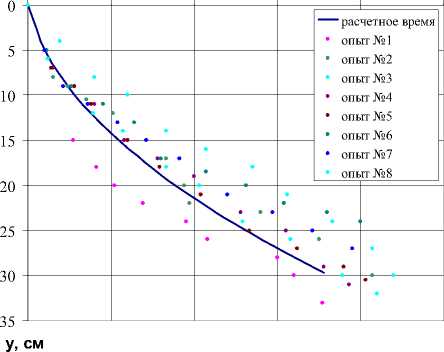
Рис. 1 Результаты расчета времени проникновения

V, см/с

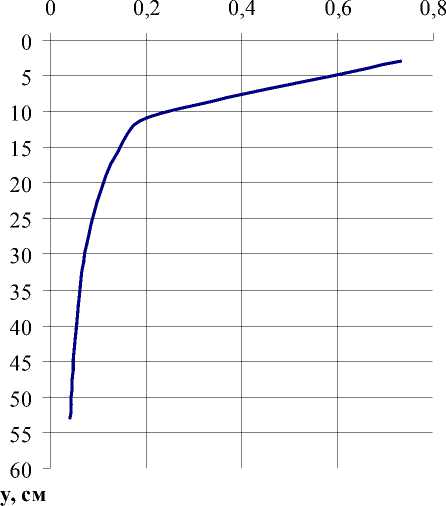
Рис. 2. Распределение скоростей проникновения жидкости в грунт (к ф = 1,1-10^-2 см/с ) при А =15 см

Для грунта с к ф =1,1-10 " ² см/с при А =5 см в результате расчетов были получены данные представленные в табл. 1. Таким образом, полученные зависимости показали приемлемую сходимость с экспериментальными данными.

Таблица 1. Результаты расчетов

Экспериментальные		Расчетные
время проникновения, с	глубина, см	время проникновения, с	глубина, см	скорость, см/с
0	0	0	0	1,399
3,45	8,82	6,17	3,4537	0,457
6,73	22,64	18,85	6,72695	0,336
10,00	43,09	38,18	10,0003	0,278
13,55	68,64	66,62	13,5459	0,240
17,27	108,27	104,92	17,2724	0,213

Выводы:

• 1.    Получена математическая модель проникновения загрязняющих веществ в грунт.

• 2.    Разработанная модель позволяет определять время проникновения жидкости на заданную глубину в зависимости от начального слоя жидкости и таких параметров грунта как пористость и коэффициент фильтрации, а также решить обратную задачу - определить

• 3.    Модель проникновения загрязняющей жидкости в грунт позволит спрогнозировать глубину загрязнения грунта под телом необу-строенной свалки.

глубину проникновения жидкости на любой момент времени, в зависимости от названных выше параметров. Модель позволит рассчитать также скорость движения жидкости на любой глубине в заданный момент времени.

MATHEMATICAL MODEL OF DISTRIBUTION THE POLLUTING SUBSTANCES IN GROUND