Математическая модель развития трещины гидроразрыва пласта в трехмерной пороупругой среде
Автор: Савенков Е.Б., Борисов В.Е.
Статья в выпуске: 1, 2018 года.
Бесплатный доступ
В настоящее время гидроразрыв пласта (ГРП) является одним из самых распространенных методов увеличения нефтеотдачи, применяемым при промышленной разработке нефтегазовых месторождений. В то же время используемые модели развития трещины ГРП являются во многом упрощенными: геометрия трещины предполагается плоской и заранее заданной, практически всегда отсутствует полноценный учет геомеханических эффектов, эволюция трещины зачастую описывается эмпирическими критериями. Несмотря на успешность применения таких моделей, их возможностей недостаточно для решения ряда важных задач разработки. В работе представлена полностью трехмерная самосогласованная физико-математическая модель развития крупномасштабной трещины гидроразрыва пласта. Модель включает в себя несколько групп уравнений, включая неизотермическую пороупругую модель Био для описания поведения вмещающей трещину среды, двумерные уравнения смазочного слоя, описывающие течение в трещине, соответствующие условия согласования на границе «трещина-среда». Геометрическая модель трещины предполагает, что она является произвольной гладкой поверхностью с краем. Эволюция поверхности трещины в ходе ее роста описывается физически обоснованными критериями на основе векторной формы J-интеграла Райса-Черепанова. Модель пригодна как для анализа непосредственно процесса развития трещины ГРП, так и для анализа вызванных наличием трещины фильтрационных и геомеханических эффектов в ходе эксплуатации скважины с ГРП. Основное назначение предложенной модели - согласованное описание процесса развития трещины ГРП в достаточно общей постановке с минимумом априорных допущений о характере протекания процесса и вместе с тем пригодное для использования на практике с применением современных вычислительных подходов. В связи с этим в работе дан краткий обзор вычислительных алгоритмов, пригодных для практической реализации модели.
Геомеханика, пороупругая среда, трещина гидроразрыва пласта
Короткий адрес: https://sciup.org/146211715
IDR: 146211715 | УДК: 519.6 | DOI: 10.15593/perm.mech/2018.1.01
Текст научной статьи Математическая модель развития трещины гидроразрыва пласта в трехмерной пороупругой среде
ВЕСТНИК ПНИПУ. МЕХАНИКА № 1, 2018PNRPU MECHANICS BULLETIN
В настоящей работе предложена связанная математическая модель развития крупномасштабной трещины гидроразрыва пласта в пороупругой среде. Гидравлический разрыв пласта (ГРП) является одним из самых распространенных методов увеличения нефтеотдачи, используемым при промышленной разработке нефтегазовых месторождений. Сущность технологии ГРП заключается в закачке в нефтеносный пласт специальной жидкости с целью создания искусственной (техногенной) трещины длиной ~ 100 м, высотой ~10 м и средним раскрытием ~5-10 мм. В результате создается соединенный со скважиной искусственный канал с большой площадью притока, который имеет высокую (на порядки превышающую пластовую) проницаемость. Это обеспечивает значительное увеличение притока пластового флюида к скважине. Инженерные аспекты технологии рассматриваются, например, в [1].
Используемые в настоящее время математические модели развития трещины ГРП в большинстве своем имеют «инженерный» характер: в них используются двумерные постановки, априорно заданные геометрические модели трещин, практически никогда не производится корректный учет геомеханических эффектов и т.д. (см., например, [1-3]. Использование таких математических моделей давно стало стандартной инженерной практикой. Однако ряд задач, связанных с динами- кой развития трещин ГРП, требует использования полных корректных (самосогласованных) пространственнотрехмерных постановок. Прежде всего к таким задачам относится анализ развития трещин в существенно неоднородном поле напряжений, индуцированном наличием соседних техногенных (например, множественный ГРП на горизонтальных скважинах) или естественных трещин, неоднородных полей давления, порожденных закачкой или отбором флюида в пласт и т.д.
Одновременно с полнотой постановки математические модели должны быть пригодны для использования на практике.
Целью настоящей работы является попытка построения такой модели. В связи с прикладной направленностью предлагаемой модели она дополнена разделом, который носит характер краткого обзора и посвящен описанию методов вычислительной математики, которые могут быть использованы при реализации модели в рамках программы-симулятора для математического моделирования ГРП в «расширенной» постановке.
Физико-математическое описание динамики трещины ГРП в ходе ее развития сводится к решению сложной связанной задачи, включающей в себя следующие системы уравнений:
-
• система уравнений пороупругости, описывающих эволюцию напряженно-деформированного состояния среды и полей давления флюида в ней в ходе развития трещины;
-
• уравнения течения жидкости в трещине;
-
• механические условия развития трещины, определяющие направление ее развития в каждой точке ее фронта;
-
• заданные на боковых поверхностях трещины условия согласования между полями давления в трещине и в среде, потоками массы, импульса и энергии, а также кинематические условия, связывающие раскрытие трещины и перемещение точек пласта.
Построенная в работе математическая модель позволяет корректно описывать согласованное распределение возмущений начального поля напряжений регионального масштаба с учетом эффектов, индуцированных процессами фильтрации при наличии добывающих и нагнетательных скважин, наличия трещины и ее развития с учетом как региональных, так и индуцированных полей напряжений, течения флюида в трещине. Модель пригодна для анализа эффектов самопроизвольного развития трещины ГРП («автоГРП») в пространственных масштабах элемента (ячейки) системы заводнения месторождения.
В качестве модели вмещающей среды используется связанная модель Био для описания возмущений начального поля напряжений регионального масштаба, вызванных присутствием и развитием трещины и эффектами фильтрации. Все основные соотношения модели приведены для неизотермического случая. Описание группы уравнений пороупругости модели основано на [4]. Отметим, что, вообще говоря, геологические среды на временных и пространственных масштабах, связанных с развитием трещины ГРП, могут проявлять пластические и/или вязкоупругие свойства. Учет таких эффектов в рамках рассматриваемой модели потребует изменения «механической» части модели Био и является скорее техническим усложнением, не меняющим принципиально структуру математической модели и способ связывания соответствующих групп уравнений. Вместе с тем при моделировании процессов развития трещины ГРП на практике зачастую используются именно линейно-упругие среды. Это связано с простотой указанных моделей и сравнительно высокой степенью надежности определения параметров среды (упругих модулей, модулей Био и критериев разрушения) в случае линейной среды.
Для описания течения флюида в трещине использованы уравнения гидродинамики в приближении смазочного слоя. Гидродинамическая модель течения дополнена уравнениями переноса энергии и позволяет производить учет неизотермических эффектов.
При описании процесса развития трещины использованы физически обоснованные критерии разрушения с учетом комбинированного режима нагружения в окрестности фронта распространяющейся трещины.
1. Модель вмещающей среды
В настоящем разделе описана согласованная математическая модель развития крупномасштабной трещины ГРП в напряженно-деформированном насыщенном пласте. Основные допущения модели: напряженно-деформированное состояние пласта основано на физически и геометрически линейной модели; задача рассматривается в неизотермическом приближении, при этом отклонения температуры от начальной предполагаются малыми; пластовый флюид является однофазным и слабо сжимаемым; динамическими эффектами (силами инерции) при описании напряженно-деформированного состояния вмещающей среды можно пренебречь (то есть процесс является квазистационарным).
Уравнения механического равновесия (уравнения закона сохранения импульса) имеют вид
V- T + p g = 0, (1)
где р = р ( х ) - плотность насыщенной флюидом вмещающей среды; g - ускорение свободного падения; T -тензор напряжений.
Описанные уравнения должны быть дополнены граничными условиями. При моделировании развития трещины ГРП граничные условия для давления можно задать как однородные граничные условия Неймана, обеспечивающие нулевой поток массы флюида, либо как граничное условие Дирихле, выражающее постоянство давления как функции времени (граница расчетной области при этом рассматривается как «контур питания»). Перемещения точек среды на внешней границе области в пластовых условиях неизвестны, по этой причине «механические» граничные условия обычно имеют вид граничных условий Неймана, которые выражают заданное значение нормальных напряжений на границе области.
В обоих случаях предполагается, что расстояние от трещины до границы области, занятой вмещающей средой, достаточно велико по сравнению с длиной трещины.
В общем случае анизотропного пороупругого насыщенного тела в линейном приближении определяющие соотношения имеют вид [4]
AT = C: E - BAp - C: AA0, Аф = B : E + N Ap - 3aфA@, где p - давление флюида; T - тензор напряжений; E = |^V ® u + (V ® u)T ] /2 - тензор деформаций; u -поле перемещений точек вмещающей среды; C = [Cijkl ] -симметричный тензор упругих коэффициентов 4-го ранга; B = |^Bij ] - симметричный тензор Био; A = ^aj J -симметричный тензор коэффициентов термического расширения; 0 - температура; ф - пористость; аф -объемный коэффициент термического расширения порового пространства; N - модуль Био, связывающий изменение пористости с изменением давления флюида; C - коэффициент теплоемкости скелета при постоянном объеме, Af = f — f) для какой-либо величины f, индексом «0» обозначены значения величины в исходном состоянии.
В случае изотропной среды имеем
C=λI⊗I+2GI, B=bI, A=αI, где λ , G – коэффициенты Ламе скелета; ε =E:I=Eii – объемная деформация; λ=K - (2/3)G; K – объемный модуль упругости.
Плотность ρ в (1) зависит от плотности скелета и флюида и пористости вмещающей среды: ρ =(1 -ϕ ) ρ s +ϕρ f , где ρ s – плотность скелета; ρ f – плотность флюида.
При деформации породы происходит изменение объема, занятого флюидом. Это изменение связано как с изменением объема скелета, так и с изменением объема порового пространства за счет деформации скелета. Уравнения закона сохранения массы флюида имеют вид
∂ mf w
+ ∇⋅ ( w m )= q , v = m = K ⋅ ( - ∇ p +ρ f g ), (2)
∂t ρf где m f – масса флюида в единице объема насыщенной среды; wm= ρfv – вектор плотности потока массы; v – скорость фильтрации, определяемая законом Дарси; ρf – плотность флюида; K – симметричный тензор коэффициентов проницаемости; q – массовая плотность источников.
Считая, что в элементарном объеме насыщенной среды скелет и флюид находятся в состоянии локального термодинамического равновесия, уравнение закона сохранения энергии (при отсутствии внешних источников энергии) запишется в виде
∂e
+∇(hfwm+qΘ)=0, ∂t qΘ=-Λ∇Θ,
где h f – энтальпия флюида; q Θ – вектор плотности теплового потока за счет эффектов теплопроводности; e – полная внутренняя энергия элемента объема насыщенной среды; e = ρ s (1 -ϕ ) es +ρ f ϕ ef ; Λ – симметричный тензор коэффициентов теплопроводности; e s f и р s f - внутренние энергии и плотности твердой и подвижной фаз.
Приведенные выше уравнения должны быть дополнены определяющими соотношениями. В дальнейшем будем считать, что отклонения от начального состояния малы и флюид слабо сжимаем, то есть
Δρ f = Δ p ρ 0 f K f
- 3 α f
ΔΘ
Δ sf
Δ p ΔΘ - 3 α f 0 + Cp , (3) ρ f Θ 0
где p – давление флюида; ρ f – его плотность; α f – коэффициент температурного расширения флюида; Θ – его температура; sf – энтропия; Cp – теплоемкость при постоянном давлении; Kf – объемный модуль сжатия флюида. Далее будем считать, что Kf = const, Cp = const, αf = const – заданные параметры, завися- щие от точки пространства, но не зависящие от времени и состояния среды. В частном случае несжимаемой жидкости (Kf →∞, αf =0) и малых изменений температуры имеем ρf =ρ0f , Δsf=CpΔΘ/Θ0. Зависимости внутренней энергии от давления и температуры (уравнения состояния) могут быть получены непосредственно из уравнений (3).
С учетом условий малых изменений свойств насыщенной среды, можно показать, что
Δm=ρ0 v,v=B:ΔE+ Δp-3αΔΘ, (4) ffff M m где vf – относительное изменение объема жидкости в элементарном объеме насыщенной среды.
2. Геометрическая модель трещины
Толщина (раскрытие) трещины ГРП имеет среднюю величину порядка единиц миллиметров, максимальную – порядка единиц сантиметров. В то же время характерный размер области Ω , в которой решается задача (масштаб элемента системы заводнения), составляет десятки-сотни метров, характерная полудлина трещины – десятки-сотни метров, высота – до единиц-десятков метров. По этой причине не имеет смысла рассматривать трещину как трехмерный объект при изучении пороупругих процессов во вмещающей трещину среде. Поэтому при построении модели насыщенного напряженно-деформированного пласта будем считать трещину разрезом нулевой толщины, который соответствует срединной поверхности Г трещины. Срединной поверхностью назовем условную поверхность, равноудаленную от берегов трещины.
Будем считать, что срединная поверхность трещины является гладкой, односвязной поверхностью
Г : D Г ^ Ж 3 , D Г с Ж 2 , (5)
с краем д Г , который соответствует фронту трещины.
Обозначим через Г , рассматриваемую поверхность в момент времени t , при этом для t 1 ≥ t 2 выполняется условие Г , 1 с Г 2, .
В дальнейшем будем считать, что в каждый момент времени на линии у ( t ) = дГ( задано векторное поле скорости v = v ( x , t ), x ∈ γ ( t ), описывающее ее эволюцию. Таким образом, движение точки границы описывается уравнением
= v ( x , t ), x | t =0= x 0 ∈ γ (0), (6)
dt где поле скорости v=v(x,t) является гладкой функцией точки x ∈ γ(t) в каждый фиксированный момент времени t и гладкой функцией времени для каждой фиксированной (лагранжевой) точки границы.
3. Модель течения в трещине
Будем считать, что флюид распространяется по трещине с заданной геометрией, стремясь заполнить всю трещину. Таким образом, части трещины, занятой жидкостью, соответствует лишь часть срединной поверхности Т трещины. Раскрытие трещины является функцией точки поверхности Т , w = w ( x ), x e T . Относительно срединной поверхности будем предполагать, что ее кривизна мала.
Поверхность Т является срединной поверхностью трещины в том смысле, что боковые поверхности Т ± реальной, «физической» трещины находятся на расстоянии w /2 от срединной поверхности Т , Т ± = x + n ( x ) w ( x )/2, x e T . Здесь n ( x ) - нормаль к поверхности T в точке x , направленная в сторону Т - (таким образом, n + = n , n - = — n ). Естественными ограничениями на вид функции w является ее гладкость, неотрицательность и равенство нулю на крае д Т , w ( x ) > 0 , x e T , w ( x ) = 0, x e д Т .
В приближении смазочного слоя уравнение течения сжимаемой жидкости, связывающее раскрытие w и давление pf в трещине, имеет вид [5]
""" tw + V T ( р f w v Т ) = Q f , v т = — D ( V T Pf — Р f g Т ) , (7)
где v T - средняя по раскрытию трещины скорость течения флюида в трещине, коэффициент D является эффективной проницаемостью трещины и в общем случае определяется свойствами жидкости и состоянием среды; g т -проекция вектора ускорения свободного падения на срединную поверхность трещины, g т = ( I — n ® n ) g . В простейшем случае ньютоновской жидкости D = w 2 / (12 ц f ), где ц f - динамическая вязкость флюида.
В общем случае неньютоновской жидкости D = D ( w , V Tpj ) (см., например, [6]). Символом V Т обозначен поверхностный оператор Гамильтона [7].
Величина Q f в правой части уравнения (7) описывает мощность источников. Для трещины ГРП она может быть представлена в виде Q f = Q f + Q™ ' , где первое слагаемое описывает мощность потока флюида из скважины в трещину (и задается как точечный источник, мощность которого определяется параметрами закачки и моделью течения в скважине), второе - утечку флюида в пороупругий пласт (определяется условиями согласования, см. п. 4).
Уравнение (7) рассматривается в ограниченной области Qf = Qf (t) с Т , занятой флюидом. Границу области Qf (t) будем обозначать как cQf (t). Будем считать, что Qf - односвязная область, а dQf - замкнутая гладкая кривая (рис. 2). На границе dQf этой области должны быть заданы соответствующие граничные условия, которые будут рассмотрены в п. 5.
В ряде практически важных случаев уравнение (7) может быть дополнено уравнением, описывающим перенос флюидом в трещине того или иного пассивного компонента (например, «проппанта» - специального калиброванного «песка», предназначенного для того, чтобы трещина не «закрылась» в случае, если давление флюида в ней упадет достаточно сильно). Соответствующие модели широко известны (см., например, [6, 8]) и практически не меняют структуру рассматриваемой модели и вид ее уравнений. По этой причине здесь они не рассматриваются.
В общем случае эволюция фронта жидкости описывается так же, как и фронта трещины (см. п.п. 2 и 5).
В случае необходимости учета неизотермических эффектов при описании течения в трещине уравнения сохранения массы флюида дополняются уравнением сохранения энергии. В случае слабосжимаемой жидкости в трещине (трехмерное) уравнение закона сохранения энергии имеет вид (без учета внешних источников тепла)
' (р fe) + V (—X0V® + р fC 0 v т ) — D: T = 0, (8)
где p f A e = p f C A0 - объемная плотность внутренней энергии флюида; Х0 - коэффициент теплопроводности флюида; р f C - объемная теплоемкость флюида; D -тензор скоростей деформации. Последнее слагаемое в (8) описывает диссипацию энергии за счет работы вязких сил во флюиде.
Интегрирование уравнения (8) по толщине трещины в интервале от — w /2 до + w /2 дает
∂ д'(wpfC0Т ) + VT х х (—wХТ V Т 0Т + wp fC 0Т vT) — Р + q 0 =0,
где 0 Т - средняя по толщине трещины температура; Р - диссипация за счет работы вязких сил; q 0 - приток тепла через боковые поверхности трещины.
С учетом допущений о структуре течения в тонком смазочном слое (локально пуазейлевский профиль, малые числа Рейнольдса, малость толщины слоя) для величины диссипации Р может быть получено выражение Р = ( 12 ц Т ) / w v T . Для течений рассматриваемого класса эта величина обычно мала и ей можно пренебречь, то есть считать Р = 0 .
4. Условия согласования «вмещающая среда»/«трещина»
Величины, описывающие напряженно-деформированное и насыщенное состояние пласта (поле перемещений, тензоры напряжений и деформаций, давление флюида в пласте, скорость фильтрации) терпят при переходе через ее срединную поверхность Г скачок, величина которого определяется специальными условиями согласования. Эти условия связывают рассмотренные выше независимые группы уравнений, описывающие состояние пороупругой вмещающей среды и течение в трещине. Условия согласования включают в себя кинематические условия и условия, обеспечивающие непрерывность потоков импульса, массы и энергии. Рассмотрим их последовательно.
Пусть далее x е Г - точка на срединной поверхности трещины, х± - соответствующие ей (в смысле проекции кратчайшего расстояния) точки на боковых поверхностях («берегах») Г± трещины, n± - вектор единичной внешней нормали к вмещающей среде на боковых поверхностях трещины (рис. 1). Как и ранее (см. п. 3), считаем n+ = n, n- = -n, (10)
где n – единичная нормаль к срединной поверхности Г , направленная в сторону от Г + к Г - (см. рис. 1).
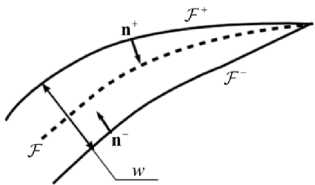
Рис. 1. Ориентация боковых поверхностей (берегов) трещины
Fig. 1. Orientation of lateral surfaces (shores) of the crack
К первой группе условий согласования относятся кинематические условия, связывающие перемещения берегов трещины и ее раскрытие. Эти условия имеют вид w (x) = (u+ - u-) ■ n = [u] ■ n = [ Un ], где u± = u*■ n; [un ] = u+- u-; u± = u(x±). В рассматриваемой постановке задачи нельзя сделать естественных априорных предположений о скачке тангенциальных компонент поля перемещений при переходе через поверхность Г : величина этого скачка неизвестна и определяется решением задачи.
Рассмотрим теперь динамические условия согласования, которые имеют вид условий непрерывности нормальной компоненты тензора напряжений на берегах трещины:
T
■ n = - p n , T ■ n = - p n , откуда с учетом (10) имеем
T+ ■ n = -p*n, T- ■ n = -p*n, где T± = T(x±).
Эти соотношения можно записать в эквивалентном виде как соотношения для скачка и среднего значения нормальных напряжений при переходе через срединную поверхность Г :
[ T ] ■ n = 0, { T } ■ n = - p * ■ n , (11) где (здесь и далее) [ a ] = a +- a - ; { a } = 1/2 ( a + + a - ) для какой-либо величины a . В последнем уравнении величина p * имеет смысл давления, приложенного к берегам трещины. Конкретный вид p * и его связь со значением давления во вмещающей среде и трещине будут рассмотрены ниже. Условия (11) предполагают, что силы вязкого трения, действующие на берега трещины со стороны заполняющего трещину флюида, пренебрежимо малы.
Рассмотрим теперь условия согласования для «гидродинамической» части задачи, включающей в себя уравнения фильтрации в пористой вмещающей трещину среде и уравнение течения непосредственно в трещине. Эти условия связывают давление в трещине, вмещающей среде и соответствующие потоки массы. Они будут иметь различный вид в зависимости от допущений, накладываемых на условия течения.
В первом случае будем считать, что трещина и вмещающая среда заполнены одним и тем же флюидом, который заполняет весь объем трещины, причем гидродинамический контакт между трещиной и вмещающей средой - идеальный. В этом случае в точке x е Г
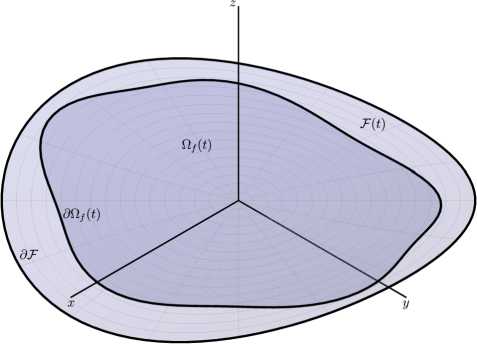
Рис. 2. Взаимное расположение срединной поверхности трещины и области, занятой флюидом Fig. 2. Relative position of fracture mid-surface and fluid domain срединной поверхности имеем p+ = p- = pf,
где, как и ранее, p ± = p ( x ± ), или, что эквивалентно [ p ]=0, { p } = pf .
Условия непрерывности потока массы с учетом соответствующих выражений для течения во вмещающей среде (2) и вида уравнения (7), выражающего закон сохранения массы в трещине, имеют вид
Qf = Q + + Q - , Q ± = wm • n ± l +. (13) f x = x_
Таким образом, величина потока из среды в трещину определяет правую часть закона сохранения массы флюида в трещине, а давление в трещине играет роль граничного условия для давления на берегах трещины.
В рассматриваемом случае естественно считать, что область срединной поверхности, соответствующая объему трещины, занятому флюидом, совпадает со всей срединной поверхностью, то есть Q f = У . При этом p * в (11) определено как p * ( x ) = pf ( x ).
Во втором случае будем считать, что флюид в трещине не проникает во вмещающую среду. Это может быть связано как механической изоляцией объема вмещающей среды, так и существенным отличием свойств флюида в трещине от флюида во вмещающей среде. В этом случае будем считать, что часть срединной поверхности, соответствующая объему, занятому флюидом, не совпадает со всей срединной поверхностью трещины, то есть Q f с У , dQ f ^д У = 0 (см. рис. 2).
Тогда условия согласования для потока массы флюида в области Q f имеют вид
Q f =0, Q ± =0, x eQ f . (14)
Другими словами, условия согласования вырождаются в граничные условия Неймана для уравнения фильтрации во вмещающей среде. В этом случае условия для давления во вмещающей среде не могут быть сформулированы, а давление в трещине определяется уравнением (7) c заданной (нулевой) правой частью Q f . Величина p * в (11) задается как p * ( x ) = p f ( x ).
Аналогичные условия согласования в области У \ Q f (области «лага») могут быть заданы по-разному в зависимости от того, являются ли берега трещины проницаемыми или нет для флюида во вмещающей среде. В первом случае в точках x e У \ Q f имеем Q ± =0 и p * ( x ) = 0 в (11). Во втором случае естественно считать, что в рассматриваемой области трещины, соответствующей части срединной поверхности У \ Q f , находится поровый флюид, давление которого непрерывно при переходе через берега трещины, то есть [ p ] = 0, [ Q ] = 0 .
Наконец, рассмотрим практически важный случай, когда флюид в трещине не проникает во вмещающую среду, но содержит в своем составе компонент, который может проникать во вмещающую среду. Тогда обычно считается, что потоки на берегах трещины определены как функции свойств флюида, фильтрационноемкостных свойств среды и полей давления в трещине и ее окрестности. В рамках рассматриваемой модели это приводит к условиям
Q f = Q + + Q " , Q ± = Q ± ( p f , p ± ) = w m • n" -
Последняя зависимость может быть задана, например, в соответствии с моделью утечки Картера или ее обобщений [9, 10].
Рассмотрим теперь баланс потока энергии. Будем считать, что в точках границы У± насыщенная пороупругая среда (скелет и флюид) и флюид в трещине находятся в состоянии локального теплового равновесия. В этом случае имеем 0± = 0У , или, эквивалентно, [0] = 0 , {0} = 0У . В случае если утечка массы из трещины во вмещающую среду не происходит, условия непрерывности потока энергии будут иметь вид q 0 = Q:+ Q-, Q0 = q^ n±.
При этом первое уравнение, по существу, является определением для мощности источников энергии в уравнении (9), а температура в трещине играет роль граничного условия для уравнения закона сохранения энергии в среде.
В том случае если утечка массы происходит и, так или иначе, задана значениями Q±, условия непрерывности потока энергии будут иметь вид q0 = Q+ + Q, Q0 = hQ± = (hfwm + q0 )|x=x± • n±.
Тогда заданным можно считать поток из трещины во вмещающую среду. Значение температуры при этом определятся полным решением задачи.
5. Граничные условия на фронте трещины
Под действием внешних нагрузок (объемных сил и «механических» граничных условий) и в процессе закачки флюида в трещину она может развиваться. С математической точки зрения это соответствует развитию срединной поверхности трещины. В дальнейшем будем считать, что развитие трещины происходит ква-зиравновесным образом. Это означает, что в любой момент времени среда находится в состоянии механического равновесия, которое определяет стационарное положение фронта трещины. Условия, определяющие рост трещины, по существу, являются уравнениями, определяющими положение фронта трещины в каждый конкретный момент времени.
Изучение условий развития трещин является предметом механики разрушения. Более полный обзор этих вопросов в настоящей работе не предусматривается, для знакомства с ними см., например, [11, 12].
В рамках настоящей работы будем считать, что разрушение среды является хрупким и рассматривается в рамках линейно-упругой модели среды. Для таких задач вопрос о возможности развития трещины обычно решается путем анализа значений коэффициентов интенсивности напряжений в точках фронта трещины. Коэффициенты интенсивности напряжений, в свою очередь, определяются как коэффициенты при главных сингулярных асимптотиках поля напряжений в окрестности точки фронта трещины. В общем случае можно определить три таких коэффициента, соответствующих трем режимам нагружения трещины (которые определяются относительной ориентацией касательным к фронту трещины вектором и направлением нагрузки, приложенной к берегам трещины).
Альтернативным подходом является использование энергетического критерия разрушения. В этом случае с элементом площади срединной поверхности трещины связывается некоторая энергия, необходимая для его образования. Соответственно, развитие поверхности трещины связано с потоком энергии, который относится к соответствующей точке фронта трещины. Формализация этого рассуждения приводит к понятию J -интеграла Черепанова-Райса [11]. В настоящей модели используется именно такой подход. При этом используется так называемая векторная форма J -интеграла [11]. Вариант векторного J -интеграла для задачи теории пороупругости рассмотрен в [13]. Конкретный вид и способ вычисления векторного J -интеграла в настоящей работе не рассматривается. Укажем лишь его «функциональную» форму, достаточную для замыкания уравнений рассматриваемой модели.
А именно, в соответствии с [13] будем считать, что при заданном положении фронта д у трещины в момент времени t в каждой его точке x е дГ, можно определить вектор J = J ( x ). С физической точки зрения вектор J определяет количество энергии J , высвобождаемой при локальном развитии трещины в заданном направлении l (|| l ||= 1 ), J = J ⋅ l . В соответствии с энергетическим критерием развития трещины ее рост происходит в направлении вектора l , при котором величина высвобождаемой энергии максимальна, J = J max = J ( l max). В случае если J max ≤ J *, где J * – некоторое критическое значение энергии, которое обычно считают свойством материала, роста трещины не происходит. При J max = J * происходит устойчивый рост трещины, при J max > J * – неустойчивый.
Таким образом, если рост трещины в заданной точке происходит, локальное направление роста совпадает с направлением вектора J , то есть в уравнении (6) имеем v = α J , α≥ 0 .
Вместе с тем теория квазиравновесной трещины в упругой среде не позволяет непосредственно определить скорость развития трещины, то есть значение коэффициента α в случае, если он положителен. Поэтому уравнение (6) является «кинематическим», то есть дает удобную параметризацию поверхности трещины. Оно должно быть дополнено непосредственно уравнением для определения положения фронта трещины, которое уже было сформулировано выше и имеет вид Jmax ≤ J* . Это уравнение является нелокальным и зависит от ис- тории развития трещины, текущей формы ее поверхности, решения задачи пороупругости во всей области и распределения давления внутри трещины.
В совокупности приведенные уравнения означают, что в ходе развития трещины в каждой точке ее фронта вектор, касательный к поверхности трещины и нормальный к ее фронту, соосен вектору J в заданной точке, при этом в этой точке выполняется соотношение J ≤ J . При этом α =0 в точках, где J < J . max max
В точках, где происходит рост трещины, справедливо уравнение J max = J * . Это условие, по существу, является уравнением относительно параметра α , который определяет скорость, с которой точка фронта трещины «продвигается» в направлении вектора J .
Приведенные выше рассуждения касаются исключительно вопроса о развитии трещины с точки зрения модели поведения вмещающей среды. Рассмотрим теперь случай трещины, заполненной флюидом.
Будем считать сначала, что область, заполненная флюидом, «меньше», чем область трещины. Другими словами, в любой момент времени t имеем Q f ( t ) с У и dQ f ( t ) п дУ = 0 . Это условие предполагает (если не указано обратное), что в каждой точке фронта раскрытие положительно, то есть w ( x ) ≥ w 0 >0, x ∈ Γ ( t ). В этом случае флюид в трещине «растекается» по уже существующей трещине, пытаясь заполнить весь ее объем. Часть Ω f срединной поверхности, соответствующая области трещины, занятой флюидом, в общем случае изменяется за счет притока флюида в трещину и изменения раскрытия трещины за счет деформации вмещающей среды.
Пусть n – единичная внешняя нормаль к ∂Ω f , касательная к срединной поверхности трещины, V – скорость движения границы Γ ( t )= ∂Ω f ( t ), w – как и ранее, раскрытие трещины, v y - средняя по раскрытию скорость движения частиц жидкости, ρ f – плотность жидкости, Qf – мощность массового источника жидкости, q f = Q f / ρ f – мощность объемного источника.
Интегрируя уравнение (7) по области, занятой флюидом, имеем
∂ρ f w
∫ ds + ∫ ρ fwvnd γ =
Ω f ( t ) ∂ t Γ( t )
= J Q f ds , v n = v y • n|Г( t ) . (15) Ω f ( t )
Это уравнение будет справедливо, если поток массы через границу области флюида связан исключительно с движением границы, то есть отсутствуют потоки массы, связанные с испарением через фронт флюида и так далее, и источник в правой части не является сингулярным на фронте. В таком случае нормальная компонента скорости распространения фронта жидкости Vn совпадает с нормальной компонентной vn средней скорости движения частиц жидкости на фронте.
dx f limvn=Vn= ⋅n, xf∈Γ(t). (16) x→xf dt
Несмотря на свою очевидность, соотношение (16) носит фундаментальный характер и связывает скорость движения точек границы со скоростью жидкости. Его называют уравнением для скорости фронта («speed equation») [14] или условием Стефана («Stefan condition») [15]. Как правило, на фронте тангенциальная компонента v τ частиц жидкости мала по сравнению с vn . В таком случае V = v , то есть скорости фронта и частиц жидкости совпадают (в общем случае это касается лишь их нормальных компонент).
В терминах потока уравнение для скорости (16) можно записать в виде q q⋅n
V n = lim — = lim ——, x f е Г ( t ); q ^ = p f W v r . (17) x → x f w x → x f ρ fw
Отметим, что уравнения (16) и (17) верны и в том случае, если на фронте жидкости раскрытие равно нулю (именно поэтому в этих уравнениях используется обозначение x → x f , а не x = x f ).
Теперь перейдем к обсуждению возможных граничных условий, которые могут быть наложены на уравнение (7) с учетом (16) и (17).
Первый вариант предполагает задание на фронте жидкости граничного условия (Дирихле) для давления, pf(x) =p*f(x), x ∈Γ(t), где p*f – заданная функция. Скорость движения фронта жидкости в этом случае определяется уравнением (17). Эволюция области, занятой флюидом, определяется уравнением, аналогичным (6), где скорость определяется уравнением (17). Значение p*f в точке фронта можно положить равным нулю в том случае, если пластовый флюид не проникает в область трещины, не занятую жидкостью, и p(xf ), если область «лага» заполнена пластовым флюидом.
Во втором варианте предполагается задание в каждой точке границы фронта флюида значения скорости движения точки фронта, или, что эквивалентно в силу (17), потока массы на фронте. Эволюция фронта трещины определяется указанным выше способом. При этом значение скорости движения фронта не может быть задано произвольно – она должна быть согласована с потоком массы в трещине и текущим значением раскрытия трещины соотношением (15).
Отметим, что в рассматриваемом случае естественным является первый способ задания граничных условий. При этом в задаче присутствуют два фронта – трещины и флюида, эволюция которых определяется независимо.
Наконец, рассмотрим случай, когда флюид может заполнять весь объем трещины. С математической точки зрения этот случай является наиболее сложным. Это связано с тем, что в точках фронта трещины раскрытие равно нулю, и поток в уравнении (7) формально вырождается. Однако в силу того, что фронт трещины и совпадающий с ним фронт флюида распространяются с конечной скоростью, скорость флюида на фронте, определенная в соответствии с (17), конечна. В силу этого значение давления в точках фронта имеет особенность и является неограниченным. Корректная постановка граничных условий для уравнения течения в трещине в этом случае является нетривиальной задачей. «Естественным» граничным условием в этом случае является задание скорости движения фронта, которая, в свою очередь, определяется решением задачи о развитии трещины. При этом содержательным становится использование соотношения (17), которое в данном случае рассматривается не как определение скорости движения фронта, а как уравнение, связывающее скорость движения фронта флюида и трещины. Различные способы корректной постановки граничных условий в этом случае рассмотрены, например, в [14, 15].
Сингулярность поля давления в трещине может быть устранена допущением о том, что в ходе развития трещины фронт флюида всегда немного отстает от фронта трещины на заданную величину. В этом случае говорят, что рассматривается модель трещины с «лагом». Величина лага заранее неизвестна. В общем случае она может быть определена рассмотрением постановки задачи с одновременным учетом эволюции двух фронтов – флюида и трещины.
Вместе с тем известно, что а) для практических расчетов важно существование лага как такового, а не его конкретная величина и б) учет лага существенен только на первоначальном этапе развития трещины ГРП (в дальнейшем величина лага становится несущественной и ей можно пренебречь). Поэтому зачастую величина лага определяется из тех или иных дополнительных соображений (см., например [16–18]) или считается малой фиксированной величиной.
6. Алгоритмические аспекты реализации модели
Описанная в предыдущих разделах математическая модель мало пригодна для теоретического анализа процесса развития трещины в силу своей сложности. Ее основное назначение – использование в виде математической модели для анализа средствами математического моделирования и вычислительного эксперимента. По этой причине ниже кратко представлены базовые алгоритмы вычислительной математики, которые могут быть использованы для реализации модели в описанном выше виде. Наличие таких методов, вообще говоря, обосновывает сложность модели и демонстрирует возможность ее реализации на практике.
Для решения уравнений, описывающих состояние вмещающей среды, то есть уравнений пороупругости, в настоящее время предложено значительное количество подходов. Последние включают в себя метод конечных разностей, метод конечных элементов и метод граничных интегральных уравнений. В силу того что модель предполагает произвольное пространственное распределение свойств вмещающей среды, наиболее приемлемым из указанных является метод конечных элементов [19]. Для аппроксимаций по времени чаще всего используются полностью неявные схемы (например, неявный метод Эйлера). Для решения конечномерной задачи могут использоваться как «монолитные» постановки (в рамках которых одновременно определяется как поле перемещений, так и поле давления), так и методы на основе итераций между группами уравнений упругости и фильтрации [20].
Характерным свойством системы уравнений поро-упругости в рассматриваемом приближении является то, что после аппроксимации по времени она имеет вид задачи о седловой точке [21]. В этом случае для устойчивости решения как континуальной, так и конечномерной задач необходимо выполнение так называемых inf-sup условий (условий Ладыженской–Бабушки– Бреззи) [21]. При нарушении этих условий в задачах пороупругости могут возникать численные неустойчивости конечномерного решения, особенно в предельном случае несжимаемой жидкости). Простейшим примером конечного элемента, удовлетворяющего этим условиям, является элемент Тэйлора–Худа, в котором для аппроксимации перемещений используются конечные элементы второго порядка, а для аппроксимации давления – первого [22–24]. Альтернативным подходом является регуляризация исходной задачи (см., например, [25– 27]). В случае если для конкретной задачи inf-sup устойчивые пары пространств неизвестны, необходим контроль за особенностями решения и проверка выполнения численных inf-sup условий [28].
Наличие в постановке задачи трещины приводит к тому, что решение связанной задачи термопороупруго-сти терпит разрыв при переходе через ее срединную поверхность. При этом компоненты полей перемещений, тензора деформаций и напряжений терпят сильный разрыв; поля давления и температуры являются непрерывными, соответствующие потоки (массы флюида и энергии) терпят, вообще говоря, сильный разрыв. В рамках традиционных подходов считается, что разрыв проходит по ребрам и/или граням сетки. Использование таких подходов требует применения дорогостоящих процедур перестройки расчетной сетки на каждом шаге развития трещины и корректной (консервативной) интерполяции расчетных величин со «старой» сетки на «новую».
Более оправданным является использование методов, предполагающих подсеточное разрешение трещины. В методах этого класса считается, что геометрия срединной поверхности трещины не согласована с геометрией сетки во вмещающем трещину пространстве. Для учета разрыва решения в ячейках сетки, через которые проходит трещина, используются специальные базисные функции, допускающие наличие сильного или слабого разрыва конечномерного решения внутри этих ячеек. К методам этого класса относятся методы типа Assumed Strain Elements [29, 30], X-FEM (eXtended Finite Elements), метод Нитше (Nitsche method) и др. При использовании методов этого класса перестройка сетки не является необходимой для корректного описания развития трещины процедурой: если она и проводится, то с целью повышения фактической точности решения. Отметим, что в контексте метода X-FEM обычно используется неявное представление срединной поверхности трещины, когда она описывается как поверхность уровня ноль заданной в объеме функции. Для описания эволюции таких поверхностей разработан целый ряд эффективных методов на основе решений уравнений типа Гамильтона-Якоби (см., например, [31, 32]).
В случае если срединная поверхность трещины не согласована с геометрией расчетной сетки во вмещающей среде, возникает вопрос о конечномерной аппроксимации условий согласования на границе «трещина– пласт». В частности, условия равенства двух функций, определенных в объеме и на срединной поверхности, не могут быть выполнены поточечно. В этом случае стандартным способом является аппроксимация условий равенства в слабом (в смысле вариационной постановки задачи) смысле. Типичными примерами таких подходов являются методы штрафа, классический и регуляризованный метод множителей Лагранжа и метод Нитше.
Построение inf-sup устойчивых пространств для множителей Лагранжа для конечно-элементных аппроксимаций метода X-FEM рассмотрено в работах [33–36]. Метод Нитше изначально был предложен в работе [37] и в дальнейшем развит, в том числе в контексте метода X-FEM в работе [38].
Наконец, рассмотрим вопросы, связанные с решением уравнения смазочного слоя, определенного на срединной поверхности трещины. В том случае, если срединная поверхность трещины образована гранями расчетной сетки во вмещающей среде, решение этой задачи не представляет принципиальных проблем (см., например, [39] и ссылки там). В том случае, если поверхность трещины не согласованна с сеткой, а сама поверхность задана неявно, задача становится значительно сложнее. Можно выделить целый ряд методов, разработанных для ее решения.
В первом классе методов (условно – «методы на основе погружения поверхности») поверхность, на которой решается уравнение, считается погруженной в трехмерное пространство. Геометрия поверхности задается неявно, как поверхность уровня ноль заданной функции, определенной в трехмерном пространстве. Суть метода заключается в том, что заданное на поверхности уровня ноль уравнение продолжается во все пространство (то есть на все поверхности уровня) так, что решение этого уравнения совпадает с решением исходного уравнения на поверхности. Далее «продолженное» уравнение аппроксимируется во всей трехмерной области «стандартным» методом конечных элементов. След трехмерного решения на исходной поверхности дает решение исходной задачи. Метод этого типа изначально был предложен в [40, 41].
Второй класс методов относится к классу методов типа «диффузной границы», «diffuse interface approach» [42]. Этот класс методов близок к рассмотренному ранее. Общая идея сохраняется, однако способ продолжения уравнения на поверхности в трехмерное пространство отличается от рассмотренного ранее. Метод основан на том, что коэффициенты уравнения рассматриваются как пространственные обобщенные дельта-функции (меры Дирака) с носителем на поверхности. Замена этих распределений на сходящиеся к ним элементы дельтаобразных последовательностей позволяет построить задачу во вмещающей среде, след которой сходится к решению задачи на поверхности.
Еще один подход рассмотрен в работе ([43], см. также ссылки там). В соответствии с ним уравнение на поверхности не модифицируется, но для аппроксимации его решения используются конечно-элементные базисные функции, заданные на трехмерной сетке во вмещающей среде.
Наконец, удобной альтернативой указанным классам методов можно считать метод на основе проекции ближайшей точки, предложенный в [44]. Его принципиальной особенностью является способ описания поверхности, который естественно позволяет рассматривать поверхности с краем.
Список литературы Математическая модель развития трещины гидроразрыва пласта в трехмерной пороупругой среде
- Гидравлический разрыв карбонатных пластов/В.Г. Салимов, Н.Г. Ибрагимов, А.В. Насыбуллин, О.В. Салимов. -М.: Нефтяное хозяйство, 2013. -471 c.
- Экономидес М., Олини Р., Валько П. Унифицированный дизайн гидроразрыва пласта. От теории к практике/Институт компьютерных исследований. -М., 2007. -236 c.
- Michael J. Economides, Kenneth G. Nolte (Eds.) Reservoir Stimulation. -Wiley, 2000. -856 p.
- Coussy O. Poromechanics, John Wiley and Sons, 2004.
- Chipot M., Luskin M. The compressible Reynolds lubrication equation//IMA Preprint Series. -1986. -No. 232.
- Computer simulation of hydraulic fractures/J. Adachi, E. Siebrits, A. Peirce, J. Desroches//Int. J. Rock Mech. Min. Sci. -2007. -Vol. 44. -P. 739-757.
- Дубровин Б.А., Новиков С.П., Фоменко А.Т. Современная геометрия. Методы и приложения. -М.: Наука, 1986. -760 c.
- Eskin D., Miller M.J. A model of non-Newtonian slurry flow in a fracture//Powder Technology. -2008. -Vol. 182. -P. 313-322.
- Clifton R.J., Wang J.-J. Multiple fluids, proppant transport, and thermal effects in threedimensional simulation of hydraulic fracturing//SPE Paper. -1988. -18198.
- Clifton R.J., Brown U., Wang J.-J. Modeling of Poroelastic Effects in Hydraulic Fracturing//SPE Paper. -1991. -21871.
- Черепанов Г.П. Механика хрупкого разрушения. -М.: Наука, 1974. -640 с.
- Качанов Л.М. Основы механики разрушения. -М.: Наука, 1974. -312 с.
- Рамазанов М.М., Критский Б.В., Савенков Е.Б. Формулировка J-интеграла для модели пороупругой среды Био//ИФЖ. -2018. -T. 91, № 6.
- Линьков А.М. Уравнение скорости и его применение для решения некорректных задач о гидроразрыве//Докл. Акад. наук. -2011. -Т. 439, № 4. -С. 473-475.
- Detournay E., Peirce A. On the moving boundary conditions for a hydraulic fracture//International Journal of Engineering Science. -2014. -Vol. 84. -P. 147-155.
- Garagash D.I., Detournay E. The tip region of a fluid-driven fracture in an elastic medium//ASME J. Appl. Mech. -2000. -Vol. 67. -No. 1. -P. 183-192.
- Garagash D.I. Propagation of a plane-strain fluid-driven fracture with a fluid lag: early-time solution//Int J Solids Struct. -2006. -Vol. 43. -P. 5811-5835.
- Linkov A.M. Particle velocity, speed equation and universal asymptotics for efficient modelling of hydraulic fracturing//Journal of Applied Mathematics and Mechanics. -2015. -Vol. 79. -No. 1. -P. 54-63.
- Lewis R.W., Schrefler B.A. The Finite Element Method in the Static and Dynamic Deformation and Consolidation in Porous Media. -J. Wiley, Chichester, 1998.
- Kim J., Tchelepi H.A., Juanes R. Stability, Accuracy and Efficiency of Sequential Methods for Coupled Flow and Geomechanics//SPE Paper. -2009. -119084.
- Brezzi F., Fortin M. Mixed and Hybrid Finite Elements Methods. -Springer, 1991.
- Ern A., Meunier S. A-posteriori error analysis of Euler-Galerkin approximations to coupled elliptic-parabolic problems//ESAIM: M2AN. -2009. -Vol. 43. -No. 2. -P. 353-375.
- Murad M.A., Thomee V., Loula A.F.D. Asymptotic Behavior of Semidiscrete Finite-Element Approximations of Biot’s Consolidation Problem//SIAM Journal on Numerical Analysis. -1996. -Vol. 33. -No. 3. -P. 1065-1083.
- Showalter R.E. Diffusion in Poro-Elastic Media//Journal of Mathematical Analysis and Applications. -2000. -Vol. 251. -No. 1. -P. 310-340.
- White J.A., Borja R.I. Stabilized low-order finite elements for coupled solid-deformation/fluid-diffusion and their application to fault zone transients//Comput. Methods Appl. Mech. Engrg. -2008. -Vol. 197. -No. 49-50. -P. 4353-4366.
- Commend S., Truty A., Zimmermann Th. Stabilized finite elements applied to elastoplasticity: I. Mixed displacement-pressure formulation//Comput. Methods Appl. Mech. Engrg. -2004. -Vol. 193. -P. 3559-3586.
- Xia K., Masud A.A stabilized finite element formulation for finite deformation elastoplasticity in geomechanics//Computers and Geotechnics. -2009. -Vol. 36. -P. 396-405.
- Chappele D., Bathe K.J. The inf-Test//Computers & Structures. -1993. -Vol. 47. -No. 4-5. -P. 537-545.
- Simo J.C., Rifai M.S. A class of mixed assumed strain methods and the method of incompatible modes//Int. J. Numer. Methods Engrg. -1990. -Vol. 29. -P. 1595-1638.
- Oliver J., Cervera M., Manzoli O. Strong discontinuities and continuum plasticity models: the strong discontinuity approach//Int. J. Plasticity. -1999. -Vol. 15. -P. 319-351.
- A PDE-based fast local level set method/D. Peng, B. Merriman, S. Osher, H. Zhao, M. Kang//Journal of Computational Physics. -1999. -Vol. 155. -P. 410-438.
- Chopp D.L. Computing minimal surfaces via level-set curvature flow//Journal of Computational Physics. -1993. -Vol. 106. -P. 77-91.
- Mourad H.M., Dolbow J., Harari I. A bubble-stabilized finite element method for Dirichlet constraints on embedded interfaces//International Journal for Numerical Methods in Engineering. -2007. -Vol. 69. -No. 4. -P. 772-793.
- Dolbow J.E, Franca L.P. Residual-free bubbles for embedded Dirichlet problems//Computer Methods in Applied Mechanics and Engineering. -2008. -Vol. 197. -P. 3751-3759.
- Bechet E., Moës N., Wohlmuth B. A stable Lagrange multiplier space for stiff interface conditions within the extended finite element method//Int. J. Numer. Meth. Engng. -2009. -Vol. 78. -P. 931-954.
- Hautefeuille M., Annavarapu C., Dolbow, J.E. Robust imposition of Dirichlet boundary conditions on embedded surfaces//Int. J. Numer. Meth. Engng. -2012. -Vol. 90. -P. 40-64.
- Nitsche J. Uber ein Variationsprinzip zur Losung von Dirichlet-Problemen bei Verwendung von Teilrümen, die keinen Randbedingungen unterworafen sind//Abh. Math. Sem. Univ. Hamburg. -1971. -Vol. 36. -P. 9-15.
- Dolbow J., Harari I. An efficient finite element method for embedded interface problems//International Journal for Numerical Methods in Engineering. -2009. -Vol. 78. -No. 2. -P. 229-252.
- Dziuk G., Elliott C.M. Surface finite elements for parabolic equations//J. Comput. Math. -2007. -Vol. 25. -P. 385-407.
- Variational problems and partial differential equations on implicit surfaces/M. Bertalmio, L.T. Cheng, S. Osher, G. Sapiro//J. Comput. Phys. -2001. -Vol. 174. -P. 759-780.
- Dziuk G., Elliott C.M. An Eulerian approach to transport and diffusion on evolving implicit surfaces//Comput Visual Sci. -2010. -Vol. 13. -P. 17-28.
- Ratz A., Voigt A. PDEs on Surfaces: A Diffuse Interface Approach//Comm. Math.Sci. -2006. -Vol. 4. -No. 3. -P. 575-590.
- Olshanskii M.A., Reusken A., Xu X. A Volume Mesh Finite Element Method for PDEs on Surfaces//European Congress on Computational Methods in Applied Sciences and Engineering (ECCOMAS 2012), eds. J. Eberhardsteiner et.al. -Vienna, Austria, September 2012. -Р. 10-14.
- Ruuth S.J., Merriman B. A simple embedding method for solving partial differential equations on surfaces//Journal of Computational Physics. -2008. -Vol. 227. -P. 1943-1961.


