Математическая модель роста ВВП

Анализ развития экономики страны включает множество показателей. Выбор набора характеристик определяется конкретными задачами и целями. В эти показатели входят численность населения, количество пенсионеров, денежные доходы, ВВП, инвестиции, ввод фондов, денежная масса и др. [1]. Статистические данные ежегодно сообщаются статистическими органами РФ [2]. Основным показателями, по которому ориентируются специалисты, является ВВП. Рост ВВП рассматривается как положительный фактор, а уменьшение - как спад производства. Для поддержания производства и его развития необходимы новые производственные фонды и инвестиции в производство, науку, образование [3].

Рост ВВП обеспечивается ресурсами, вкладываемыми в развитие экономики. Используются различные механизмы привлечения средств в модернизацию производства. Рост

ВВП сопровождается ростом доходов, улучшением качества жизни населения [4]. Свободные финансовые средства населения можно направить на потребление или сбережение. Простое сбережение изымает средства из оборота и создаёт предпосылки для кризисов. Инвестирование же вовлекает сбережения в оборот.

Экономическое развитие страны после кризисного периода с 1990 г. по 1999 г. приняло устойчивый характер после 2000 года [1]. С учетом этого все показатели за 2000 год приняты за единицу измерения. Расчет производится в рублях. Статистические показатели – рост ВВП, основных фондов и вкладов населения отражены на рисунке 1. Символом «*» отмечены статистические данные. Темпы рост инвестиций и ВВП отличаются не более чем на 5% в рассматриваемом временном интервале.

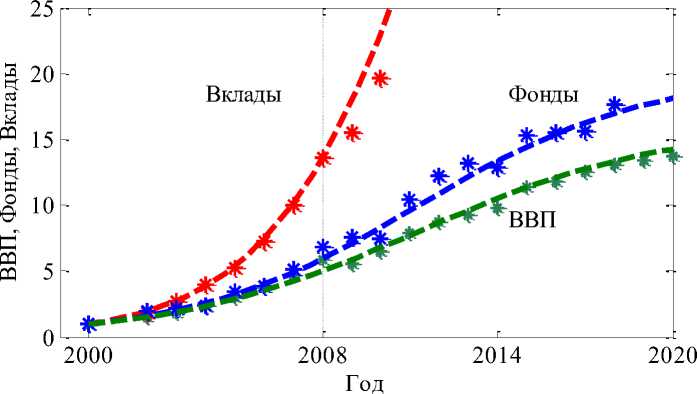
Рис. 1. Динамика роста ВВП, основных фондов, вкладов населения.

Основные показатели экономики изменялись с 2000 по 2008 годы по экспоненциальной зависимости [5]. После финансового кризиса 2008 г. скорость роста уменьшилась. На интервале с 2000 г. по 2021 г. статистические dy

dt

где Д - характеризует текущую удельную скорость роста, а K – предельное значение показателя, которое может быть достигнуто в рамках существующей системы экономических взаимоотношений. На рисунке 1 этим зависимостям отвечают пунктирные линии.

Значения параметров Д и K для основных экономических показателей среднемесячные доходы населения, доходы бюджета, ввод основных фондов, инвестиции, ВВП, душевого ВВП, денежной массы, пенсий, внутренней торговли и др. лежат в диапазоне от 0.20 до 0.25. Удельная скорость роста вкладов достигает 0.40. Параметр K лежит в диапазон от 17 до 25, а для вкладов – около 70, предельна емкость вкладов в 3-4 раза выше, чем у остальных показателей.

Проведенный анализ основных экономических показателей (рис. 1) показал, что в экономике происходит медленное уменьшение скорости роста абсолютных значений всех показателей. Единственный постоянно растущий показатель – накопление сбережений населения. В уравнении (1) параметр Д ха- данные в первом приближении описываются не экспоненциальной [6], а логистической зависимостью [7], являющейся решением уравнения.

y

У = д у ^{1 -} У

рактеризует текущую скорость роста материальных накоплений, а параметр K – предельное значение материального ресурса, которое может быть достигнуто при существующих экономических отношениях. Неизменность этого параметра и является основным фактором, приводящим для модели (1) к замедлению роста всех показателей.

Изменить предельные значения можно за счет изменений технологий производства, совершенствования систем управления, перераспределения материальных ресурсов и другими способами. Увеличение ВВП и инвестиций можно осуществить за счет уменьшения скорости накопления сбережений. То есть часть сбережений населения направить на модернизацию производства (ВВП) и вложение ресурсов в разработку новых технологий. То есть в модели (1) это увеличение параметра K .

Модель динамики трех показателей ВВП ( y ), накопления ( y ), инвестиции ( y ) с учетом (1) принимает вид.

dy^           1

У 1

—1 = Д1У1 1 - dt

dy

dy     1-^ С

1 г 2 У 2 ¹       ^2 ,

dt

dy3 dt

Д з У 3 ¹ -

У 3

где Д удельные скорости роста показателя, а K предельные значения на текущий момент ( i = 1,2,3 ). Под К₂ во втором уравнении понимается максимальная часть накоплений, которая может использоваться для изменения ВВП и инвестиций.

Функции C = C ( у ₂) определяют перераспределение части финансовых накоплений на увеличение предельных значений ВВП и инвестиций. За эти функции принимаются гиперболические зависимости.

C = а i    bi

+ У 2/ K 2

+ У 2 / K ₂

где параметры а_{ и b такие, что a_i >  b . При этом условии будут выполняться неравенства C >  1 . При этих ограничениях на параметры а и b функции C = C ( у₂ ) будут убывающими функциями своего аргумента.

То есть в модели (2) принимается, что значения K (ВВП) и K (инвестиции) увеличиваются за счет уменьшения K (предельного значения сбережений). То есть предельное значение ВВП увеличивается в C раз, предельное значений инвестиций в C раз, а предельное значение сбережений уменьшается в C раз.

Стационарная точка системы уравнений (2) находится из системы уравнений.

У 1 ₌ а 1 + у ₂ / K ₂ K 1    ^Ь 1 ⁺ У 2 / ^K 2 ,

^У 2 _ ^Ь 2 ^{+ У} 2 / K 2

К2 а2 + y2 / К2

У 3 ₌ а 3 + у 2 / K 2

к 3   b 3 + У 2 / K 2

Второе уравнение в (3) приводится к квадратному уравнению

Л2

У 2

+ ( а 2 - 1) ^ - b2 = 0 .

K 2

Это уравнение имеет корни противоположных знаков. При -У 2- = 0 левая часть

K 2

уравнения (4) принимает отрицательное зна- y чение, а при ---= 1 положительное, по-

K 2

скольку a ₂ >  b ₂ Поэтому система уравнений (3) имеет решение такое, что в новом устойчивом положении равновесия y ₂<  К ₂, а y₁ >  K и y ₃ >  K . То есть новое предельное значение сбережений уменьшится. А из первого и третьего уравнения в (4) следует, что предельные значения y и y . увеличатся.

На рис. 2 для случая a = 3.5 , a ₂ = 1.5 , a ₃ = 2.2 , b = b ₂ = b ₃ = 1 приведена динамика показателей (ВВП, инвестиции и вклады), если перераспределение сбережений начинается в 2022 году. Пунктирные линии соответствуют «планируемому» на основе модели (2) росту ВВП и инвестиций, а вертикальной пунктирной линией отмечен год начала перераспределения ресурсов. Сбережения к 2040 г. уменьшились в 3 раза, ВВП увеличился в 4

раза, а инвестиции – в 2 раза по сравнению с 2020 годом. Восстановление сбережений за счет роста ВВП и инвестиций не учитывается.

Имитационное моделирование распределения вероятностей ВВП и инвестиций осуществляется случайным выбором параметров a. и b_i ( i = 1,2,3 ) из заданного диапазона [7]. За начальные данные принимаются данные за 2021 г. Расчетное распределение вероятностей этих показателей на 2040 г. приведено на рисунке 3. Вертикальными пунктирными линиями отмечены медианы распределений. Модель (2) учитывает только перераспределение ресурсов направляемых на увеличение предельных значений ВВП и инвестиций. Удельные скорости роста в этой модели не изменяются. Текущие показатели будут увеличиваться с большей скоростью, но темпы роста будут уменьшаться – медленная стагнация остается. То есть перераспределение текущих ресурсов может дать положительный эффект на коротком временном интервале [8]. Результаты математического моделирования могут быть использованы на стадии принятия управленческих решений [9, 10].

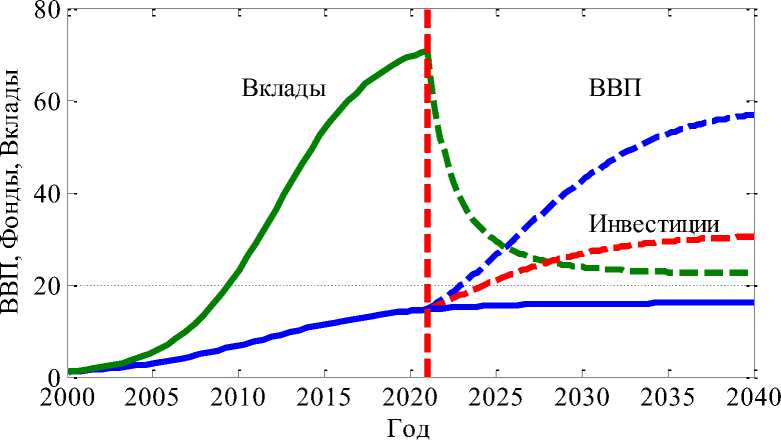
Рис. 2. Динамика показателей до 2022 года и после 2022 года (пунктирные линии)

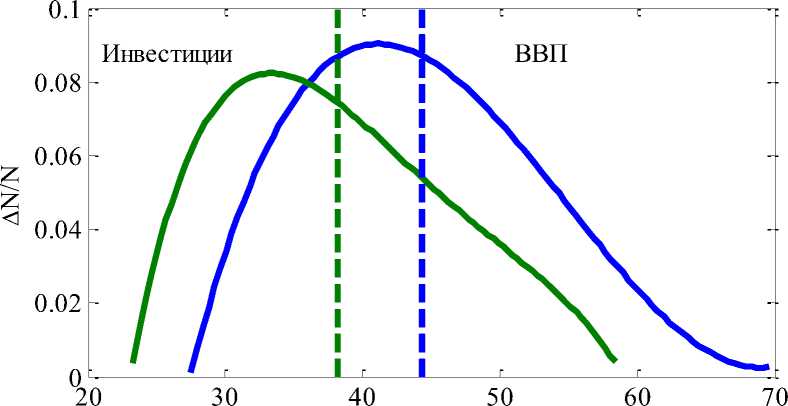
ВВП, Инвестиции (2030 г.)

Рис. 3. Вероятность распределения роста бюджета и инвестиций на 2030 г.

Разработанная математическая модель учитывает только перераспределение ресурсов направляемых на увеличение предельных значений ВВП и инвестиций. Удельные скорости роста в этой модели не изменяются. Текущие показатели будут увеличиваться с большей скоростью, но темпы роста будут уменьшаться – медленная стагнация остается. То есть перераспределение текущих ресурсов может дать положительный эффект на коротком временном интервале. Для постоянного увеличения темпов роста необходимо, как один из вариантов, изменение технологий производства, возвращение в оборот уже использованных ресурсов, дополнительное освоение природных ресурсов и развитие интеллектуального потенциала общества.