Математическая модель щеточного уплотнения

ход уплотняемой среды, достаточный для отвода тепла. Щеточные уплотнения через короткое время приработки имеют глянцевую рабочую поверхность, работающую как самогенерируе-мый подшипник. При этом утечки через пористую среду значительно выше, чем через зону контакта. Допустимая величина контактной силы с точки зрения ресурса (изнашивания) подбирается опытным путем. К сожалению, практически полностью отсутствуют публикации о методах расчета щеточных уплотнений.

При создании щеточных уплотнений ротора требуется решение следующих задач: отработка конструкции и технологии изготовления щетки; исследование газодинамических свойств уплотнений; исследование теплового состояния и фрикционных свойств упругого элемента; исследование упругодемпфирующих свойств элементов уплотнений.

Для создания методики проектирования щеточных уплотнений ротора необходима методика их теплового расчетов. При решении некоторых из вышеперечисленных задач можно воспользоваться результатами исследований, представленных в работах [3, 4]. Гидравлические характеристики щеточных уплотнений можно определить, используя гидродинамическую модель материала МР, предложенную А.И. Белоусовым [5]. В этом случае расход газа через щеточное уплотнение можно определять по следующим формулам:

m

2 d п ² р П ³ F п ρ Δ p 153 µδ ЩЕТ (1 - П )²

– ламинарный

режим течения;

• m ^. = F _п   ^,         ρ p – турбулент-

• п       П3dпр

ный режим течения, где П – пористость; dпр – диаметр проволоки; δЩЕТ – ширина щетки; Fп – площадь выход- ного сечения щетки; р - плотность газа; Ц -динамическая вязкость газа; Aр - перепад давления газа.

Приведенные зависимости были экспериментально подтверждены для различных типов уплотнений [6].

Величину плотности (пористости) щетки при конструировании щеточного уплотнения приходится выбирать исходя из компромисса между герметичностью и надежностью. Щетка должна быть достаточно плотной, чтобы утечки были как можно меньше. Однако в этом случае возрастает выделяющееся в зоне трения тепло и ухудшается теплоотвод. Т.е., проволочки могут расплавиться или сгореть. Поэтому необходимо проведение теплового расчета щеточного уплотнения. При этом могут быть использованы известные методики для расчета различных устройств [7, 8]. В частности, отвод тепла через проволочки из зоны трения и теплоотдача протекающему через уплотнение воздуху аналогичны эффекту оребрения камер сгорания жидкостных ракетных двигателей или интенсификации охлаждения лопаток турбин газотурбинных двигателей путем применения штырьков.

Усиление теплоотдачи в охлаждающий газ учитывается коэффициентом эффективности оребрения П р , определяемым из соотношения [8]

ki =

4 + Bi

– коэффициент, учитывающий

неравномерность температуры по площади профиля проволочки;

Di _ аПР ГПР

Bi =   "    - число Био;

X

r _ПР , l - радиус и длина проволоки; F _ПР -площадь сечения проволоки; T _K - температура в зоне контакта; T _Г - температура газа.

Подставляя (2) в (1), получаем с учетом угла установки проволочек, принимаемым равным 450 /2/

Пр =1 -

nПРFПР

-

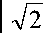
P nP r nP^{l a} r

17

Учет теплоотвода в корпус щеточного уплотнения можно оценить подобно учету теплоотвода наружной стенки в камерах ЖРД /8/. Он оценивается через коэффициент Z p •

^P 1 + ^^th ( p h э )th ( P l ) -

Р э

q г . р . = q гПр, где qГ.Р. , qГ - тепловые потоки, воспринимаемые газом при наличии теплоотводящих проволочек и при их отсутствии.

где

Pp =a Еап^; Рэ

У ^Х ПР ^ГПР

^{2 а} К  _;

ак5э

„ _ F , n np Q np

где F = n d ВАЛ З ЩЕТ — общая плошадь контакта; d ВАЛ - диаметр вала; З щЕТ - ширина щетки; F' — площадь контакта за вычетом площади контакта проволочек; n _ПР – количество проволочек; Q _ПР –количество теплоты, отдаваемое в газ проволочкой.

Для определения количества теплоты, отдаваемого в газ проволочкой, воспользуемся известным в теплотехнике решением [8]

Q np = ^а п ^Fnp ^{( Т}К — ^ТГ ) ’ (2) где а _П = Х(3_ПРth ( Р_ПРl ) — условный коэффициент теплоотдачи, приведенный к корневому сечению (месту контакта проволочки с валом); X - коэффициент теплопроводности материала;

5 э = 25_к ; З к - толщина корпуса; h _Э - половина среднего расстояния между соседними проволочками.

И выражение для n _P принимает вид

* n p

=1-

n ПР FПР

-

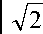
Z p

7

Р пр

2а ПР к 1

^{Х г}пр

^а ПР

коэффициент

теплоотдачи от проволоки к газу;

где а г - коэффициент теплоотдачи от вращающегося вала к омывающему его газу.

Однако для длинных, тонких и слаботеплоп-роводящих проволочек, а также при высоких значениях коэффициента а пр влияние наружной оболочки на усиление эффекта оребрения практически исчезает [8]. При величине pi >  3 погрешность составит не более 5%.

Таким образом, выражение для количества тепла, отводящегося от зоны контакта в газ через щетку

Q^pt = агFH P (TK - Tr ).   (3)

На рис. 2 изображена расчетная схема уплотнения. Его уравнение теплового баланса следующее

Q tP = Q щЕТ + Q i + Q 2 .       (4)

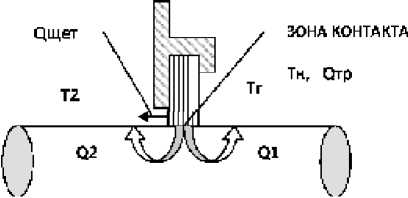
Рис. 2. Расчетная тепловая модель щеточного уплотнения

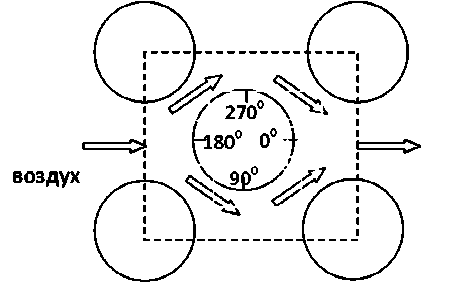
Рис. 3. Схема обтекания проволочки

Количество теплоты Q _ЩЕТ определяется выражением (3). Мощность трения вследствие малой утечки через контактную зону уплотнения практически равна тепловыделению Q _ТР в зоне контакта

^QТР = W ПОДЖ f ТР ^V .     (5)

где W _ПОДЖ – сила поджатия щетки к валу; f _ТР – коэффициент трения; V — скорость скольжения. Теплоотвод через вал можно определить аналогично теплоотводу от манжетного уплотнения [9].

Q i + Q 2 = Р вАЛ - вал \_ Р\ Тк - T ) + в ( Т — Т 2 )] , где Р ВАЛ — площадь сечения вала; - вал — коэффициент теплопроводности вала;

Nu = C Re n Pr m .

где Nu – число Нуссельта; Pr - число Прандтля; С,m,n – коэффициенты, зависящие от режима течения газа.

в1 =

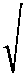
2ах

ВАЛ rВАЛ

; А =

^{2 а} 2

ВАЛ rВАЛ

;

Nu = 02 . Re = £VA,_pr__c^

2Г ;         ц ; Pr   2Г ,

где X — характерная длина; 2 г - коэффициент теплопроводности газа; V ₀ - скорость течения среды; d = 4 F_K П_K – характерный размер; F_K – площадь поперечного сечения канала; П_К – полный смоченный периметр; с _Р – теплоемкость газа.

В работе [6] были получены выражения для щетки

a i и а 2 — коэффициенты теплоотдачи от вала к газу и наружной среде.

Учет неоднородности прогрева вала может быть учтен через замену а на а^ д .

0.4 0.6

а г = 0,023 (pv 0 )О8 ciOpA-^ ц d

и для щеточного уплотнения

4а^R =а----ЭКВ 4 + Bi

Bi =

^{а Г}ВАЛ

² вал

а Г

0,4    0,6   0,8

0,8 Ор    2   8 РАД . З

= 0,023 (PV 0 ) Р 04  0,2 -------- ц d 8 РАД . Щ

Обычно Т_Г ~ T 2 и 0 1 = в ₂ . Если на вал нанесено теплоизолирующее покрытие толщиной 8 _ПОКР и с коэффициентом теплопроводности Х _ПОК р . то

Q i + Q 2 = F y t Тг_к - т г ) . (6)

где У т =

ПОКР +¹

Х покр  ^{2 2} ВАЛ ^FВАЛ Р 1

Подставляя (3), (5) и (6) в уравнение (4), получаем выражение для температуры в зоне контакта

TK

= ТГ +

Q ТР аГ F n* p + FyT

где 8 _РАд . З и 8 _РАд . щ - радиальные размеры выходного зазора и щетки.

Для определения коэффициента теплоотдачи от поверхности проволочек а пр можно воспользоваться выражениями для сеток /10/ или для материала МР, полученными в СГАУ Изже-уровым Е.А.:

Nu = 0,05 Re0,85 (сетка);Nu = 0,0452 Re1,28 (МР).

Приведенные выше формулы позволяют определить усредненное значение коэффициента теплоотдачи от поверхности проволочек а пр . На самом деле, из-за особенностей обтекания прово-

лочек охлаждающим газом его значение может

Для нахождения коэффициентов теплоотдачи пользуются известными интегральными соотношениями пограничных слоев [7]:

значительно отличаться на разных участках проволочки. Так, проведенное численное моделирование обтекания проволочки воздухом (рис. 3) с помощью пакета FLOTRAN позволило получить

распределение коэффициента конвективной теплоотдачи по периметру проволочки. При моделировании учитывались реальные расстояния между соседними проволочками. Пример распределения а пр приведен на рис. 4 (отсчет угловой координаты начинается с тыльной стороны проволочки). Проведенные исследования показали, что функция распределения а _Пр в окружном направлении существенно зависит от величины расхода воздуха, но практически не изменяется по радиусу щеточного уплотнения в пределах величины, равной радиальному размеру выходного зазора щеточного уплотнения.

Распределение температуры по длине проволоки

T = Tr + (Tk

Тг )

ch -l- [ 1 - Z 1 72

ГПР V l 7

ch J 2 Bik 1

_ ^ГПР

.

Подогрев воздуха, протекающего через уплотнение

^ T =

Проведенные расчеты показали, что за счет изменения плотности щетки можно изменять утечки и температуру в зоне контакта в широких пределах. Нагрев проволочек наиболее существенно происходит на расстоянии 0,2 l от корневого сечения, что согласуется с экспериментальными результатами /11/.При этом получено, что при более высокой пористости температура зоны контакта выше, так как ухудшается теплоотвод из зоны контакта (при одинаковой мощности трения, т.е. учитывается только теплосъем). Однако из-за более высокого расхода охлаждающего газа проволочки охлаждаются лучше, температура по их длине интенсивно падает, сравниваясь с температурой газа. Аналогичная картина наблюдается при малых значениях коэффициента теплопроводности материала щетки. Наибольшую трудность представляет определение мощности трения, особенно при вибрации вала. Здесь требуется проведение дополнительных исследований.

На рис. 5 приведено сравнение расчетных данных, полученных по предлагаемой теории, с экспериментальной зависимостью относительного подогрева волокон щеточного уплотнения в зоне контакта от приведенного расхода воздуха, полученной Гореловым Г.М. и др. [11]. Пара-

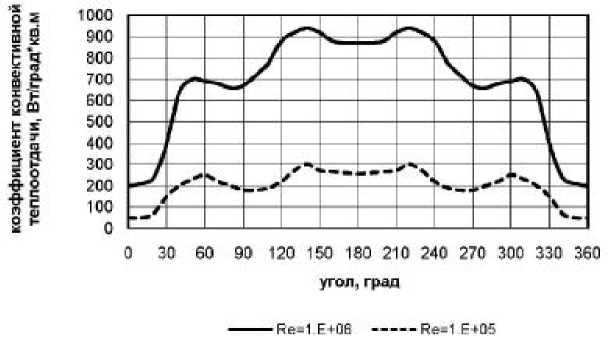
Рис. 4. Распределение коэффициента конвективной теплоотдачи от проволоки к газу в окружном направлении

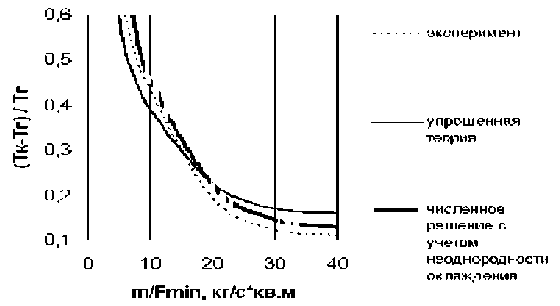
Рис. 5. Сравнение аналитических, численных и экспериментальных данных

метры исследованного щеточного уплотнения следующие: нихромовая проволока d =0,1 мм; плотность – 90 шт/кв.мм ; входной зазор – 5 мм; выходной зазор – 1 мм; толщина щетки – 1,5 мм; окружная скорость – 200 м/с. Анализ результатов на рис. 5 показывает удовлетворительное согласование аналитических и экспериментальных данных в зоне малых относительных расходов воздуха. В остальном диапозоне предлагаемая теория дает завышенный результат (погрешность до 50%). Несовпадение результатов можно объяснить как погрешностью эксперимента, так и тем, что при расчете некоторые исходные параметры брались осредненными, так как при проведении эксперимента не фиксировались. Учет распределения коэффициента конвективной теплоотдачи по поверхности проволочек, полученного численным моделированием в пакете FLOTRAN, позволил существенно снизить погрешность (до 10% в зоне малых расходов и до 20% в зоне повышенных расходов). Однако трудоемкость вычислений вырастает на несколько порядков.

Изложенная выше теория является аналитической, что существенно повышает ее значимость, так как можно провести оптимизацию параметров уплотнения. Поверочные расчеты рекомендуется проводить с использованием численного решения. Также на этапе проектирования появилась возможность определить температуру в зоне контакта и оценить надежность уплотнения.