Математическая модель синхронного генератора с системой самовозбуждения в режиме форсировки при несимметричных коротких замыканиях в энергосистеме
Автор: Горшков Константин Евгеньевич, Гольдштейн Михаил Ефимович
Журнал: Вестник Южно-Уральского государственного университета. Серия: Энергетика @vestnik-susu-power
Рубрика: Электроэнергетика
Статья в выпуске: 34 (167), 2009 года.
Бесплатный доступ
Разработана математическая модель синхронного генератора с системой самовозбуждения для анализа электромагнитных процессов в режиме форсировки при внешних несимметричных коротких замыканиях. В модели учитываются группы соединения обмоток трансформатора системы самовозбуждения, способы синхронного фазового управления тиристорным преобразователем и элементы автоматического регулятора возбуждения. Приведены результаты исследований режима форсировки блока ТГВ-200-2М.
Математическая модель, короткое замыкание, синхронный генератор, система самовозбуждения, тиристорный преобразователь, система управления тиристорами
Короткий адрес: https://sciup.org/147158080
IDR: 147158080 | УДК: 621.311
Текст научной статьи Математическая модель синхронного генератора с системой самовозбуждения в режиме форсировки при несимметричных коротких замыканиях в энергосистеме
В режиме форсировки синхронного генератора (СГ) при коротких замыканиях (КЗ) в энергосистеме питающие напряжения тиристорного преобразователя (ТП) системы самовозбуждения (ССВ) несимметричны по амплитуде и фазе [1]. Это приводит к неравномерному токораспределе-нию между тиристорами и, как следствие, к росту тепловых потерь и температуры тиристоров в наиболее нагруженном плече преобразователя. В работе [2] приведены способы управления преобразователем ССВ, позволяющие выравнивать длительности работы тиристоров. Для разработки алгоритмов управления и оценки их эффективности необходима математическая модель синхронного генератора, позволяющая исследовать зависимости тепловых потерь и температуры тиристоров от вида, удаленности, длительности КЗ и предшествующего режима работы синхронной машины.
В настоящее время широкое применение нашли математические модели синхронных машин, основанные на численном решении систем дифференциальных уравнений. Инвариантная запись системы уравнений Парка-Горева с уравнениями движения ротора и тиристорного преобразователя системы самовозбуждения позволяет получить модель любой степени точности и сложности. Для решения таких систем уравнений привлекаются специальные программные средства (MATLAB/ Simulink, Maple и др.), что исключает применение моделей в программах, использующих системы линейных алгебраических уравнениях.
В статье рассматривается математическая модель синхронного генератора с ССВ при несимметричных КЗ в энергосистеме с различными способами управления тиристорным преобразователем. В основе модели лежит приближенное реше- ние системы дифференциальных уравнений, выполненное в аналитической форме И.А. Глебовым [3, 4]. Такой подход позволяет использовать модель в программах расчета токов КЗ и дает возможности:
-
• рассчитывать режимы с произвольной длительностью КЗ без привлечения типовых кривых;
-
• исследовать работу элементов системы самовозбуждения в режиме форсировки;
-
• моделировать действия секции управления и регулирования ССВ (СУР).
На рис. 1 изображена эквивалентная схема замещения прямой последовательности СГ для начального момента времени при разных видах КЗ (п). Синхронный генератор представлен сверхпереходным сопротивлением х^, сопротивлением обратной последовательности х2, активным сопротивлением статорных обмоток га и ЭДС Ёф. Эквивалентное сопротивление прямой последовательности от выводов синхронного генератора до точки КЗ хвн^ в соответствии с методом симметричных составляющих можно записать как сумму сопротивлений повышающего трансформатора хт, эквивалентного сопротивления за трансформатором хЭКВф и добавочного сопротивления в точке КЗ Ах(п) [5]. Активное сопротивление внешней цепи учитывается сопротивлением обмоток повышающего трансформатора гт. Трансформатор системы самовозбуждения (ТСВ) представлен активным гтсв и индуктивным хтсв сопротивлениями, а также комплексным коэффициентом
±jN— трансформации Ктсв = Ктсве 6 , позволяющим учитывать группу соединения обмоток (N).
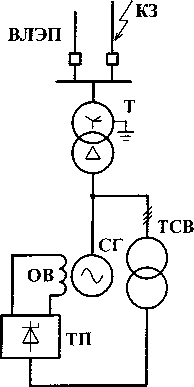
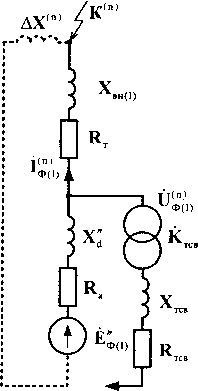
Рис. 1. Эквивалентная схема замещения прямой последовательности синхронного генератора с ССВ при несимметричном КЗ за повышающим трансформатором
Уравнения питающих напряжений ТП ССВ. Запишем обобщенное выражение для величин и углов линейных напряжений на вводах ТП при внешнем двухфазном КЗ между фазами «А» и «В» и однофазном КЗ фазы «С» в соответствии с работой [2]:
ил(0 =
7зе^(1)(о
----—--X
Ктсв
X —--------------—-----------
Фл =Рл +arctg
fx^+k^X, + x(n)_k(n)x С^“Л) ’
\ хвн к х2 7
где х^
k(n) =
^вн(1)+Ах(п);
О при К(3\
-
-1 при К*-2\
х(») — X
-
- ^ ВН(1) при К(1,1),
Х2+Хв„(1)
-
+1 при К(1);
(±N + 5)^wix Uдв, О
Г0 при 0 < ал < л, Рл = ] ~
-
[л при л < ал< 2л.
Углы ал и рл - величины, учитывающие группу соединения обмоток ТСВ. В выражениях запись «+N » соответствует схемам обмоток Yh/Y, Д/Д и Yh/Д, а запись «-N» соответствует Д/Yh. Для расчета величин при других видах КЗ достаточно изменить индексы напряжений в записи ал в соответствии с комбинацией замкнутых фаз.
Внешняя характеристика ТП ССВ. Современные тенденции увеличения единичной мощности тиристоров и уменьшения их числа в плече преобразователя, а также применение микропроцессорных СУР привели к отказу от разработки двухгрупповых систем возбуждения при проектировании СГ и замене существующих ССВ на одногрупповые при модернизации [6]. Для преобразователей таких ССВ не характерны режимы работы с большими углами коммутации тиристоров, в связи с этим достаточно получить внешнюю характеристику ТП для режима 2-3.
Управление ТП осуществляется многоканальной или одноканальной системой синхронного фазового управления тиристорами (МСУТ,
ОСУТ) с синхронизацией по линейным напряжениям питающей сети [7]. Запишем внешнюю характеристику тиристорного преобразователя при произвольном способе синхронизации СУТ. Обозначим углы смещения управляющих импульсов СУТ относительно моментов естественной коммутации тиристоров при угле управления ау = 0 как
8j 4 , 82 5 , е3 6. Формулы для расчета значений величин приведены в работе [2]. Используя выражение (1), внешнюю характеристику можно при
вести к виду
_ зУб ЕФ(1)(0 УА2(п,е) + В2(п,£)
71 К-тсв З^Хд+Х^)
( z ч А(п,е) xcos a (t) + arctg------
( J B(n,s)
тт _ ^ВнО
I = —
0 и
U0
2 л
2л У1-з+Y3-5+75-1
б
Гу 1(
d’
где A(n, s) = sin(8j) x i=l
^(^ +k(n)x2)2 -4x^k^x2 sin2(ai), з
B(n,8) = ^COS(8j)x i=l
ry, Ху - активное и индуктивное сопротивления коммутации преобразователя,
Yi-j - угол коммутации при выключении i-ro и включении j-ro тиристоров.
Несимметрия питающих напряжений ТП может приводить к появлению режима, который не наблюдается при симметричной работе. Значительное сближение последовательных интервалов коммутации двух тиристоров в анодной и катодной группах вызывает появление угла естественного запаздывания переключения. В результате две пары тиристоров переходят в режим 3-3. Угол естественного запаздывания может, как увеличивать, так и снижать несимметрию токораспределе-ния между тиристорами. Обозначим угол запаздывания i-ro тиристора как ф*. Тогда действительный угол включения тиристора а, = ау + 8, + Ф1_2-Для уточнения внешней характеристики ТП в выражении (2) следует заменить 8, на af - ау .
Уравнения синхронного генератора с ССВ. Для учета предшествующего режима работы СГ зададимся в относительных единицах значениями полной мощности So, коэффициента мощности cos (р0 и действующей величины напряжения на вводах ВН повышающего трансформатора Ubh0 . Тогда напряжение на выводах генератора и ток в статоре:
и V ивнО I
г2 + х2
Составляющие тока ротора в d, q-осях в предшествующем режиме:
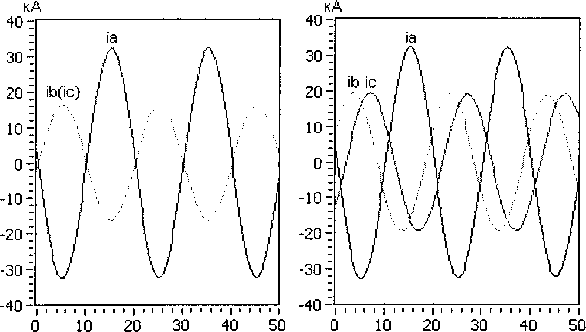
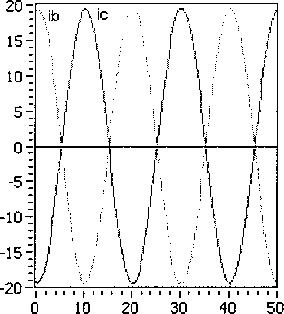
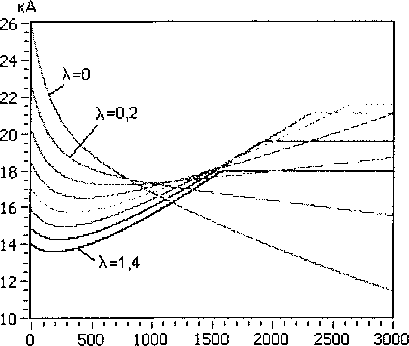
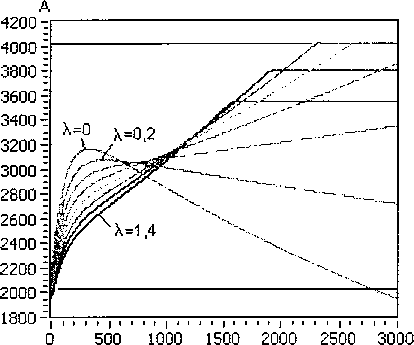
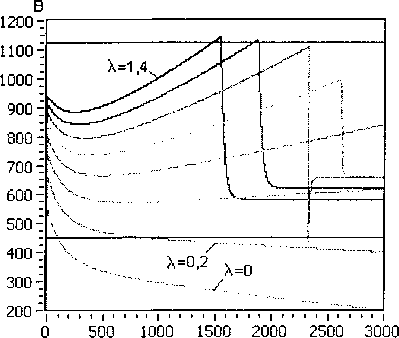
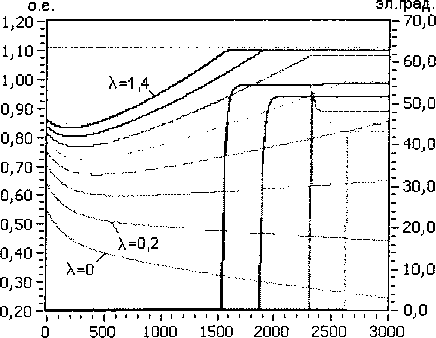
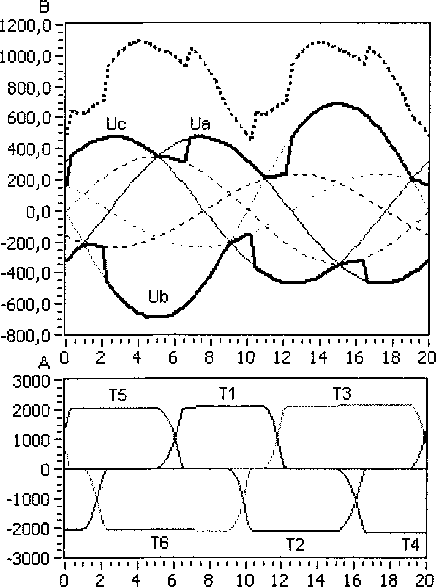
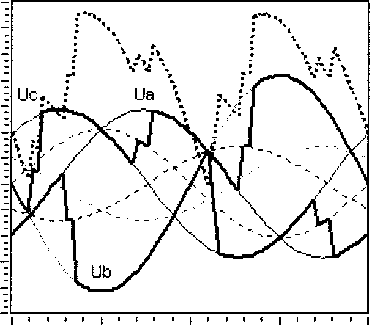
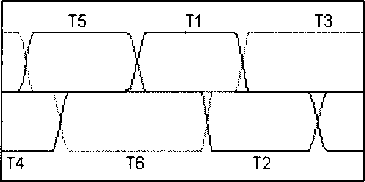
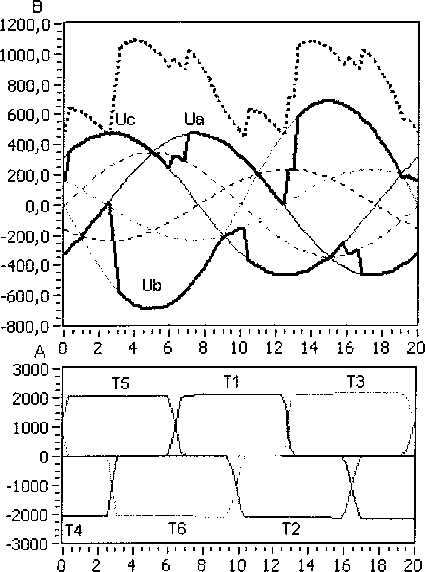
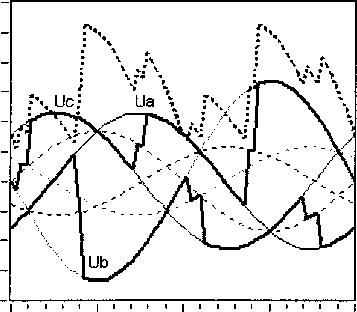
ido =1о8т(5о-ФоХ iqo =I0cos(80- где 80 = -arctg Ioxq COS Введем систему базисных величин напряжений (в вольтах) и токов (в амперах) для связи обмоток статора и ротора генератора: i6 - V2IH0M, If6 If xxxad> _ 7TT L _ 3u6i6 u6 ^3UHOM- ® 21й ■ Величина ЭДС синхронного генератора и тока возбуждения в долях от базисных значений: Eq0 =U0 cos80-id0xd, т _ Еч° 40 - xad Запишем систему дифференциальных уравнений синхронной машины в относительных единицах в операторной форме с учетом уравнения ТП ССВ и эквивалентного демпферного контура в продольной оси: Xd+X^ re+xadp XadP xad rf +rd+xfp xadP где re=---—- 71 Um xad xadP id x id rkd+XkdP Ikd (n,s) + B2(n,s) --------------X xcos ay(t) + arctg 3KTCB A(n,e)) B(n,s) J rd - xy + z э-------- r , ТЕ l бтГ ) Г Значения остальных сопротивлений можно найти, применив обычные схемы замещения синхронного генератора в продольной и поперечной осях. Приближенное решение системы уравнений относительно токов id и Id сводится к виду: ^(0 = 4^^^ (7) If(t) = I^oeP'«t +i?oeP2^t ^fOxad Но (Xd "Г Хвн ) гДе id0 =--;----7^-------+ id0 ; xd Хвн ’do ^Wad +’do(xd +Хвн)) (1) ~ (1) р Ad т Лвн Ad т Лвн у где iq0 = X2Jx ч-х^х lq0’ Aaq (Aq^ABH ^Akq rkq (Xq + Xbh -(хЧ+х™)ХкЧ Коэффициенты затухания составляющих токов получены путем разложения корней характеристического уравнения выражения (6) по степеням малых параметров и удержания только членов первого порядка малости. При более точном расчете можно учитывать члены второго порядка для этого достаточно умножить pj на (1-А) и р2 на (1 + А), если величины 1±А существенно отличаются от единицы. ^f0 ^f0 + ^fOxad + Ы0 (xd + хвн / fq^ xad I xd "Г хвн 1 (xkd xad)xadxd xd xd + xbhxfxkd — xad xad ^xd "^ xbh ) _-(rf+rd)(xd+XBH)) + rexad А I Pf А = I—+ l xfslJP2 xfsl xfsl (xkd-xad)xad (ха ~*"хвн )xkd "*"(xkd — xad)xad Xad Ре Xd+XBH)JP2’ гпех' -x 3Vi-3+b-5+Y5-iY. где xfsl — xf + 2 з xy v бтг у _(Xd-Xa)^ad xfx ,f2 3У’~3+УЗ-5+Т5-1Ъ ( l 6я p P2=-rkd xkd“xad+ --+ I xad 1______ hx^ Y1-3+Y3-5+Y5-1 6ll Система уравнений (6) описывает процессы в статоре и роторе довольно приближенно, отсутствует уравнение движения ротора, а также не учитывается влияние поперечной оси. В первом случае при малых длительностях КЗ (0,1-0,25 с) скорость ротора можно рассматривать постоянной, при больших длительностях необходим анализ взаимного влияния электрических машин, как это делается при расчете электромеханических переходных процессов. Во втором случае влияние токов в поперечной оси можно учесть, если составить более полную систему уравнений и решить ее относительно q-оси, после чего добавить решение к формулам (7): , z x xd + pf=(rf+ro)77>)x Ad abh xfx +(2-3^2I3zVH^lL T' l l 671 )) , Xd + Pe =re—--ГГХ x' +x Используя формулу для обобщенного вектора тока прямой последовательности генератора im(i) (t) = -^id (t) + i| (t) , находим мгновенные значения периодических фазных токов в статоре: iq(t) = i"0ep3rot iA(0 = - fcos(cot —)+k<n) cos(cot + ^)^im(1)(t), Ь(0 = -| . 5лх , z 5лх V z x cos( *с(0 = -| cos(ot+7) + k(n) cos(®t - 7) | im(i) (t). V 6 6 у Расчет углов коммутации тиристоров в выражении (7) следует выполнять рекуррентно, разбивая ось времени на интервалы малой длины. Такой прием используется повсеместно в про граммах расчета токов короткого замыкания произвольной длительности КЗ: Yi_j(t) = arccos cos осj- 2If(t)^r2+x2 и$ ^ил(1) иб при Для перерасчета питающих напряжений ТП ил (t) можно использовать выражение (1), если в него подставить равенство Наконец, зная величины основных составляющих токов обмоток генератора, несложно рассчитать среднее значение напряжения на обмотке возбуждения: Uf<0 = reim(1)(t)-frd +f2-MH^l54 L V(t). Рассмотренных выше уравнений достаточно для исследований и других параметров синхронного генератора и системы возбуждения. Используя выражение (1), можно найти напряжения на выводах СГ, а также построить диаграммы мгновенных значений напряжений на элементах ТП и его выпрямленного напряжения. Диаграмму токов тиристоров можно получить, если, используя выражения (8), записать уравнения коммутаций. Для перехода от относительных единиц к именованным значениям следует умножать токи и напряжения на одноименные базисные величины. Введение в модель элементов СУР. Основным элементом управления режимом синхронного генератора является автоматический регулятор возбуждения (АРВ). Рассмотрим простейший вариант АРВ с ПИ-регулятором и каналом регулирования по напряжению на выводах генератора [8]. Напряжение на входе регулятора ugW = to +k(n)x2)2 -4x^k(n)x2 sin2 Д + О +^(хвн) +k(n)x2)2 -Дх^к^Х;, sin2 (у) + +J(x^ + к(п)х2)2 -Дх^к^^з sin2(—) N 6)3 Сигнал управления, передаваемый в СУТ: ау ’ п = arccos AUycTkyi + ку2 £ AUyCTikyi Atj где AUyCT UyCT Ug, kyi, ky2 - коэффициенты усиления. Величину уставки представим таким образом, чтобы при снижении напряжения на выводах СГ ниже 85% появлялся режим форсировки: Uo, если Ug > 0,85, 2,5, если Ug <0,85. иуст = В установившемся режиме форсировки предельная допустимая величина тока возбуждения ограничивается двойным номинальным значением. Для этого предусмотрен блок ограничения тока ротора БОР-21. Сигнал управления, формируемый блоком: а у = arccos п А1усткуз + кУ2^ AIyCTjkyjAtj . i=l где А1уст =2,0-If ; куз - коэффициент усиления по току ротора. Условием вступления в работу БОР-21 является превышение током возбуждения двойного номинального значения If > 2If ном . При соотно шении сигналов AUyCT < А1уст управление возвращается к регулятору напряжения. Величины коэффициентов усиления пропорциональных звеньев в большинстве случаев можно принять равными 50 о.е. Для дифференциального звена величина коэффициента определяется индивидуальной настройкой. Исследование режима форсировки блока 200 МВт. В соответствии с изложенной методикой был выполнен расчет переходного процесса для блока турбогенератор ТГВ-200-2М с повышающим трансформатором ТДЦ-250000/110/15,75. Номинальные данные и параметры генератора: Рном =220 МВт, UH0M =15,75 кВ, 1НОМ=9490 А, cos (рном =0,85, Ufe0M -450 В, 1^^-2015 А, 1&х=70б A, xd =2,090, xd =0,357, х^ =0,233, xd-xad=0,213, х2=0,285, Td0=6,480c, Td =1,096 с, Td =0,137 с, Ta =0,326 с. Параметры обмоток блочного трансформатора: ukB_H=ll,3 % и Рк=651 кВт. Генератор оснащен тиристорной системой самовозбуждения с трансформатором Ун/Д-11 с параметрами: SH =3,6 MB A, U =902 В, uk =7,24 % и Pk =33 кВт. Исследования проводились для режима несимметричного КЗ на отходящей линии электропередач. Удаленность точки КЗ от вводов повышающего трансформатора задавалась как отношение X = хЭКВ0)/хт . Для линии электропередач Рис. 2. Периодические токи в статоре синхронного генератора в начале форсировки при двухфазном, двухфазном на землю и однофазном КЗ (А=1,0) Рис. 3. Действующее значение обобщенного вектора тока прямой последовательности im Рис. 4. Среднее значение выпрямленного тока обмотки возбуждения lf(t) Рис. 5. Среднее значение выпрямленного напряжения на обмотке возбуждения Щ1) Рис. 6. Напряжение на входе регулятора возбуждения Ug(t) и угол управления ory(t) на выходе В 1400,0 1200,0 1000,0 800,0 600,0 400,0 200,0 0,0 -200,0 -400,0 -600,0 -800,0 -1000,0 д3500 3505 3510 3515 3520 6000 т 4000 т 2000 т От -2000 т -4000 т -6000 а) 3500 3505 3510 3515 3520 б) Рис. 7. Диаграммы напряжений и токов элементов тиристорного преобразователя при двухфазном на землю КЗ (Х=0,6) в начале (а) и в установившемся режиме форсировки (б) В 1500,0 1250,0 1000,0 750,0 500,0 250,0 0,0 -250,0 -500,0 -750,0 -1000,0 д 5000 5005 5010 5015 5020 6000 4000 2000 0 -2000 -4000 -6000 а) 5000 5005 5010 5015 5020 б) Рис. 8. Диаграммы напряжений и токов элементов тиристорного преобразователя при двухфазном на землю КЗ (Х=0,6) при использовании ОСУТ с синхронизацией по напряжению Uc (UBc) отношение индуктивных сопротивлений нулевой и прямой последовательности принималось равным трем. В предшествующем режиме синхронный генератор работал с параметрами: S0=l, U0=l,l, cos (p0 = 0,85. В соответствии с выражениями (4) и (5) легко найти 10 =0,9 и If0 =0,93. На рис. 2 приведены кривые периодических фазных токов статора генератора при разных видах КЗ в одной и той же точке. Отдельный интерес представляет влияние на режим форсировки удаленности точки КЗ. Для этого были выполнены расчеты с Х=[0, 0,2, ..., 1,4], полученные кривые изображены на рис. 3-6. Исследуя характер изменения кривых, можно выявить границу зоны лавинообразного снижения напряжения на выводах генератора. В данном случае 0,2<\<0,4 для двухфазного на землю КЗ. На рис. 7 и 8 показаны диаграммы токов и напряжений элементов ТП ССВ. В первом случае для МСУТ с синхронизацией по линейным напряжениям питающей сети, во втором случае для ОСУТ с синхронизацией по напряжению Uc (UBc)- Из графиков видно, что способ управления тиристорами оказывает влияние на величину выпрямленного напряжения, а также на равномерность распределения длительностей работы тиристоров. Выводы. Таким образом, рассмотренная математическая модель синхронного генератора с системой самовозбуждения может быть полезна: 1. В программах расчета токов короткого замыкания для точного расчета при малых длительностях КЗ и приближенного при больших. 2. Для исследования влияния вида, удаленности и длительности КЗ на работу элементов системы самовозбуждения без привлечения специальных программ математического моделирования. 3. При изучении вопросов эффективного управления режимами работы синхронного гене-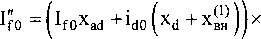
Список литературы Математическая модель синхронного генератора с системой самовозбуждения в режиме форсировки при несимметричных коротких замыканиях в энергосистеме
- Гольдштейн, М.Е. Исследование работы системы самовозбуждения синхронного генератора при внешних несимметричных коротких замыканиях/М.Е. Гольдштейн, К.Е. Горшков//Вестник ЮУрГУ. Серия «Энергетика». -2008. -Вып. 10. -№ 26(126). -С. 36-41.
- Гольдштейн, М.Е. Токораспределение между тиристорами в преобразователе системы самовозбуждения синхронного генератора при внешних несимметричных коротких замыканиях в энергосистеме/М.Е. Гольдштейн, К.Е. Горшков//Вестник ЮУрГУ. Серия «Энергетика». -2009. -Вып.11.-№15.-С 10-16.
- Глебов, И.А. Системы возбуждения синхронных генераторов с управляемыми преобразователями/И. А. Глебов. -М.; Л.: Изд-во АН СССР, 1960. -335 с.
- Глебов, И.А. Электромагнитные процессы систем возбуждения синхронных машин/И.А. Глебов. -Л.: Наука, 1987. -344 с.
- Руководящие указания по расчету токов короткого замыкания и выбору электрооборудования/под ред. Б.Н Неклепаева. -М.; Изд-во НЦ ЭНАС, 2002. -152 с.
- Логинов, А.Г. Системы возбуждения турбо-и гидрогенераторов ОАО «Электросила»/А.Г. Логинов//Электротехника. -2003. -№ 5.-С 43-48.
- Писарев, А.Л. Управление тиристорными преобразователями (системы импульсно-фазового управления)/А.Л. Писарев, Л.П. Деткин. -М.; Энергия, 1975. -264 с.
- СО 34.45.629-2002. Методические указания по техническому обслуживанию микропроцессорных АРВ и систем управления силовых преобразователей систем возбуждения генераторов. -М.: СПО ОРГРЭС, 2003.


