Математическая модель системы символьной синхронизации наземной приемно-регистрирующей станции телеметрической информации в условиях флуктуаций амплитуды сигнала

Введение1234

В настоящее время происходит значительная модернизация изделий ракетно-космической техники. Так, в последние годы разработаны пер спективные рак етоносители семейств «Союз» и

«Ангара», а также осуществлено обновление и восполнение орбитальной группировки космических аппаратов. Исходя из данного направления развития космической отрасли государства, количество летных испытаний изделий ракетнокосмической техники будет значительно возрастать. Вследствие этого к наземным радио-телеметрическим станциям предъявляются всё более жесткие требования в отношении достоверности и полноты регистрации телеметрической информации о состоянии работы бортовой аппаратуры [1]. Одним из основных направлений повышения полноты и достоверности за- регистрированной телеметрической информации является разработка перспективных систем приема телеметрической информации, учитывающих различные особенности передачи группового телеметрического сигнала по радиоканалу Анализ процессов передачи телеметрической информации по радиоканалу показал, что значительное влияние на качество приема телеметрической информации оказывают случайные флуктуации амплитуды группового телеметрического радиосигнала. При этом, исходя из структуры приемно-регистрирующей станции телеметрической информации, определено, что наиболее значительное влияние случайные флуктуации амплитуды принимаемого сигнала оказывают именно на систему символьной синхронизации. Следовательно, разработка новых подходов построения системы символьной синхронизации наземной приемно-регистрирующей станции, учитывающих случайные флуктуации амплитуды принимаемого сигнала, позволит повысить полноту и достоверность регистрируемой телеметрической информации [2].

Постановка задачи по разработке математической модели системы символьной синхронизации наземной приемно-регистрирующей станции телеметрической информации

В целях формализации задачи по разработке математической модели системы символьной синхронизации радиотелеметрической системы, функционирующей в сложных условиях приема сигнала, следует установить математические зависимости между источником сообщения, переносчиками сообщений и каналом связи, влияющим на передаваемый сигнал [3]. Способом, содействующим установлению данных зависимостей, является формализованное описание процесса передачи телеметрической информации от бортовой аппаратуры потребителю, представленное на рис. 1.

ВЕСТНИК 2017

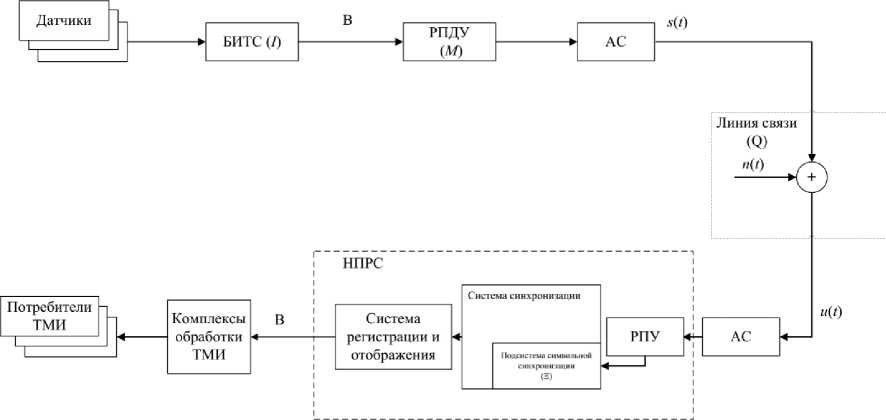
Рис. 1. Структурное описание процесса передачи телеметрической информации

На рис. 1 сокращения соответствуют: БИТС -бортовая информационно-телеметрическая система, РПДУ - радиопередающее устройство, АС - антенная система, РПУ - радиоприемное устройство, ТМИ - телеметрическая информация.

При данном рассмотрении системы передачи информации в качестве сообщения b следует рассматривать одиночный бит слова, принимающий значения информационного параметра X, равного 0 или 1. Вследствие этого на выходе бортовой информационно-телеметрической си- стемы после опроса всех датчиков за время сеанса измерения Tси передаваемая информация представляется в виде по следовательности бит В = {b р b2, _bk}, при этом b сопоставляется со значением информационного параметра X, i = 1,k; X е Л = {1,2}, где Л - пространство значений передаваемых бит. Исходя из задач применения системы символьной синхронизации, заключающихся в точном определении временных границ следования бит и опознавании их информационных значе- ний, время проведения сеанса измерений представляется множеством интервалов времени приема одиночных бит и описывается в следующем виде Tux = tt0, t1] С Tc.„., t0 G TCJ|., t! e Tc.u., t! > t0 -время приема первого бита, Tut = [tk- 1, tk ] с Тси , tk--1 G Тс.и., tk G TLu.» tk > tk-1 - время приема k-го бита.

В радиопередающем устройстве сообщение b ₁, выражающееся в значении информационного параметра λ, преобразуется в сигнал s . Математически данная операция отображения передатчиком информационного параметра λ в сигнал s описывается следующим образом:

s → M (λ), (1) где M представляет собой оператор, с использованием которого задается способ формирования сигнала передатчиком, то есть определяется выбор переносчика информации и способа кодирования. При этом, в радиотелеметрических системах, вследствие большого объема передаваемой информации, помехоустойчивое кодирование не применяется. Следовательно, в качестве оператора M следует рассматривать вид модуляции передаваемого сигнала, в данном случае рассматриваются модуляции FSK и PSK.

В линии связи на передаваемый сигнал s воздействует возмущающая среда Q. В соответствии с этим, групповой телеметрический сигнал, поступающий из линии связи на вход системы символьной синхронизации, описывается следующим выражением:

u = Q( s , n ), (2) где u – искаженный сигнал на входе наземной приемно-регистрирующей станции;

n – белый гауссовский шум.

Действие возмущающей среды Q проявляется не только в форме аддитивного воздействия на передаваемый сигнал, но и в виде появления случайных изменений (флуктуаций) вектора информационных параметров сигнала α .

Постановка задачи по разработке математической модели системы символьной синхронизации радиотелеметрической системы, функционирующей в сложных условиях приема сигнала, сводится к следующим положениям.

Дано:

• 1)    параметры канала передачи группового телеметрического сигнала от бортовой аппаратуры потребителю, представляемые следующим теоретико-множественным описанием

D = { M , H , Q, I ; u ( t )}, (3) где M – вид модуляции передаваемого сигнала;

H – структура кадра группового телеметрического сигнала, определяющая потенциальные возможности по восстановлению тактовой частоты, на основе синхровставок, скремблеров и синхронизирующихся кодов;

Q – множество параметров возмущающей среды, которые характеризуют сложные условия приема группового телеметрического сигнала, приводящие к флуктуациям параметров α группового телеметрического сигнала и снижению отношения сигнал/шум на входе приемного устройства;

I – информативность бортовой радиотелеме-трической системы, которая определяет интервалы времени передачи сообщений b за время проведения сеанса измерений T _с.и., τ _и = ¹ _I ;

u ( t ) – принимаемый групповой телеметрический радиосигнал:

u ( t ) = n ( t ) + s i ( t; a ), i = 1,2,          (4)

где α = α ₁, α ₂,... α _m – вектор информационных параметров передаваемого сигнала, подверженных флуктуациям;

• 2)    накладываемые ограничения Δ:

• – V – требования к скорости передачи информации, определяющие отсутствие возможностей использования синхровставок и синхропоследовательностей;

  – g – априорные законы распределения вероятностей флуктуирующих параметров принимаемого сигнала.

Требуется формализовать математическую модель системы символьной синхронизации наземной приемно-регистрирующей станции Ξ, с учетом параметров канала передачи группового телеметрического сигнала D и накладываемых ограничениях Δ.

Математическая модель системы символьной синхронизации наземной приемно-регистрирующей станции телеметрической информации на основе многоканального поиско-порогового обнаружения

При вхождении в символьную синхронизацию наземной приемно-регистрирующей станции на вход приемного устройства поступает сигнал следующего вида:

u ( t ) = n ( t ) + es i (t ; ф,т), i = 1,2,        (5)

где t – интервал наблюдения сигнала, t е ( т , т и + т );

n ( t ) – белый гауссовский шум;

ε – случайная интенсивность принимаемого сигнала (флуктуирующая амплитуда);

φ – случайная фаза принимаемого сигнала;

τ – неизвестная временная задержка принимаемого сигнала.

ВЕСТНИК 2017

Априорный закон распределения вероятностей случайной фазы принимаемого сигнала описывается следующим выражением:

z z    ^-,Ф е (0,2 П )

p (Ф) = 1 2п             .           (6)

0, ф е (0,2 п )

ВЕСТНИК 2017

Вследствие сложных условий передачи группового телеметрического сигнала при вибрации изделий ракетно-космической техники, вращении корпуса и разделении ступеней изделий возникают случайные временные флуктуации амплитуды сигнала. В теоретических выкладках к существующим моделям обнаружения почти всегда вводится модель рэлеевских флуктуаций, несмотря на то что известны частые и серьезные отклонения от этой модели [4]. В работе [5] подчеркивается, что, в соответствии с экспериментальными исследованиями при интервалах наблюдения не более нескольких минут, мгновенные значения сигнала в 20–40 процентах случаев распределены по закону Рэлея. В остальных случаях наблюдается обобщенный закон Рэлея.

Следовательно, в качестве априорного закона распределения вероятностей флуктуаций амплитуды сигнала при разработке модели системы символьной синхронизации следует рассматривать обобщенный закон Рэлея, описываемый следующим выражением:

Р (е) = «

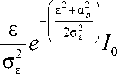
^еа p 1

-2 у при 0 < _Е <- , (7)

0,                  при е <  0

где ε – коэффициент, характеризующий нормированные амплитудные флуктуации сигнала;

α _p ² – мощность регулярной составляющей коэффициента ε;

2σ_ε ² – мощность флуктуационной составляющей коэффициента ε;

I ₀ – модифицированная функция Бесселя первого рода нулевого порядка.

В целях разработки модели символьной синхронизации использован широко известный и распространенный подход, основанный на многоканальном поиско-пороговом обнаружении [6]. Для реализации данного подхода на первом этапе разработки определена функция правдоподобия принимаемого сигнала p ( uS ) . Для вывода функции правдоподобия рассмотрен некогерентный прием сигнала с неизвестными начальной фазой и интенсивностью, который заключается в использовании квадратурного приемника.

В рассматриваемой задаче на основе разложения принимаемого радиосигнала на квадратурные составляющие выделяется низкочастотный видеосигнал, отображающий передаваемое сообщение. Квадратурные составляющие описываются следующими выражениями:

s = s ( t ) cos( ^ ₀ 1 + Ф( t ))

s = s (t )sin(^01 + Ф(t))’ где s(t) и Ф(t) – законы изменения амплитудной и угловой модуляций сигнала при передаче сообщений.

Опорный сигнал s, используемый для разложения на квадратурные составляющие, можно представить в виде комплексного аналитическо- го сигнала:

5 = 5 + js _±= s ( t ) e ^{( j} -t ^{+ Ф (} t ».

Функции правдоподобия p ( u/_s ) для сигнала со случайной интенсивностью и начальной фазой определяются в соответствии с выражением

2 п го

P ⁽ “Л ) = k- ! i P ( u/s .Е.ф.Т ) P ⁽ Ф ) P ⁽ = ) dФ^d =, ⁽¹⁰⁾ где k_u – коэффициент, отражающий гипотезу о наличии на входе приемного устройства белого гауссовского шума.

Подынтегральное выражение для формулы (10) описывается так:

p U = ke ^p (/ s ,е,ф ) u

1 г

-       ( u ( t ) - s ( t ;е,ф))² dt

N

,     0 0

T

- I E —[⁽ u ⁽ t ) ^{s (} t ;ф)) dt

= k u e N ⁰ e ⁰⁰

.

В соответствии с разложением принимаемого сигнала на квадратурные составляющие, интеграл, входящий в выражение (11), записывается в виде:

TT j u (t^s(t; ф) = cos ф j u(t)s(t)dt -0                             0

T

• - sin ф j u ( t ) s _± ( t ) dt .               (12)

Для дальнейшего вывода функции правдоподобия использованы следующие выражения:

T

Y = j u (t) s (t) dt = Z cosy;(13)

T

• У^=| u (t) s±( t) dt = Z sin v;(14)

Z = jY2 + Y±2;(15)

Ф = arctg —,(16)

где Z – модульное значение корреляционного интеграла, а ψ – фаза.

Исходя из определения аналитического сигнала (9), выражение (15) можно представить в следующем эквивалентном виде:

С учетом выражения (22) выражение (21)

перепишется в следующем виде:

T

Z = j u ( t ) .$( t ) dt .

С использованием данного выражения и с учетом случайной интенсивности принимаемого сигнала формула (13) преобразуется к виду:

T

J e u ( t ) s ( t , ф ) dt = e Z cos ( ф + у ) . (18) 0

→

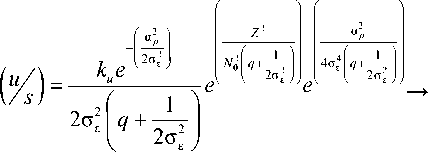
I 0

Z α _p

N o ^ 2 к

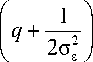
При использовании выражений (16) и (18) формула (11) приводится к следующему виду:

,           ² г , - — (~ ( Z ■'■ + *>

Р ( u/s ) = k“ If e ^{0 e 1N}”          P ⁽Ф) P ^{(e) d} Ф d ^e . (19)

0 0

При проведении интегрирования выражения (19) по переменной φ, с учетом априорного закона распределения вероятностей случайной фазы,

получено

p

- f ^E 2 E 1

(/ ) = k . г ^¹ N • ^J i■

2e Z |

— I p (e) d e. (20) . ^N • )

Таким образом, выражение (23) описывает функцию правдоподобия в условиях приема группового телеметрического радиосигнала со случайной начальной фазой и амплитудой, флуктуирующей по обобщенному закону Рэлея. Данные условия наиболее полно характеризуют этап выведения изделий ракетно-космической техники при проведении их испытаний на космодромах.

На втором этапе для формализации матема-

С учетом априорного закона распределения вероятностей флуктуаций амплитуды, описываемого обобщенным законом Рэлея, выражение (20) преобразуется:

тической модели системы символьной синхронизации определено отношение правдоподобия. При выводе отношения правдоподобия, характеризующего логику работы обнаружителя, рас-

сматриваются две гипотезы: первая гипотеза

характеризует принятие решения о приеме сиг-

" 4 " E } p ( u/s ) = J e ¹ N0 ^J I 0

нала при условии, что на вход системы синхро-

ВЕСТНИК 2017

^ 2"Z)

<     )

( sa„ ^

#1 dE =

I 2°e )

низации поступало информационное сообщение

p ( u/s ) ,

а вторая гипотеза – о приеме сигнала при

k u

=2.J

εe

( _E 2 q )

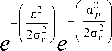
I 0

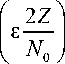
I 0

к

αp ε

2 σ ε ²

dε ^,

E где q - отношение сигнал/шум, q =   . При вы-

N ₀

полнении преобразования получено:

условии, что на входе системы синхронизации был шум p ( ц / ) .

Отношение правдоподобия определено в соответствии со следующим выражением:

^{p (} u/s ) -

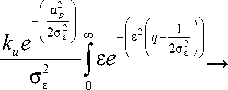
p ( us ) Л p ⁽ us _1Е,ф,т ) p <^ф> p <=> ^{d ф} d =

■ p (/)"            p ( un )            .' )

→ I ₀

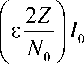
к

ε ^p d ε.

2^ 2 J

Основываясь на том, что условная плотность вероятности приема колебания u ( t ) при условии, что сигнал отсутствует, p ( u /) определяется выражением ⁿ

Внутренний интеграл выражения (21) является табличным:

p

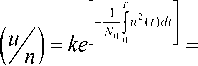
Г 2                                         1

j xe p 1 0 ( bx ) 1 ₀ ( cx ) dx = —e1 ₀

отношение правдоподобия при приеме сигнала с неизвестным временем задержки и флуктуирующей амплитудой оценивается формулой:

→

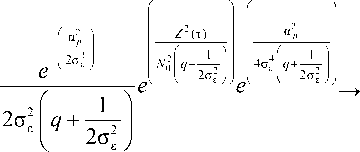
Z ^(т)а p

N 0 ^ 2

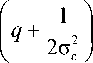
ВЕСТНИК 2017

Исходя из того, что для обеспечения равенства E = e ² E = a ²E + 2a 2 E , следуют следующие равенства a ² + 2a ² = 1 и Y 2 + 1 = 1 2 .

p ε                     ₂σ_ε

Используя широко известный параметр распределения Райса, характеризующий глубину за-2 α2p мираний и определяемый как γ =     2 , отно-

2σε шение правдоподобия перепишется в виде:

₀                  f Z ²(t) 1 f Y ²(Y² + 1) 1

e ^Y (Y ² + 1) I N 02 ( q + Y² + 1 ) I I ( q + Y² + 1 ) I

L = ₇—— ---₇e ^V '     '^Je ^vv     ^

( q + y + 1 )

Z (T) _A 1

^^^^^^B

^ I 0

n о ( q + y² + 1 )

.

V                             2

Из выражения (27) определено, что отношение правдоподобия при постоянной глубине замираний является монотонной функцией Z и поэтому может быть записано следующим выражением:

т (      Z ²(t)     )

L = exp I N^+T)}     ⁽²⁸⁾

В соответствии с выражением (28), логика работы поиско-порогового обнаружителя заключается в расчете отношения правдоподобия L и сравнения полученного значения с порогом L ₀.

Исходя из выражения (28), для принятия решения об обнаружении границы следования бит, на основе сравнения отношения правдоподобия с порогом, необходимо получить оценки глубины замираний принимаемого сигнала и отношения сигнал/шум в радиоканале передачи информации. Вследствие этого данное выражение целесообразно переписать в следующем виде:

(      ^Z ²(t)     )

^L = exp ay2z- -2 n .      (29)

( N o² ( q[ + Y'² + 1) J

Для получения оценки глубины замираний γˆ ² необходимо получить оценки мощности регулярной αˆ ² _p и флуктуационной составляющей амплитуды сигнала 2σ^ˆ_ε ² , что соответствует нормированной оценке амплитуды сигнала a 2 ; + 2a 2 = ё. Оценка модуля корреляционного интеграла Z²(t) позволяет, при достижении им максимального значения и превышении порога обнаружения, получить оценку времени задержки принимаемого сигнала τˆ , что в приложении к решаемой задаче является определением границы следования бит.

На практике, в режиме непосредственного приема информации, реализация схемы приемного устройства в соответствии с выражением (29) и получение прямыми измерениями оценки глубины замираний γˆ ² , а также оценки отношения сигнал/шум в радиоканале передачи данных, q ˆ является технически сложнореализуемым. Поэтому для получения данных оценок

используются косвенные методы, основанные на статистической оценке значений модуля корре-

ляционного интеграла, результаты применения которых учитываются при формировании порога обнаружения. Это обусловлено тем, что на зна-

чение модуля корреляционного интеграла непосредственно влияет амплитуда сигнала и шумы

радиоканала:

Л

Z =

T

j ( n ( t ) + e s ( t ; ф,т)) , v ₁( t ) dt

Вследствие этого, при отношениях сигнал/ шум более 10 дБ используют более простую

многоканальную квазиоптимальную решающую схему, основанную на оценке модуля корреляци-

онного интеграла в каналах с различным време-

нем задержки принимаемого сигнала, на основе

следующего выражения:

L = exp

²⁴ a Z m ²

n o² ( q + Y ² + 1)

= Z, m     Z mm >z0  _>  т,

max

где Z_m ² – значение модуля корреляционного интеграла в каналах обнаружителя;

Z ₀ – порог обнаружения.

Реализация одного канала схемы, основанного на выражении (31), представлена на рис. 2.

Таким образом, основываясь на выражениях, описывающих отношение правдоподобия при приеме сигнала с неизвестным временем задержки, случайной начальной фазой и флуктуирующей по обобщенному закону Рэлея амплитудой, реализуется математическая модель системы символьной синхронизации и определя-

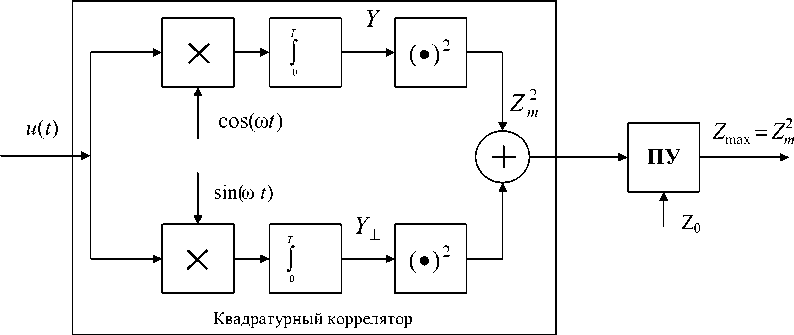
Рис. 2. Канал поиско-порогового обнаружителя границ следования бит

ется структура многоканального поиско-порогового обнаружителя границ следования бит.

Оценка адекватности математической модели системы символьной синхронизации на основе многоканального поиско-порогового обнаружения в условиях флуктуирующей амплитуды принимаемого сигнала

При синтезе устройств символьной синхронизации на основе многоканального поиско-порогового обнаружения необходим выбор критерия качества работы данного устройства. Поскольку теория статистических решений охватывает всё многообразие статистических критериев, целесообразно при решении задач синтеза устройств символьной синхронизации на основе многоканального поиско-порогового обнаружения воспользоваться результатами этой теории.

С учетом решения задачи обнаружения именно на этапе вхождения в символьную синхронизацию при обнаружении границ следования бит, целесообразно использовать критерий Неймана – Пирсона, который гарантирует, что вероятность ошибки типа «ложная тревога» не превысит заранее выбранной величины, а вероятность ошибки «пропуск сигнала» будет минимальной. Критерий Неймана – Пирсона не требует знания априорных вероятностей присутствия и отсутствия сигнала, а также функции потерь.

При использовании критерия Неймана – Пирсона для обнаружения границ следования бит возможны два типа ошибок. Первый тип ошибок заключается в том, что принимается решение об обнаружении границ следования бит, в то время как в принимаемом сигнале их нет, что может быть обусловлено либо отсутствием

сигнала на входе, либо следованием бит одинакового значения. Данный тип ошибок приводит к вхождению в ложную синхронизацию и численно определяется вероятностью ложного обнаружения F . Вероятность ложного обнаружения является условной вероятностью превышения

модульного значения комплексного корреля-

ционного интеграла порогового значения при условии отсутствия границы следования бит и

определяется выражением [9]:

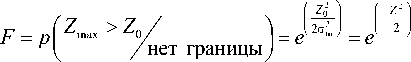
, (32)

где σ_ш ² – дисперсия огибающей на выходе квадратурного детектора при воздействии шума со

спектральной плотностью N ₀;

Z – порог обнаружения, Z = ₂ ⁰ .

σш

Второй тип ошибок заключается в том, что решение об обнаружении границы следования бит не принимается, в то время как в принимаемом сигнале присутствует переход между битами. Данный тип ошибок называется пропуском сигнала. Вероятность пропуска сигнала является условной вероятностью непревышения модульного значения комплексного корреляционного

интеграла порогового значения при условии наличия границы следования бит и определяется выражением [7]:

^e = p

max

/ есть граница у

Вероятность пропуска границы следования бит составляет полную группу событий с вероятностью правильного обнаружения границы D. При воздействии на вход системы символьной

синхронизации смеси принимаемого сигнала с флуктуирующей амплитудой, с условием фик-

ВЕСТНИК 2017

сирования её значения и фазой, а также гауссовских шумов вероятность правильного обнаружения определяется, как [10–11]:

^

D(e)=/ p (Ze) dZ=

Z 0

отношения сигнал/шум при различной глубине замираний и вероятности ложного обнаружения с учетом рассмотрения одного канала обнаружителя для разработанной модели системы символьной синхронизации.

где ^p

^

- /

e EZ

Z 0

σ ш²

σ ²

dZ

,

( Z /) - плотность вероятности огибающей

сигнала при ε = const, описываемой обобщенным распределением Рэлея;

E – энергия принимаемого сигнала без замираний.

Полная вероятность правильного обнаружения определяется путем усреднения выражения (34) по всем значениям e:         , 2 2 ^

^

^

D = j D (е) p (е) d е = j

z 0

Z

„2 2

σσ шε

→

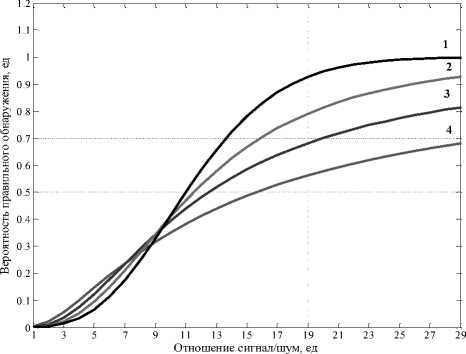
Рис. 3. Характеристики обнаружения при F = 10^-4 1) γ = ∞; 2) γ = 10; 3) γ = 3; 4) γ = 0

to I

^ J E ^

— i

EL + -4 JI

° ™ 2^ 1 ))г

⁾ I 0

e EZ

2 I I 0 ° ш )

10»

° J

d ε dZ . (35)

ВЕСТНИК 2017

С учетом (22) выражение (35) для вероятности правильного обнаружения сигналов с флуктуирующей по обобщенному закону Рэлея амплитудой запишется в более компактной форме [12]:

D = Q ( q, h ),

E p где q = 2- = σ

2a 2p E  '

2о 2 E + N о _?

1 2

h = Z_L = Г 2 Z0 /Е ) о ² ( 2^ 2 Е + N ₀,

α p (2 E N 0 )¹² ;

(1 + 2о 2 E/N о )¹² ;

Z

1 ^;

(1 + 2о 2 EJN _D/²

Q – функция Маркума.

Выражение (36) при приеме телеметрического радиосигнала с флуктуирующей амплитудой целесообразно записать через параметр обобщенного распределения Рэлея, который характеризует глубину замираний амплитуды принимаемого сигнала. Опираясь на то, что а2; + 2а| = 1 и Y2 +1 = % 2, аргументы функции Маркума 2σε в выражении (36) записываются в следующем виде [12]:                              1

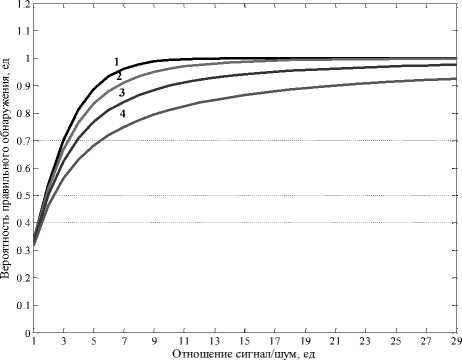
Рис. 4. Характеристики обнаружения при F = 10-1 1) γ = ∞; 2) γ = 10; 3) γ = 3; 4) γ = 0

q =

2 E

γ ²

-------*------------------:----------------—

N о 1 + y² + ( EJN о )

;

h = 2ln | Y I F

1 + y ²

1 + Y 2 + ( EJN о )

. (40)

На рис. 3 и 4 представлены результаты оценки вероятности правильного обнаружения от

Достоверность полученных результатов, а вместе с тем и адекватность разработанной математической модели системы символьной синхронизации на основе многоканального поископорогового обнаружения в условиях флуктуаций амплитуды принимаемого сигнала по обобщенному закону Рэлея, подтверждается тем, что в случае отсутствия флуктуаций ( 2 a ; ² = 0 ) данные результаты совпадают с вероятностью правильного обнаружения для случая некогерентного обнаружения со случайной начальной фазой, а в случае флуктуаций амплитуды по закону Рэлея

( a p = 0 ) полученные результаты совпадают с вероятностью правильного обнаружения для случая некогерентного обнаружения со случайной начальной фазой и рэлеевским распределением амплитуды.

Заключение

Таким образом, в статье представлена математическая модель системы символьной синхронизации наземной приемно-регистрирующей станции телеметрической информации, функционирующей в условиях случайной начальной фазы и флуктуирующей по обобщенному закону Рэлея амплитуды принимаемого сигнала. Разработанная модель построена на основе широко известных в статистической теории связи подходов, основанных на многоканальном поископороговом обнаружении. Адекватность разработанной модели подтверждена на основе оценки характеристик обнаружения системы символьной синхронизации, результаты которой в частных случаях отсутствия флуктуаций и при флуктуациях амплитуды по закону Рэлея совпадают с теоретическими результатами и результатами других авторов, занимавшихся исследованиями в данной предметной области. Разработанная модель символьной синхронизации может быть применена при создании перспективных наземных приемно-регистрирующих станций телеметрической информации.