Математическая модель системы управления pH в in vitro модели желудочно-кишечного тракта домашней птицы

Введение. Существенная нелинейность химических реакций кислот и оснований определяет алгоритмы управления в режиме подкисления или подщелачивания, то есть периодической дозации минимального объема кислоты или щелочи. Такое регулирование может быть малоэффективным, т. е. допускает недостаточную или избыточную концентрацию контролируемого вещества. Статья посвящена проблеме точного регулирования водородного показателя в мини-биореакторах. Предлагается использовать цифровую модель системы управления кислотностью для подбора концентраций доливаемых растворов, определения методики регулирования и повышения точности. Цель работы — обеспечение требуемой точности регулирования рН в in vitro мини-модели желудочно-кишечного тракта статического типа.

Материалы и методы. Исходная структурная схема модели включает накопители и потоки. Она представляет собой базу для основных дифференциальных уравнений, характеризующих изменение объема и кислотности. Для корректировки показаний кислотности результирующего раствора по температуре создана статическая модель, основанная на полиномиальной аппроксимации экспериментальных данных методом наименьших квадратов. В прикладном пакете Matlab Simulink исследованы структурные элементы математической модели. На реальной системе in vitro моделирования искусственного желудочно-кишечного тракта домашней птицы определены переходные характеристики для подтверждения адекватности математической модели.

Результаты исследования . В рамках данной работы авторы создали и проанализировали нелинейную математическую модель изменения pH в биореакторе с учетом внешних управляющих воздействий. Потоки раствора соляной кислоты, раствора щелочи и слива раствора из реактора представлены как элементы дифференциального уравнения, описывающего накопление жидкости в реакторе. Для повышения точности решение доработали с учетом температурной зависимости водородного показателя. Предложена математическая модель дозирования на основе регулятора с каналами щелочи и кислоты. Полученные данные позволили генерировать объединенную модель процесса регулирования pH в биореакторе. Адекватность решения подтвердили опытным путем. В виде структурных схем показаны модели: регулятора pH, регулирования объема содержимого в реакторе и химических реакций. Сравниваются переходные процессы математической модели и реальной системы управления. Установлено, что переходные характеристики математической модели и реальной системы идентичны по времени регулирования. Относительная погрешность регулирования реальной системы составила 0,35 %, а математической модели — 0,1 %, что соответствует требуемой точности регулирования ±0,1 pH. В виде графиков показано влияние исследованных потоков на реакцию нейтрализации.

Обсуждение и заключения . Предлагаемая математическая модель позволит подобрать оптимальные методы и алгоритмы регулирования кислотности, что ускорит создание регулятора нелинейного процесса регулирования водородного показателя. В будущем эти наработки можно интегрировать в комплексную цифровую модель всего искусственного желудочно-кишечного тракта домашней птицы для оптимизации алгоритмов управления (дозации, перемешивания, периодичности и т. п.), а также аппроксимации к объектам in vivo.

Информатика, вычислительная техника и управление

Original article

Mathematical Model of the pH Control System in an In Vitro Model of theGastrointestinal Tract of Poultry

Danila Yu Donskoy¹    , Alexandr D Lukyanov¹    , Vladimir Filipović ²   , Tamara B Asten¹

• ¹    Don State Technical University, 1, Gagarin sq., Rostov-on-Don, Russian Federation

• ²    University of Novi Sad, 1, Bul. cara Lazara, Novi Sad, Republic of Serbia

Introduction. Essential nonlinearity of the chemical reactions of acids and bases determines the control algorithms in the mode of acidification or alkalization, that is, periodic dosing of a minimum volume of acid or alkali. Such regulation may be ineffective, specifically, it allows insufficient or excessive concentration of the controlled substance. The article discusses the problem of precise regulation of the hydrogen index in mini-bioreactors. It is proposed to use a digital model of the acidity control system to select the concentrations of topped-up solutions, determine the regulation methodology, and improve accuracy. The objective of the work is the assurance of required accuracy of pH regulation in an in vitro mini-model of the gastrointestinal tract of a static type.

Materials and Methods. The initial block diagram of the model included accumulators and flows. It was the base for the main differential equations characterizing the change in volume and acidity. To correct the acidity readings of the resulting solution by temperature, a static model based on the polynomial approximation of experimental data using the least squares method was created. The structural elements of the mathematical model were investigated in the Matlab Simulink application package. To validate the adequacy of the mathematical model, transient characteristics were determined on a real system of in vitro modeling of the artificial gastrointestinal tract of poultry.

Results. Within the framework of this work, the authors created and analyzed a nonlinear mathematical model of pH changes in a bioreactor taking into account external control actions. The flows of hydrochloric acid solution, alkali solution and drain from the reactor were presented as elements of a differential equation describing the accumulation of liquid in the reactor. To improve the accuracy, the solution was modified taking into account the temperature dependence of the hydrogen index. A dosing mathematical model based on a regulator with alkali and acid channels was proposed. The data obtained made it possible to generate a combined model of the pH regulation process in the bioreactor. The adequacy of the solution was confirmed empirically. The models of pH regulator, regulation of the volume of contents in the reactor and chemical reactions were shown in the form of structural diagrams. The transients of a mathematical model and a real control system were compared. It was established that the transient characteristics of the mathematical model and the real system were identical in terms of regulation time. The relative error of regulation of the real system was 0.35 %, and the mathematical model — 0.1 %, which corresponded to the required accuracy of regulation ± 0.1 pH. The influence of the studied flows on the neutralization reaction was shown in the form of graphs. Discussion and Conclusions. The proposed mathematical model will provide selecting optimal methods and algorithms for regulating acidity, which will accelerate the creation of a regulator for the nonlinear process of regulating the hydrogen index. In the future, these developments can be integrated into a comprehensive digital model of the entire artificial gastrointestinal tract of poultry to optimize control algorithms (dosing, mixing, periodicity, etc.), as well as approximation to objects in vivo.

Введение. С начала 1980-х годов исследователи физиологии и функциональных особенностей внутренних органов человека пришли к пониманию, что фокус экспериментов будет смещаться от практик in vivo к in vitro [1]. Актуальность разработки систем аппаратной имитации физиологических процессов обусловлена:

• –    снижением затрат и времени на проведение исследований:

• –    возможностью единовременного проведения однотипных экспериментов;

• –    акцентом на этичность исследований, что предполагает ограничение экспериментов на живых существах.

К началу XXI века сформировалось научное направление по разработке методик и оборудования для моделирования и исследований in vitro [1].

В настоящее время известны статические и динамические in vitro модели желудочно-кишечного тракта (ЖКТ). В первом случае речь идет о моделировании процессов пищеварения при использовании жидких питательных сред [2]. Динамические модели, в отличие от статических, позволяют моделировать перистальтические движения в ЖКТ и используются при работе с пищевыми матрицами в виде суспензий, включающих твердые частицы и волокна.

Цель данной работы — обеспечение требуемой точности регулирования pH в in vitro мини-модели ЖКТ статического типа.

Для достижения цели решаются следующие задачи:

• –    разработка нелинейной математической модели изменения pH в биореакторе с учетом внешних управляющих воздействий;

• –    исследование математической модели методами имитационного моделирования;

• –    доработка математической модели для повышения ее точности путем учета температурной зависимости водородного показателя;

• –    создание математической модели процесса дозирования на основе двухканального конкурентного регулятора (по каналам щелочи и кислоты);

• – разработка объединенной математической модели процесса регулирования pH в биореакторе;

  – проведение экспериментов для подтверждения адекватности объединенной математической модели и определения достигнутой точности регулирования.

Материалы и методы. С точки зрения моделируемого объема модели ЖКТ подразделяются на микро- (до 50 мл), мини- (от 50 до 400 мл) и макросистемы (свыше 400 мл) [3]. Отдельно следует упомянуть микрофлюидные системы [4], но они выходят за рамки данной работы.

Патентный анализ позволяет назвать первое зарегистрированное изобретение в данной сфере — «In vitro модель in vivo пищеварительного тракта»1. Эта динамическая система предшествовала появлению систем типа TIM2 [5]. Идея развивалась в моделях DGM [6], TIM2 [5], HGS [7] и др. Статические модели (DIDGI [8], SIMGI [9], SHIME [10], ARCOL [11] и др.) ушли от сложного моделирования перистальтики и сфокусировались на более точном моделировании собственно процессов пищеварения. Первая причина — техническая сложность и дороговизна реализации систем с динамическим сжатием содержимого. Вторая — развитие методов математического моделирования и микроконтроллерных систем управления, позволивших мониторить среду в пробирке (реакторе) с высокой точностью и стабильностью [4].

В данной работе рассматривается решение частной задачи математического моделирования процесса регулирования pH для in vitro мини-модели желудочно-кишечного тракта (ЖКТ) статического типа [12]. Точность управления кислотностью химуса определяется жесткими требованиями к условиям экспериментов in vitro. Точность автоматического регулирования pH в биореакторе не может быть ниже ±0,1 единицы.2 Это принципиально для правдоподобия условий процессов пищеварения и соблюдения требований к повторяемости результатов опытов. При этом pH может быть от слабощелочной (7,9 pH, ротовая полость) до сильно кислотной (1,3 pH, желудок).

Для моделирования реакции нейтрализации воспользуемся методом накопителей и потоков [13]. Его база — это законы сохранения (накопители), а также математическое описание закономерностей, изменяющих

Информатика, вычислительная техника и управление

количество накапливаемого признака (потоки). Структурная схема данной модели с двумя накопителями представлена на рис. 1.

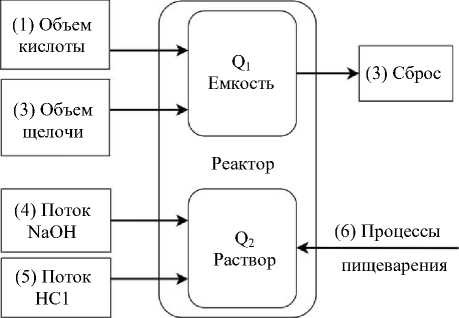
Рис. 1. Структурная схема модели с двумя накопителями

Реактор как физический объект накапливает некоторое количество:

– жидкости ( Q 1 );

– ионов водорода ( Q 2 ).

В этой емкости идет контролируемый процесс пищеварения с изменением pH и объема жидкости.

На первый накопитель действуют три потока:

• –    1-й — объем доливаемой кислоты;

• –    2-й — объем доливаемой щелочи;

• –    3-й — объем, выливаемый из реактора.

На второй накопитель также влияют три потока:

• –    4-й — подача насосом гидроксида натрия [2];

• –    5-й — поступление соляной кислоты [2];

• –    6-й — изменение pH в процессе пищеварения.

Последний поток представляет собой возмущающее воздействие и не исследуется в данной работе.

Результаты исследования. Рассмотрим математическую реализацию модели для описания химических процессов.

Объем жидкости в реакторе:

физико-

V = S • h.

Изменение объема жидкости в реакторе:

dV = S • dh .

Для удобства назовем:

• –    поток раствора соляной кислоты — q ₁ = G ₁;

• –    поток раствора щелочи (гидроксид натрия) — q ₂ = G ₂;

• – поток слива раствора из реактора — q ₂ = G ₃.

Таким образом, дифференциальное уравнение, описывающее накопление жидкости в реакторе:

v = V • C, где V — это объем вещества, л; C — молярная концентрация, моль/л. Из (4) и (1) получаем:

dV = d (S • h • C ) = S •[ C • dh+h • dC I. dt dt               I dt      dt)

На изменение концентрации раствора влияют потоки щелочи и кислоты с определенной концентрацией. Значит:

S •( C• dh + h• — ) = ( G • C_NaOH-G^ • C_HCl ).

( dt       dt ) ^{v 1 NaOH 2 HCl}’

Из (6) выведем изменение концентрации и упростим выражение:

~7~ =   , ( ^G 1 ^{( C} NaOH — ^C ) ^{+ G} 2 ^{( C} - ^C HCl ) ) .

dt S • h

Представим систему дифференциальных уравнений, описывающих динамику изменения объема и концентрации раствора в биореакторе:

dh

' dC

. dt

= 1( G 1 + G 2 - G 3 ),

' = ini ( G 1 ( C NaOH - C ) + G 2 ( C - Ch_Q ) ) .

Зная основы химии и принимая во внимание (8), можно определить концентрацию катионов H ([ H ⁺]). Концентрации ионов водорода ([ H ⁺]) и гидроксид-ионов ([ OH ^-]) в дистиллированной воде при 25 °C равны и составляют по 10^-7 моль/л. Это следует из определения ионного произведения воды [11]:

K = [ H ⁺] ^х [ OH "] = 10 ^{- 14}mol²/ I ² ( at 25 ° C ) .

Также стоит учитывать, что:

T = [ OH ^- ] - [ H ⁺ ] = [ Na ⁺ ] - [ Cl ^- ].

Теперь найдем [ H ⁺] (обозначим, как C_H ) через квадратный корень из предыдущих выражений с учетом концентрации раствора по уравнению (4) [14]:

T н = 2

1 + —r-1 , T >  0, у 2        '        '

<

Ch =

T ( [

=J1

^H 2 V

K , T = 0,

1 + —г+1 , T < 0. гр 2         J

T

Здесь ионы i = 4.

Для создания системы регулирования с обратной показателя (pH) используем отрицательный десятичный связью по кислотности в виде водородного логарифм из концентрации, рассчитанной по

уравнениям (7), и получим кислотность раствора при нормальных условиях, то есть при 25 °C.

Однако содержимое биореактора не всегда находится в нормальных условиях. Например, для создания искусственной среды, свойственной in vivo среде желудочно-кишечного тракта домашней птицы, в реакторе поддерживается температура 42 °C. Поэтому на высокоточных измерителях pH получили матрицу изменения pH буферных растворов в зависимости от температуры. Показания фиксировали по измерительной системе с термокомпенсацией для применяемого электрода [13]. С этой целью использовали данные эксперимента и сведения из открытых источников3.

В итоге построили статическую модель. Ее получили полиномиальной аппроксимацией методом наименьших квадратов. Зависимость pH от температуры визуализирована на рис. 2 [14–16].

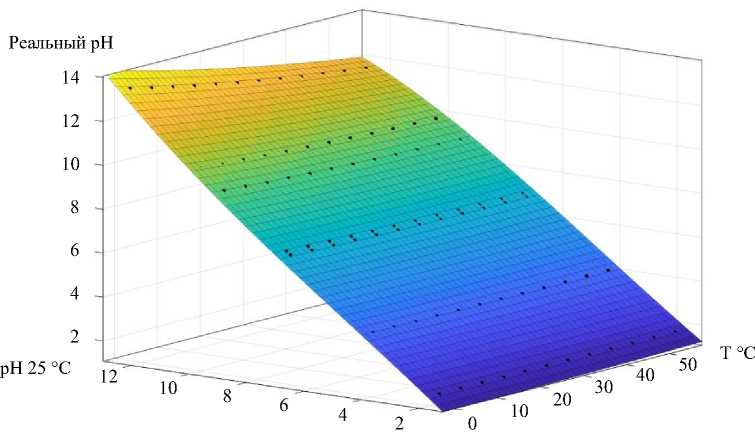
Рис. 2. Поверхность, описывающая зависимость pH от температуры (12)

Информатика, вычислительная техника и управление

F ( x ) = p 00 + p 10 • x + p 01 - y + p 20 • x ² + p 1L x • y + p 02 • y ² + + p 30 • x ³ + p 21 - x ² • y + p 12 • x • y².

Коэффициенты уравнения представлены в таблице 1.

Таблица 1

Коэффициенты уравнения (11)

Коэффициент	Значение
p 00	0,154
p 10	–0,00511
p 01	0,899
p 20	–2,998 ∙ 10–6
p 11	0,00333
p 02	0,0130
p 30	-3,226 • 10-7
p 21	1,588 • 10-5
p 12	-4,8 • 10-4

Для определения переходных процессов в системе построим математическую модель в прикладном пакете Matlab Simulink (рис. 3):

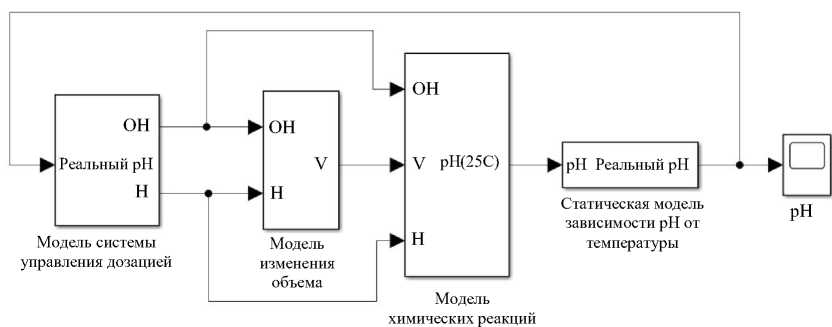
Рис. 3. Общая структура математической модели в Matlab Simulink

Рассмотрим созданную систему по блокам. Первый — блок двухканального регулятора по кислотности с обратной связью. В цепь обратной связи введены шумы для моделирования случайных событий реальной системы измерения кислотности и погрешности измерительных приборов.

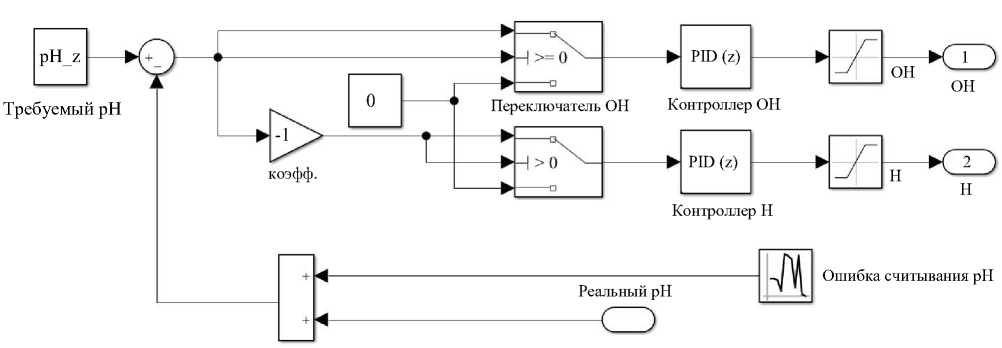
Рис. 4. Структура регулятора pH, блок «Модель системы управления дозацией »

Второй блок — это система контроля объема раствора в реакторе. Функция Volume change model моделирует включение откачивания. Так обеспечивается постепенный сброс раствора до необходимого объема при его приближении к максимуму.

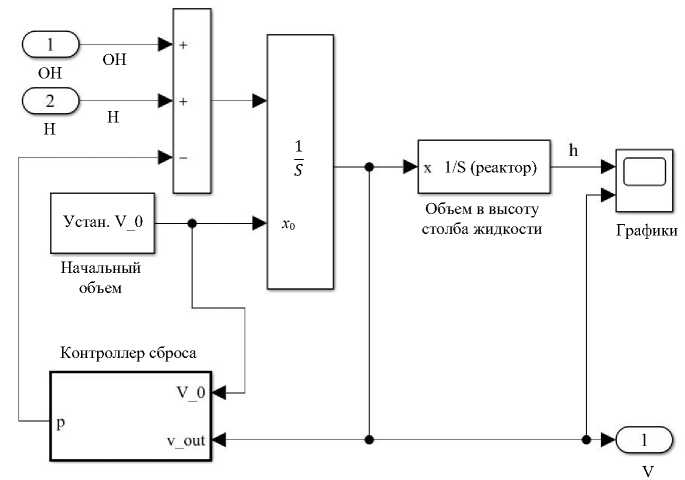
Рис. 5. Структура модели регулирования объема содержимого в реакторе, блок «Модель изменения объема»

Третий блок — основной. Он реализует расчет химической реакции кислоты и щелочи при добавлении в реактор и вычисление pH конечного раствора при нормальных условиях. Функция Neutralization определяет концентрацию ионов водорода в растворе [12]. Блок Concentration in pH преобразует концентрацию в водородный показатель pH.

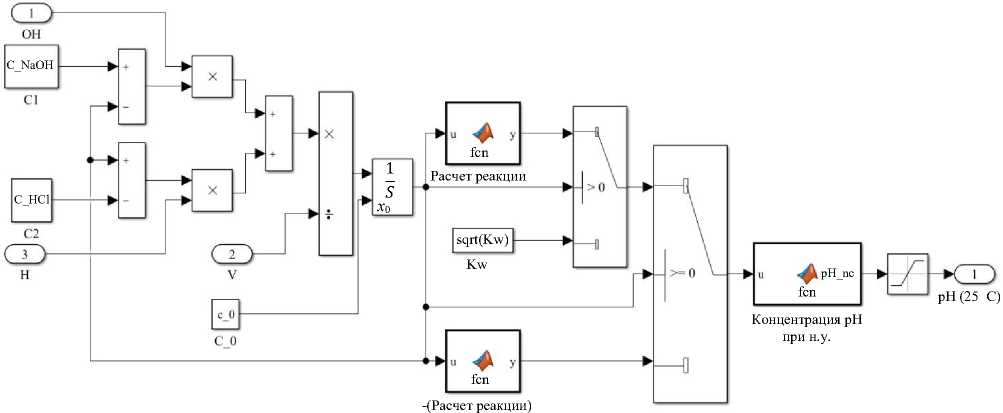
Рис. 6. Структура модели, описывающей химические реакции, блок «Модель химических реакций»

Функция статистической модели в четвертом блоке (Temperature correction) позволяет учесть температурные

изменения раствора.

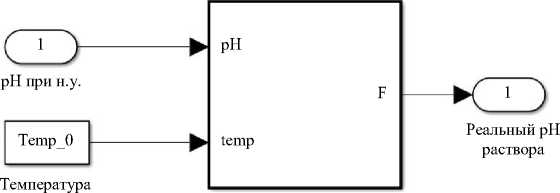
раствора

Температурная коррекция водородного показателя

Рис. 7. Структура модели, описывающей изменение кислотности от температуры, блок «Статическая модель зависимости pH от температуры»

Информатика, вычислительная техника и управление

Для определения адекватности переходных характеристик результирующей математической модели проводились эксперименты на имитационной модели. Реальная модель представлена системой автоматизированного управления искусственным ЖКТ домашней птицы с одним блоком управления и биореактором. Оборудование представлено на рис. 8.

а )

б )

Рис. 8. Оборудование для проведения исследований: а — система управления параметрами среды в биореакторе; б — элементы биореактора. 1 — управляемые перемешивающие устройства; 2 — нагреватели;

3 — порты для датчиков и системы дозации жидкостей

Опишем методику проведения эксперимента. В математической модели учитываются характеристики реальной системы:

– заданная кислотность;

– параметры реактора (площадь основания и высота);

– концентрации доливаемых веществ (кислоты и щелочи);

– начальная концентрация раствора;

– начальный объем раствора;

– температура раствора на протяжении всего эксперимента;

– дискретность процесса регулирования [14].

Математическая модель представляет собой идеальную систему: смешивание растворов в реакторе происходит мгновенно и равномерно. В реальных условиях это невозможно, поэтому для равномерного растворения добавленной кислоты или щелочи необходимо принудительное перемешивание. В имитационной модели данная проблема решается магнитной мешалкой с управлением SCADA4.

К сожалению, такой тип перемешивающего устройства наводит на pH-электрод электромагнитные помехи. Для исключения помех устройство перемешивания кратковременно отключалось. Дискретность измерений и работы регулятора составила 20 секунд, что обусловлено экспериментально установленным временем нормализации показаний pH электрода в реакторе (по документации электрода возможна дискретизация до 1– 2 минут) 5, 6. В целях обеспечения безопасности регулятор реальной системы ограничен в максимальном объеме дозируемой кислоты или щелочи, что учитывалось в модели.

На рис. 9 сравниваются переходный процесс математической модели и реальной системы управления. PH-электрод — это чувствительный элемент, на который воздействуют внешние электромагнитные помехи.

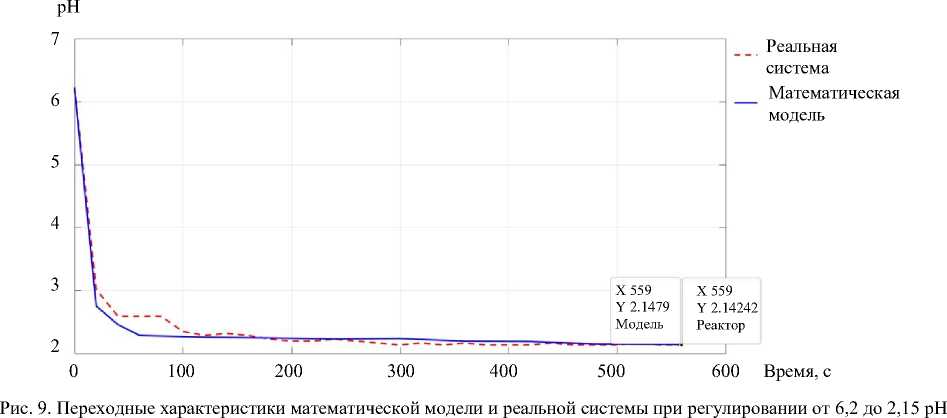
Один из экспериментов проводился при заданной кислотности раствора 2,15±0,05 pH. Кислотность исходного раствора — 6,2 pH. Температура раствора в реакторе — 22,25 °C. Для изменения кислотности использовались растворы 0,1 моль/литр NaOH и 0,1 моль/литр HCl . Алгоритм дозации заключался в дискретном пропорциональном регулировании.

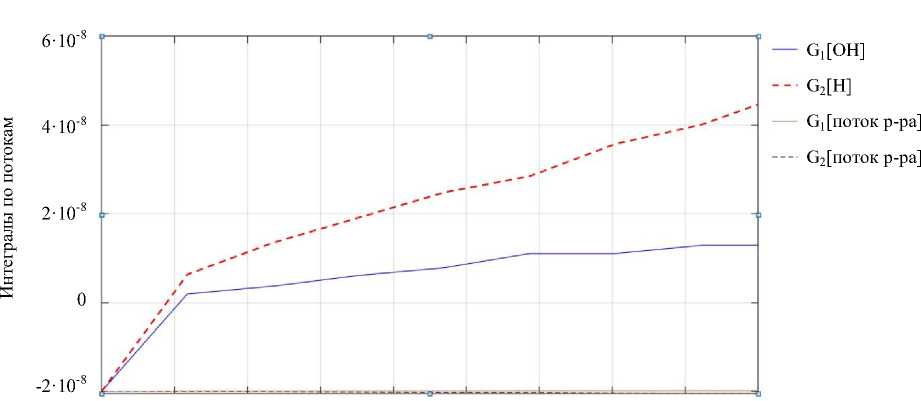
На рис. 10 представлены интегралы по потокам из дифференциального уравнения (7).

0       50      100     150     200    250     300     350     400     450 Время, c

Рис. 10. Влияние каждого потока на реакцию нейтрализации в ходе экспериментов

Обсуждение и заключения. Анализ результатов моделирования показал, что потоки с концентрацией раствора в реакторе не вносят весомого вклада в регулирование всей системы, поэтому ими можно пренебречь. Тогда система дифференциальных уравнений цифровой модели (8) приобретет следующий вид:

dC

— =1 G + G2 -G), dt S ( 1     2     3)

. dt

= S - h ( G ¹ ■ C NaOH

G 2 ■ C HCl ) .

По результатам экспериментов с учетом концентрации раствора в реакторе относительная погрешность установившейся кислотности раствора для математической модели составила 0,1 %, а для реальной системы с тем же алгоритмом — 0,35 %.

Итак, в математической модели учтем погрешность показаний электрода и пренебрежем перемешиванием растворов. Абсолютная погрешность результатов регулирования находится в допустимых пределах и не превышает ±0,1 pH от заданной величины. Это означает, что разработанная математическая модель адекватно описывает кривую реакции нейтрализации и в будущем позволит подобрать оптимальные алгоритмы регулирования, что было бы трудоемким процессом в реальной системе.

Информатика, вычислительная техника и управление

Разработанная модель решает поставленную задачу. Она представляет собой математический инструмент для создания методик и алгоритмов регулирования pH с учетом температуры содержимого мини-реактора, начальной концентрации основного раствора и концентраций доливаемых растворов. Такой подход позволяет совершенствовать существующие алгоритмы управления.