Математическая модель состояния объектов молниезащиты с учетом рельефа местности

Исследования американских ученых, опубликованные в ноябрьском 2014 г. журнале Science, показывают, что глобальное потепление значительно увеличивает частоту ударов молний. По данным Калифорнийского университета в Беркли, на каждые два удара молнии в 2000 г. придется три удара в 2100-м. Большее число ударов молний сопровождается большим количеством пострадавших людей, вплоть до смертельных исходов.

Средством борьбы с поражением молний объектов инфраструктуры является молниеотвод. Эффективность работы молниеотводов зависит от грамотного их размещения. Оптимизировать размещение средств молниезащиты можно на основе имитационного моделирования процесса протекания разряда молнии и поражения ими объектов инфраструктуры. Одна из таких моделей представлена в работе [1]. Она на основе статистической модели распространения молнии позволяет проводить моделирование стержневой молниезащиты объектов. Модель дает распределения напряженности электростатического поля на объектах молниезащиты и вероятности их поражения молнией с учетом конфигурации защищаемых объектов. В точках с наибольшим значением наводимой напряженности электростатического поля и вероятности поражения объектов молнией рекомендуют устанавливать стержневые мониеотводы.

На развитие кучево-дождевой облачности – источника молний оказывает влияние рельеф местности. Следует ожидать, что на распределение наводимой напряженности электростатического поля на объектах молниезащиты и на вероятности их поражения молнией также будет влиять рельеф местности. Поэтому имитационные модели состояния объектов молниезащиты должны учитывать как особенности конфигурации объектов молниезащиты, так и особенности рельефа местности, на которой расположены эти объекты.

Целью исследования стала разработка численной модели расчета напряженности электростатического поля и вероятности поражения объектов защиты с учетом рельефа местности.

В настоящей статье решаются следующие задачи:

• •    разрабатывается математическая модель состояния объектов молниезащины с учетом рельефа местности;

• •    производится расчет распределений напряженности электростатического поля и вероятности поражения объектов молниезащиты с учетом рельефа местности.

Математическая модель состояния объектов молниезащиты с учетом рельефа местности

В математической модели объекты защиты и рельеф местности представляются в виде полигонов, которые разбиваются на точки (узлы сетки). Пример простейшего объекта, ангар, изображен на рис. 1.

Каждый узел представляется в виде сферы с зарядом, наводимым внешним полем с некоторой напряжённостью E_o , созданной кучево-дождевой облачностью с грозовыми явлениями, и радиусом, равным половине шага регулярной сетки d . Для полученной системы сфер c центрами в точках (x i , y, z) (i=1,^, n) вычисляют значения зарядов q i , используя закон Кулона, принцип суперпозиции и зеркального отражения зарядов, в предположении, что сферы заземлены и имеют нулевой потенциал:

1 1 q1+ 1 1 q2+...+ 1 1 4πε0E0z1, d 2z1+d a12 b12 a1n b1n qn= 1 1 q1+ 1 1 q2+...+ 1 1 4πε0E0z2, a21 b21 d 2z2+d a2n b2n qn= (1) . 1 1 q1+ 1 1 q2+...+ 1 1 4πε0E0zn, an1 bn1 an2 bn2 d 2z n+d qn= где £0- диэлектрическая проницаемость воздуха, xm, ym, zm - координаты центра m-й сферы; Хп, Уп, Zn - координаты центра п-й сферы; а„„ = (^ Xn + (Ут Уп)2 + (Zm ZJ2 - расстояние между центрами m-Й и п-Й сфер; bmn = V (xm Xn )2 +(ym Уп У +(Zm + Zn ^2 - расстояние между центрами m-й сферы и зеркального отражения n-й сферы.

a)

b)

Рис. 1. Полигональная модель ангара ( a ) и ее дискретизация ( b )

По значениям заряда q_i рассчитывается напряжённость E_i для каждой заряженной сферы:

= q i           q i      + у q j

4 ⁿ E 0d²  4^0 ( d + ² z i ) ²  j = i4Tteo^Ri

+ N	qj 2	i1 ∑ qj 2	∑ n	q j
j = i + 1	4πε 0 R i2j	j = 1 4 nE0R0ii	j = i + 1	4πε0R0 2 ij

где

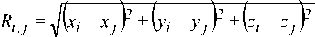
расстояние между центрами i -й и j -й сфер;

R _0i,j = (ХУ x j₀ У + ( y i y joУ + ( z i z joУ — расстояние между центрами i -й сферы и зеркального отражения j -й сферы.

По значению напряжённости электростатического поля в каждом узле получаем распределение напряжённости на защищаемом объекте.

Распределение напряжённости электростатического поля является основным входным параметром для расчёта траектории молниевого разряда, движущегося в сторону точки с наибольшим значением напряжённости. При этом лидер молнии испытывает постоянные возмущения в виде неоднородности электрического сопротивления воздуха, в результате чего молниевый разряд представляется в виде системы ломаных. Для воспроизведения этих ломаных в модели развития молнии используется две системы координат: глобальная и локальная. Глобальная система координат (X,Y,Z) неподвижна. Начало отсчета совпадает с началом молнии. Поверхность Земли сдвинута на расстояние H , т. е. (X, Y, Z + H) . Локальная система координат (x′, y′,z′) перемещается вместе с молнией. Начало отсчета там, где находится лидер. Направление оси х′ выбирается так, чтобы она совпадала с направлением последней ступени лидера молнии. Электрическое поле молнии на много порядков превышает суммарное поле всего остального, стримеры, окружающие лидер, как бы «нащупывают» направление движения на некотором расстоянии от лидера L op , а само поле молнии можно считать «источником» хаоса, которое и приводит к случайному характеру последующего продвижения лидера. Расстояние L_op не превышает размеров стримерной зоны, которая определяется длиной стримеров l ст р , и зависит от линейной плотности объемного заряда τ в соответствии с соотношением [1]

τ lстр 4πε0 Eстр ,

где Е_стр – средняя напряженность электрического поля в стримерной зоне.

В локальной системе координат направление перемещения лидера по углу φ (рис. 2) подчиняется равномерному распределению на интервале [0; π], а по углу α относительно оси x′ – нормальному закону распределения со среднеквадратичным отклонением σ θ =0.2÷0.3 и больше (в зависимости от длины и мощности молнии) относительно нулевого среднего значения [1]:

fnorm

(α) =

2π σθ

exp

α2

2σ_θ² .

Длина L отрезка молнии, «выросшей» по следу стримера, является случайной величиной с логнормальным законом распределения [2]:

lognorm

(L) =

2π σp

L exp

( ln ( L/L 0 )) ²

2 σ_p ²

Величины L и τ выбирают из диапазона величин наблюдаемых в природе. Знак заряда выбираются случайно, исходя из условия, что 90 % молний имеют отрицательный заряд.

В общем виде определяется направление S при заданном максимальном значении направляющего вектора E и угле раскрытия α [2]:

S = E + d 1 , (6)

где d 1 – случайно отклоняющий вектор, определяемый через вектор d₀ , лежащий в плоскости, перпендикулярной вектору E .

Для разряда молнии необходимо наличие как облачного, так и встречного лидера (стримера), характеризующего электрофизические процессы на поверхности земли и на объектах молниезащиты.

Модель формирования стримера схожа с моделью возникновения и развития облачного лидера молнии. Объясняется это тем, что зарождение и развитие стримера происходит практически в той же среде и в тех же условиях, что и облачного лидера. Отличительная особенность – электрофизические процессы на объектах защиты. Рассмотрим их.

Наличие достаточной ионизации воздуха вокруг объектов защиты служит одним из условий появления стримера от этих объектов. Это наблюдается, когда средняя напряженность электрического поля в пространстве между облаком и точкой начала зарождения стримера на объекте защиты не меньше средней напряженности поля в канале лидера ( Е≥Е_кр=3·10⁶ В/м²). Развитие стримера будет наблюдаться при условии, когда электрическое поле в головке стримера достаточно для удлинения стримера на такое расстояние, при котором усиление поля будет достаточным для дальнейшего продвижения стримера и лидера молнии.

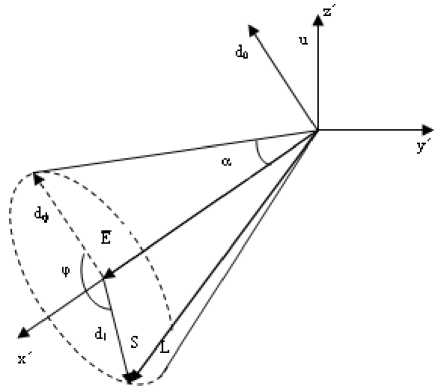
Рис. 2. Формирование ступени лидера

Моделирование указанных условий производится на основе коррекции q_i и Е_i с учетом зон ионизации (7), стримерной зоны (8) и проверки скорректированных значений Е i с критическим s sss

Е кр . При выполнении условия Е>Е_кр, принимается решение, что ионное облако растет и есть условия для зарождения и развития стримера в узле объекта защиты, в противном случае зарождения и развития нет [2].

R и.зi

q _i

4πε0E1i ,

R= q c.з   4πε0E2iR0 ,

где R_и.з.i – радиус зоны ионизации воздуха вокруг i -го узла; E_1i – электрическая прочность воздуха; R с.з.i – радиус стримерной зоны i -го узла; E 2i – напряженность электрического поля в стри- ..

мерной зоне i -го узла; R₀ – радиус ионного облака.

Моделирование процесса дальнейшего развития стримера производится на основе расчета: скорости роста ионного облака V в условиях внешнего электрического поля E₀ (9); увеличения первоначального радиуса ионного облака ∆R (10); радиуса сферы, образованного объемным электрическим зарядом ионного облака R_cо (11). В качестве радиуса ионного облака ..

используется К_{и о}, если R_UOC3 . , в противном случае - R_c . ₃ . .

V = μE _ф ,

ΔR = μE ф Δ t ,

R с.o. = r 0 + ΔR ,

где μ – подвижность ионов; ∆t – время действия поля.

Следующим этапом моделирования является проверка выполнения условия рождения лидера внутри ионного облака. Для преодоления ионного облака необходимо, чтобы напряжение внутри облака было больше 0,6^R со , а в узле - больше (12):

3   ∆ U _m ⁴ _in µ ∆ t

²      2R с ². з .     ^,

где ∆U _min – минимальное напряжение стримерной зоны, при которой лидер прекращает свое существование.

При выполнении указанных условий формируется первая ступень стримера. Формирование траектории движения встречного лидера осуществлялся по аналогии с формированием траектории движения облачного лидера.

Для моделирования процесса формирования последующих ступеней встречного лидера ss рассчитывается скорость роста встречного лидера Vл (13), время действия внешнего электрического поля и переносимый за это время заряд (14) и ток лидера (15):

vл = a Vv ,

Q =

ⁱ Т ^R с.з.

V,

л

i

2ns 0 a A U331

hf^

к E 0 J где а – константа, равная 15 м/с B ; ∆Uг – превышение потенциала головки лидера над потенциалом внешнего поля; Ест – поле в стримерной зоне при нормальных условиях.

На основе полученных результатов определяется линейная плотность электрического заряда τ (16) и длина L (17) ступени лидера:

T = ^ , ^R с . з .

L = VлA t.

Эти данные используются для определения координат точки на границе стримерной зоны,

_ts__ необходимой для задания направления формирования ступени встречного лидера.

Результаты численного моделирования лидера и стримера на объекте молниезащиты, расчетов распределений напряженности электростатического поля и вероятности поражения объектов молниезащиты с учетом рельефа местности

Результаты численного моделирования облачного лидера и стримера на объектах молние-защиты представлены на рис. 3.

Используя описанную математическую модель грозового разряда и введя в нее произвольный рельеф местности, получили расчётное распределение наводимой напряжённости электростатического поля (рис. 4). Распределение не противоречит реальной действительности.

На основе выборки, состоящей из 1500 случаев численного эксперимента поражения объектов молниезащиты с учетом рельефа местности, получено расчетное распределение вероятности поражения объектов защиты (рис. 5). Анализ результатов показывает, что чем выше рельеф местности, тем выше вероятность попадания в эту местность молниевого разряда. Полученные результаты не противоречат реальной действительности. Распределения вероятно-

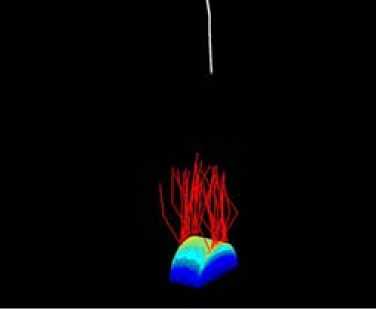
Рис. 3. Пример численного моделирования лидера и стримера на объекте молниезащиты

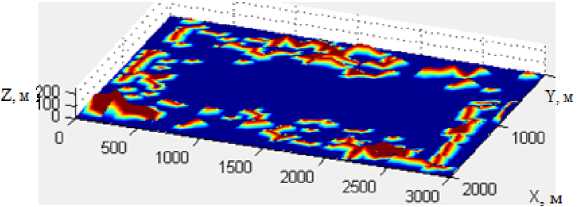
Рис. 4. Распределение напряжённости с учетом рельефа местности

Рис. 5. Распределения вероятности поражения объектов молниезащиты стей поражения объектов молниезащиты, расчитанные для конкретных местностей, позволят повысить эффективность молниезащиты.

Выводы

Предложена математическая модель состояния объектов молниезащиты с учетом рельефа местности. Она позволяет оптимизировать размещение средств пассивной молниезащиты объектов, а для средств активной молниезащиты – определить момент их активации и оценить эффективность их функционирования.