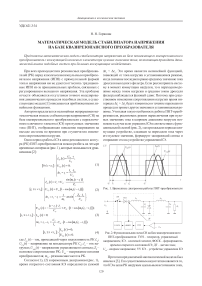
Математическая модель стабилизатора напряжения на базе квазирезонансного преобразователя

При всех преимуществах резонансных преобразователей (РК) перед классическим импульсным преобразователем напряжения (ИПН) с прямоугольной формой тока и напряжения им не удается оттеснить традиционные ИПН из-за принципиальных проблем, связанных с регулированием выходного напряжения. Эта проблема отчасти объясняется отсутствием точного моделирования динамических процессов подобных систем, а существующие модели [1] описываются приближенными линейными функциями.

Автором предлагается нелинейная непрерывная математическая модель стабилизатора напряжения (СН) на базе квазирезонансного преобразователя с переключением ключевого элемента (КЭ) при нулевых значениях тока (ПНТ), отображающая поведение напряжения на выходе системы во времени при ступенчатом измене

нии сопротивления нагрузки.

Один период работы КЭ в цепи резонансного контура (РК) ПНТ-преобразователя можно разбить на четыре временных интервала (рис. 1), которые описываются уравнениями [2]:

A t _j + A 1 ₂ . Это время является нелинейной функцией, зависящей от тока нагрузки в установившемся режиме, когда значение последнего равно среднему значению тока дросселя выходного фильтра. Если рассматривать систему в момент коммутации нагрузки, то в переходном режиме между током нагрузки и средним током дросселя фильтра наблюдается фазовый сдвиг Поэтому при существенном изменении сопротивления нагрузки время интервала A t _j + A 1 ₂ будет изменяться в течение переходного процесса и примет другое значение в установившемся режиме. Учитывая такую особенность работы ПНТ-преобразователя, реализовать режим переключения при нулевых значениях тока в широком диапазоне нагрузок возможно в случае если управлять КЭ в соответствии с функциональной схемой (рис. 2), где при каждом периоде коммутации устройство, следящее за переходом тока через его нулевое значение, формирует запирающий сигнал и отправляет его на устройство управления КЭ.

[ 0 <  t <  t , ] :

[ t , <  t <  t 2 ] :

^[ t 2 <  t <  t з ^] :

U„ • t I L, ( t ) = ;

L p

U c , ( t ) - 0;

a t = t = I^ . ¹¹   и „

sin ( ® 0 ( t ^- 1 , ) )

i_l Д t ) - Д + u„ • L p           n ЬЛ

Z 0         ;

U C p ⁽ t )^{- U} «x ( 1 - cos ( ® 0 ⁽ t - t i ) )) ;

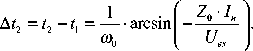
( t — 1 2 ) • I »

U Cp ( t ) ^--- Д-----⁺ U .X '( 1 - cos ( ® 0 ( t 2 - t i ))) ;

^c p

I l , ( t ) - 0;                                             (3)

C

^A t 3 - t 3 ^- t 2 ^-—• U „ '( 1 ^- cos ( ® 0 ⁽ t 2 ^- t i ) )) .

I H

[ 1 3 <  t <  1 4 ] :

<

I l , ( t ) - 0;

. U_{c p} ( t ) - 0.

где I ( t ) - ток, проходящий через индуктивность РК L _p ; U ( t ) - напряжение на конденсаторе РК С _р ; I _я - ток нагрузки; U _упр ( t ) - напряжение управляющего сигнала; Z ₀ -волновое сопротивление РК; U _дх - напряжение питания преобразователя; ю ₀ - резонансная частота РК.

Согласно (1), (2) и временным диаграммам (рис. 1), время открытого состояния КЭ определяется суммой

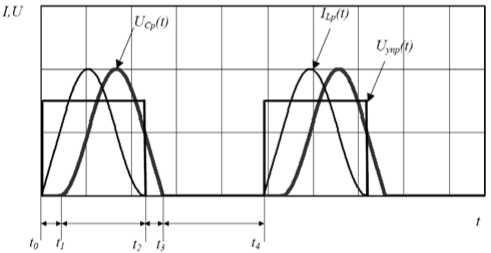
Рис. 1. Временные диаграммы работы ПНТ-преобразователя

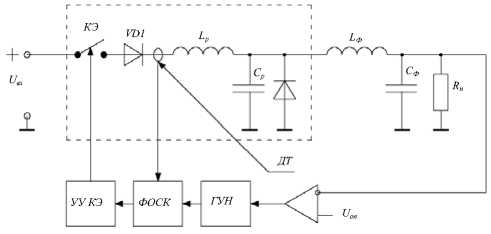
Рис. 2. Функциональная схема СН на базе квазирезонансного ПНТ-преобразователя: ГУН - генератор, управляемый напряжением; КЭ - ключевой элемент, ФОСК - формирователь времени открытого состояния КЭ; ДТ - датчик тока;

U - опорное напряжение; УУ КЭ - устройство управления КЭ

Прототип предлагаемой математической модели был описан в [3]. Его существенным недостатком является то, что КЭ в цепи РК нагружен идеальным источником тока,

а такая модель не учитывает особенности работы выходного L _ф С ф -фильтра преобразователя, который в свою очередь принимает участие в резонансном цикле. В связи с этим для исключения срыва резонансного процесса индуктивность дросселя фильтра рассчитывается таким образом, чтобы обеспечить в нем режим непрерывного изменения тока. Поэтому на значение индуктивности дросселя накладывается обязательное ограничение: L _ф >>L_p (примерно на порядок). Учитывая тот факт, что напряжение на резонансной емкости имеет фазовый сдвиг по отношению к току I ( t ) (запаздывание) в соответствие с режимом ПНТ, то инерционностью устройства слежения за режимом ПНТ можно пренебречь.

На основании вышеизложенного можно сделать вывод, что на время открытого состояния КЭ влияет не только среднее значение тока дросселя выходного фильтра, но и наложенное на него периодическое изменение тока -пульсация. На этом основании постановка задачи моделирования сводится к определению влияния пульсаций тока дросселя выходного фильтра на временные режимы работы КЭ в течение одного периода коммутации, а значит, и на динамику системы в целом.

Для дальнейшего анализа считаем, что полуволна тока за время A 1 ₁ + A 1 ₂ (см. рис. 1) имеет синусоидальную форму. Тогда форма тока через L _p будет выглядеть так, как показано на рис. 3. Регулирование выходного напряжения осуществляется посредством частотно-импульсной модуляции (ЧИМ) за счет изменения среднего значения напряжения на конденсаторе РК в зависимости от текущей частоты коммутации, при условии, что собственная частота РК больше максимальной частоты коммутации.

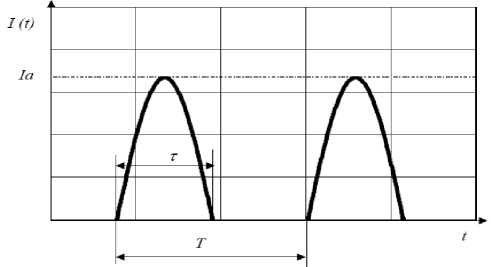
Рис. 3. Идеализированная временная диаграмма тока индуктивности резонансного контура ПНТ-преобразователя: I _a - амплитудное значение тока; t - длительность импульса соответствующая времени открытого состояния КЭ;

Т- период коммутации

Так как запасаемая энергия в индуктивности РК опре деляется током нагрузки, то зависимость длины импуль са от среднего тока дросселя выходного фильтра можно вывести через эффективное значение тока Iэф [4] индуктивности РКL :

р

<

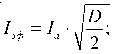
D = - .

T

Подставляя известную для нахождения амплитудного значения тока формулу I=I _эф + U _aJ Z ₀ в (5), получим

D =

I эф

U

I, + ^эф у

Z 0

■ 2

Учитывая, что искомое выражение должно определять зависимость относительной длины импульса тока индуктивности РК от периодического изменения тока дросселя выходного фильтра за один период коммутации, его можно записать следующим образом:

-12

A D ( I^ ) =

<

I..K ( I /J

L ф П Ьф

I,,K ( I. ,) + —

L ф П Ьф ' гу Z ₀

■ 2;

A I

K ( I ) = _LA .

П\ Ьф

1Lф где AILф - размах пульсаций тока дросселя выходного фильтра; ILф - среднее значение тока дросселя выходного фильтра.

На основании параметрической нелинейности (7), обусловленной нелинейной зависимостью коэффициента передачи ПНТ-преобразователя от тока нагрузи К ( I _L ф ) [3], и модели выходного LC- фильтра [5] была синтезирована математическая модель СН на базе квазирезонансного ПНТ-преобразователя (рис. 4).

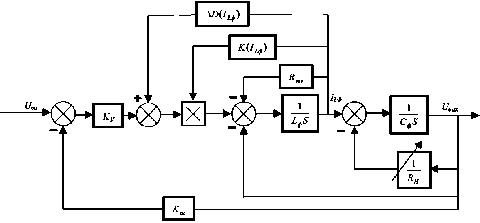
Рис. 4. Структурная схема непрерывной нелинейной модели СН на базе понижающего квазирезонансного

ПНТ-преобразователя: U _зп - опорное напряжение, R _зкв - сопротивление, эквивалентное активному внутреннему сопротивлению ПНТ-преобразователя; К _{о =} - коэффициент обратной связи; К _у - коэффициент усиления

Временные диаграммы процессов в силовой цепи СН без дополнительной коррекции, полученные в результате моделирования с использованием синтезированной нелинейной непрерывной модели и имитационного моделирования в пакете Micro-Cap 7.0, приведены на рис. 5. В этом пакете были рассчитаны все функциональные узлы ПНТ-преобразователя (см. рис. 2), при реализации которых были применены известные схемотехнические решения, а также учтены все динамические свойства реальных элементов. Это позволяет дать адекватную оценку точности синтезированной модели.

На основании проведенных исследований и полученных результатов можно сделать следующие выводы:

• -    адекватность полученной модели подтверждается при исследовании электромагнитных процессов на ЭВМ с использованием имитационной модели в формате P-Spice, справедливость которой обосновывается результатами физических экспериментов [6];

• -    полученную модель можно применять для анализа динамических качеств СН, построенного на базе ПНТ-преобразователя, а также использовать как основной элемент методики синтеза закона управления, на основе известных методов исследования нелинейных систем;

• -    на основании выявленных параметрических связей и взаимовлияний энергетических режимов силовых цепей СН и его динамических свойств, можно выработать оптимальный режим работы системы путем совместного решения энергетической и динамической подзадач.